输出频率对IGBT元件结温波动的影响

丁杰，唐玉兔，忻力，胡昌发

（南车株洲电力机车研究所有限公司南车电气技术与材料工程研究院，湖南株洲 412001）

输出频率对IGBT元件结温波动的影响

丁杰，唐玉兔，忻力，胡昌发

（南车株洲电力机车研究所有限公司南车电气技术与材料工程研究院，湖南株洲 412001）

为分析输出频率对结温波动的影响，开发了基于模型降阶方法的程序，运用该程序对IGBT元件的热模型进行了计算，将得到的温度计算结果与ANSYS稳态计算结果进行比较，结果的一致性证明该方法是有效的。在此基础上，利用该程序计算得到了不同输出频率下IGBT元件的结温波动曲线。通过瞬态温度与基于平均损耗计算的稳定温度对比可知：1 Hz输出频率时半正弦波损耗产生的温度波动范围为-7.2%～7.6%，方波损耗产生的温度波动范围为-3.9%～6.5%，输出频率对温度波动的影响显著；50 Hz输出频率时对温度波动的影响较小，可以忽略；半正弦波损耗产生的温度波动大于方波损耗。分析结果可为IGBT元件瞬态温度计算提供参考，基于模型降阶的程序可以进一步运用于其他电力电子器件瞬态温度的计算。

绝缘栅双极晶体管；输出频率；结温波动；模型降阶

1 引言

在大量的工程应用中，为了简化计算，通常都是基于一个调制周期内的平均值来对IGBT元件的损耗和结温进行分析，因此，输出频率的改变不会影响平均损耗和结温的计算值。实际上，IGBT元件的损耗是随负载电流的大小而变化，输出频率较高时产生的结温波动较小，输出频率较低时的结温波动会变大。结温的波动会产生交变的热应力，从而对IGBT元件的热循环次数、可靠性及使用寿命产生一定的影响。

由于IGBT元件结构复杂、散热条件多样，采用有限元法或有限体积法需要解算很大规模的矩阵方程，导致稳态问题的计算尚需要大量的时间，瞬态问题则需要更为漫长的计算时间和庞大的计算机资源。因此，实际应用与文献中较少涉及IGBT元件瞬态温度的计算。

为提高计算速度并保证计算精度，开发了基于模型降阶方法［1-7］的程序，对不同输出频率下的IGBT元件结温波动进行了快速计算，分析了芯片最高温度的变化特点和波动情况。分析结果与开发程序可为电力电子器件瞬态温度计算提供参考。

2 模型降阶方法

图1示出了基于Matlab软件、ANSYS软件和Krylov子空间投影法缩聚自由度进行模型降阶并快速计算的程序流程。

图1 模型降阶程序流程Fig.1 Program flow chart of model order reduction

首先通过CFD模型得到对流换热系数分布，为ANSYS热传导有限元模型提供准确的边界条件［7］。模型中有m个热源的损耗需要改变时，分别建立损耗均为0、第1个热源为单位损耗、第2个热源为单位损耗、…、第m个热源为单位损耗的（m+1）个ANSYS有限元模型，再从这些文件中分别提取热传导矩阵和热容矩阵，并保存为文件（Cond_File0.dat，Cap_File0.dat，Cond_File1.dat，Cap_File1.dat，Cond_File2.dat，Cap_File2.dat，…，Cond_Filem.dat，Cap_Filem.dat）。

在Matlab软件中利用读取文件命令，可以从Cond_File0.dat文件整理得到新的热传导矩阵Conductance0（n×n）、载荷列阵 LoadVector0（n×1），从 Cap_File0.dat文件得到热容矩阵 Capci-tance0（n×n），n为ANSYS热传导有限元模型的节点数目。对其他矩阵文件进行相同操作，得到相应的热传导矩阵、载荷列阵和热容矩阵。热传导矩阵需要进行LU分解。载荷列阵用于设置热源的损耗数值，通过LoadVector=LoadVector0+A*（LoadVectori-LoadVector0）+B*（LoadVectorj-Load-Vector0）+C*（LoadVectork-LoadVector0）+…，可以考虑第i个热源的损耗为A单位、第j个热源的损耗为B单位、第k个热源的损耗为C单位等多个热源同时作用的情况。

采用Krylov子空间投影法缩聚自由度后，可将n×n的矩阵降阶为n×r的矩阵v，其中降阶阶数r远小于原有阶数，因此，计算效率可比ANSYS有限元计算提高几百至几千倍，使得所需的计算时间和资源大大减少。降阶阶数对计算速度和计算精度有很大影响。降阶阶数过小时，计算速度很快，但计算精度变差；降阶阶数过大时，计算精度会更高，但会严重影响计算效率和存储资源。降阶阶数的确定主要依赖于时间范围、时间步长、损耗是否变化［2，5］。

根据大量的工程应用经验可知，如果后续步骤中需要对改变损耗的情况进行瞬态分析，且时间范围很小（如时间周期为0.001～1 s），相应的时间步长也很小，降阶阶数宜选取20～30。如果后续步骤中损耗不改变，且时间范围很大（如0.001～100 s以上），相应的时间步长可以较大，降阶阶数可取5～10。其余情况，建议取10～20。

时间步长可以采用定步长和对数步长的方法，对数步长方法可以在起始时间布置较多的时间点，有利于提高结果的准确性，因此，推荐采用对数步长方法。当使用某一固定的温度T0作为初始值时，初始温度场通过命令语句y0=v’*（T0*ones（n，1））来实现。降阶后的方程可以使用常微分方程求解器（ode15s）进行求解，时间范围（t1～t2）的计算取step次，可以得到（step+1）×r的矩阵Y，再通过命令语句y_reduced=（v*Y’）’将结果投影到原模型上，得到的y_reduced是（step+1）×n的矩阵。t2时刻的计算结果作为下一时间范围（t2～t3）的初始温度场时，可以通过命令语句y0=v’*y_reduced（step+1，：）’来设置。重复上述步骤，即可以实现热源不断改变条件下的循环计算。

经过结果投影到原模型，可以得到整个模型的节点温度。可以利用Matlab的patch命令显示温度场的分布云图，也可以利用max函数查找出最高温度及对应的节点编号，并以曲线的形式进行结果显示。

3 仿真条件

IGBT元件工作的过程中必须采取有效的散热措施，如强迫风冷、水冷、热管散热、微通道冷却等形式，不同散热方式的能力各不相同，散热器上的温度分布亦有很大区别。由于散热条件和均温性的组合甚多，为简化分析，可假设IGBT元件底面为某当量换热系数的散热条件［8-9］。假设某IGBT元件底面当量换热系数为500 W/m2·℃，IGBT芯片的平均损耗为650 W，二极管芯片的平均损耗为350 W。依据IGBT元件的几何结构建立如图2所示的ANSYS热传导有限元模型，网格单元数目80万，节点数目为91万。

图2 ANSYS热传导有限元模型Fig.2 Heat conduction finite element model by ANSYS software

IGBT元件中的IGBT芯片和二极管芯片依次交替产生热量，需要采用前面所述方法设置2个热源的损耗数值，然后提取热传导矩阵和热容矩阵，进行相应的矩阵操作、模型降阶、计算和结果显示。

4 基于平均损耗的计算结果

图3是对ANSYS热传导有限元模型进行稳态仿真得到的温度场分布结果，可以看出二极管芯片的温度最高，为87.243℃。图4是利用模型降阶程序进行时间范围0.01～10 000 s的计算后，得到的最高温度曲线。由温度变化曲线可知，温度先是迅速上升，然后变化趋势逐渐变缓，于100 s之后稳定在87.243℃。稳定后的温度值与ANSYS稳态计算的温度值非常吻合，说明了模型降阶方法可以得到非常准确的计算结果。从计算时间来看，模型降阶程序瞬态计算的时间约为ANSYS稳态计算的3倍，模型降阶方法在计算效率方面具有非常大的优势。

图3 IGBT元件温度场分布Fig.3 Temperature distribution of IGBT module

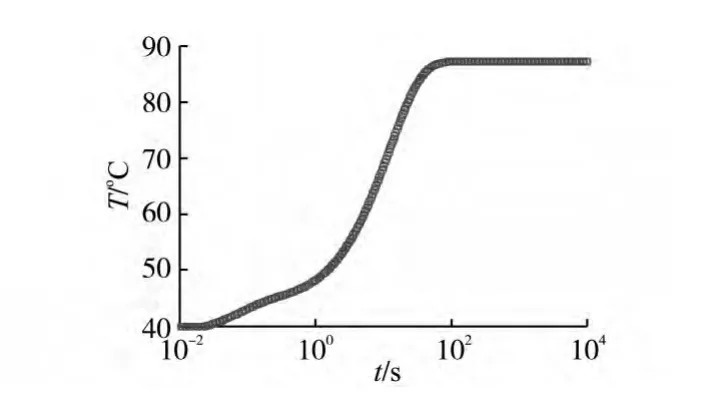
图4 最高温度变化曲线Fig.4 The highest temperature rise curve

5 输出频率对结温的影响

针对三相桥臂的一个IGBT元件，输出电流的正半周通过IGBT芯片时，IGBT芯片产生的损耗近似为半正弦波，输出电流的负半周通过二极管芯片时，二极管芯片产生的损耗亦近似为半正弦波，IGBT芯片和二极管芯片分别在另外半个周期内的损耗则为0。为了简化计算，通常假设损耗的脉冲波形为矩形或正弦半波［10-12］。

图5是假设IGBT芯片和二极管芯片损耗为方波，输出频率1 Hz（周期1 s）条件下的最高温度曲线。图5a示出的芯片最高温度变化曲线的规律与图4基本一致，由于损耗在矩形波和0之间波动，温度亦产生相应的波动。图5b是198～200 s之间IGBT芯片的最高温度变化曲线。在正半周期的损耗为定值，温度先是迅速升高，然后变化趋势减缓；损耗由定值突变为0的时刻，温度迅速下降；在负半周期的损耗为0，温度逐渐下降。图5c是198～200 s之间二极管芯片的最高温度变化曲线，由于二极管芯片和IGBT芯片交替产生损耗，在正半周期的损耗为0，温度逐渐下降，损耗由0突变为定值的时刻，温度开始上升；在负半周期的损耗为定值，温度先是迅速升高，然后变化趋势减缓。图5d表示了198～200 s之间2个周期的波形，相当于图5b和图5c叠加后的结果，最高温度在83.8～92.9℃范围内变化，与基于平均损耗计算的稳定温度相比，温度波动范围为-3.9%～6.5%。

图5 输出频率1 Hz的方波损耗对应的最高温度变化曲线Fig.5 The highest temperature change curve for the losses of square-wave in 1 Hz output frequency

图6和图7分别是输出频率5 Hz（周期0.2 s）和50 Hz（周期0.02 s）方波损耗条件下的最高温度曲线，其曲线变化趋势与输出频率1 Hz的基本一致，温度范围则有较大变化。输出频率5 Hz时，最高温度在84.5～90.2℃范围内变化，与基于平均损耗计算的稳定温度相比，温度波动范围为-3.1%～3.4%；输出频率50 Hz时，最高温度变化范围是86.9～88.3℃，与基于平均损耗计算的稳定温度相比，温度波动范围为-0.4%～1.2%。可以说明温度波动的范围随着输出频率的增加而逐渐减小。

图6 输出频率5 Hz的方波损耗对应的最高温度变化曲线Fig.6 The highest temperature change curve for the losses of square-wave in 5 Hz output frequency

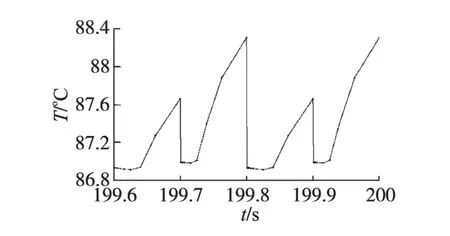
图7 输出频率50 Hz的方波损耗对应的最高温度变化曲线Fig.7 The highest temperature change curve for the losses of square-wave in 50 Hz output frequency

图8是假设IGBT芯片和二极管芯片损耗为半正弦波，输出频率1 Hz（周期1 s）条件下的最高温度曲线。图8a示出的芯片最高温度变化曲线的规律与图5a基本一致，但由于损耗波动幅度大，温度产生相应的波动亦大于方波的情况。图8b是198～200 s之间IGBT芯片的最高温度变化曲线。在正半周期的损耗为半正弦波，温度先是迅速升高，然后变化趋势减缓，温度在损耗为半正弦波峰值的时刻仍然继续上升，经历一小段时间后开始下降；在负半周期的损耗为0，温度逐渐下降。图8c为198～200 s之间二极管芯片的最高温度变化曲线。在正半周期的损耗为0，温度逐渐下降；在负半周期的损耗为半正弦波，温度先上升后下降，温度的峰值滞后于损耗半正弦波峰值的时刻。产生芯片结温的峰值相对于半正弦波损耗峰值有一定滞后的原因在于IGBT元件各层材料热容的影响。图8d相当于图8b和图8c叠加后的结果，在198～200 s之间有2个周期的波形，最高温度在81～93.9℃范围内变化，与基于平均损耗计算的稳定温度相比，温度波动范围为-7.2%～7.6%。

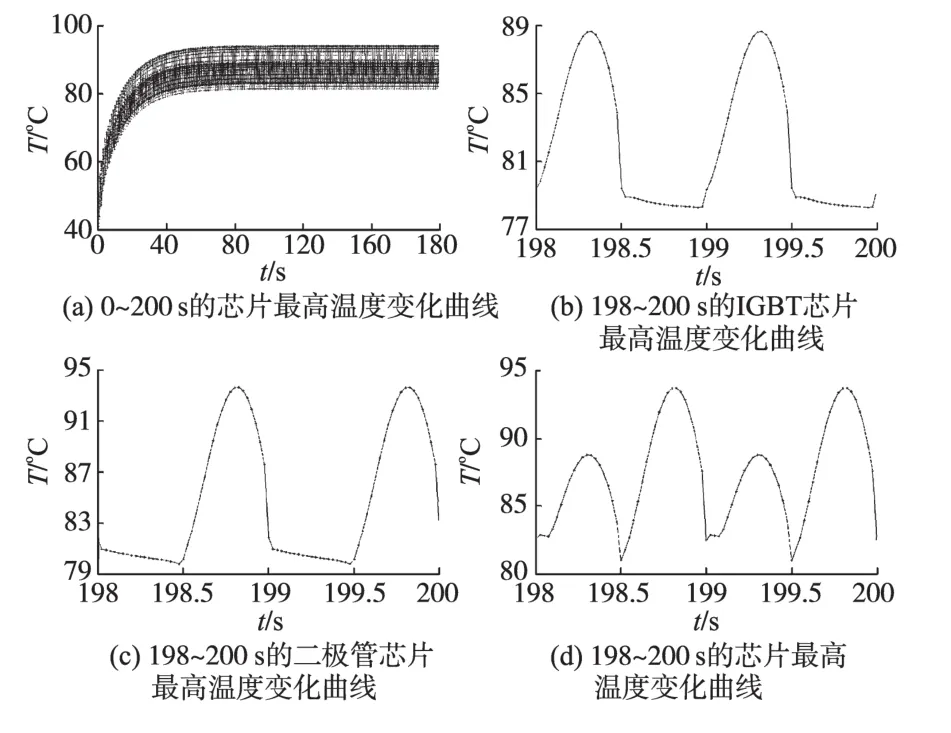
图8 输出频率1 Hz的半正弦波损耗对应的最高温度变化曲线Fig.8 The highest temperature change curve for the losses of half-sine wave in 1 Hz output frequency

图9和图10分别是输出频率5 Hz（周期0.2 s）和50 Hz（周期0.02 s）半正弦波损耗条件下的最高温度曲线。输出频率5 Hz时，最高温度在84～90.6℃范围内变化，与基于平均损耗计算的稳定温度相比，温度波动范围为-3.7%～3.9%；输出频率50 Hz时，最高温度则在86.4～88.4℃范围内变化，与基于平均损耗计算的稳定温度相比，温度波动范围为-1.0%～1.3%。同样可以说明随着输出频率的提高，芯片最高温度的波动逐渐减小。

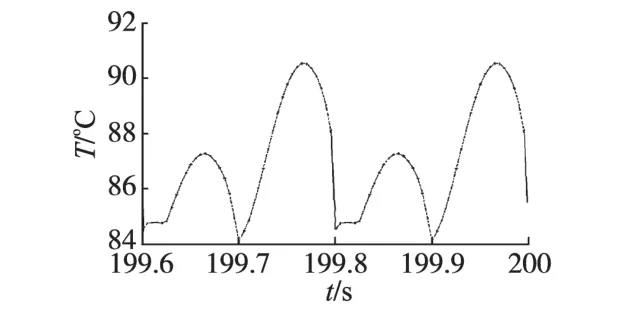
图9 输出频率5 Hz的半正弦波损耗对应的最高温度变化曲线Fig.9 The highest temperature change curve for the losses of half-sine wave in 5 Hz output frequency

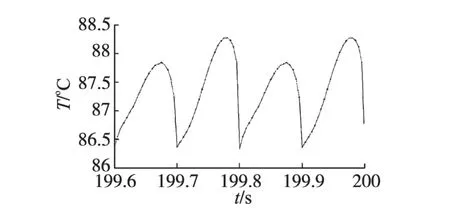
图10 输出频率50 Hz的半正弦波损耗对应的最高温度变化曲线Fig.10 The highest temperature change curve for the losses of half-sine wave in 50 Hz output frequency

由于半正弦波损耗的峰值是方波损耗值的π/2倍，通过对比输出频率分别为1 Hz，5 Hz和50 Hz时，方波损耗与半正波损耗导致的芯片最高温度波动范围可知：半正波损耗产生的温度波动范围大于方波损耗产生的温度波动；半正弦波损耗产生的最高温度要低于方波损耗，当输出频率增加至50 Hz时，两者最高温度波动的上限值相等，但半正弦波损耗产生的最高温度波动的下限值仍小于方波损耗。

5 结论

从方波和半正弦波损耗条件下的芯片最高温度变化趋势和波动范围对比可知，尽管平均损耗相同，损耗波形不同时，IGBT元件的瞬态热响应有差异，这种差异随着输出频率的提高而减小，随着输出频率的降低而增大，对IGBT元件结温波动的影响不可忽略。半正弦波损耗条件产生的温度波动要大于方波损耗条件，在简化计算时，需要予以注意。此外，通过长计算时间、多计算周期、损耗不断变化的复杂瞬态问题的快速有效计算，说明基于模型降阶的程序可以高效准确地解决瞬态问题，值得进一步推广应用。

［1］ 关乐，褚金奎，齐东周，等.基于二阶Krylov子空间投影法建立MEMS宏模型［J］.功能材料与器件学报，2008，14（1）：210-214.

［2］ Wilhelmus H A Schilders，Henk A van der Vorst，Joost Rom-mes.Model Order Reduction：Theory，Research Aspects and Applications［M］.Berlin：Springer，2008.

［3］ 关乐，褚金奎，齐东周，等.面向MEMS系统级仿真的宏模型研究［J］.系统仿真学报，2009，21（15）：4561-4567.

［4］ Rudnyi E B，Korvink J G.Model Order Reduction for Large Scale Engineering Models Developed in ANSYS［J］.Lecture Notes in Computer Science，2006，3732（1）：349-356.

［5］ Yang Y J，Yu C C，Shen K Y.MEMS Heat Transfer Arnoldi-based Macromodels and the Study of Minimum Required Or-ders［J］.Tamkang Journal of Science and Engineering，2005，8（3）：185-190.

［6］ 齐东周，褚金奎，关乐.MEMS降阶宏模型仿真平台研究［J］.微计算机信息，2009，25（3）：185-187.

［7］ 蒋耀林.模型降阶方法［M］.北京：科学出版社，2010.

［8］ 丁杰，唐玉兔，忻力，等.网格尺寸对IGBT水冷散热器仿真结果的影响［J］.大功率变流技术，2012，34（6）：26-30.

［9］ 丁杰，唐玉兔，忻力，等.IGBT模块封装的热性能分析［J］.机车电传动，2013，52（2）：9-12.

［10］侯少敏.高速动车组变流系统损耗分析与散热研究［D］.北京：北京交通大学，2011.

［11］唐勇，陈明，汪波.电力电子器件短时脉冲工作的结温特性研究［J］.电力电子技术，2010，44（3）：88-90.

［12］冯永杰，李斌，黄云.半导体器件功率老化的结温控制方法研究［J］.实验技术与管理，2010，27（5）：46-49.

修改稿日期：2013-11-01

Effects of Output Frequency on Junction Temperature Ripple for IGBT Module

DING Jie，TANG Yu-tu，XIN Li，HU Chang-fa
（CSR Research of Electrical Technology&Material Engineering，CSR Zhuzhou Institute Co.，Ltd.，Zhuzhou412001，Hunan，China）

In order to analyze the effects of output frequency on the fluctuation of junction temperature，the program based on the model order reduction method was developed，the temperature results was obtained and compared with steady state calculation results by ANSYS software，the consistency of results shows that the method is effective.The temperature change curves of IGBT module in different output frequencies were obtained by the program.According to the comparison between the stable temperature based on the average losses and the transient temperature，the results show that the range of temperature fluctuations produced by half sine wave losses in 1 Hz output frequency is-7.2%～7.6%，and the range of temperature fluctuations produced by square wave losses is-3.9%～6.5%，the effects on the temperature of IGBT module in 1 Hz output frequency is significant and less impact for the temperature of IGBT module while the output frequency is 50 Hz.The temperature fluctuation caused by half sine wave losses is greater than square wave losses.The analysis results can provide reference for IGBT transient temperature calculation，the program based on model order reduction can be further used in other power electronics devices transient temperature calculation.

insulated gate bipolar transistor（IGBT）；output frequency；junction temperature ripple；model order reduction

TM46

A

湖南省自然科学省市联合基金重点项目资助（12JJ8020）

丁杰（1979-），男，硕士，工程师，Email：dj8083@126.com

2013-08-06