单极性SPWM全桥电压纹波补偿

于宁，苑海涛，卢晓东，冯仁剑

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

单极性SPWM全桥电压纹波补偿

于宁，苑海涛，卢晓东，冯仁剑

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

单相逆变器在实际应用时，直流侧输入电压包含2倍于输出频率的纹波。纹波越大输出谐波含量越高。为抑制输入电压纹波的影响，在分析输入电压纹波来源及表现形式的基础上，提出一种根据其幅值与相位补偿开关管导通时间的改进型正弦脉宽调制技术（SPWM）。利用调制信号的周期特性，采用循环查表方式简化补偿策略，提高补偿速度。仿真及样机实验表明该调制方法可有效减小输入电压纹波对系统输出谐波的影响，提高输出质量。

单相逆变器；输入电压纹波；输出电压谐波；调制信号补偿；循环表查询法

1 引言

作为一种常用的能量转换工具，逆变器是光伏发电系统中的重要一环。实际工作时，由于波动输入电流在电源内阻上的作用，逆变器输入电压会产生2倍于系统输出频率的纹波［1-2］。纹波过大时将严重影响逆变器输出质量。

为抑制输入电压纹波的影响，逆变器可用输入电压矢量比较法、重复控制、电压电流双闭环［3］等控制方式削减输入电压纹波的干扰。多级式逆变器还可利用其结构特性，采用电流控制方法［4］减小直流母线电压波动，达到减小输出谐波含量的目的。但在调制方法上，常用的正弦脉宽调制、特定谐波消除、谐波注入等调制方法均基于恒定直流侧输入电压进行逆变调制，不能消除输入电压纹波的影响。为提高波动输入电压条件下系统输出质量，许多文献对调制方法进行改进。文献［5］在特定谐波消除方法上补偿输入电压纹波得到新的调制策略。特定谐波消除方法决定了该策略计算量大，实现起来较为困难。文献［1］提出一种根据输入电压纹波大小调节相应区段载波信号幅值的新型SPWM调制策略，该类方法仅局限于采用模拟控制方式，推广到数字控制实现则较为复杂。

本文在分析直流侧输入电压纹波的基础上，根据纹波形式补偿锯齿载波SPWM（以下简称SPWM）的调制信号，并用循环查表方式将改进后的SPWM实现。通过仿真及实验验证了该算法的有效性。

2 输入电压纹波分析

常见单相逆变器系统结构如图1所示。逆变器将蓄电池组供给的直流电经开关管调制后，由滤波电容滤除高次谐波含量，作为工频变压器输入侧电压，再经变压器升压输出为供负载使用的工频交流电。

图1 单级单相逆变器系统结构图Fig.1 System diagram of single-phase inverter

由文献［6］可知逆变桥输入电流与输出电流的关系式为

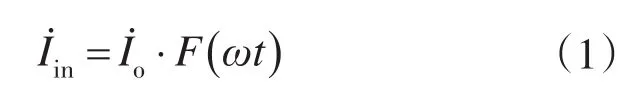
令变压器副边阻抗等效至原边的阻抗为Z=R+jωL，则逆变桥输出电压、输出电流关系为

当把逆变器输入端电源当作理想电源时

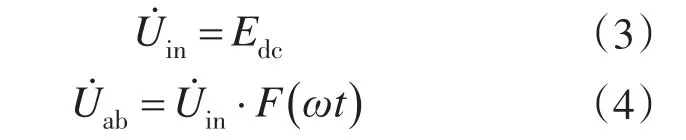
单极性SPWM逆变桥输出电压Uab的形式为

式中：M为调制系数；F为载波比。

忽略F(ωt)中幅值较小的高次谐波成分，其近似为Msin(ωt)。联立式（1）～式（4），并将F(ωt)=Msin(ωt)代入得

式中：φ为输入电压纹波最大值处与相应周期逆变调制信号起点的相位差，大小由负载与系统决定，集中在-π/2与0之间；K为电压纹波峰峰值与最大值E的比值。

3 纹波对输出电压的影响

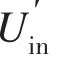
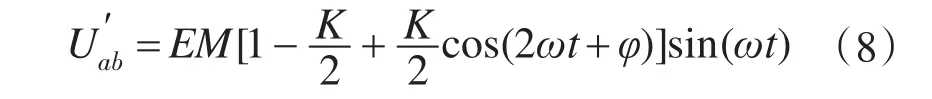
对式（8）进行傅里叶变换

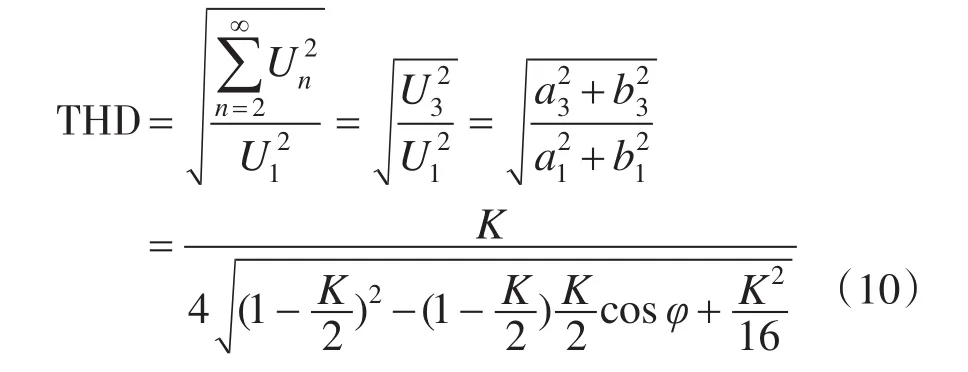
能够得出输出电压总谐波量与输入电压纹波K和φ的关系：φ一定时，K值越大THD越大；K一定时；φ从-π/2向0变化时THD单调递增，但变化不大。

4 抑制输入电压纹波影响方法

4.1 改进型SPWM

为抑制直流侧输入电压纹波的影响，即要求Uin经调制后的H桥输出电压除基波外不含谐波成分，本文提出的策略是对SPWM调制信号F(ωt)补偿输入电压纹波部分，得到改进后的调制信号F′(ωt)如下式：

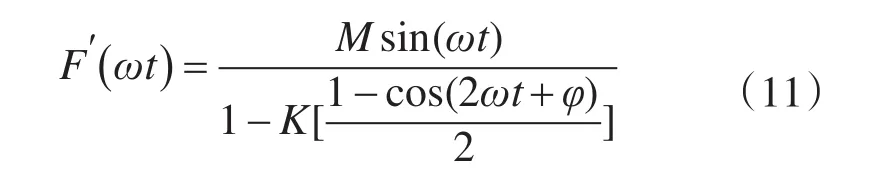
实现新逆变调制的必需步骤是获得补偿后的开关控制点，因此需要计算出F′(ωt)与锯齿载波的交点。

4.2 改进型SPWM的实现

改进型SPWM实质是根据纹波对各锯齿载波内的开关管导通脉宽长度进行补偿。如图2a中实线为输入电压，虚线为补偿信号；图2b中实线为补偿后调制信号，虚线为原调制信号。

图2 调制信号补偿示意图Fig.2 Modulation signal compensation

为降低控制策略的复杂度，进一步分析原调制信号F(ωt)与补偿信号，利用F′(ωt)的两点特性，实现数字控制方式。

1）特性1。SPWM调制信号，具有前半周期和后半周期对称特性。式（11）分母的补偿信号具有同样特性，仅存在待确定大小的K和φ。

2）特性2。当调制频率远高于正弦频率时，一个锯齿波周期内的正弦曲线可认为是平行于横轴的直线。根据三角形相似原理，Msin(ωt)在锯齿波一个周期内所截长度和sin(ωt)在同样锯齿波一个周期内所截长度的M倍相等。同理，Kcos(2ωt+φ)也有此特性。

根据特性1、特性2，先求得前半周期sin(ωt)与幅值为1锯齿波的一组交点，即各锯齿波周期开关管导通时间百分比，将此保存为开关数据表图3a。再求φ为0时[1-cos(2ωt)]/2与幅值为1锯齿波的交点，这组数据是起补偿导通时间作用的补偿数据表，形式见图3b。

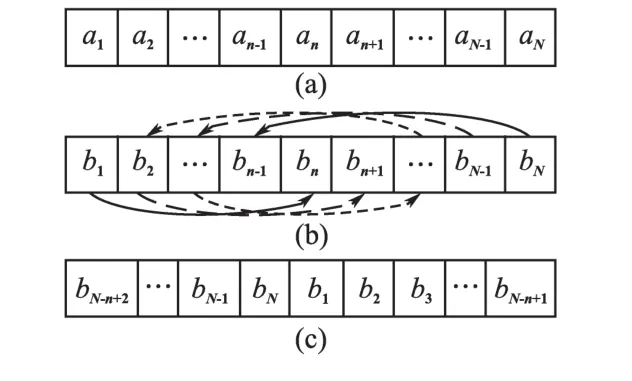
图3 循环查表法示意图Fig.3 Cycle table lookup algorithms

系统接入负载稳定运行时，参数K，φ和M为稳定值。M由控制输出电压大小的PI反馈环节获得。M与开关数据表图3a相乘得到式（11）分子。K与φ可由对输入电压的A/D采集数据处理获取。根据φ值大小将数据表图3b循环移动相应数目即得图3c。1减去K与图3c数据表的乘积得到分母。依次计算分子与分母序号对应项，得到改进型SPWM调制信号的开关导通数据表。按获取的开关控制点对逆变H桥进行控制，即可消除直流侧电压纹波的影响。

5 仿真与实验结果分析

5.1 仿真结果

为了检验本文提出的改进型SPWM的有效性，采用Matlab/Simulink仿真分析。按图1系统结构模拟逆变器，器件参数为：输入电源等效电阻电压0.01 Ω，24 V，输入侧滤波电容13.2 mF，滤波电感0.001 Ω，30 μH，输出侧滤波电容0.94 μF。通过设定负载电阻与电抗的大小改变K和φ。

图4为φ等于-π/6、不同K值下SPWM、改进型SPWM和式（10）的系统输出电压总谐波失真量。图4中，SPWM的THD随着K值增大而增大。式（10）所得结果与SPWM仿真结果大小接近。并且由图4中改进型SPWM仿真曲线可以看出，THD含量显著减小，K为10%时，THD含量为SPWM的14.2%。

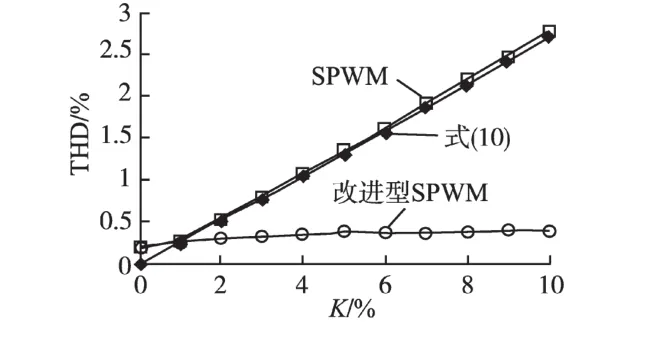
图4 φ定值、不同K值时THDFig.4 THD in sameφand different K

图5 K定值、不同φ值时THDFig.5 THD in same K and differentφ

图5为K等于5%、不同φ值下SPWM、改进型SPWM和式（10）的系统输出电压总谐波失真量。SPWM方式下THD随φ值变化略有改变，φ越靠近-π/2，THD越小。式（10）结果与SP-WM仿真结果相近。改进型SPWM下THD与SPWM的结果呈相似的变化，而大小约为后者的28%。

5.2 实验结果分析

实验分析时，设计了一台参数与仿真参数一致的试验样机。数字控制芯片采用STM32F103。为使小功率情况下纹波更为明显，输入24 V电源采用内阻较大的2节12V，40 A·h铅酸蓄电池串联。

图6a、图6b分别为200 W和100 W负载时输出电压Uout、输入电压Uin波形示意图。从图6a、图6b对比可以看出，负载功率越大输入电压纹波的幅度越大。输入电压波形上的高频信号是调制信号对测量带来的干扰。

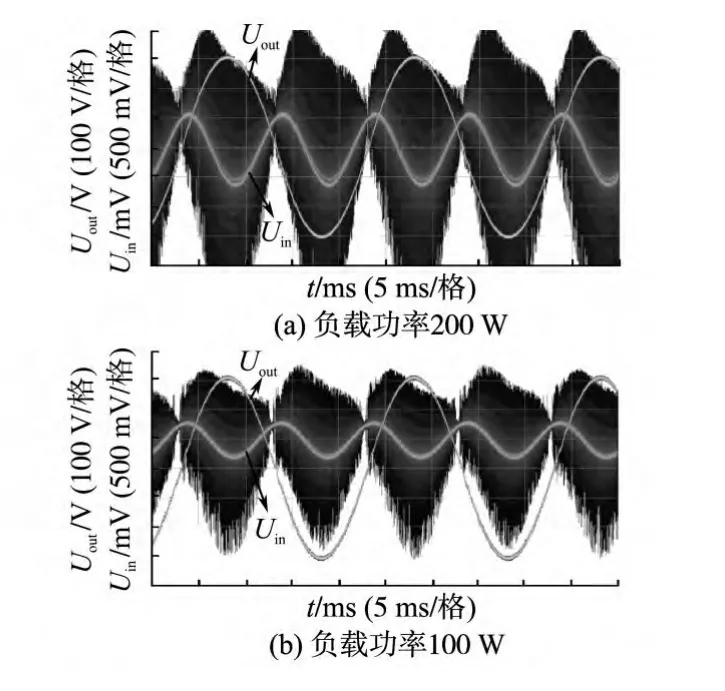
图6 带负载时系统输入输出电压Fig.6 System input and output voltage with load

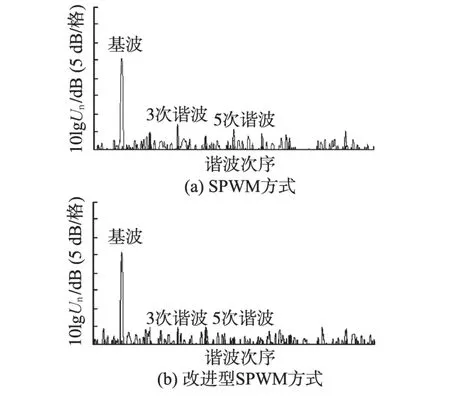
图7 SPWM及改进型SPWM输出谐波分析Fig.7 Harmonic analysis in SPWM and improved SPWM

图7a和图7b分别为200 W负载情况下SP-WM方式下输出谐波分析图和改进型SPWM方式下输出谐波分析图。图7a中，可以看到含量较大的3次谐波，THD大小为1.46%。而图7b与图7a相比，3次谐波的含量明显减小，且其他次谐波无明显增长，THD大小为0.67%。两图对比说明，改进型SPWM可减小输入电压纹波带来的输出谐波含量。

6 结论

本文在单相逆变器基础上，提出了一种抑制输入电压纹波影响的改进型SPWM。采用数字控制并用循环查表方式将其实现。仿真与实验表明：THD受负载电阻及电抗大小变化的影响，φ一定时，负载阻抗越小K值越大，THD越大，K一定时，THD随φ的改变无显著变化；改进型SPWM是针对逆变H桥输入直流电压纹波的补偿，所以该技术也可用于多级式逆变器逆变H桥，减小输出电压谐波量；本文提出的调制算法能够有效抑制因输入电压纹波产生的输出电压谐波，达到了较好的输出效果。

［1］ Jia-you L，York-yih S.Novel Sinusoidal Pulsewidth Modula-tion Schemes for Voltage-source Inverters with Fluctuating In-put Voltage［J］.IEEE Transactions on Industrial Electronics，1988，35（2）：284-294.

［2］ Changrong L，Jih-sheng L.Low Frequency Current Ripple Re-duction Technique with Active Control in a Fuel Cell Power System with Inverter Load［J］.IEEE Transactions on Power Electronics，2007，22（4）：1429-1436.

［3］ Naumanen V，Luukko J，Silventoinen P，et al.Compensation of DC Link Voltage Variation of a Multilevel Series-connected H -bridge Inverter［J］.IET Power Electron，2010，3（5）：793-803.

［4］ Anno Y，Seung-ki S，Hyeseung K，et al.Flux-weakening Strat-egy of an Induction Machine Driven by an Electrolytic-capaci-tor-less Inverter［J］.IEEE Transactions on Industry Applica-tions，2011，47（3）：1328-1336.

［5］ Damoun A，Ke Z，Cong L，et al.A Universal Selective Har-monic Elimination Method for High -power Inverters［J］.IEEE Transactions on Power Electronics，2011，26（10）：2743-2752.

［6］ Zhong C，Miao C，Yingpeng L，et al.Low Frequency Ripple Current Compensation with DC Active Filter for the Single-phase Aeronautic Static Inverter［C］//Energy Conversion Con-gress and Exposition（ECCE），Phoenix AZ，America，2011：1468-1475.

修改稿日期：2013-11-07

Single-phase Inverter Full Bridge Input Voltage Ripple Compensation on Unipolarity SPWM

YU Ning，YUAN Hai-tao，LU Xiao-dong，FENG Ren-jian
（School of Instrumentation Science and Opto-electronics Engineering，Beijing University of Aeronautics and Astronautics，Beijing100191，China）

In practical application，the DC input voltage of single-phase inverter contains an AC ripple at twice the output frequency.The ripple is larger，the output voltage total harmonic distortion is higher.In order to reject the input voltage ripple，an improved sinusoidal pulse width modulation technique was proposed.This method compensates switch signal with the ripple amplitude and phase，based on the analysis of the source and manifestation of the input voltage ripple.We take advantage of cyclical modulation signal，and adopt cycle lookup algorithms to simplify compensation strategies as well as improve the compensation speed.Simulation and experimentation results in single-stage single-phase inverter demonstrate that the proposed modulation technique is effective.

single-phase inverter；input voltage ripple；total harmonic distortion；switch signal compensation；cycle table lookup algorithms

TM464

A

国家自然科学基金资助项目（61001138；61201317）

于宁（1980-），男，博士，讲师，Email：nyu@buaa.edu.cn

2013-06-22