基于柔性神经网络的SRM直接瞬时转矩控制

党选举，袁小唐，胡景佳

（桂林电子科技大学电子工程与自动化学院，广西桂林 541004）

基于柔性神经网络的SRM直接瞬时转矩控制

党选举，袁小唐，胡景佳

（桂林电子科技大学电子工程与自动化学院，广西桂林 541004）

开关磁阻电机（SRM）有着广阔的应用前景，而低速运行时的高转矩脉动这一缺陷限制了其在汽车等领域内的应用。针对SRM强非线性和高度耦合性的特点，借鉴传统直接瞬时转矩控制（DITC）策略，提出了基于所构造的柔性神经网络（FNN）的SRM直接瞬时转矩控制策略。其中改进的控制策略外环采用不完全微分模糊PID对速度进行调节，内环采用以转矩误差的平方为性能指标函数的FNN自适应PID对转矩进行调节。在Matlab/Simulink环境下，仿真结果表明改进的DITC策略能够更有效地降低SRM的低速转矩脉动。

开关磁阻电机；直接瞬时转矩控制；模糊PID；柔性神经网络

1 引言

由于SRM的双凸极结构、开关式的供电方式和磁场的强非线性使噪声和转矩脉动问题较其它传统电机更加严重［1］。特别是电机在低速运行时，换相区的转矩脉动尤为明显，这严重制约了SRM在小轿车等各领域内的应用和推广。为了减少电机转矩脉动，国内外学者主要在电机设计和电机控制策略这两方面做了大量的研究，也取得了较多的研究成果［2］，在电机控制策略上取得的研究成果主要有转矩分配函数（torque-sharing function，TSF）控制策略［3］、直接转矩控制（direct torque control，DTC）策略［4］、迭代学习控制（iterativelearningcontrol，ILC）策略［5］、直接瞬时转矩控制（DITC）策略［6］等。

Robert B.Inderka等于2002年提出了DITC策略［6］，该控制策略主要是根据转矩偏差大小和不同转子位置区间选择不同的转矩滞环控制器，使电机的输出转矩基本保持在恒定值，并取得了较好的控制效果。SRM磁路和电路具有强非线性，尤其是电机的电磁特性极为复杂，无法有效地建立电机精确的数学模型，所以传统的控制算法，如PID难以达到令人满意的控制效果［7］。本文借鉴DITC策略，结合智能控制算法，外环采用不完全微分模糊PID控制器对速度进行调节，内环采用所构造的柔性神经网络对转矩偏差及电机的建模误差进行修正，在Mtalab/Simulink环境下，对所改进的DITC策略进行了仿真验证。

2 SRM的DITC系统分析

以6/4极三相开关磁阻电机为例，SRM的DITC系统如图1所示。

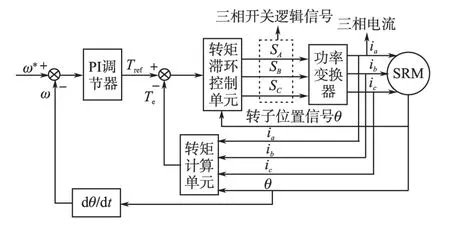
图1 SRM的DITC系统框图Fig.1 Block diagram of DITC based SRM control system

由图1可知，SRM的DITC系统主要包括PI控制器、转矩计算单元、转矩滞环控制单元和电机本体等。控制系统的外环是速度环，内环是转矩环。因为电机转速变化规律和转矩变化规律相一致［8］，而PI调节器是以比例环节调节为主，积分调节为辅的控制器，所以，速度偏差经过PI调节器可以看作参考转矩Tref，然后根据瞬时转矩Te得到转矩偏差。转矩滞环控制单元根据转矩偏差大小和转子位置区间选择不同的滞环控制器，得到三相开关逻辑信号SA，SB和SC。三相开关逻辑信号通过控制功率变换器的开关管的状态来控制相电压，进而驱动电机稳步运行。

功率变换器采用不对称半桥功率变换电路，根据功率变换电路的上下桥臂开关管的导通和关断情况，可以把每相分为1，0和-1 3个状态。当上下2个桥臂的开关管都导通时为状态1；1个开关管导通时为状态0，相电流通过1个二极管和导通的开关管组成回路续流；2个开关管都关断时为状态-1。SRM运行期间，根据在不同的转子位置导通相数的不同，把产生电磁转矩的区域分为换相区域和单相导通区域，在换相区域，电机的输出转矩由相邻两相共同承担；在单相导通区域，电机的输出转矩由导通相单独产生。在换相区域和单相导通区域，转矩滞环控制单元通过不同的转矩滞环控制器对转矩偏差进行调节，转矩滞环控制器产生的三相开关逻辑信号通过控制功率变换器开关管的通断来控制相电压，从而使电机在稳态时的输出转矩Te和参考转矩Tref基本相等，转矩脉动得到有效抑制。

以C相换相到A相为例，在换相区和单相导通区域，转矩滞环控制器的工作原理如图2所示，其他相邻相的换相原理相同。

图2 基于DITC策略的转矩滞环控制器工作原理图Fig.2 Schematic diagram of DITC strategy based torque hysteresis controller

3 SRM直接瞬时转矩控制

开关磁阻电机是一个变结构、变参数的强非线性控制系统，无法有效地建立精确的数学模型［9］，用传统的控制算法（如PID）不能达到理想的动态性能和稳态性能。本文在传统DITC策略的基础上，引入智能控制算法：速度环用不完全微分模糊PID调节器对速度进行调节；转矩环用FNN自适应PID对转矩进行调节。基于FNN网络的SRM直接瞬时转矩控制系统框图如图3所示。

图3 基于FNN的SRM直接瞬时转矩控制系统框图Fig.3 Block diagram of SRM direct instantaneous torque control based on FNN

3.1 不完全微分模糊PID速度调节器的设计

如图4所示，二维模糊控制器的输入为速度偏差e和速度偏差的变化ec。二维模糊控制器相当于一个参数可变的PD控制器，本身没有积分环节，因此会存在稳态误差［10］，有必要对二维模糊控制器进行优化，设计一个积分环节和二维模糊控制器并联，并联后的控制器结构可以看成是参数可变的PID控制器，积分环节用来消除系统静差。积分系数根据公式km=λ1+λ2/(||e+λ3)进行自适应调节，在该文的仿真系统中，|e|是速度偏差的绝对值，λ1，λ2和λ3为常量。

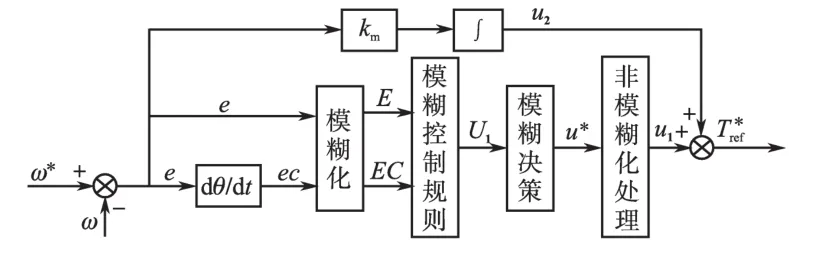
图4 积分并联的模糊PID控制器结构Fig.4 Structure of integral paralleling fuzzy PID controller

在模糊PID速度调节器后面引入一阶惯性环节（即低通滤波器）G(s)=1/(1+Ts)，构成不完全微分模糊PID速度调节器，如图3虚线框所示，这样既保留了微分环节的优良特性，又避免了速度扰动在纯微分作用下可能带来的高频干扰。

速度偏差e和速度偏差的变化ec通过量化因子变换到相应的模糊集论域，在模糊离散论域，误差E、误差的变化率EC以及模糊控制器的输出U的隶属度函数如图5所示，语言值NB，PB均采用Z型隶属度函数，其他的语言值均采用三角型隶属度函数。

图5 隶属度函数曲线Fig.5 Curves of membership functions

模糊控制规则表征了模糊控制输入量和模糊控制量之间的关系。本文所采用的模糊控制规则如表1所示。

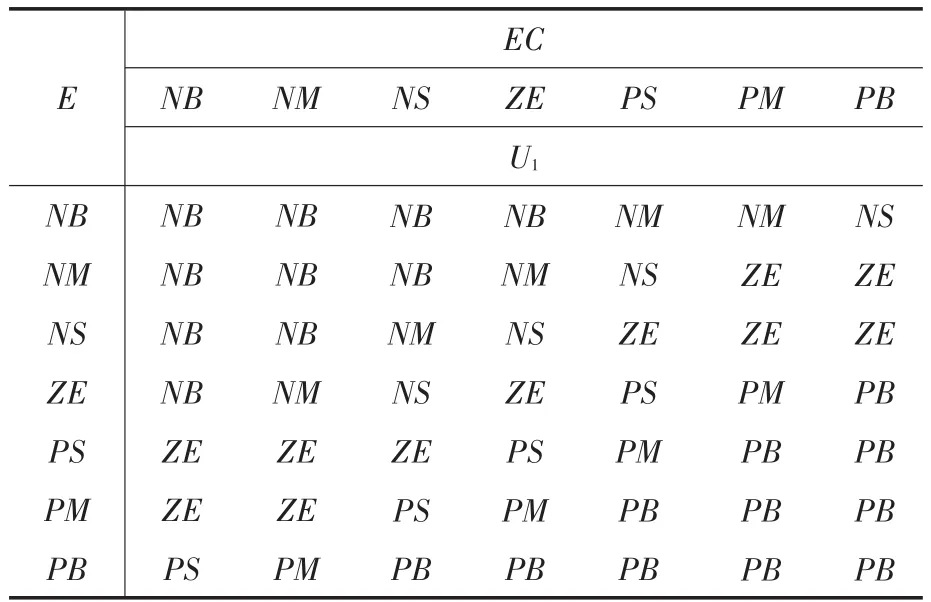
表1 模糊控制规则表Tab.1 Fuzzy control rules

本系统采用“重心法”来求取模糊决策的输出量，再通过量化因子转换到控制对象所能接受的基本论域中去。

3.2 基于柔性神经网络（FNN）的PID转矩控制器的设计

构造的柔性神经网络（FNN）PID控制结构如图6所示，主要由柔性神经网络学习结构和增量式PID两部分组成。柔性神经网络采用最速下降法对权值进行修正，结构上特点是：隐含层和输出层激励函数的参数均是可调整的，可加快神经网络的学习速度；能有效地防止神经元激励函数进入假饱和状态而使网络权值不能被修正。

图6 基于构造的柔性神经网络PID控制器结构Fig.6 Structure of the PID controller based on constructed flexible neural network

如图7所示，构造的柔性神经网络学习结构采用4-6-3网络结构，输入矢量x=[Tref，Te，e(k)，1]，这样隐含层节点阈值就可以并入到权值矢量中进行在线调整，网络的输出是PID控制器的3个参数kp，ki，kd。

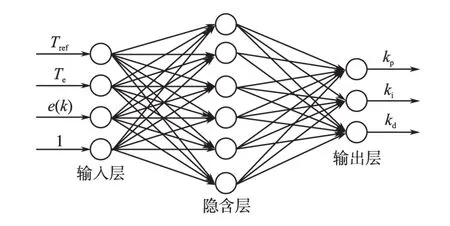
图7 柔性神经网络学习结构Fig.7 Learning structure of flexible neural network

构造的柔性神经网络结构隐含层节点的激励函数选取为柔性双极性S函数［11］：

式（1）函数对x和a的偏微分表达式分别为

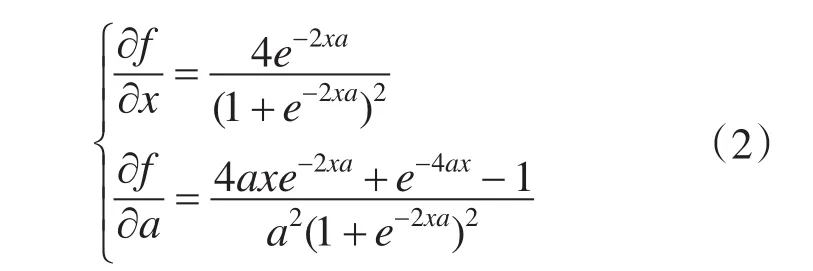
网络输出层节点的柔性激励函数取

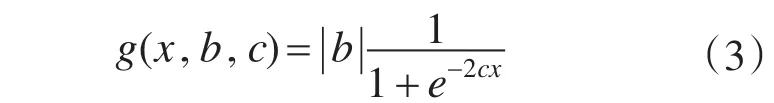
式（3）函数对x、b和c的偏微分分别为

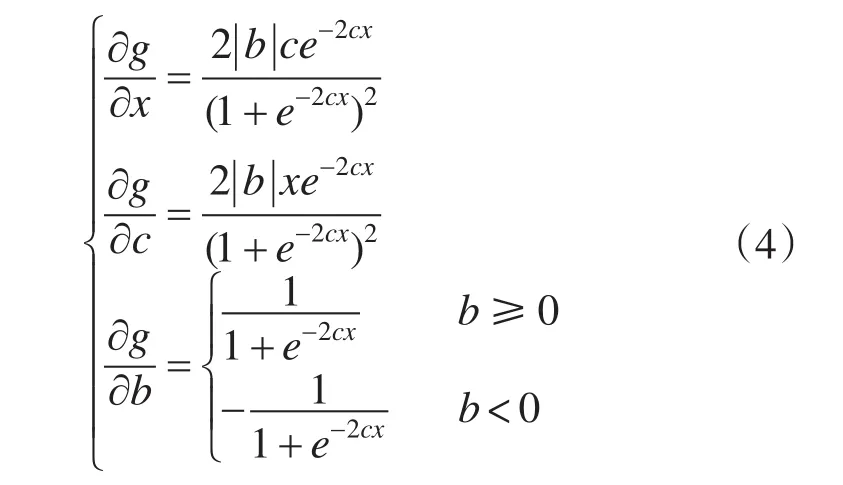
FNN学习采用误差反馈学习方法，设其性能指标函数为

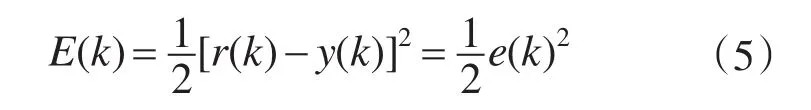
式中：r(k)为参考转矩信号；y(k)为电机输出的瞬时转矩信号。

FNN的权值和激励函数的参数根据梯度下降法进行在线调整，输出层调整算法为

式中：ωlj，bl，cl分别为网络隐含层第j个节点和输出层第l个节点之间的权值，输出层第l个节点激励函数的b参数及输出层第l个节点激励函数的c参数。

为了加快算法的收敛速度和在一定程度上克服局部极小值问题，一般都采用带动量项的梯度法［12］，α为动量因子。β和η分别表示权值和参数调整的学习率。

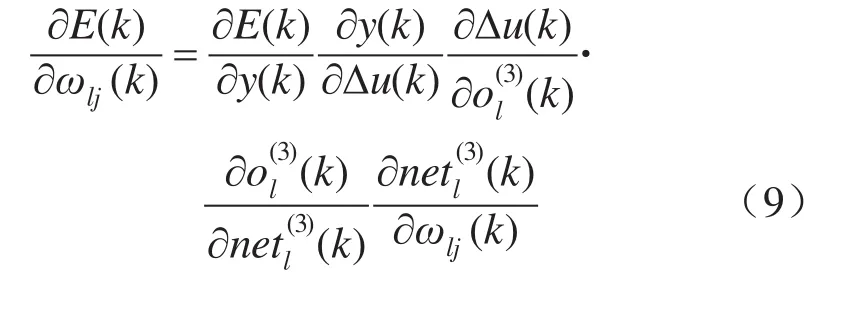
同理可得

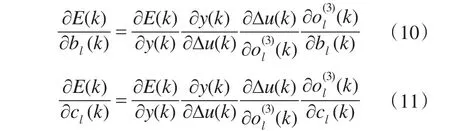
由 于 ∂y(k)/∂Δu(k)未 知 ，所 以 用 符 号 函 数sgn(∂y(k)/∂Δu(k))来近似取代，由此带来的计算误差可以通过学习率的调整来进行修正。

隐含层的调整算法为

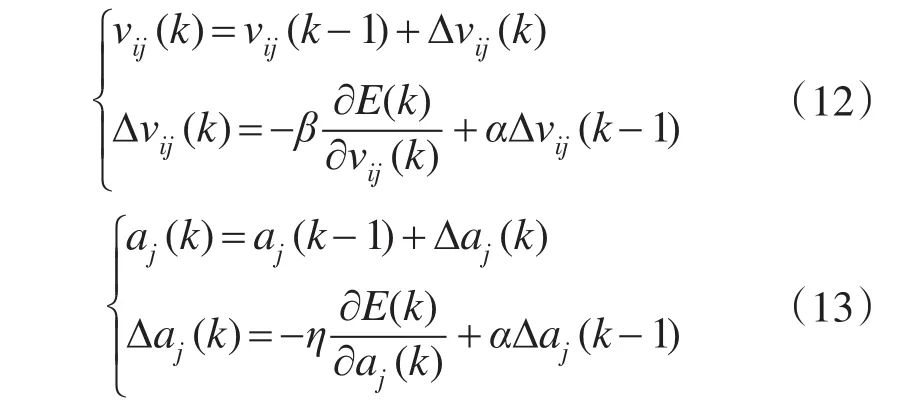
式中：νij，aj分别为网络输入层第i个节点和隐含层第j个节点之间的权值，隐含层第j个节点激励函数的参数a。

4 仿真验证与分析

为了验证上述控制策略的正确性，在Matlab/Simulink环境下建立6/4极SRM控制系统仿真模型。SRM模型选择Simulink自带的电机模型，电机主要参数设置为：Lmin=0.67 mH，Lmax=23.62 mH，定子绕组电阻Rs=0.05 Ω，磁链最大值Ψmax=0.48 Wb，直流电源电压VDC=240 V，电机负载TL=8 N·m，电机运行转速n=150 r/min。

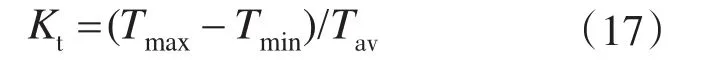
式中：Tmax，Tmin，Tav分别为电机达到稳态后的最大瞬时转矩，最小瞬时转矩及平均电磁转矩。

图8a为传统DITC策略下的转矩波形仿真结果。图8b为改进的DITC策略下的转矩波形。图9a和图9b分别表示电机在传统DITC策略下和在改进的DITC策略下瞬时转矩误差波形图。由图9a和图9b可知，改进的DITC策略下的瞬时转矩误差明显减小。图10为传统DITC策略和改进的DITC策略下电机达到稳态后的转矩误差波形对比图，其中虚线和实线分别表示传统DITC策略下的转矩误差波形和改进的DITC策略下的转矩误差波形，达到稳态后转矩参数如表2所示，传统的DITC策略下的转矩脉动系数约为0.040 72，改进的DITC策略下转矩脉动系数为0.019 22，降低约2倍。

图8 传统DITC和改进DITC策略下的转矩波形Fig.8 Torque curves of traditional DITC strategy and improved DITC strategy

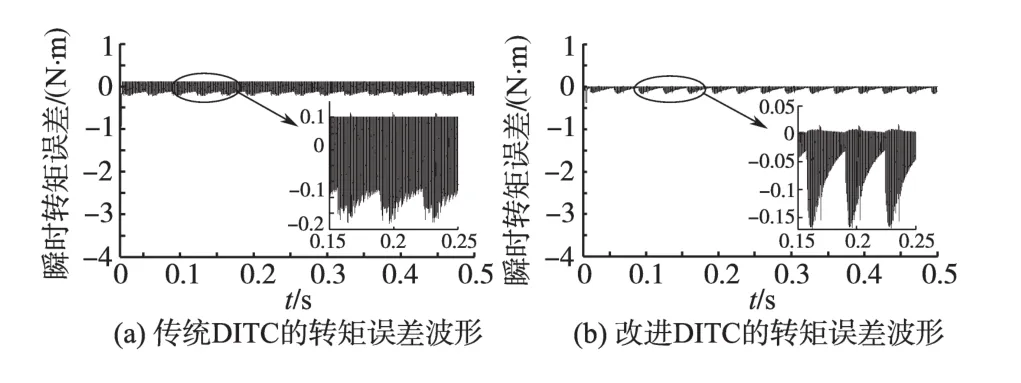
图9 传统DITC和改进DITC策略下的转矩误差波形Fig.9 Torque error curves of traditional DITC strategy and improved DITC strategy

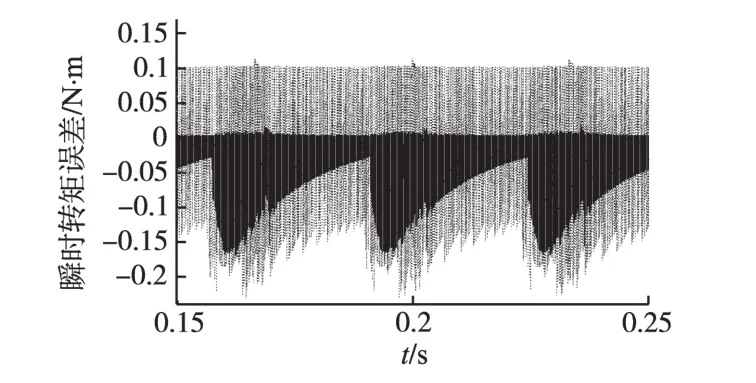
图10 转矩误差波形对比图Fig.10 Comparison pictrue of torque error waveforms

表2 转矩脉动系数Kt对比Tab.2 Comparison of toqrue ripple factorKt

5 结论

本文借鉴传统DITC策略，针对SRM的强非线性和高度耦合的特点，引入智能控制算法，提出了基于所构建的柔性神经网络SRM直接瞬时转矩控制策略。该策略的外环为速度环，通过不完全微分模糊PID控制器对速度进行调节；内环为转矩环，以瞬时转矩误差的平方为性能指标函数，FNN自适应PID实现了对瞬时转矩的调节。仿真结果表明，SRM在低速运行时，所提出的直接瞬时转矩控制策略较传统DITC策略具有更好的转矩脉动抑制效果。

［1］ 孙剑波，詹琼华，王双红，等.开关磁阻电机减振降噪和低转矩脉动控制策略［J］.中国电机工程学报，2008，28（12）：134-138.

［2］ 周素莹，林辉.减少开关磁阻电机转矩脉动的控制策略综述［J］.电气传动，2008，38（3）：11-17.

［3］ Xue X D，Cheng K W E.Optimization and Evaluation of Torque-sharing Functions for Torque Ripple Minimization in Switched Reluctance Motor Drives［J］.IEEE Transactions on Power Electronics，2009，24（9）：2076-2090.

［4］ 俞枭辰，王家军，宋小川.基于Simulink的8/6极开关磁阻电动机的直接转矩控制仿真［J］.机电工程，2013，30（03）：333-338.

［5］ 李红梅，张志全，李忠杰.减小小功率开关磁阻电机转矩脉动的迭代学习控制［J］.电工技术学报，2006，21（10）：67-70.

［6］ Robert B Inderka，Rik W De Doncker.DITC-direct Instanta-neous Torque Control of Switched Reluctance Drive［C］//IEEE 37th IAS Annual Meeting，2002.USA：IEEE，2002：1605-1609.

［7］ 王勉华，王瑞，刘春元.基于神经网络的SRM直接转矩控制系统仿真研究［J］.微电机，2013，46（1）：55-58.

［8］ 王勉华.SRM直接转矩控制调速系统结构研究［J］.电气传动，2012，42（8）：3-5.

［9］ 梁媛媛.开关磁阻电机直接转矩模糊PI控制系统研究［D］.西安：西安科技大学，2008：33-35.

［10］詹琼华，殷春辉.查表型模糊控制器在SR调速系统中的应用与优化［J］.微电机，2006，39（4）：4-7.

［11］王洪元，史国栋，夏德深.柔性神经网络及其应用［J］.模式识别与人工智能，2002，15（3）：372-376.

［12］党选举，谭永红.基于神经网络的热电偶传感器的智能信号处理［J］.计算机工程，2004，30（6）：25-26.

［13］潘再平，罗星宝.基于迭代学习控制的开关磁阻电机转矩脉动抑制［J］.电工技术学报，2010，25（7）：51-55.

修改稿日期：2013-11-22

Direct Instantaneous Torque Control of SRM Based on Flexible Neural Network

DANG Xuan-ju，YUAN Xiao-tang，HU Jing-jia
（School of Electronic and Automation，Guilin University of Electronic Technology，Guilin541004，Guangxi，China）

Switched reluctance motor have broad application prospect.However，high torque ripple is a serious drawback at low speed，and limits its widespread application on the automobile industry and other fields.SRM direct instantaneous torque control strategy based on constructed flexible neural network was proposed，which refers to the ideas of traditional direct instantaneous torque control to solve the strong nonlinear and high coupling of the SRM.In the improved control strategy，the outer-loop incomplete derivative fuzzy-PID is used to adjust the motor speed，and the inner-loop flexible neural network self-adaptive PID is employed to regulate the motor torque by using the square of the torque error as performance index function.In the Matlab/Simulink environment，simulation results prove that the improved DITC strategy proposed reduces the torque ripple of the SRM more effective at low speed，comparing with the traditional DITC strategy.

switched reluctance motor（SRM）；direct instantaneous torque control（DITC）；fuzzy-PID；flexible neural network（FNN）

TM352

A

国家自然基金项目（60964001，61263013）；广西教育厅重大项目（201101ZD007）；广西信息科学实验中心重大项目（20130110）

党选举（1965-），男，博士，教授，Email：xjd69@163.com

2013-05-07