混合式双级矩阵变换器的简化调制方法

熊剑，胡彦奎，王红红，李乾宇

（兰州交通大学自动化与电气工程学院，甘肃兰州 730070）

混合式双级矩阵变换器的简化调制方法

熊剑，胡彦奎，王红红，李乾宇

（兰州交通大学自动化与电气工程学院，甘肃兰州 730070）

为了解决混合式双级矩阵变换器（混合式TSMC）直流侧电压波动较大，以及控制策略复杂的问题，为此对整流级提出一种简化的脉宽调制方法（PWM），该方法占空比计算简单，而且能使整流级在一个开关周期内输出直流电压为常数，便于逆变级应用SVPWM方法调制，综合了常规算法的优点。最后在Matlab/Simull-ink中进行了建模和仿真，验证了新调制方法的正确性。

混合式双级矩阵变换器；整流级；脉宽调制；占空比；调制方法

1 引言

矩阵变换器作为一种交-交变换器，有优于传统电力变换器的优点。其输出电压、频率可调；输入功率因数接近1；具有无中间储能环节，体积小，结构紧凑；能量实现双向流动等优点，因此矩阵变换器在交流传动系统中具有一定的应用价值。双级矩阵变换器不仅与矩阵变换器有相同的性能，而且开关器件较少，换流简单，但其控制策略复杂，限制了矩阵变换器在实际工业中的应用［1-2］。

混合式TSMC以双级矩阵变换器为基础的新型拓扑结构的矩阵变换器。具有双级矩阵变换器优点的同时，还在直流环节串了一个由H桥控制电容充放电的电路来调节直流电压，有更高的电压传输比，能抑制输入电压不平衡和负载扰动。是目前非常具有潜力的一种新型矩阵变换器。

混合式TSMC的拓扑分为3个部分。前端是整流级、中间是H桥、最后输出为逆变级。其调制方法也是由以上3个部分的调制方法组合构成。当前，整流级的调制方法有两种：一是脉宽调制，二是空间矢量脉宽调制。H桥控制相对简单，只有两种开关状态，这里不作陈述。逆变级大多采用SVPWM。如整流级用SVPWM需合成矢量判断扇区。需要进行坐标变换，并且占空比的计算中含有三角函数，计算相当复杂。文献［3-4］应用的PWM方法中占空比计算精简，但中间平均直流电压是变化的。为了跟随这变化的平均直流电压，需要对逆变级的调制比进行实时更正。为了让混合式TSMC控制简单，便于工业应用。本文提出一种新的精简调制方法应用于前端整理部分。此方法占空比算法简单，计算量少，并能使整流级在一个开关周期内输出直流电压为常数，便于逆变级应用SVPWM方法调制，综合了常规算法的优点［5］。

2 整流级的新型精简调制方法

混合式TSMC的拓扑结构如图1所示。ia，ib，ic，ua，ub，uc为三相输入电流和电压；Sxp，Sxn分别是整流级上下桥臂的双向开关；Syp，Syn分别是逆变级上下桥臂的双向开关；iu，iv，iw为三相输出电流；L1，C1分别为输入滤波器的电容和电感；L2，C2为三相负载，udc为直流电压。

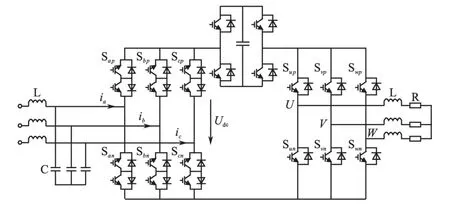
图1 混合式TSMC的拓扑Fig.1 The topology structure of hybrid TSMC

整流侧的调制目的有两点：一是在一个开关周期内，输出电压平均值为常值，并获得最大的电压利用率；二是使输入电流跟随输入电压按正弦规律变化，使输入侧功率因数为1。

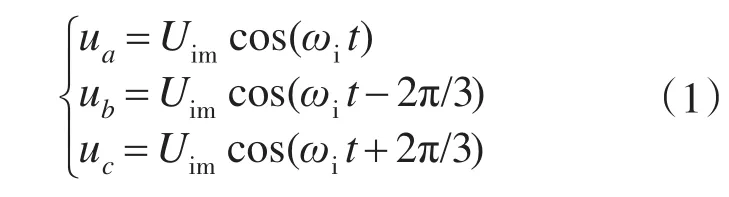
式中：Uim为电压的幅值；ωi为输入角频率。

将输入相电压一个周期分成6个区间，任意区间的两相相电压值极性相同，且第3相电压极性相反绝对值最大，如图2所示。

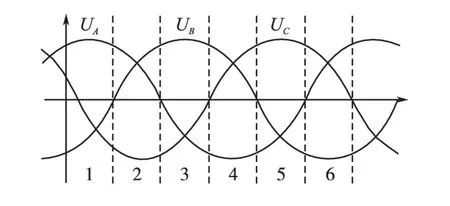
图2 三相输入电压波形及扇区划分Fig.2 Three-phase input voltage waveforms and vectors demarcation

目的1：使输出直流电压udc尽可能的大，以及更高的电压利用率，则需要在一个周期内，用幅值差较大的线电压来合成udc。目的2：要使udc在每一个开关周期的平均值为常数，这时需要用零电压（uaa，ubb，ucc）来调整平均直流电压。为达到上述目的，在此将每个开关周期分为3段。由图2可知，在区间1内，幅值差较大的2个线电压，即ua-ub，ua-uc，则在一个开关周期的第1阶段udc=uab；第2阶段udc=uac；第3阶段udc=uaa=0。同理可得其余5个区间的开关状态，如表1所示。

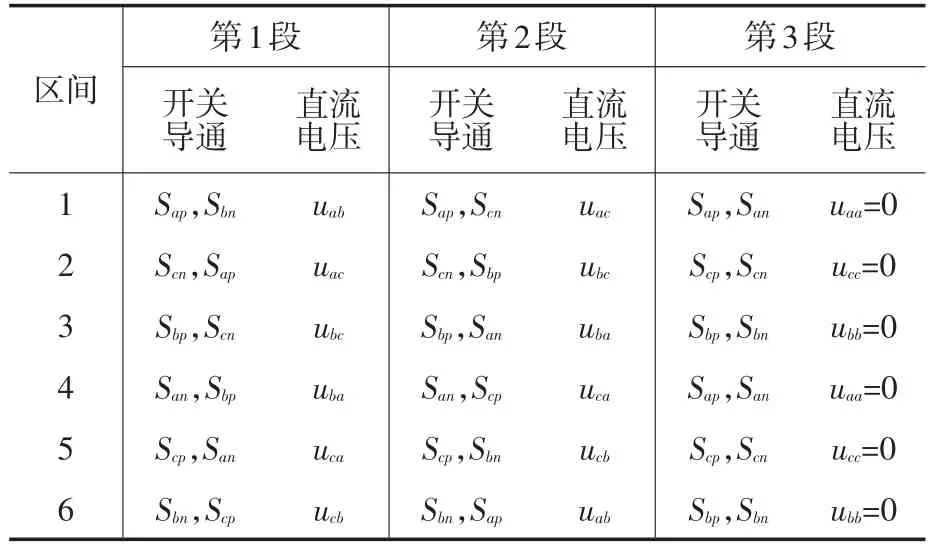
表1 整流级开关状态Tab.1 Switching states of rectifier

在采样频率远远高于工频时，线电压在这个高频周期内可看作一个定值，这个定值可以用采样点的值来代替。假定在第1区间时，Udc为整流侧输出最大平均直流电压。则有：

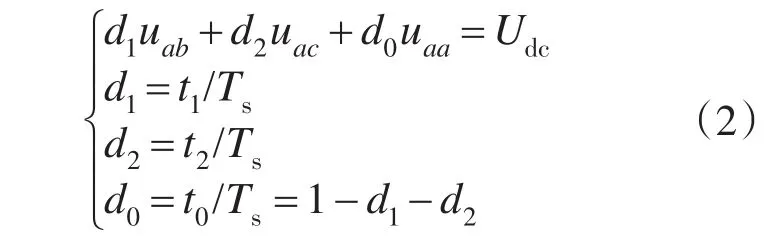
式中：d1，d2，d0，t1，t2，t0分别为3个阶段的占空比和持续时间；Ts为开关周期。

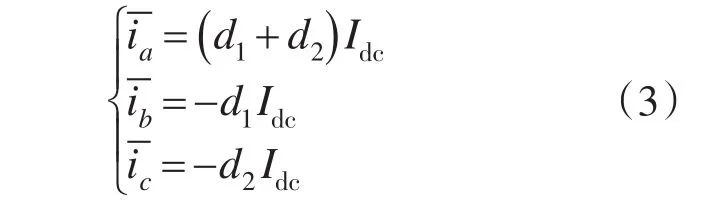
由于要使输入侧功率因数为1，则每相的输入电压和电流同相位。所以有：

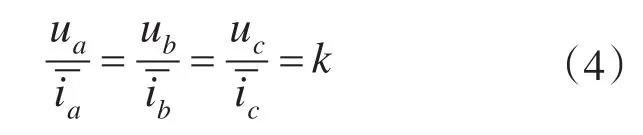
由式（2）～式（4）求解得：

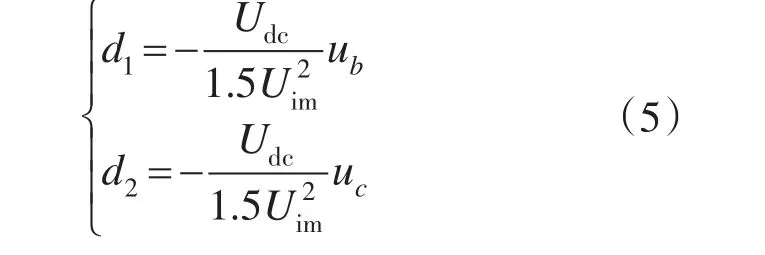
由于3个占空比的值均大于等于零，则由式（2）的第4式变形得：

由式（1）、式（5）、式（6）联立解得：

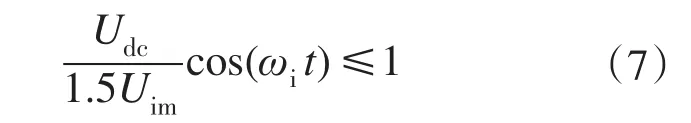
因为假定在第1区间，则有-π/6≤ωit≤π/6，代入式（7）得Udc≤1.5Uim，则Udc(max)＝1.5Uim，将Udc(max)代入式（5）可求得占空比的表达式为

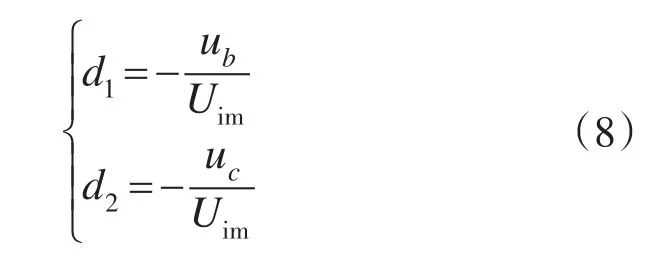
依此类推，可以求得其余5个区间时占空比的表达式。

此方法在判断电压分区，可以由三相电压瞬时值的正负来判断。在占空比的计算方面，占空比等于相应的相电压测量值与Uim相除。综上所述，新的精简调制方法计算简单，并且在一个开关周期内合成的平均直流电压值为常数，有利于SVPWM调制方法在逆变级中的应用［6］。

3 H桥变换器调制策略

图3为H桥拓扑。它的开关组合状态为［SL1SˉL1SL2SˉL2］，1 表示开通，0 表示关断。通过控制H桥变换器，把电容当作可控电压源。当整流级输出的局部平均电压值小于逆变级输入电压参考值时，开关组合为［0 1 1 0］，此时H桥变换器的输出电压和整流级输出电压极性相同，电容和电网一起给负载供电，电容电压下降，提高了逆变级的输入电压；相反，当开关组合为［1 0 0 1］，整流侧输出电压与H桥变换器输出电压极性相反，电容吸收能量，逆变侧的输入电压降低。

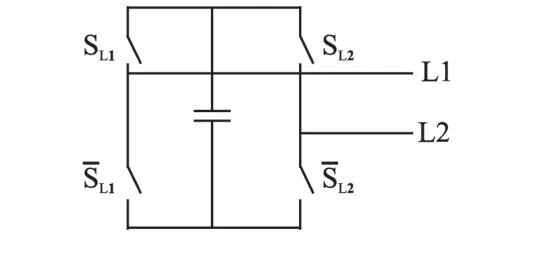
图3 H桥变换器拓扑Fig.3 The topology of H-bridge converter

4 逆变级调制策略

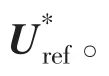
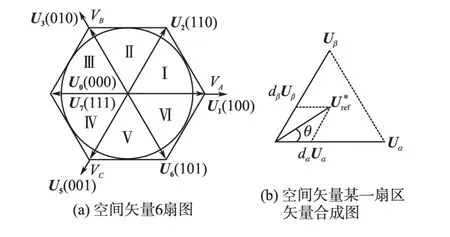
图4 空间矢量合成图Fig.4 Composition graph of space vector

由空间矢量调制原则以及正弦定理求得各矢量的作用时间：

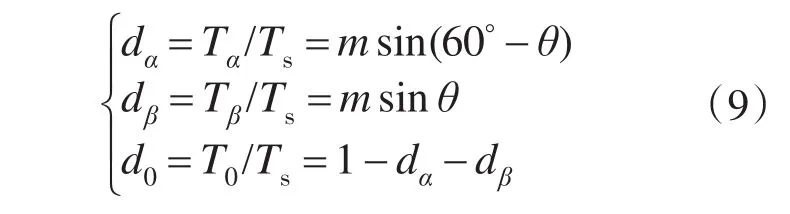
即得到：

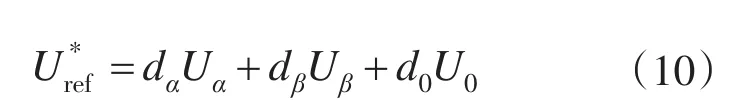
式中：m为调制系数；Ts为采样周期；Tα，Tβ，T0为Uα，Uβ，U0在一个采样周期中的作用时间；dα，dβ，d0为占空比。

SVPWM与传统的正弦脉宽调制（SPWM）相比不仅提高了直流电压利用率和动态响应速度，还降低了输出波形中所含的谐波量，并且便于数字化实现［10］。

5 仿真分析

论文所用仿真软件为Matlab7.1/Simulink，PWM周期为0.01 ms，其中混合式TSMC的双向开关用理想功率开关器件代替。输入LC滤波器L=5.5e-3 H，C=60e-6 F，负载（阻感性）R=5 Ω，L=5e-3 H。输出LC滤波器L=1 mH，C=5e-5 F。

图5为整流级输入侧a相电压、电流波形。都为正弦波，由于滤波器的关系，输入电流的相位略超前输入电压。

图6为整流侧输出直流电压波形，脉动的直流电压，幅值在220～380 V之间，与理论值吻合。

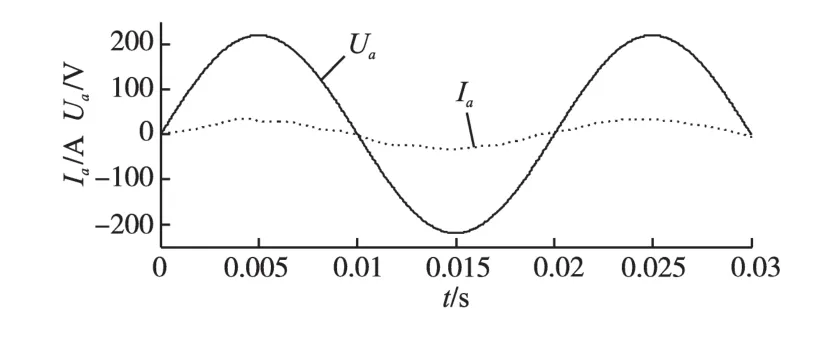
图5 整流级输入侧a相电压、电流Fig.5 a-phase voltage and current of rectifier input

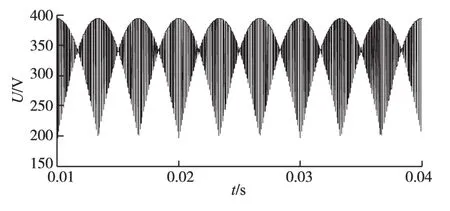
图6 整流级输出直流电压Fig.6 The DC voltage of rectifier output

图7为逆变级输出侧的电流以及电压波形。电流波形为正弦波，电压波形为PWM波形。它的频率以及相位与逆变侧给定的调制信号相对应。由于负载为阻感性负载，因此其电压相位略超前于电流相位，和预想情况一样。

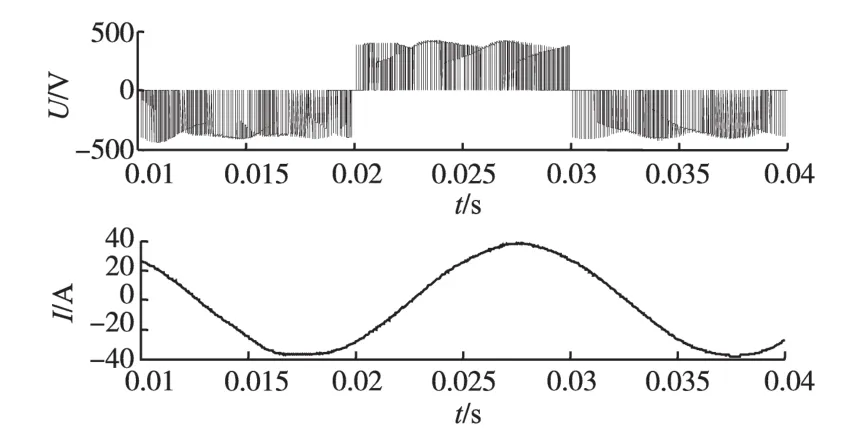
图7 逆变级输出电压、电流Fig.7 Voltage and current of inverter input

图8和图9分别为滤波前和滤波后的三相输出线电压。图8中三相输出线电压波形基本为PWM波，该PWM波的频率和相位与给定的调制信号是相同的，但存在一定的谐波；图9为滤波后的电压波形，成正弦规律变换，符合负载要求。

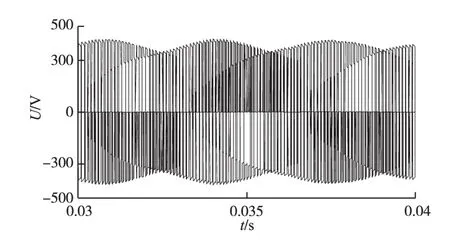
图8 未加滤波器的三相输出线电压Fig.8 Without a filter of three-phase output line voltage

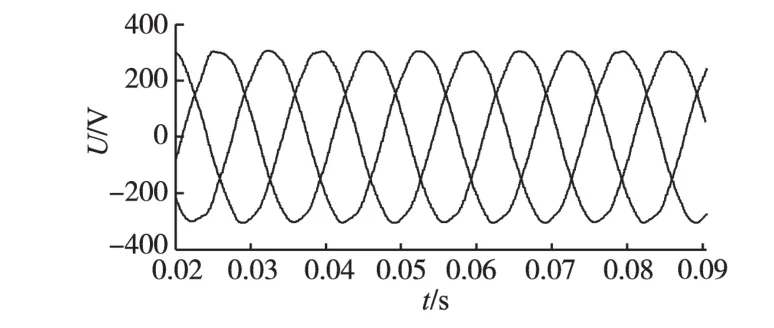
图9 加滤波器后的三相输出线电压Fig.9 With a filter of three-phase output line voltage

6 结论

本文针对混合式TSMC控制策略复杂及直流电压波动问题。对整流级提出了一种新的简化调制方法，其算法简单，计算量少，而且能使整流级在一个开关周期内输出直流电压为常数，便于逆变级应用SVPWM方法调制，综合了常规算法的优点。推导出了完整的占空比计算公式。并且应用Matlab7.1/Simulink对其进行了仿真，仿真结果验证了理论分析的正确性。

［1］ Kolar J W，Baumann M，Schgfmeister F.Novel Three-phase AC-DC-AC Sparse Matrix Converter［C］//Proceedings of 17th IEEE Applied Power Electronics Conferece and Exposi-tion，2002（2）：777-791.

［2］ 陈伯时.矩阵变换器的发展与展望［J］.电工技术杂志，2003（10）：4-5.

［3］ Wei Lixiang，Lipo T A.A Novel Matrix Converter Topology withSimpleCommutation［C］//Proceedingsof36thIEEEIndus-try Applications Society Conference，2001，13（3）：1749-1754.

［4］ 邓文浪，杨欣荣，朱建林，等.18开关双级矩阵变换器的空间失量调制策略及其仿真研究［J］.中国电机工程学报，2005，25（15）：84-90.

［5］ 王勇，文辉清，吕征宇，等.基于MATLAB的矩阵变换器空间相量调制研究［J］.电力系统及其自动化学报，2004，16（5）：14-19.

［6］ Mariethoz S，Wijekoont T，Wheeler P.Analysis Control and Comparison of Hybrid Two-stage Matrix Conberters for In-creasedVoltageTransferRatioandUnityPowerFactor［C］//Fourth Power Conversion Conference.Nagoya.Japan，2007：353-358.

［7］ 李志勇，蔡灏，李小颖，等.矩阵变换器的过调制策略及其仿真研究［J］.微计算机信息，2008，24（2）：282-284.

［8］ 李生民，闫晓飞，钟彦儒.混合式TSMC的改进与优化［J］.电力系统及其自动化学报，2011，23（3）：145-149.

［9］ 邓文浪，朱建林，张林亭.矩阵变换器空间矢量调制技术优化策略［J］.电工技术，2003，2（2）：27-29.

［10］周卫平，吴正国，唐劲松，等.SVPWM的等效算法及SVP-WM与SPWM的本质联系［J］.中国电机工程学报，2006，2（26）：133-137.

修改稿日期：2013-10-17

Simplified Modulation Method for Hybrid Two-stage Matrix Converter

XIONG Jian，HU Yan-kui，WANG Hong-hong，LI Qian-yu
（School of Automution&Electrical Engineering，Lanzhou Jiaotong University，Lanzhou730070，Gansu，China）

In order to solve the problem of complex control strategies and high voltage fluctuations of DC bus of hybrid TSMC ，for which a simplified method of pulse width modulation（PWM）was proposed in the rectifier stage.This method can simplify the calculation of duty and can make the rectifier stage to output direct voltage with constant average value in every switching cycle，and the SVPWM modulation method is convenient to be used in level inverter stage，so it contains the advantage of the conventional method.Finally，modeling and simulation was carried out in Matlab/Simullink to verify the correctness of the new modulation method.

hybrid two-stage matrix converter；rectifier stage；pulse width modulation（PWM）；duty cycle；modulation method

TM46

A

熊剑（1988-），男，在读硕士研究生，Email：524566800@qq.com

2013-08-15