关于逻辑语义学的句法系统

满海霞

一、引 言

逻辑语义学(又称形式语义学、语言逻辑)是逻辑学和语言学的交叉学科。它始于20世纪70年代初，以美国逻辑学家蒙太格(Montague)发表的The Proper Treatment of Quantification in Ordinary English为标志。逻辑语义学以自然语言的意义为研究对象，利用现代逻辑为其研究工具，探索复合表达式的意义如何由其组成部分的意义组合而来。这一核心思想，被称为组合原则①关于组合性原则的讨论，参见邹崇理《组合原则》，《逻辑学研究》2008年第1期。(Principle of Compositionality)。逻辑语义学还认为，语义不是孤立的，语义与句法之间具有同构关系，语义上由小到大的组合，与句法的组合方式也有关系。比如，在蒙太格语法(Montague Grammar)中，以上同构关系表现为一条句法规则匹配一条语义规则，因此，这一思想也被称为规则对规则假设。组合原则是逻辑语义学的核心法则。

对于自然语言来说，语义不如句法直观，它看不见、摸不着，不容易检验，所以通常情况下，对组合原则的探索除了借助语义推理运算，一个更重要的依据是它与句法间的同构关系。采取什么样的句法理论往往决定了语义系统的本质和刻画精度。在过去近半个世纪时间里，从“原创”句法规则(如蒙太格的PTQ系统)，到吸纳和借鉴当代句法理论的已有成果为己所用②B.Partee，Compositionality in Formal Semantics:Selected papers by Barbara H.Partee，Malden:Blackwell Publishing，2005;A.Kratzer，Modals and Conditionals，Oxford:Oxford University press，2012.，逻辑语义学家越来越关注当代句法学的理论成就。由于采用了更精致的句法系统，逻辑语义学对语义的生成愈加细致精准。

逻辑语义学借鉴的句法框架大致可分为转换生成语法和非转换生成语法两种。前者作为探索自然语言生成过程的机制非常成功，但是由于它将自然语言分为表层和底层，不适于只能看到表层字符串的机器进行语言处理。因此，计算语言学家构建了一批与转换生成语法生成力等价且不使用转换手段的单层结构语法。两类语法一个关照细琐的语言事实，一个照顾信息处理的需求，各有所长。本文将借助Heim＆Krater的语义系统和组合范畴语法CCG分别讨论在两类句法框架下如何实现句法和语义的平行推演，两种方法之间有何种转换关系，最后利用转换生成语法对表存在和完成的两类“有”的分析在CCG框架下做出统一的语义生成。

二、基于转换语法和非转换语法的逻辑语义系统

(一)Heim＆Kratzer的逻辑语义系统

在《生成语法的语义学》①I.Heim，A.Kratzer，Semantics in Generative Grammar，Oxford:Blackwell Publishers，1998.一书中，Heim＆Kratzer以转换语法的生成树结构为句法系统构建了一套外延语义系统，对修饰语、代词、量词等具体语言问题做了语义生成。该书对语义系统(以下简称HM语义系统)的构造方法基本成为本方向研究的公认做法。HM语义系统是蒙太格语法利用生成句法系统的延续，它首先定义句法树上终端节点成分的语义值，使得两个句法组成成分在毗连组成更大句法成分的同时，其语义值根据语义运算规则运算出更大句法成分的语义，直到得到语句的成真条件(truth－condition)，获得语句的意义②HM系统仍使用真值条件模型论的方法，认为句子的意义就是它的成真条件。其运算方式既可以从句法树的最底端向上逐步推进，也可以始自顶部，假设该句成真，向下将其化整为零，最后亦可同样得到成真条件。此处主要介绍自底向顶的做法，二者道理相同。。

在HM语义系统中，可能作为语义值的有:(1)a ∈De，De为个体的集合;(2)b ∈Dt，Dt为真值集合{0，1};(3)c∈DDte。对于句法树上的任意节点α，其语义值［|α|］是基于类型的λ－项，若α为终端节点，则［|α|］在词库中有定义。分叉树上的节点根据以下六条规则进行语义运算:

a.终端节点规则(TN):如果α是终端节点，则［|α|］为α在词库中的语义定义。

b.非终端节点规则(NN):如果α是非终端节点，β是其唯一子节点，则［|α|］ = ［|β|］。

c.函项应用规则(FA):如果α是二分叉树的母节点，{β，γ}是α的子节点集，且［|β|］是函项，［|β|］的定义域包含［|γ|］，则［|α|］ =［|β|］(［|γ|］)。

d.谓词修饰规则(PM):如果α是二分叉树的母节点，{β，γ}是α的子节点集，且［|β|］和［|γ|］都在 D〈e，t〉中，那么 ［|α|］ = λx.［|β |］(x)∧［|γ|］(x)。

e.语迹和代词规则(TP):如果α是代词或者语迹t，g是对变元的一个赋值，i在g的定义域中，则［|αi|］g=g(i)。

f.谓词抽象规则(PA):若α是二分叉树的母节点，它包含且仅包含β和γ为其子节点，如果β只统治数字索引标记i，那么，对于任何变元赋值 g，［|α|］g= λx. ［|γ|］ax/i。

用实例分析如下:

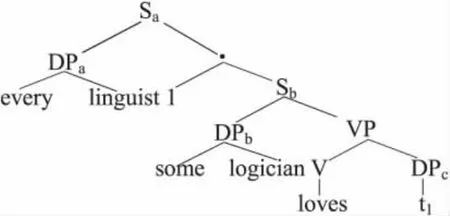
(1)是著名的量化歧义句，它有全称量词取宽域(对于每个语言学家，都有一位可能不同的逻辑学家喜欢他)和存在量词取宽域(存在至少一位逻辑学家，他喜欢每一位语言学家)两种解读，句法结构分别对应(2)和(3)。先看全称量词取宽域解读的生成。依据句法结构(2)、语义运算规则a－f和词库定义，Sa成真条件的具体演算过程如(4)所示。

(2)

(3)

因此得到(2)式解读的成真条件:∀z［linguist′(z)→ ∃x［logician ′(x)∧likes ′(z)(x)］］。类似的，依据句法树(3)，可以计算得到存在量词取宽域的成真条件为∃x［logician′(x)∧∀z［linguist′(z)→likes′(z)(x)］］，因为句法树(3)较(2)多了一次量词移位，所以依据(3)的语义运算过程需要多进行一次谓词抽象和一次针对语迹的变元赋值。

以上运算说明，利用转换生成语法作为句法系统计算自然语言语句的语义，优点大致有三:其一，转换生成树为二分叉结构，根据语义运算规则FA①HM系统中的其他规则从根本上讲也都遵守函项贴合思想，可以由FA规则直接或间接推得。比如PM规则实际是广义布尔合取规则的简化。关于广义布尔合取规则的讨论，参见B.Partee，R.Mats，Generalized Conjunction and Type Ambiguity，R.Bäuerle，C.Shwarze，von Stechow(eds.).Meaning，Use and Interpretation of Language，New York:Walter de Gruyter.1983.，同一母节点下的两个子节点在语义上一个是函项、一个是论元，使二分树直观地贯彻了语义的函项贴合思想，保证两个同级节点做句法毗连结合成更大句法单位的同时，其语义值做函项贴合运算生成相应的语义值。其二，转换生成语法将语句的句法结构分为表层结构②即直接成分结构。和深层结构，语句的语义解读由深层结构决定。这样一来，辖域歧义句(1)之所以有两种解读，是因为它在句法深层对应两个结构(2)和(3)，每种句法结构产生一种辖域解读。其三，转换生成语法对特定语言现象的句法解释，对语义生成也有所助益。例如，转换生成语法认为量词词组与普通名词短语不同，不能处在动词的论元位置，而需提升到S节点以上，并在其原来的论元位置上留下受到量词词组约束的语迹t③梅德明、杨春雷:《英语量词理论的对比研究》，《外国语》2002年第5期。，这种量词提升的操作在语义上解决了量词短语(语义类型为〈〈e，t〉，〈〈e，t〉，t〉④加类型的λ－项之间按照以下规则进行运算:(i)如果t1是类型为＜a，b＞的项，t2是类型为a的项，则t1(t2)是类型为b的项;(ii)如果t是类型为b的项，x是类型为a的变元，则λx.t的类型为＜a，b＞。)做宾语与谓语动词(类型为〈e，〈e，t〉〉)语义类型不匹配的问题。

毋庸置疑，基于转换生成语法思想探索意义的组合原则是从蒙太格系统中规则对规则操作向前迈进的一步，它对当代句法理论的选择性接受使得语义生成愈加精细。但是，从信息处理角度看，转换生成语法所提供的深层句法结构往往偏离语句的表层结构甚远，若要让只能看到表层字符串的计算机依据深层句法进行语句识别和语义生成，执行难度非同一般。计算语言学家关心的，是转换生成语法的描述和发现能否用非转换的语法表达出来，从而让机器可以直接通过语句的表层结构计算句子的句法甚至语义。出于这一思考，Steedman①A.Ades，M.Steedman，On The Order of Words，Linguistics and Philosophy，vol.4，no.4，1982;M.Steedman，Surface Structure and Interpretation，Cambridge MA:MIT Press.1996;M.Steedman，The Syntactic Process，Cambridge，Massachusetts:MIT Press.2000;M.Steedman，Scope taking:the Natural Semantics of Quantifiers，Cambridge＆ London:MIT press.2012.构造了与转换生成语法生成力相同、但不使用转换规则的单层语法——组合范畴语法CCG。②满海霞:《组合范畴语法与其计算特征》，《毕节学院学报》2013年第6期。

(二)单层语法CCG

CCG的理论基础是范畴语法，顾名思义，CCG句法将自然语言语词之间的毗连贴合体现为基于语词所对应范畴的推演运算。比如英语语句“John hits Mary”的CCG推演为(5)，其中“hits”的句法范畴(6a)与其两个论元分别依据向前(＞)和向后(＜)的范畴贴合规则做运算。我们将(5)自底部翻转过来，将每两个节点的结合过程转换成一个二分叉树，便得到类似(2)和(3)中的转换生成树。这种相似绝非偶然，而恰恰代表了改进早期形式句法分析理论—短语结构语法③直接成分分析法所对应的语法系统。它由一系列改写规则构成。比如(5)中语句的生成过程用短语结构语法可以表示为:S→NP VP;VP→V NP;NP→Det N。但是短语结构语法作为生成自然语言语句的语法，存在诸多缺陷与不足，见N.Chomsky，Three Models for The Description of Language，IRE Transactions on information theory 2，1956;N.Chomsky，Syntactic Structures，Berlin:Mouton，1957/2002。的那两条思路:转换方法与非转换方法。

(5)

利用非转换的手段获得类似转换操作的效果，方法大致有三:

其一，精细化范畴所带的信息。比如为“hit”的主语论元增加下标值agr代表“hit”的一致性特征，那么，hits的范畴就是(6b)。3S表示这个论元为第三人称单数，如果“hits Mary”碰到范畴为NP3S的John，则可生成合语法的句子，如果碰见范畴为NPPL的复数名词“the men”，生成过程停止。

其二，适当添加句法规则。表1是CCG向传统范畴语法中添加的三条组合规则。这三条组合规则是组合逻辑中对函项进行运算的三个语义组合算子的句法版本。有了这三条规则，CCG的句法规则直接保证生成转换生成语法需要借助移位、拷贝、删除等假设才能生成的非成分并列等无界依存现象，无须额外添加假设或者任何破坏表层句法结构的操作④关于这一点更详细的介绍，读者可以参阅Steedman(2000)，以及J.Baldridge，G.Kruijff，Multi－Modal Combinatory Categorial Grammar，Proceedings of 11th Annual Meetings of the European Association for Computational Linguistics，Budapest，2003.。

表1 CCG组合规则所对应的组合算子

(7)给定基本范畴集B，τ是从 CAT(B)到类型集TYPE的一个函数。τ是范畴到类型的对应函数当且仅当τ(AB)=τ(B/A)= 〈τ(A)，τ(B)〉。

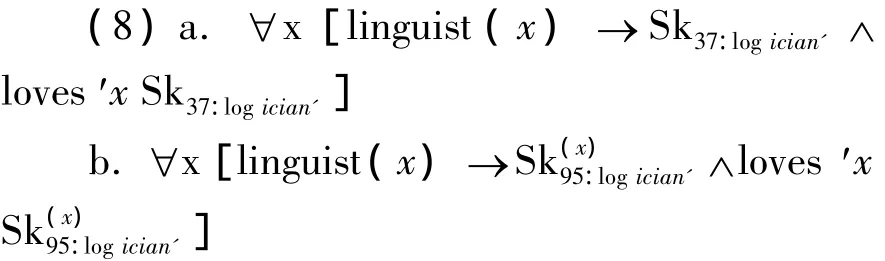
从以上三点可见，CCG突出体现了“小句法、大词库”的词汇主义特征，是典型的词汇主义语法。CCG之所以能够用单层结构实现等价于转换生成语法的生成力，词库的贡献功不可没。反过来，转换生成语法从句法角度的观察和发现，又是CCG对特殊词条做句法和语义赋值的思想源泉。以下我们将利用以上想法，尝试借助转换生成语法对汉语存在量词的探讨，构造汉语CCG的存在量化语义。

三、一点尝试——“有”的分析

最早讨论汉语如何表达逻辑量化的可能是赵元任先生，他在Notes on Chinese Grammar and Logic①Y.Chao，Notes on Chinese Grammar and Logic，Philosophy East and West，vol.5，no.1，1955.中敏锐地注意到，汉语不像英语，没有专职的量化限定词②他称之为量化形容词，如英语中有“SOME/A”和“ALL”。，若要表达逻辑中“存在至少一个 x满足x具有性质φ(即∃x φ(x))”的概念，英语中可以说“SOME logician loves Mary”，汉语中最近似的表达是“有位逻辑学家喜欢玛丽”。“有”存在量化力量在汉语学界基本得到了共识③沈家煊:《词序与辖域——英汉比较》，《语言教学与研究》1985年第1期;陈宗明(主编):《汉语逻辑概论》，北京:人民出版社，1993;吴平:《量化词辖域歧义在Prolog语言中的消歧方案》，《外语与外语教学》2004年第12期;吴平:《汉语量化句的逻辑语义分析与计算》，《湖南科技大学学报(社会科学版)》2007年第1期。，但是“有”不如“some”单纯，它除了表存在量化，至少还兼表另两个重要的概念——“存在”和“拥有”。袁毓林等人④袁毓林、李湘、曹宏等:《‘有’字句的情景语义分析》，《世界汉语教学》2009年第3期。通过对大量语料的分类分析，发现“有”的各种意义之间紧密相关，表存在量化的“有”是其存在和拥有含义彻底虚化的结果，它将其后无定性成分转变成话题。转换生成语法则从句法深层结构解读了这类“有”与表完成貌的“有”之间的关系。黄正德⑤黄正德:《说‘是’和‘有’》，《中研院史语所集刊》1988年第59本第1分册。指出，“有”的三种用法格局(9)中，除了a格局中典型的动词领属用法，表完成貌的b格局和表存在的c格局在深层句法结构上都是一个以子句为宾语的无主句结构(10a)。不同的是，b中的主语可以经过提升移到母句的主语位置，呈(10b)形式，c格局因为汉语中主语倾向于有定，主语“一个人”作为无定名词组不能提升，因此留在原位，参见(10c)。

(9)a.主语…有…宾语(他们有很多钱。)

b.主语…有…谓语(张三没有看见李四。)

c.有…主语…谓语(有一本书放在桌子上。)

(10)

b、c两个格局虽在表面上作完成句和存在句之分，语义上实际都表示一种存在量化，完成句意指事件或者动作的存在，存在句指人或物的存在。从句法的角度解释，b格局因为主语未提升，“有”后接主语，因而表示主语的存在;而c格局的主语被提升，“有”后接谓语，因而表示谓语所指涉事件的存在，即动作的完成。从语义的角度解释，c中“有”与其后主语结合，类似英语存在量词，断定存在至少一个这样的个体具有谓词所描述的性质，b中“有”与其后谓语结合，断定存在至少一个这样的性质。将此对助动词“有”的句法、语义分析结果分别转化为CCG的句法范畴和语义λ－项，可以得到“有”的两个赋值(11a－b):

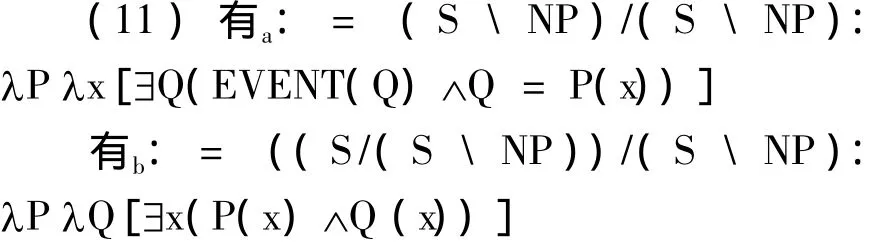
由此对(9b－c)中两句分别进行CCG的句法语义推演(12a－b)①因(12b)中的“一个人”在语义上无定指，相当于一个通名，而本文并没有区分专名和通名(即NP与N)，所以我们采纳蒙太格语法的做法，认为通名与不及物动词短语都表示性质的集合，对应句法范畴为(SNP)。虽然两句中“(没)有”的表层句法位置不同，但我们最后计算得到的语义真值条件都是存在式，一个表示动词短语所表示的事件Q的存在，一个表示主语个体x的存在。

四、结 语

在逻辑语义学探索语义组合原则的旅程中，句法理论的选择往往决定了语义生成的精准程度。纵观逻辑语义学的发展历程，借助成熟的句法理论来发展语义的趋势越来越突出，这些句法理论若溯本逐源，都可以归到乔姆斯基的转换生成语法。所以，目前我们亟须解决的问题，就是如何将转换生成语法的句法成果转化为适合逻辑语义构造的句法机制，使其切切实实地为语义服务。Heim、Kratzer等人在生成树上构造的语义系统、Steedman在CCG框架下进行的词汇主义转换以及我们对助动词“有”的讨论都是这方面有益的尝试。

责任编校:徐玲英