基于ARMA－GARCH类模型的SHIBOR的VaR比较

何晓光 黄德权

(广东财经大学金融学院，广东 广州 510320)

一、引言

作为巴塞尔协议的成员国之一，我国商业银行面对的是全球银行的全面开放及经营模式的国际接轨，随着我国利率市场化改革的不断加快，利率将更多地受到市场规律的影响，中国经济慷慨分享到了利率政策带来的巨大红利;另一方面，利率市场化改革无疑也会给商业银行及工商企业带来一定程度的风险，以同业拆借利率为例，在市场化以后，利率波动增大，商业银行在同业拆借市场上的交易量逐年增加，使得商业银行的同业拆借头寸面临巨大的利率风险。

在我国利率市场化改革的进程中，传统的利率敏感性缺口分析方法和持续缺口分析方法的缺陷将越来越不能满足现代商业银行利率风险度量的要求。VaR方法在金融监管中具有重要的地位和作用，因为巴塞尔委员会将VaR模型定为商业银行利率风险管理的基本工具，使得VaR模型被许多国家的金融当局作为风险测量的一种工具，得到了广泛地推广，我国金融业需要接受国际化的风险管理模式，引入先进的风险管理VaR方法，对同业拆借利率的波动进行监测，并合理地估计与控制同业拆借头寸所面临的利率风险可称为当务之急。中国人民银行也可以通过运用VaR模型对各金融机构进行监管，商业银行则可以提高内部风险管理的技术水平。国内外应用VaR方法进行金融风险管理的研究较多，Ricardo(2006)［1］、Beirne 等(2010)［2］分别采用GARCH模型对VaR进行预测;李成和马国校(2007)［3］认为t分布不适合描述我国银行间同业拆借利率序列的分布状况，GED分布能较好刻画我国银行间同业拆借利率序列的分布;王德全(2009)［4］认为t－分布和g－分布下的模型能更好地捕捉我国银行间质押式回购市场利率序列的尖峰厚尾性;杨娴等(2011)［5］利用多种方法建立了国际有色金属期货市场风险的 VaR模型;侯外林(2011)［6］将ARMA模型与GARCH模型相结合，测算股指年度收益率的VaR值，对股指的波动以及相伴概率进行了预测;张海波和陈红(2012)［7］认为我国人民币兑美元市场具备使用VaR模型度量人民币汇率波动风险的条件，并且人民币兑美元的汇率风险随着持有期的增大而增大;严伟祥和张杰(2013)［8］基于GARCH模型来预测对冲基金日交易波动率并估算在险价值(VaR);李良松(2009)［9］通过研究上海同业拆借利率的市场风险，认为条件异方差模型计算的VaR过于保守;房小定和吕鹏(2013)［10］利用VaR模型对上海同业拆借利率进行度量，认为GED分布较好地刻画了SHIBOR对数日收益率序列的分布。

对于以上的研究:笔者认为有以下几点值得进一步讨论:(1)国内同行研究者多采用CHIBOR作为研究对象，CHIBOR由于形成机制的问题难以全面反映我国货币市场的资金供求情况，而SHIBOR一般被认为是中国短期基准利率的代表。(2)国内同行数据一般较早，不能全面反映市场的发展情况，且多研究的是隔夜同业拆借利率数据，而金融机构以1W及1M为参考利率的交易量也非常大。(3)少数研究使用利率数据而不是其收益率数据建立模型，准确性值得商榷，同时研究空头与多头头寸的相对VaR模型的也较少。基于以上因素，拟选择SHIBOR的周数据和月数据，区间为2007年1月4日至2013年 12月 31日，分别建立 ARMA—EGARCH(TARCH，PARCH)空头及多头头寸相对VaR模型。

二、理论模型

(一)GARCH模型簇

Pagan和 Schwert(1990)［11］以及 Nelson(1991)［12］把标准残差作为方差方程的移动平均的回归因子，提出了EGARCH模型，能够刻画许多金融时间序列中的波动非对称性特征，其形式是:

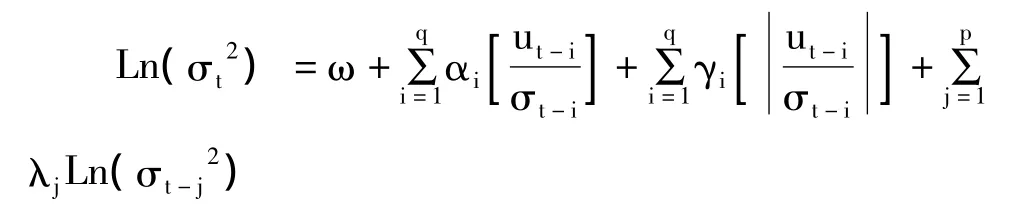
等式左边是条件方差的对数，这意味着杠杆影响是指数的，而不是二次的，等式右边第3项是标准新息的绝对值，该项可以区别正、负新息对波动的不同影响，杠杆效应的存在能够通过γ＜0的假设得到检验，如果γ≠0，则冲击的影响存在着非对称性。

由于标准差的GARCH模型模拟的不是方差，而是标准差，因此大幅度的冲击对条件方差的影响比在标准差的GARCH模型中要小，基于这种思想，Ding等(1993)［13］提出了 PARCH 模型，形式为:

其中，δ ＞0，当 i=1，2，…，r时，|γi|≤1;当 i＞ r时，γi=0，r≤p。在PARCH模型中，标准差的幂参数δ是估计的，捕捉冲击对条件方差的影响幅度，而γ是捕捉直到r阶的非对称效应的参数，γi=0表示不存在非对称效应。

Glosten 等(1994)［14］以及 Zakaran(1994)［15］提出TARCH模型，高阶的TARCH模型形式如下:

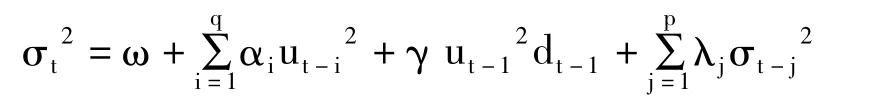
当ut－1＜0 时，dt=1;否则，dt=0称为非对称效应项，好消息(ut－1＞0)和坏消息(ut－1＜0)对条件方差有不同的影响:只要γ≠0，条件方差对冲击的反应是非对称的，如果γ＞0，我们说存在杠杆效应，非对称效应的主要效果是使得波动加大;如果γ＜0，则非对称效应的作用是使得波动减小。

CARCH模型是GARCH模型的扩展形式，CARCH(1，1)是一个非线性的严格的 GARCH(2，2)模型，能够描述波动的短期和长期特征:

第一个方程称作短期分量方程，其中σt2仍表示波动，qt表示随时间变化的长期波动，σt2－qt将以速度(α1+γ)趋近于零。第二个方程称作长期分量方程，其中ω是常数，qt将以速度λ1收敛于ω，其中 z是外生变量，d 是哑变量，当 ut－1＜0 时，dt=1，否则，dt=0;γ＞0意味着条件方差中的暂时杠杆效应。

(二)VaR的计算

参数方法是计算VaR，首先需假设收益率服从一定的分布，由于SHIBOR的收益率序列的概率分布较难确定，常用GARCH模型估计波动率，当置信水平为c，资产持有期标准化后，就可以求得VaR值，根据相对VaR的计算方法，可得资产持有者的多头头寸和空头头寸的相对VaR值分布为:

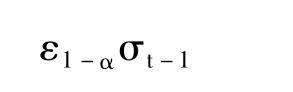
Pt－1、σt－1分别为 SHIBOR 的收益率拟合模型的条件均值和条件方差的向前一步预测值，εα、ε1－α分别为ε分布的左尾和右尾α分位数。

(三)关于分布

GARCH模型簇中的残差分布通常有正态分布、t－分布和广义误差分布(GED)，当正态分布不足以反映收益率序列的特性时，可以采用 Nelson和Hamilton等人提出的t－分布和GED分布来拟合，GED分布的概率密度函数为:

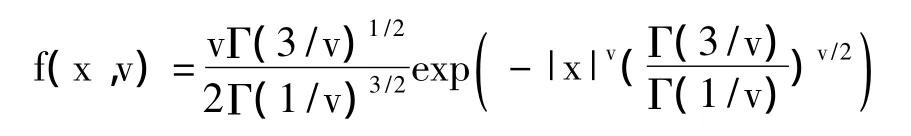
当v＜2时，GED表现为厚尾;当v=2时，GED为正态分布;当v＞2时，GED则表现为瘦尾。

三、数据的基本特征

CHIBOR是实盘交易形成的利率，而SHIBOR是报出的利率，这是两者的一个很大区别，CHIBOR是以各银行同业拆借实际交易利率的加权平均值来确定，拆借依赖于交易者的信用，且拆借市场交易规模小和活跃性低，而SHIBOR是由信用等级较高的银行组成报价团自主报出的人民币同业拆借利率确定的算术平均利率，可以认为是剥离了信用升贴水后的利率，信息的披露也相对充分，能够更合理解释我国银行在同业拆借市场上所面临的利率风险，2007年1月4日上海银行间同业拆借市场正式运行，选择SHIBOR的1W和1M作为研究样本，数据区间为2007年1月4日至2013年12月31日。

(一)样本数据的处理

为得到平稳收益率时间序列，对SHIBOR数据分别计算了复合收益率，即SHIBOR的自然对数日收益率，Rt=lnSHIBORt－ lnSHIBORt－1，通过对数收益率的处理可以有效地消除原数列的自相关性。

(二)对Rt序列的检验

观察1W和1M数据序列的Rt曲线图，发现收益率序列没有明显的趋势部分，且呈现波动的异方差性。在运用Rt计算商业银行的同业拆借头寸的风险价值VaR时，为了合理选择模型，我们对SHIBOR及Rt序列进行了正态性检验、平稳性检验、自相关性及条件异方差性检验。

1.SHIBOR和Rt分布与正态分布有偏差。SHIBOR的1W和1M从2007年到2013年的平均值分别为 2.949%、3.531%，标准差分别为1.375%，1.534%。SHIBOR的1W和1M数据分布呈现非对称性与右偏倚，而二者的收益率Rt分布峭度显著大于3且呈现左偏倚。

2.SHIBOR和Rt序列相关性特征不同。SHIBOR的1W和1M数据序列自相关图呈现缓慢衰减特性，偏自相关图都呈现一阶截尾。而图2中反映的收益序列的1－15期自相关函数和偏自相关函数值，均存在较弱的自相关现象。

3.SHIBOR和Rt平稳性不同。平稳性检验方法主要有非参数检、自相关检验以及单位根检验，SHIBOR的1W和1M数据序列不平稳，收益序列Rt序列都平稳，通过运用LM检验，证实Rt序列是自回归条件异方差过程。

综合上述分析，采用ARMA与GARCH类模型来估计和预测同业拆借利率的波动性特征。

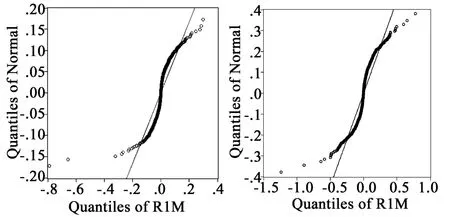
图1 上海同业拆借利率1W和1M的收益率序列的正态Q－Q图

四、实证分析与模型检验

(一)各种分布假设下 Rt的 ARMA－GARCH模型簇估计

对序列R1W和R1M，分别假定模型残差序列服从n－分布、t－分布和g－分布，基于AIC、SC值及残差检验，并考虑模型系数的显著性水平，确定模型滞后阶数。

经过反复测算，最终为R1W序列和R1M分别选择了7种刻画其时变性特征的条件异方差模型，具体优选模型见表1，具体拟合参数见表2，表3。

图2 上海同业拆借利率1W和1M的收益率序列相关图

表1 收益率序列和在不同分布假设下的优选模型

表2 上海同业拆借利率1W的收益率序列拟合结果

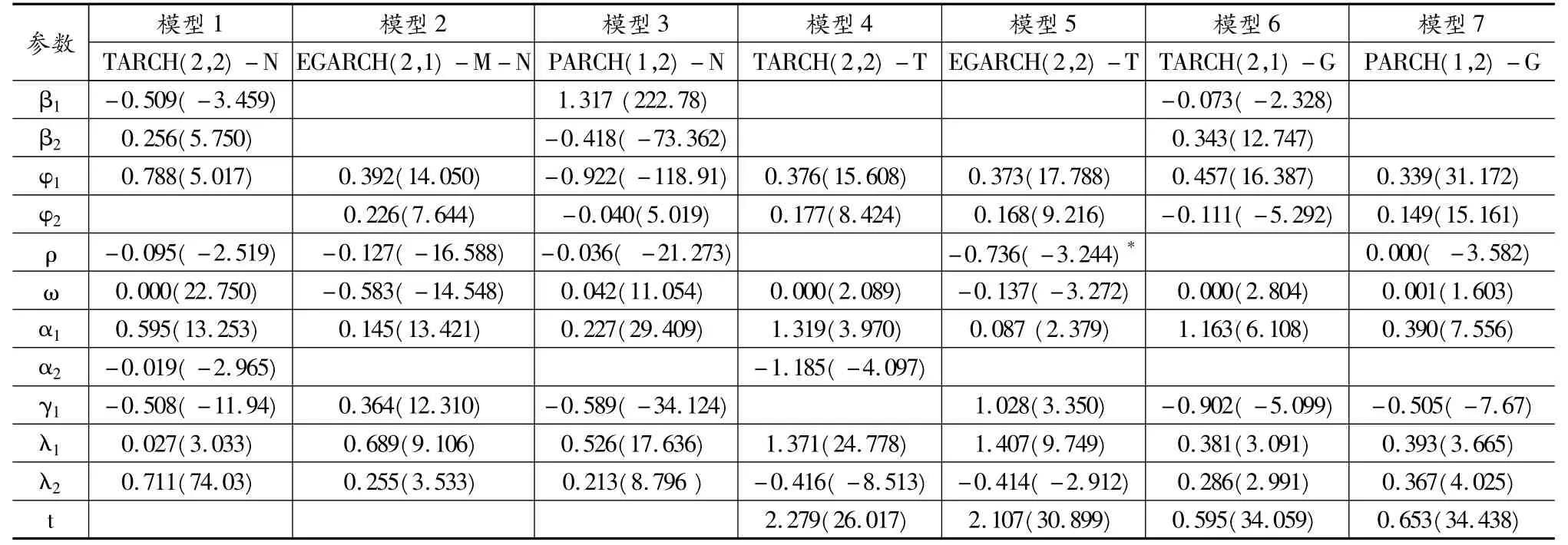
表3 上海同业拆借利率1M的收益率序列拟合结果

从表2，表3各模型估计参数来看，参数均在5%的显著性水平下显著。对估计残差分别做异方差效应的LM检验，发现不存在显著的异方差现象，所以上述各模型能够较好地反映了收益率序列的异方差现象。从各模型的均值方程的形式基本一致可以看出，SHIBOR的1W、1M数据序列的变化分别与其前三期、前二期的变化有较大的关系。各收益序列都有六个模型的参数γ1估计值是显著的，可以认定收益率R1W和R1M存在波动的非对称性特征。值得注意的是，R1W和R1M各个估计模型中，EGARCH模型估计的参数 γ1都是大于 0的，PARCH和TARCH模型估计的参数γ1都是小于0的，说明了R1W和R1M波动的非对称性特征表现为反杠杆效应特征，即表现为利率向上变动时带来的波动幅度大于利率向下变动时的波动幅度。

(二)VaR模型的回测检验

通过上述拟合的GARCH模型簇，在不同的分布及置信度下，计算出上海同业拆借利率市场VaR结果，所构建的VaR模型是否有效，需要采用回测技术来检验VaR模型的准确性。采用的回测检验方法是由Kupiec(1995)提出的基于失效率的似然比率验证方法，检验统计量为:

在零假设成立条件下，统计量LR服从自由度为1的卡方分布，其95%置信水平下的分位数为3.841，当在95%置信水平下计算VaR时，如果此时的LR＞3.841，我们就拒绝模型，在置信度为95%时，预期理论失败天数为1745*5%=85天。

从表4的研究结果可知:对SHIBOR的1W数据而言，在相同新息分布假设和相同的显著性水平下，基于正态分布和GED分布假设下，各模型计算得到的多头头寸和空头头寸的VaR估计失败天数无明显差异;这两种分布都稍稍高估了多头头寸的风险，同时低估了空头头寸的风险，相对而言，对多头头寸的估计更接近真实值。LR统计量的值越小，越无法拒绝VaR模型的正确的原假设，说明该模型的预测越准确，从LR统计量可知，在95%的置信水平下，基于正态分布的模型3:PARCH(2，2)－N和基于GED分布的模型7:EGARCH(2，1)－M－G，比较接近临界值，说明了这两个模型较近似的估计了多头头寸的VaR值。而基于t分布假设的估计大大高估了市场风险，不适合作为SHIBOR的1W序列的风险估计。

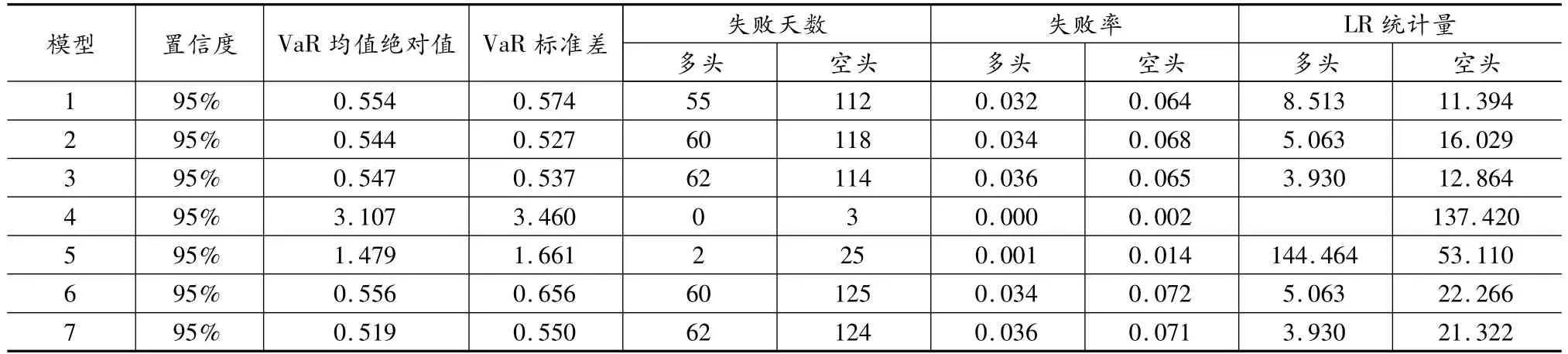
表4 置信度为95%的各模型1W相对VaR的统计结果

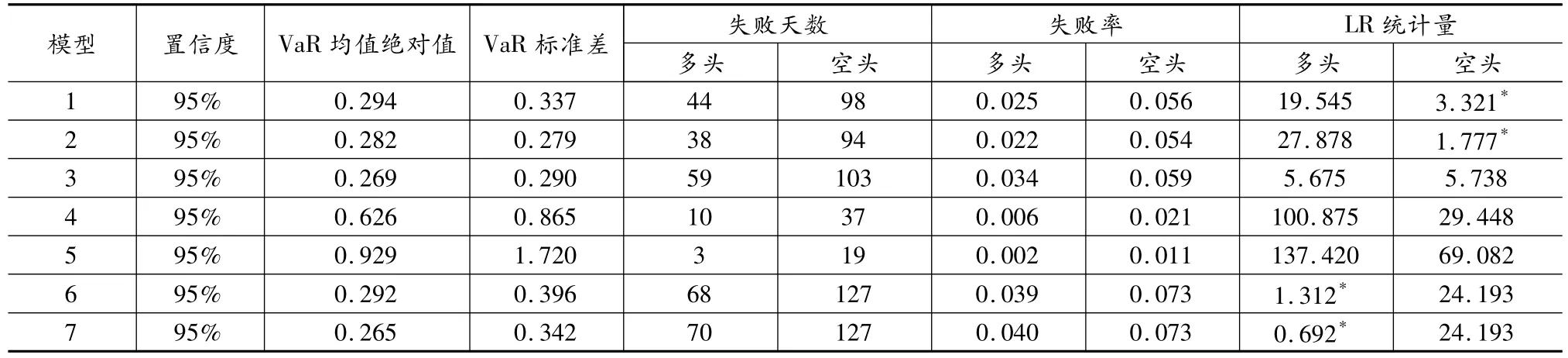
表5 置信度为95%的各模型1M相对VaR的统计结果

表5的研究结果表明:对SHIBOR的1M数据而言，在相同新息分布假设和相同的显著性水平下，各模型计算得到的多头头寸和空头头寸的VaR估计失败天数差异不大;从LR统计量可知，基于GED分布的多头头寸VaR估计的模型6和模型7，在95%的置信水平下，通过了显著性检验，说明了GED分布假设可以准确地估计多头头寸的风险;同理，基于正态分布的模型1和模型2也通过了显著性检验，说明了基于正态分布的假设可以准确地估计空头头寸的风险;无论是对多头头寸还是空头头寸，基于t分布假设的估计都大大高估了市场风险，不适合作为SHIBOR的1M序列的风险估计。

五、结论

通过建立基于不同分布假设下的ARMAGARCH模型簇的相对VaR模型，实证分析上海同业拆借市场的利率风险，得出如下结论:

第一，通过选择适当的滞后阶数和新息假设，上海同业拆借市场收益序列可以通过ARMAGARCH模型簇来刻画，对于SHIBOR的1W数据而言，基于正态分布和GED分布假设，都稍稍高估了多头头寸的风险，同时低估了空头头寸的风险，相对而言，对多头头寸的估计更接近真实值，而基于t分布假设的估计大大高估了市场风险，不适合作为SHIBOR的1W序列的风险估计。

第二，对SHIBOR的1M数据而言，GED分布假设可以准确地估计多头头寸的风险;基于正态分布的假设也能够准确估计空头头寸的风险;无论是对多头头寸还是空头头寸，基于t分布假设的估计都倾向高估市场风险。

第三，分布假设和显著性水平的高低影响VaR值的准确性。在新息相同分布假设和相同的显著性水平下，不同的GARCH类模型计算得到的VaR值并无明显差异，失败天数相差不大，而在不同分布假设和不同的显著性水平下，返回测试的结果却出现了明显的差异。说明模型种类的选择并非VaR值度量的关键因素，而VaR更关注尾部特征。另外，对于1W和1M两种数据，正态分布新息假设都倾向于高估多头头寸的风险值，过于保守和悲观，而GED新息假设都倾向于低估空头头寸的风险值，又显得过于乐观。

［1］Ricardo A.The Estimation of Market VaR Using GARCH Models and a Heavy Tail Distribution［R］.Working Paper Series.2006.

［2］Beirne，Caporale，Ghattas，et al.Global and regional spillovers in emerging stock markets:A multivariate GARCH－in－mean analysis? ［J］.Emerging Markets Review，September 2010，11，(03):250 －260.

［3］李成，马国校.VaR模型在我国银行同业拆借市场中的应用研究［J］.金融研究，2007，(05):62－77.

［4］王德全.质押式回购利率的风险度量研究——基于ARMA－GARCH 模型的实证检验［J］.财经研究，2009，(08):15－25.

［5］杨娴，陆凤彬，汪寿阳.国际有色金属期货市场VaR和ES风险度量功效的比较［J］.系统工程理论与实践，2011，(09):1645－1651.

［6］张海波，陈红.人民币汇率风险度量研究——基于不同持有期的VaR分析［J］.宏观经济研究，2012，(12):25－31.

［7］严伟祥，张杰.基于GARCH－VaR模型的对冲基金市场风险度量研究［J］.经济与管理评论，2013，(05):78－83.

［8］李良松.上海银行间同业拆借利率VaR的有效性研究［J］.金融研究，2009，(09):110－122.

［9］房小定，吕鹏.基于GARCH模型的上海同业拆借利率风险度量［J］.西安电子科技大学学报，2013，(04):18－26.

［10］Pagan，Adrian，Schwert.William，Alternative Models for Conditional Stock Volatility［R］.NBER Working Paper No.w2955.October1990.Available at SSRN:http://ssrn.com/abstract=461388.

［11］Nelson DB.Conditional heteroskedasticity in asset returns:A new approach［J］.Econometric a，1991，(59):347 －370.

［12］Ding，Granger，Engle.A Long Memory Property of Stock Market Returns and a New Model［J］.Journal of Empirical Finance ，1993，(02):83 －106.

［13］Glosten，Jagannathan，Runkle.On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks［J］.Journal of Finance，1993，(48):1779－1801.

［14］Zakoian JM.Threshold Heteroskedastic Models［J］.Journal of Economic Dynamics ＆Control，1994，(18):931 －995.