Fast SSED-MoM/FEM Analysis for Electromagnetic Scattering of Large-Scale Periodic Dielectric Structures＊

He Xiaoxiang(何小祥)，Liu Chen(刘辰)，Yang Yang(杨阳)

College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China

1 Introduction

Periodic structures such as phased-array antenna［1］，frequency selective surfaces(FSS)［2］and electromagnetic band-gap(EBG)structures［3］have been widely used and intensively investigated in the electromagnetic engineering for decades.Hence，accurate and efficient electromagnetic simulation techniques are essential for the design of periodic structures.Among the full-wave analysis techniques，the method of moment［4］(MoM)is a popular approach to deal with electromagnetic scattering of periodic structures.However，the conventional MoM requires O(N2)memory and O(N3)computational complexity，which are unaffordable for large-scale problems with desired accuracy.The other full-wave methods such as the finite element method(FEM)［5］and the finite difference time domain method(FDTD)［6］are also expensive for large-scale analysis on current state-of-the-art personal computers.

The sub-entire domain(SED)basis function is an approach to reduce the memory requirement.An accurate sub-entire domain(ASED)basis function method［7］is proposed for scattering analysis of periodic structures consisting of metal elements and a simplified sub-entire domain(SSED)basis function method is proposed，in which the mutual coupling among the elements is directly neglected while computing the basis function and it is thus shared by all the elements.According to the characteristic of periodic structures，an extended SED basis function method［8］is proposed to further reduce the number of unknowns.Although the unknowns are reduced with SED-MoM，the conventional MoM is not ideal for simulating complex dielectric composite objects due to the difficulty in acquiring the SED basis function on each single cell.In this case，a novel SSED-MoM/FEM hybrid method which is capable of handling complex-dielectric-composed elements is proposed.However，it is still time-consuming when computing large-scale periodic structures with SSED-MoM/FEM method.

In this paper，an accelerated SSED-MoM/FEM method is proposed to analyse large-scale periodic structures.The number of unknowns is dramatically reduced with non-uniform mesh according to the total field-scattered field splitting technique in FEM.With all elements share the same SSED basis function，conjugate gradient-fast Fourier transform［9］(CG-FFT)can be performed in the whole periodic structure.To further improve the computational efficiency，OpenMP［10］parallel technique is employed.

2 Formulation

Consider a two-dimensional(2D)planar periodic structure consisting of N0=NxNyelements that are arranged in the xoy plane in free space，as shown in Fig.1.Here，Nxand Nyare the numbers of cells along the x and y axes.

Fig.1 Periodic structure with a finite size of N0=Nx×Ny

2.1 Finite element formulation with non-uniform mesh

For the analysis of one element，the whole domain is split into total field and scattered field by the connecting boundary which is referred from that of the finite difference time domain method［11］，as shown in Fig.2.Only 0.1λ edge size mesh is needed to ensure the accuracy of followed SSED-MoM.With the application of non-uniform mesh，the object is meshed with 0.05λ or even less and the mesh size of other parts is about 0.1λ.Take 0.5λ ×0.5λ ×0.05λ plate for example，it creates 57 457 elements with uniform mesh(0.05λ).However，by using non-uniform mesh，there are only 9 387 elements generated.

Fig.2 Boundary definition and non-uniform meshes of total-and scattered-field

Equivalent function can be acquired with traditional finite elements procedure.The electric field and magnetic field on the output boundary(OB)surface can be obtained as the SSED basis function.

where Niis the interpolation basis function，αithe corresponding coefficient and M the total number of triangular meshes on OB surface.With the application of non-uniform mesh，the unknowns of FEM is decreased evidently，as well as the computational complexity of SSED-MoM.

2.2 CG-FFT accelerated SSED-MoM formulation

For periodic structures，the field on artificial closed surface Sn(nth cell)consists of incident field Ei/Hi，scattered field Es/Hsof its own and coupling Ec/Hcfrom other elements.After using Galerkin's procedure and SSED basis functions，the whole interaction of periodic structure can be expressed in a matrix equation combing electric field integral equation(EFIE)with magnetic filed integral equation(MFIE)

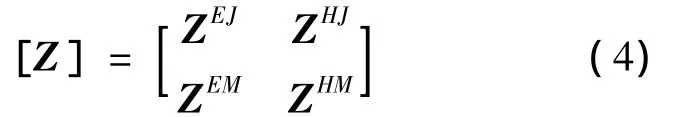
where ZEJis the electric field-electric current sub-matrix，ZHJthe magnetic field-electric current sub-matrix，ZEMthe electric field-magnetic field sub-matrix，and ZHMthe magnetic field-magnetic current sub-matrix.The matrix in Eq.(4)involves 2N0unknowns and requires O(4)memory to store a dense matrix equation，which is relatively expensive.The computational complexity is O((2N0M)2).Although matrix［Z］does not satisfy the Toeplitz characteristic，each of the four parts satisfies the characteristic due to the periodic nature of the structure and the use of unique SSED basis function.Then the matrix-vector multiplication can be performed efficiently using the FFT technique individually.

The matrix representing EFIE and MFIE can be written as

In the global Cartesian coordinate system，the distance vector can be expressed as

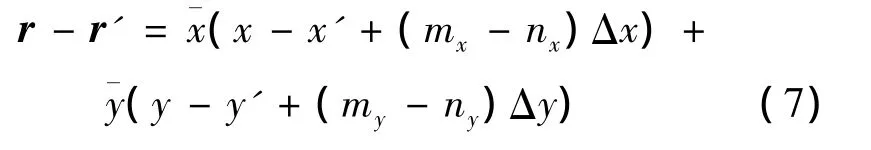
where(x'，y')and(x，y)are the coordinates of the observation cell Snand source cell Sm.Δx and Δy are the gaps in the x and y directions between two unit cells.Then one gets

Hence，the matrix equations can be rewritten as

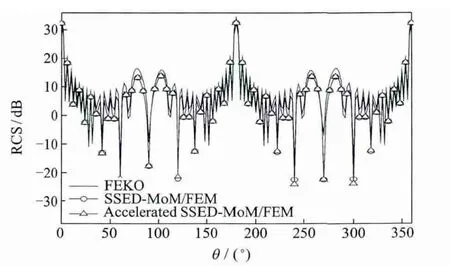
Fig.3 Bistatic RCSs of 15×15 dielectric plate array in normal incidence case

After using the discrete Fourier transform(DFT)，Eqs.(9，10)can be written as

where F－1is the Fourier transformation(in0)is the DFT of Zs(mn0)，and~β(in0)the DFT of coefficient β(mn0).

Due to the application of CG-FFT，only 2N0matrix elements are needed to be computed and stored.Therefore，the computational complexity of matrixvector multiplication is reduced to O(2MN0log(2N0)).The computational efficiency has been greatly improved.

2.3 Application of OpenMP technique

In order to take full advantages of computer resources and improve computational efficiency，OpenMP technique is applied to SSED-MoM/FEM method.Assuming that the time cost of parallel regions is Tpand that of the other part Ts，the computation time is Ts+nTpwith serial computing in theory，where n denotes the number of threads.The speed-up ratio can be written as(Ts+nTp)/(Ts+Tp).

3 Numerical Results and Discussion

The results are computed by a personal computer with Intel(R)Core(TM)2 Quad CPU Q8200-2.33 GHz and 4 GB RAM.

3.1 Dielectric plate

Fig.3 shows the bistatic RCSs of a 15×15 array consisting of dielectric plates in normal incidence case.The permittivity of dielectric is 2.5，the size of plate is 0.5λ ×0.5λ ×0.05λ and the gap is 0.5λ.The SSED basis function is calculated by FEM with non-uniform mesh and the unknowns are decreased to one sixth.The computation will spend 1 681.84 s for a uniform mesh and 110.78 s for a non-uniform mesh.Furthermore，only 544 triangles are produced on the OB surface with non-uniform mesh while for the one with one with uniform mesh，the number of triangles increases to 1 920.After applying the three techniques， the computation time decreases to 7.05 min.The computation time of 5×5，10×10，15×15，20×20 arrays consisting of associated elements is presented in Table 1.For the 20×20 array，the speedup ratio is up to 3 031.

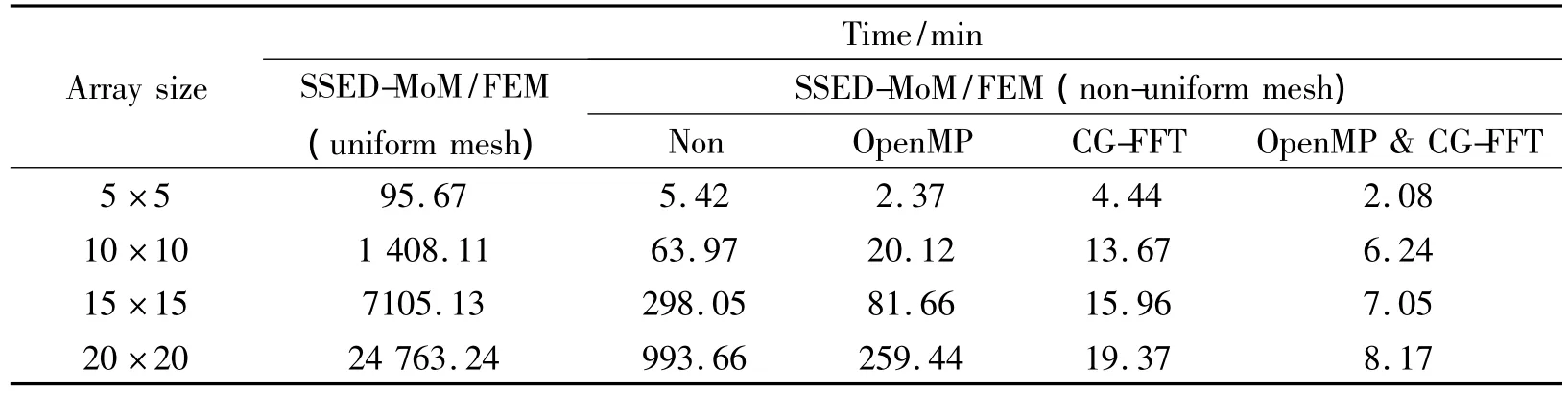
Table 1 Comparison of CPU time

3.2 Microstrip patch antenna

To test the new method for analyzing complex dielectric-composite object，we analyse the array consisting of microstrip patch antennas.The permittivity of the dielectric substrate is 2.5.Fig.4 illustrates the dimension of the antenna and the bistatic RCSs of the 15×15 array calculated at 300 MHz.Only 710 triangles on the OB surface are created compared to 2 594 triangles with uniform mesh.The time for calculating SSED basis function reduces from 10 519.61 s to 298.50 s with non-uniform mesh.

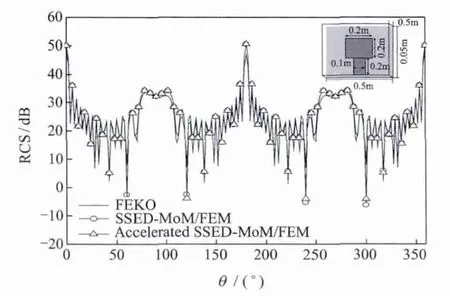
Fig.4 Bistatic RCSs of 15×15 patch antenna array in normal incidence case

In order to further discuss the effect of CG-FFT，the speed-up ratio of the SSED-MoM part is calculated.Table 2 illustrates the speed-up ratios of the two models.The speed-up ratio of CG-FFT part is mainly decided by the structure scale and the number of triangular meshes on the OB surface.With the expansion of array scale，the advantages of our accelerated method will be more evident.

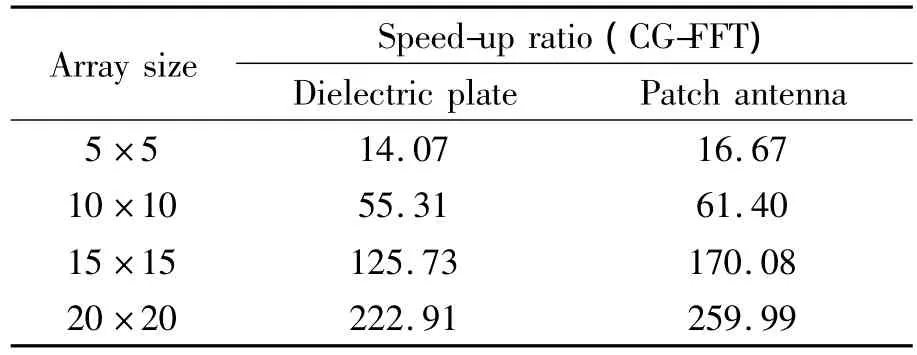
Table 2 Comparison of speed-up ratio

Usually，it is difficult to analyse the electromagnetic scattering of microstrip patch antenna array in its bandwidth，especially at the resonant frequency for the oscillation of radiator.Fig.5 shows the bistatic RCSs calculated at resonant frequency 510 MHz.The results further validate that the accelerated method is in excellent accuracy.The speed-up ratio of SSEDMoM procedure after applying CG-FFT is 177.63.

Fig.5 Bistatic RCSs of 15×15 patch antenna array at resonant frequency

4 Conclusions

An accelerated hybrid SSED-MoM/FEM method is proposed to analyse large-scale periodic structures.By using non-uniform mesh，the unknowns have been reduced sharply.And then CPU time drops obviously with the application of CG-FFT and OpenMP.Some numerical results are shown to verify the efficiency and accuracy of our accelerated method.

［1］ He Q Q，He H D.An efficient pattern synthesis method for cylindrical phased array antennas［J］.Journal of E-lectromagnetic Waves and Applications，2009，23(4):473-482.

［2］ Zareian-Jahromi E，Khalilpour J.Analysis of a freestanding frequency selective surface loaded with a nonlinear element［J］.Journal of Electromagnetic Waves and Applications，2011，25(2-3):247-255.

［3］ Li H，He X X.Bandstop characteristic of light reflection from morpho butterfly’s wing［J］.Journal of Electromagnetic Waves and Applications，2008，22:1829-1838.

［4］ Bozzi M，Perregrini L.Analysis of multilayered printed frequency selective surfaces by the MoM/BI-RME method［J］.IEEE Trans Antennas Propag，2003，51:2830-2836.

［5］ Cai Y，Mias C.Faster 3D finite element time domainfloquet absorbing boundary condition modeling using recursive convolution and vector fitting［J］.IET Microwave，Antenna＆Propag，2009，3(2):310-324.

［6］ Li D Y，Sarris C D.A new approach for the FDTD modeling of antenna over periodic structures［J］.IEEE Trans Antennas Propag，2011，59(1):310-314.

［7］ Lu W B，Cui T J，Qian Z G，et al.Accurate analysis of large-scale periodic structures using an efficient sub-entire-domain basis function method［J］.IEEE Trans Antennas Propag，2004，52(11):3078-3085.

［8］ Du P，Wang B Z，Li H.An extended sub-entire domain basis function method for finite periodic structures［J］.IEEE Antennasand WirelessPropagation Letters，2008，7:404-407.

［9］ Lu W B，Cui T J，Yin X Y，et al.Fast algorithms for large-scale periodic structures using subentire domain basis functions［J］.IEEE Trans Antennas Propag，2005，53(3):1154-1162.

［10］Sun B，Ping L L，He X X.Acceleration of time-domain finite-element method in electromagnetic analysis with OpenMP［C］//2010 International Conference on Microwave and Millimeter Wave Technology.［s.n.］，2010:845-848.

［11］Liu Z W，Ping L L，Sun B，et al.Scattering of 3-D objects with a new total-and scattered-field decomposition technique for FEM［C］//2010 Asia-Pacific Symposium on Electromagnetic Compatibility.［s.n.］，2010:1462-1465.