基于RSSI线性回归分析的无线传感器网络定位方法*
2014-04-24温家旺王敬东施乔明王佳伟
温家旺,王敬东,施乔明,王佳伟
(南京航空航天大学自动化学院,江苏 南京 210016)
无线传感器网络不仅仅提供监控和应用功能,更多地应用于无线传感器网络节点的定位服务,比如人员的实时监控、室内人员的移动、矿井下人员和设备的定位等。定位的基本要求有:锚节点的布置策略简单、手动配置快捷以及自校准过程。在各种定位算法中,基于RSSI测距作为一种低功率、廉价的技术得到了广泛应用。该算法常用的有两种方法[1]。
第1种方法是利用RSSI值与节点间的距离关系,需要设定环境参数,而在不同环境下参数有很大的不同。在文献[2]中,通过环境监测的实验研究表明,经过很长一段实验时间之后,环境状态产生了很大的变化,而这些变化对无线信号传输通道的特性产生了巨大的影响,传输模型的参数也随之改变,由于参数发生改变,那么利用该模型计算节点间的距离同RSSI值之间的关系将产生不可忽略的误差。文献[3]描述了一种基于RSSI测距的新方法,该文献通过测量三个以上的锚节点传递RSSI值,利用传输模型估算出环境的参数;文献[4]分析了线性回归工具测距的可行性,然而该文献使用了类似MoteTrack[5]实验,需要在实际环境中提前获取大量的实际数据确定回归模型。
第2种方法是通过实验获取“指纹”信息:通过已知位置的发射节点和接收节点测量出大量的RSSI数据,保存在RSSI与节点坐标的数据库中,位置信息可以通过获取到的RSSI值与数据库进行匹配,MoteT-rack[5]是一个典型的“指纹”定位实验。然而该方法在定位实验之前常常需要花费数天的时间进行训练,在这段时间里,测量出大量的RSSI值与位置坐标的数据。最后定位阶段,将未知节点获取的RSSI值与数据库的RSSI值进行对比,得到最匹配的位置估计值。当随着时间的推移和环境特征的变化,已知数据库将会失效,从而需要重新获取完整的“指纹”信息。
针对以上两种方法的优缺点,本文提出了一种基于RSSI线性回归分析的定位新方法。该方法利用信号衰减模型和线性回归理论结合,得到实际环境下每个锚节点的测距模型,同时加入了相关系数和剩余标准差对测距模型进行评估。最后定位过程中利用定位策略挑选出“合适的锚节点”进行定位。
1 RSSI值测距模型的修正
1.1 RSSI值测距模型存在的问题
在空间传播的过程中,随着距离的增加,信号的强度大小也随之改变,根据这个变化的值得出信号强度的衰减与空间距离的关系。普遍采用的理论模型为Shadowing模型,其具有对数衰减特性,当发射信号强度为0dBm时,其RSSI测距模型如式(1)所示:

式中:d为锚节点与未知节点的距离;n为路径损耗指数;εσ是以dB为单位,服从均值为零、标准偏差为σ的正态分布随机变量;RSSId为相距d的节点接收强度值;RSSId0为相距d0处的节点接收强度值,通常d0设定为1m。由此可以得到所测的距离d为

在测距实验之前,需要知道环境参数RSSId0和n的值。然而由于信号在不同的环境下传输的特性并非完全一致。根据文献[6-7]表明,影响Shadowing模型参数不固定的因素除了阴影效应和多径效应这两个外界原因以外,节点自身的变化也会有很大影响,尤其是天线的角度、工作电压值、节点摆放的角度等因素,也就是说,不同节点自身的因素对信号传输也会产生不同影响。
1.2 RSSI测距模型的修正
为了降低测距的误差,需要找到一种快速简便的方法对模型中的RSSId0和n两个参数进行修正。本文提出了一种利用锚节点之间的距离与RSSI值关系来修正测距模型的方法,通过信号衰减模型与线性回归分析理论的结合,然后利用最小二乘法估算出较为准确的传播因子RSSI0和n。
根据文献[2-4]可知,计算未知节点到每个锚节点的距离都使用同一参数下的模型,虽然一部分测距值的误差可能比较小,但是另一部分测距值的误差依然很大,这样会造成较大的定位误差。因此在定位过程中,通过不同锚节点获得的RSSI值转换为距离的模型可能是不同的,需要获得不同锚节点到未知节点的测距修正模型。在无线传感器网络中,具有一定数量的锚节点作为已知位置坐标的节点,它们之间的距离是已知的。利用每个锚节点之间的通信,按照设定的规则获取相应的RSSI值,将信号衰减模型与线性回归理论结合,求得每个锚节点作为发射节点时的测距修正模型。
首先设定锚节点之间RSSI值获取的规则,假设无线传感器网络中有(N+1)个锚节点。如图1所示,锚为节点0为发射节点,剩余锚节点为接收节点接收RSSI值的情形,获取到N个距离下相应的RSSI值,然后根据测距修正模型计算出锚节点0的传播因子。类似锚节点0传播因子的获取方式,剩余锚节点依次作为发射节点,接收节点获取相应距离下的RSSI值,计算出剩余锚节点的传播因子。

图1 当锚节点0作为发射节点时的信号传输图
为了获得准确的测距修正模型,对式(1)的信号衰减模型进行数学替换,假设 y=RSSI,β0=RSSI0,β= -10n,x=,可变为

其中,ε为测量的随机误差,从式(3)可以看出,RSSI与距离关系转变为RSSI与距离对数的关系,而且二者呈线性关系,因此只需知道β和β0两个未知量,就可以通过实验获取RSSI值转换为距离的对数,进一步转换为距离值。假设在实验中得到N组不同的x值(距离对数)下的y值(RSSI值),利用最小二乘估计法估计β和β0两个参数:

该测距修正模型实现的具体过程为:
第1步,(N+1)个锚节点之间相互发送和接收数据包。每个锚节点依次作为发射节点,当某个锚节点作为发射节点时,循环发送m个数据到其他N个锚节点中,这N个锚节点作为接收节点;
第2步,在以上条件下,每个锚节点都可以获取m*N组最原始的RSSI值与距离对数(在对数坐标下)的关系,将其绘制到对数坐标图中;
第3步,根据式(4)就可以计算出(N+1)个锚节点作为发射节点时的β和β0值,代入式(3)得到不同的线性回归测距方程。
1.3 修正模型的评估
受多径效应、阴影效应以及节点自身对信号传播的影响,实际的距离对数与RSSI值关系之间并不完全符合测距模型的线性关系。测距模型计算出来之后,需分析其是否适合进行测距,并计算回归精度。在回归理论中,得到回归方程之后,首先对回归方程进行显著性检验,它可以定量地说明两个变量的线性密切程度,判断出RSSI值的差异主要是由随机误差干扰引起的,还是由于距离本身的差异引起的。在回归效果显著的情况下,才能用回归直线来近似地表示这两个变量之间的关系。最后利用剩余标准差来计算回归直线的精度,剩余标准差能够反映除了距离对RSSI值影响外,其他因素对RSSI值的影响程度。剩余标准差越小,测距模型的精度就越高。
通常的显著性检验方法有三种:R检验、t检验、F检验。在一元线性回归的显著性检验中,三种检验方法虽然形式上不同,但对同一问题,在同一检验水平下,其检验效果是一致的。本文选用R检验,即相关系数检验。线性相关系数r作为相关系数的一种,常用以描述两个变量间线性相关强弱的程度。其计算公式如式(5):

式(5)中,若r为正数,说明回归方程为正相关,若为负,则为负相关。
为了简便起见,引入RSQ(r的绝对值平方根)值来表示。当RSQ值靠近“0”时,说明两个变量相关性很弱,靠近“1”时,说明两个变量相关性很强。根据相关系数r显著性表,计算出回归效果达到显著性的RSQ最小值。表1为不同自由度n-2(n为实验点)和显著性水平α为0.20、0.10及0.05时的RSQ所能达到显著性的最小值。
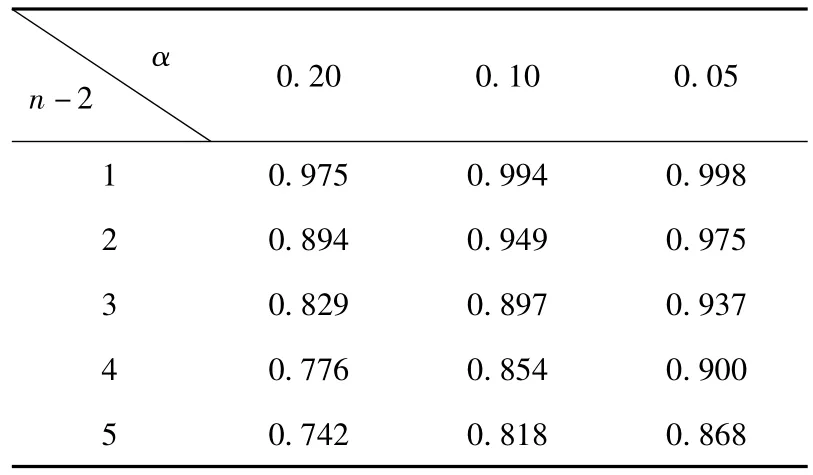
表1 相关系数显著性检验的RSQ 最小值
通过对表1的数据分析可以看出:锚节点的个数以及可信赖程度不同的情况下,测距模型达到回归效果显著的RSQ最小值也不相同。例如:n-2=2,测距模型的可信赖程度为80%时,RSQ≥0.894的测距模型回归效果才显著。而在大规模的无线传感器网络中,锚节点之间能够相互通信的个数较多,经过综合分析,将RSQ≥0.9定为测距模型回归效果较好的范围值。
在定位系统中,检验出测距模型能够适用于RSSI值测距之后,还需要计算该模型的精度水平。因为相关性越强并不完全代表测距精度越高,而剩余标准差作为回归直线精度水平的指标,在模型的回归效果显著的基础上,剩余标准差越小,反映的测距模型精度就越高。通过比较所有锚节点的测距模型,可以判断出每个锚节点的测距误差程度。对于测距精度较小的模型,需要对其剔除,否则会影响定位精度,具体剔除策略在下文将详细描述。其计算公式如式(6)所示:

式中,y和分别为测量值和回归值。
因此,式(4)计算出传播因子之后,则可以对测距模型进行评估,其具体评估过程为:
第1步,根据式(5)和式(6)计算RSQ值、剩余标准差s以及所有剩余标准差的平均值;
第2步,根据一定的定位策略,挑选出合适的锚节点,将它们加入到未知节点的定位中。
2 定位策略
在无线传感网络定位中,一跳范围以内,能够与未知节点建立通信的锚节点数目并不是固定的,有些未知节点只能与较少的锚节点通信,而有些未知节点却能够与较多的锚节点通信。在这些未知节点到锚节点的测距值中,并非所有的测距值都较准确,如果将测距误差较大的测距值加入到定位中,则可能会造成更大定位的误差。因此需要根据本文得到的测距修正模型及其评估标准,制定相应的定位策略,挑选出测距值较好的锚节点,降低定位误差。
定位策略的基本思想为:RSQ和剩余标准差s满足条件的同时挑选出的锚节点个数至少3个。将用于定位的锚节点分为三种类型:将RSQ≥0.9且s<的锚节点定为i类锚节点;将除了i类以外的RSQ≥0.85且s<的锚节点定为ii类锚节点;除了i类和ii类以外,将其他的RSQ值降序排列,把它们定为iii类锚节点,RSQ值越高,相应的锚节点用于定位的优先权越大。
具体的定位策略可分以下3种情况:
1)(N+1)<3,即一跳范围内小于3个锚节点,无法实现测距定位;
2)(N+1)=3,即一跳范围内有3个锚节点,在这种情况下,不管RSQ值和剩余标准差为多少,都不需要对锚节点进行剔除,因为如果进行剔除了个别RSQ值较小的锚节点,则锚节点个数将小于3,无法实现定位;
3)(N+1)≥4,即一跳范围内大于或等于4个锚节点,在这种条件下,分3种情况:
①i类锚节点个数大于或者等于3,将i类锚节点用于定位;
②i类锚节点个数小于3,挑选出ii类锚节点,i和ii类锚节点总数大于或者等于3,将i和ii类锚节点用于定位;
③i和ii类锚节点总数小于3,在满足总锚节点数为3个的同时,挑选出RSQ值高的iii类锚节点,然后将这三类锚节点用于定位。
具体的定位策略流程图如图2所示。根据该定位策略得到了一组用于定位的锚节点,本文称之为“合适锚节点”。修正模型的建立以及“合适锚节点”的确定这两个阶段称为锚节点的校准阶段。锚节点校准阶段可以在整个定位系统开机之后进行以及每隔一定周期进行。

图2 定位策略
3 定位实验
3.1 实验环境和锚节点布置
本文选用的无线传感器网络实验平台为基于Zigbee的CC2530硬件平台,图3为实验室环境内锚节点布置图。
其中室内环境的大小为8m*12m,每个小格为1m*1m的瓷砖地板,粉色区域为桌子以及电脑等常用的设备,白色区域为自由区域,整个实验室外围由墙壁、窗户和门组成,11个锚节点依次从序号0到10排列,锚节点的实际坐标如图所示。整个定位系统由以下几个部分组成:

图3 实验室的环境内锚节点布置图
1)网关节点(1个):通过串口与上位机进行数据传输;
2)锚节点(11个):锚节点通信距离一般大于未知节点,通过修改寄存器TXCTRLL的值,改变发射功率,确定通信半径大约为30m;
3)未知节点(1个):为了验证定位策略的性能,当未知节点处于区域的不同位置时,尽可能使得一跳范围内的锚节点数目不同,即通信半径小于10m才能满足条件。通过修改寄存器TXCTRLL,发射功率设置为最小,经过大量的丢包测试,确定通信半径大约为6m可以做到基本不丢包,最终将6m最为未知节点的通信半径;
4)电脑(1台):Microsoft Visual Studio 2005开发界面,用于数据采集和定位显示。
3.2 测距模型的获取以及“合适锚节点”的确定
根据本文的方法,未知节点定位之前,需要进行锚节点校准阶段。该阶段的第一步是所有锚节点测距修正模型的获取;第二步根据RSQ值和剩余标准差s确定“合适锚节点”。由上文的测距修正模型实现的具体过程,对以上实验环境下的11个锚节点进行测距模型的获取,然后经过计算得到相关数据,最终将这些锚节点分为i、ii和iii三种类型。具体数据见表2所示。
表中的平均测距误差分别由传统的经验模型和本文的修正模型计算得到,使用修正模型的测距误差都要小于经验模型,其中锚节点0、2、8、10下降达到50%以上,同时这四个锚节点的RSQ值都大于0.9,剩余标准差和平均测距误差也是所有锚节点中最小的四个,符合定位策略中的情况,将此4个锚节点确定为i类优质锚节点。不过由于未知节点的通信半径只有6m,定位过程中有可能不能完全接收到这4个锚节点的信号,当未知节点只能接收到一个或者两个锚节点信号时,需要增加符合条件的锚节点4和6作为ii类中等锚节点。根据这i类和ii类锚节点在区域中的分布,不管未知节点在任何位置,都至少有3个以上的“合适锚节点”能接收到未知节点的信号,因此就不需要选择第iii类替补锚节点用于定位。

表2 锚节点校准阶段的各项数据
结合图3锚节点的布置图以及表2锚节点的分类可以看出:各项参数最差的锚节点3、7和9位于横向区域中间,这三个锚节点周围存在桌子、窗户和墙壁等障碍物,信号传输路径比其他节点复杂;锚节点1和5靠近墙壁的同时,也贴近桌子和电脑等设备,造成RSQ值、剩余标准差和平均测距误差也低于平均水平;ii类锚节点4和6的位置虽然跟i类锚节点0和2对称,但锚节点4和6周围存在空调和门,也影响信号的衰减质量,不过这两个锚节点周围受到的干扰低于锚节点1和5;i类锚节点0和2虽然对称,但是它们的β0和β相差较大,由此可知,这两个节点自身也会对信号传输产生较大的影响,造成这种差异的原因可能是天线的角度、工作电压值或者节点摆放的角度等因素。
因此在锚节点布置过程中,通信半径满足要求的情况下,锚节点尽量布置于区域的边缘以及障碍物等干扰较小的地方,而且尽量将每个锚节点的自身条件保持一致。
3.3 未知节点定位
当该区域内的未知节点需要位置信息时,未知节点通过发送请求信号给周围的锚节点,锚节点接收到信号之后,获取RSSI值,最后实现RSSI值定位。本文实验过程中,将未知节点依次放置于锚节点的0~10号位置,然后使用传统的测距方法和本文的方法对未知节点进行定位。
根据未知节点的通信半径、“合适锚节点”的分布以及实验统计,未知节点在0~10号位置时,一跳范围内的锚节点个数以及相应的i类和ii类锚节点总数如图4所示。
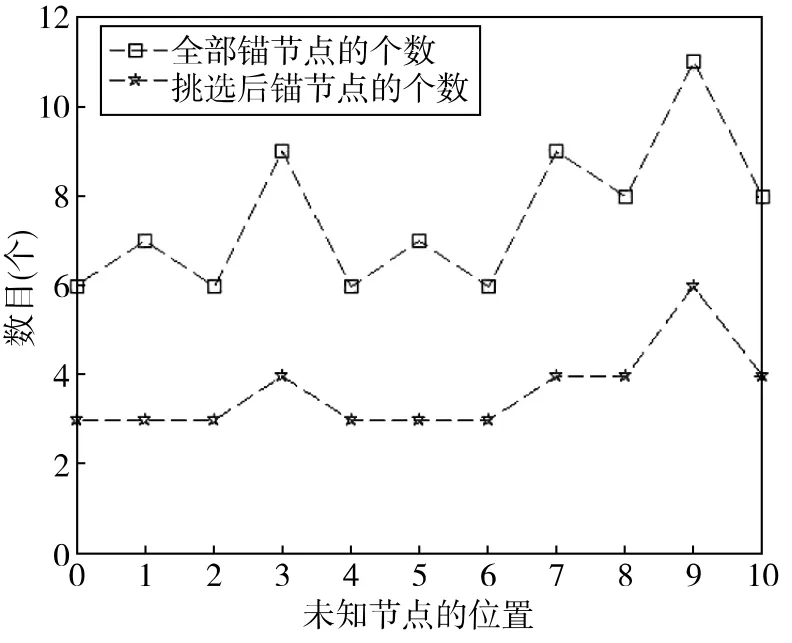
图4 一跳范围内全部锚节点和用于定位的锚节点个数对比图
从图4可以看出,加入了定位策略之后,用于定位的锚节点个数减少了50%左右。图5为利用本文的测距修正模型的情况下,未知节点在11个不同位置时的定位误差对比图。
从图中可以看出,定位策略加入之后,虽然用于定位的锚节点个数大幅度下降,但是平均定位误差却从1.41m下降到0.81m。与此同时,由图4可知,一跳范围内的锚节点个数和“合适锚节点”中的个数都不同,当加入定位策略后,未知节点在11个位置的定位误差相对于无定位策略会有所不同,并且都降低了定位误差,尤其是位置0、5、6、8和10,降低了50%左右。不过当一跳范围内的锚节点与“合适锚节点”中的锚节点相同时,定位误差不会发生变化。
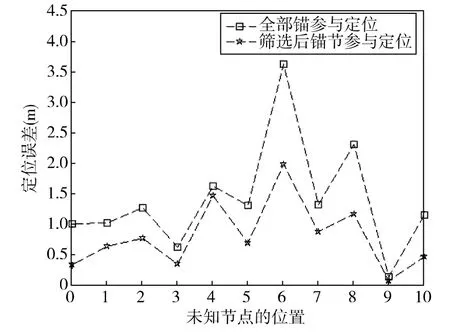
图5 无定位策略和有定位策略的定位误差对比图
图6为未知节点在11个不同的位置时,使用本文方法(测距修正模型和定位策略结合)和传统方法(经验模型)的定位误差对比图。

图6 本文方法和传统方法的定位误差对比图
从图6可以看出,使用本文的方法,有10个位置的定位误差都有不同程度的下降,尤其是位置0、2、6、7和10,下降了70%以上;虽然可能由于经验模型在位置8处RSSI值转换为距离更准确,使得该位置使用传统方法的定位误差稍微小于本文方法,但是使用传统方法的平均定位误差为1.75m,而本文方法的平均定位误差为0.81m。
除此以外,在本文的实验中,节点的发射功率为0dbm,每对锚节点之间连续发送100个数据包,每个数据包间隔20ms。当锚节点个数为5时,锚节点校准过程的时间最多需要40s;当锚节点个数为11时,锚节点校准过程的时间最多需要220s。如果加入合适的数据路由算法,还可以减少锚节点校准阶段的时间。因此相对于RSSI“指纹”识别算法需要数天的训练时间来说,本文的锚节点校准过程方便快捷。
以上实验数据和结果说明,在不增加任何设备的情况下,利用修正模型和定位策略结合方法可以较大地提升定位精度。因此,利用本文的方法,在现有的无线节点资源中,能够获得较高的定位精度和稳定性。
4 结束语
本文中提出了一种存在严重多径衰减的环境下的定位新方法。实验表明,使用RSSI线性回归分析的定位新方法,在锚节点校准阶段可以获取每个锚节点的测距模型,同时选择了用于定位的“合适锚节点”,定位精度有了明显的提升。整个定位过程避免了时间的消耗和复杂的数据“指纹”存储。因此,在未来能够在室内环境内进行实时动态无线定位。
[1]P Barsocchi,S Lenzi,S Chessa,G Giunta.A Novel Approach to Indoor RSSI Localization by Automatic Calibration of the Wireless Propagation Model[C].In Proceedingsofthe IEEE VehicularTechnology Conference(VTC),Barcelona,Spain(April 2009).
[2]K.Kaemarungsi,P.Krishnarmurthy.Properties of Indoor Received Signal Strength for WLAN Location Fingerprinting[C].In Proc.IEEE First Annual International Conference on Mobile and Ubiquitous Systems:Net working and Services(MOBIQUITOUS 04),Boston,MA,Aug,2004:14-23.
[3]P Barsocchi,S Lenzi,S Chessa,G Giunta.A Novel Approach to Indoor RSSI Localization by Automatic Calibration of the Wireless Propagation Model[C].In Proceedingsofthe IEEE VehicularTechnology Conference(VTC),Barcelona,Spain(April 2009).
[4]M Saxena,P Gupta,BN Jain.Experimental Analysis of RSSI-based Location Estimation in Wireless Sensor Networks[C].In Proceedings of the 3rd International Conference on Communication Systems Software and Middleware and Workshops(COMSWARE),Bangalore,India(5-10 January 2008):503-510.
[5]K Lorincz,M Welsh.MoteTrack:a Robust,Decentralized approach to RF-based Location Tracking[C].In Proceedings of the International Workshop on Location and Context-Awareness(LoCA 2005),Pervasive 2005(May 2005).
[6]陈红阳.基于测距技术的无线传感器网络定位技术研究[D].西安:西安交通大学,2006.
[7]Bernard F.Rolfe,Samitha W.Ekanayake.Pubudu N.Pathirana and Marimuththu Palaniswami:Localization with Orientation Using RSSI Measurements-RF map Based Approach,Intelligent Sensors,Sensor Networks and Information,2007[C].ISSNIP 2007.3rd International Conference on.Dec,2007:311-316.
