多样化军事任务舆情演化及引导的仿真

顾 健，周 莉，杨朝晖，邹 雨

(海军装备研究院，北京 100036)

随着新军事变革的发展和我海军使命任务的拓展，应对多种安全威胁、完成多样化军事任务，已经成为我海军有效履行新使命的基本模式。目前，海军遂行海上维权、海外护航、国际救援以及联合军演等多样化军事任务日趋频繁，海上活动区域大幅拓展，国际社会对我海军日益关注，导致所面临的社会舆论环境更趋复杂。而随着互联网的飞速发展，以及网络传播所具有的范围全球化、速度即时化、身份隐匿化等特点，其已成为网民自由发表看法、评头论足的自由场所。在网民有关海军多样化军事任务的评论中，虽然正面的评论不断增多，但也有一些负面内容，反映出网民对新世纪新阶段我海军使命任务的认识存在偏差和偏见，对我海军遂行多样化军事任务的实践存在误读和误解。一些别有用心的人更是歪曲传播、恶意炒作我海军遂行的军事行动，使之迅速升温为舆论热点话题，杜撰、炒作“中国威胁论”。因此，深入研究舆情演化规律并引导遂行多样化军事任务过程中所引发的舆论，具有重要的现实意义。

1 研究现状

舆情的概念有狭义和广义之分。狭义上，舆情指在一定社会空间内，围绕中介性社会事项的发生、发展和变化，作为舆情主体的民众对国家管理者产生和持有的社会政治态度［1］;广义上，舆情是指民众的全部生活状况、社会环境和民众的主观意愿，也就是通常所说的社情民意［2］。

舆情演化研究，重点是要回答两个问题:一是观点演化过程如何导致舆论的形成，即个体间如何进行观点交互;二是交互过程中各因素如何影响舆情演化的进程。国内外研究学者采用不同方法对舆情演化进行了大量研究。

国外比较典型的舆论演化模型有Sznajd模型［3］、Deffuant模型［4］和 Hegselmann-Krause 模型［5］等。Sznajd模型认为当两个相邻个体持有相同观点时，在观点距离范围内，可以说服所有其他相邻个体。Sznajd模型中的个体观点只在－1和+1中取值，而Deffuant等认为，在多数情况下，观点连续取值能够更好地对个体态度进行描述，并提出Deffuant模型。在Deffuant模型中，任一时间步长内，每一个体随机选择另一个体，当个体间的意见距离小于某一阈值时，则进行意见交互。通常，在形成观点的过程中，个体会在一定程度上参考其他个体的观点，且个体间不同的意见距离会产生不同程度的影响，基于这种思想，Hegselmann和Krause提出了HK模型，即有界信任模型。

在国内，吴青峰［6］、肖海林［7］等利用元胞自动机对舆论的演进过程进行研究。刘常昱等［8］引入个体意见的不确定性以及个体间的信任因子，建立了个体间的不对称影响函数。张立等［9］建立了具有可自行改变观点交互策略的舆论演进模型，并对参与舆论演进个体的记忆进行了建模。

舆情由许多个体意见交互作用形成，其发展变化受社会、文化、政治等多种不确定、复杂、非线性因素的影响，且涉及人的心理感受，其演化过程具有高度的复杂性、不确定性和自组织性等复杂系统的特性［10］。因此，本文基于复杂适应系统(CAS:Complex Adaptive System)理论，采用Agent建模方法建立舆情演化模型。

2 演化模型构建

Agent建模方法从复杂系统的个体行为层面建立模型，其基本思想是根据复杂系统特点提取个体属性，并分析个体之间的关系及相互作用，建立个体间的交互模型。因此，基于Agent建模方法构建演化模型的关键是个体Agent属性的描述及个体Agent间交互模式的建立。

舆情演化的本质是个体间观点的交互作用，个体观点(或个体意见、态度、情感倾向等)是舆情演化模型的基础。因此，个体Agent的属性用个体所持观点表示。

当前，个体观点主要有两种表现形式:离散表示和连续表示。离散表示，采用－1(反对)、0(中立)、1(支持)或其它离散数值表示个体观点，观点之间截然分开，互不相交。连续表示，一般采用连续区间［0，1］表示个体观点。

现实社会中，绝大部分个体的观点并不总是明确无误的，尤其在形成稳定舆情前，很多个体的观点是模糊、摇摆的，观点的连续表示更具实际意义。因此，参考文献［8］的表现形式，将个体Agent的观点属性表示为:A(o，u)。

其中，o(opinion)表示个体观点，取值范围为o∈［0，1］，取值为0时表示高度反对，取值为1表示高度支持，其它数值表示种种中间观点;u(uncertainty)表示个体对自身所持观点的不确定程度，取值范围为u∈［0，0.5］，取值为0时表示对自身所持观点极度确定，一般不会改变，取值0.5时表示对自身所持观点很不确定，很可能受其它个体影响而改变。当u的取值较小时，一般称其对应的个体为“极端个体”，这些个体的态度较为坚定，对自身观点更加确定，不易受他人影响改变自身态度。

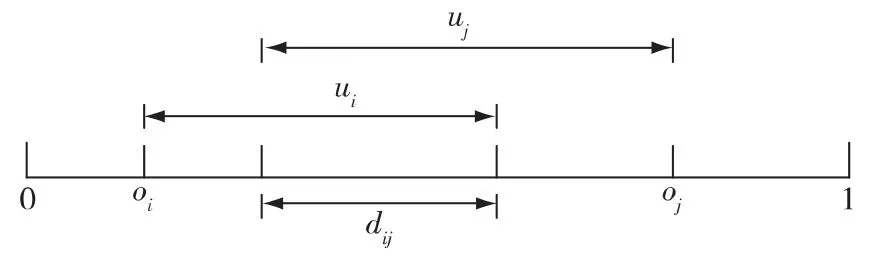
图1 dij计算示意图

如图1，定义个体i:Ai(oi，ui)和个体j:Aj(oj，uj)之间观点交互区间的大小如下:

个体i与个体j交互时，各自对对方的影响因子定义如下:

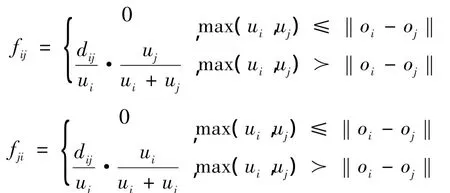
其中，fij表示个体i对个体j的影响因子，fji表示个体j对个体i的影响因子。个体间交互后各自的观点属性计算如下:

如上定义的交互准则，比较准确地反映了现实社会实际舆情演进过程中，人们进行观点交互行为如下:

1)当个体间的意见距离足够大时，他们之间不会对彼此产生影响;

2)个体间的相互影响程度，受个体间观点交互区间大小的影响，交互区间越大则彼此间的影响越大;

3)个体间的相互影响具有不对称性，观点不确定程度小的个体(即对自身观点更加确信的个体)对不确定程度大的个体的影响，比对方对自身的影响要大。即自信的个体更容易影响不自信的个体。

3 仿真实验

3.1 实验设置

对舆情演化过程进行仿真，除了舆情演化模型的建立，还需考虑舆论的传播网络。在舆论传播过程中，个体通过特定话题的引用关系形成一个传播网络。研究表明［11］，舆论的传播网络具有无标度特性，因此，在仿真实验中采用无标度网络作为舆论的传播网络。

当前，主要的Agent建模仿真平台有:Swarm、NetL-ogo、Repast和Ascape等，本文采用NetLogo仿真平台。NetLogo仿真界面如图2所示，包括参数设置、建模环境和结果输出三部分。参数设置部分用于设置仿真实验的初始参数;建模环境能够显示个体交互及观点变化的动态过程;结果输出部分通过变量及图形等形式，输出仿真结果。

图2 单一中立舆情的涌现

为了便于实验结果的显示，将观点区间［0，1］均匀划分为五部分，分别表示五类观点:“强烈反对”、“反对”、“中立”、“支持”和“强烈支持”。为描述观点的收敛程度，参考文献［10］定义舆论熵如下:

其中，p1～p5分别表示五类观点的个体数占总个体数的比重。舆论熵越小，意味着观点越统一。图2中四幅输出图形分别表示舆论熵、五类观点个体数的动态变化、五类观点个体数占总个体数的比重以及具有不同观点不确定性值的个体所占比重。

3.2 舆情演化实验

为考察参数对舆情演化的影响，在多个参数集下，对所建模型进行仿真实验。现实社会中，舆情演化具有多种多样的初始状态，本文对几种典型的情形进行仿真:初始观点均匀分布、某类观点占据多数以及极端个体的影响。

1)初始观点均匀分布

实验时，设置个体总数为300，假设所有个体观点在［0，1］区间均匀分布，为了便于分析，假设所有个体的观点不确定性值相同。如图2，在u=0.5的初始状态下，随着个体交互的进行，最终涌现出单一中立舆论。

如图3，逐渐减小观点不确定性值，实验结果显示，u越小涌现出单一中立舆论的时间越长，且其他观点区间的个体也越多。如图3(c)，当u小于某一数值后，最终不会涌现出单一舆论。

实验表明，在初始观点均匀分布的初始条件下，当u较大，即个体的从众性较强时，会涌现出单一中立舆论;而u越小，即个体越自信，越难形成单一舆论，最后的个体观点越分散。上述结论与现实情况是相符合的。

图3 初始观点均匀分布的仿真输出结果

2)某类观点占据多数

“沉默的螺旋”理论认为，个体观点的表明是一个社会心理过程，当个体发现自己属于“多数”或“优势”观点时，他们便倾向于大胆表达自己的观点;当发现自己属于“少数”或“劣势”观点时，便可能会屈服于环境压力而转向“沉默”或“附和”。下面对这一情形进行仿真，所有仿真实验均重复10次，结果取其平均值。

实验时，设置个体总数为300，假设所有个体的观点不确定性值u=0.5，当初始观点在［0，0.4］区间(观点为强烈反对和反对)的个体分别占总数的50%、54%、58%、62%和66%时，舆情演化稳定后，观点在［0，0.4］区间的个体占总数的比例分别为3%、68%、92%、93%和93%。可见仿真结论与“沉默的螺旋”理论相符合。

逐渐减小观点不确定性值，仿真结果如图4所示。可以看到当个体观点的初始分布不同时，u值变化所产生的影响也不同。

当初始分布位于［0，0.4］区间的个体比例为50%时，u越小，舆情演化稳定后，观点位于［0，0.4］区间的个体越多。其原因在于，初始个体比例为50%时，还不足以占据统治优势形成单一“反对”舆情，当u较大、个体的从众性较强时，最终往往会涌现出单一中立舆论，导致位于［0，0.4］区间的个体很少，但随着u减小，个体越来越自信，越难以形成单一中立舆论，导致位于［0，0.4］区间的个体逐渐增加。

图4 不同u值及观点分布条件下的仿真结果

当初始分布位于［0，0.4］区间的个体比例大于54%时，u越小，舆情演化稳定后，观点位于［0，0.4］区间的个体越少。其原因在于，［0，0.4］区间的初始个体比例大于54%时，其占据了统治优势形成“反对”舆情，导致位于［0，0.4］区间的个体较多，但随着u减小，个体越来越自信，［0，0.4］区间这种由于初始数量多而具有的统治优势逐渐弱化，导致位于［0，0.4］区间的个体逐渐减少。

因此，上述仿真结果与现实情况在直观上也是吻合的。

3)极端个体的影响

图5 极端个体的影响

以上实验均假设所有个体的观点不确定性相同，现实社会中，不同个体对自身观点的不确定性可能是不同的，因此，本节考虑极端个体(u较小)对舆情演化的影响。

实验时，设置个体总数为 300，［0，0.2］和［0.8，1］两个区间均为极端个体，各占总数的10%，观点不确定性值u=0.1，其它区间个体均匀分布，不确定性值u=0.5。仿真结果如图5(a)所示，最终涌现出二元舆论，且经过交互，个体观点的不确定性值整体趋于变小，即整体对自身观点趋于更加自信。

在上述基础上，将［0.4，0.6］区间的个体设置为极端个体，同样占总数的10%，则如图5(b)所示，最终涌现出三元舆论。

3.3 舆情引导实验

本节仿真在舆论环境中加入一些支持己方观点的极端个体进行舆情引导的情形，对初始条件下有、无极端个体的引导情况分别进行了仿真实验。

1)无极端个体

实验时，设置个体总数为300，持反对观点的个体(观点位于［0，0.4］区间的个体)占总数的70%，其它区间均匀分布，不确定性值均为u=0.5。进过一段时间演化，观点在［0，0.4］区间的个体占总数的91%，此时，在［0.8，1］区间加入50个u=0.1的极端个体进行引导，引导后的舆情演化结果如图6(a)所示，持反对观点的个体数量几乎没有变化，引导不成功。

改变引导策略，在初始条件下进过一段时间演化，涌现出“反对”舆情后，在［0.4，0.6］“中立”观点区间加入50个u=0.1的极端个体进行引导，引导后的舆情演化结果如图6(b)所示，负面舆情很快向着“中立”方向演化，有效地引导了舆情。

将上述仿真结果与社会现实情况进行比较，社会心理学家对这一现象的研究表明:与被引导个体完全相反的舆论引导容易激发被引导个体的心理反抗情绪，类似于通常所说的逆反心理。因此，仿真结果与现实情况是相吻合的。

2)有极端个体

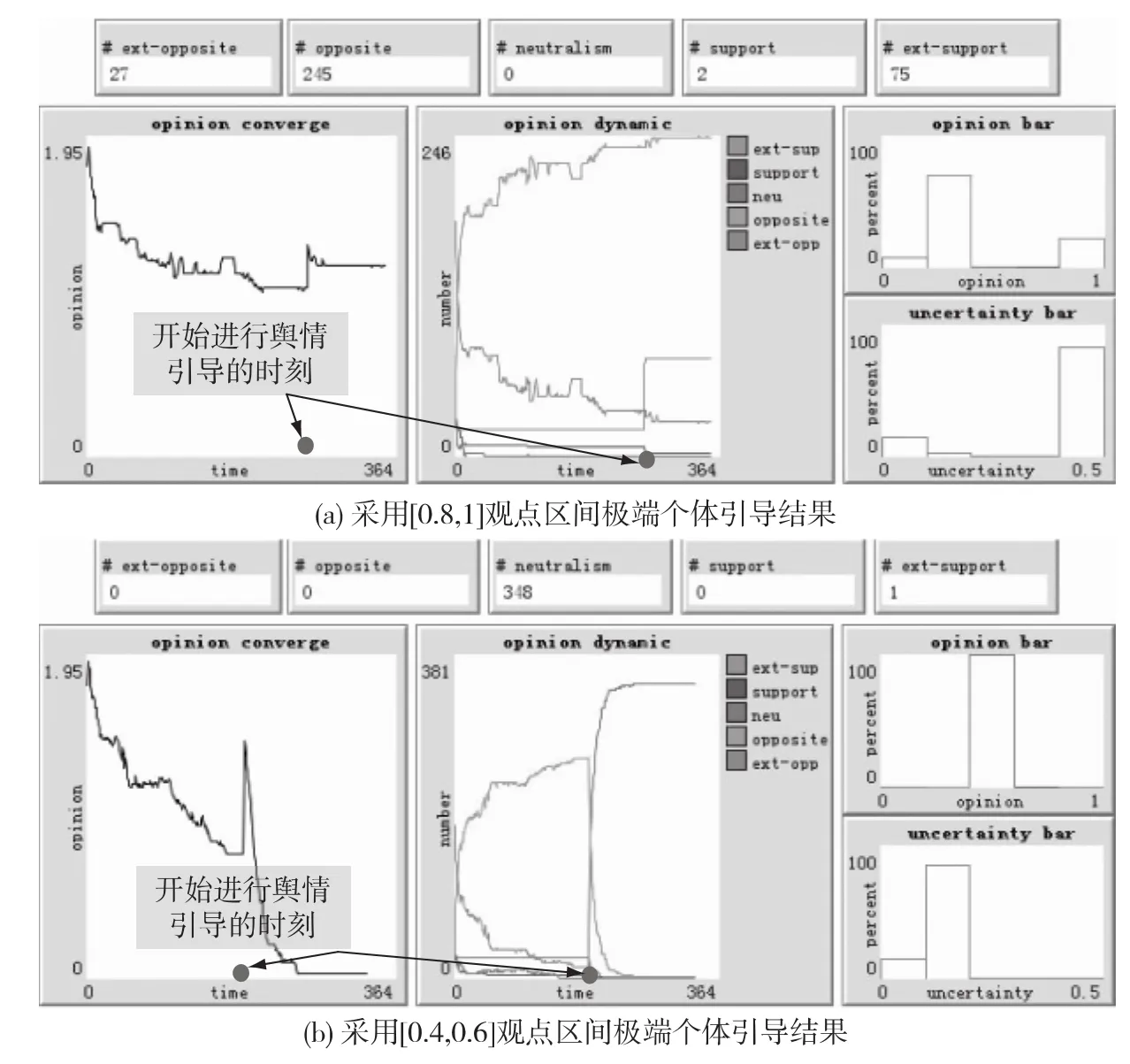
图6 无极端个体的舆情引导结果

实验时，设置个体总数为300，位于［0，0.4］区间、持反对观点的个体有210，占总数的70%，基于上节结论，采用［0.4，0.6］区间u=0.1的极端个体进行舆情引导。对反对观点中极端个体所占比重分别为10%、20%、30%、40%、50%，嵌入引导个体的数目分别为50、100、150、200 的初始条件分别进行仿真，每类初始条件均仿真10次，结果取平均值。

舆情引导后，持反对观点的个体数如图7所示。从图中可以得出如下结论:1)初始极端反对个体越多，舆情演化稳定后反对个体相应越多;2)嵌入式引导的个体越多，引导效果越好，但由于极端反对个体的意见不确定性很小，较难改变其观点，同时其还会对周围个体产生负面影响，因此，这部分人难以给予引导，必须配合采取删帖或其它强制性措施。

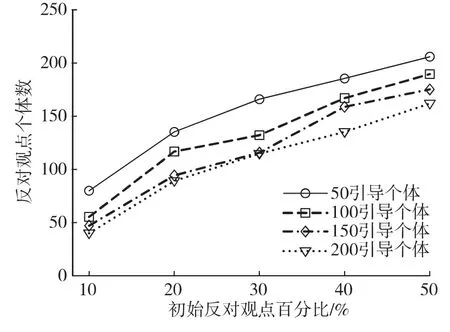
图7 有极端个体的舆情引导结果

4 结束语

本文采用基于Agent的建模理论与方法，根据现实社会实际舆情演进过程中，人们的观点交互行为，对个体间观点交互的规则进行建模，建立了舆情演化过程的模型。采用所建模型对初始观点均匀分布、“沉默的螺旋”、极端个体的影响以及不同引导措施所产生的效果等典型情况进行了仿真实验。模型仿真实验的结果，不但符合新闻传播、社会心理学等领域的“沉默的螺旋”和“逆反心理”等现象，而且与人们的直观认知也是相符的，表明所建模型符合实际社会中个体交互和舆论演化的特点。因此，可以通过模型研究影响舆情演化的关键因素，从中找出舆情演化、引导的一般规律，以更好地为我海军遂行多样化军事任务的舆情引导服务。

［1］王来华.舆情研究概论:理论、方法和现实热点［M］.天津:天津社会科学院出版社，2003.

［2］张克生.国家决策:机制与舆情［M］.天津:天津社会科学院出版社，2004.

［3］K.Sznajd，J.Sznajd.Opinion Evolution in Closed Comununity［J］.International Journal of Modern Physics C，2000，11(6):1157-1165.

［4］G.Deffuant，D.Neau，F.Amblard，G.Weisbuch.Mixing Beliefs Among Interacting Agents［J］.Advances in Complex Systems，2000(3):87-98.

［5］R.Hegselmann， U. Krause. Opinion Dynamics and Bounded Confidence Models， Analysis， and Simulation［J］.Journal of Artificial Societies and Social Simulation，2002，5(3):2-34.

［6］吴青峰，孔令江，刘慕仁.元胞自动机舆论传播模型中人员个性的影响［J］.广西师范大学学报(自然科学版)，2004，22(4):5-9.

［7］肖海林，邓敏艺，孔令江，等.元胞自动机舆论模型中人员移动对传播的影响［J］.系统工程学报，2005，20(3):225-231.

［8］刘常昱，胡晓峰，罗批，司光亚.基于不对称人际影响的舆论涌现模型研究［J］.系统仿真学报，2008，20(4):990-992.

［9］张立，刘云.舆论演进中个体策略选择的仿真研究［J］.系统仿真学报，2009，21(12):3518-3521.

［10］胡晓峰，罗批，张明智，等.社会仿真——信息化战争研究的新领域［M］.北京:电子工业出版社，2010.

［11］Barabasi A L，Albert R.Emergence of Scaling in Random Networks［J］.Science，1999，286:509-512.