基于系统理论方法的炮兵弹药消耗量预测修正方法

2014-04-24闻传花

指挥控制与仿真 2014年3期

陈俊，朱江，闻传花，周昊

(南京陆军指挥学院，江苏南京 210045)

弹药保障的“适时适地适量”必须建立在对弹药消耗量的准确预测基础上。因此，弹药保障的关键问题是需求预测问题。

通过经验数学公式进行弹药需求预测仍然是目前最主要的方法。比如文献［1］考虑到了弹药威力、毁伤幅员、目标重要性、目标易毁性、地段幅员、毁伤程度等因素，给出了基于目标任务量的弹药消耗预测公式。文献［2］中考虑到了我方实力、武器射速、作战持续时间等因素，给出了基于能力的弹药消耗预测公式。上述基于公式的弹药消耗预计方法［3］，往往只考虑影响弹药消耗的部分因素，不能全面的考虑弹药消耗问题，造成了消耗量预测精度较低。比如以XX战例为参照，根据《炮兵火力毁伤教程》的任务量方法进行计算。该方法算得消耗炮兵弹药为12.121千标弹，而实际弹药消耗量为14.065千标弹。方法误差为13.8%。加之公式不能适应发展变化，为此军事专家考虑对公式进行修正，例如针对炮兵武器射程因子计算公式不准导致直瞄武器效能偏大，进而导致弹药消耗量偏小的问题，南京陆军指挥学院赵定烽等人在通过对历史数据拟合和推导新公式基础上加以改良，但获得有价值的修正公式耗费了该研究小组半年的精力，相当困难。尤其当因素较多、相互交织，呈现复杂性和非线性的时候，公式背后的原理都不甚清晰，更谈不上对公式进行修正。

于是，引入神经网络方法进行修正能改善公式的预测精度［4］。比如在文献［5］中使用作战持续时间、地形地貌、气象气候、作战态势、射击精度、兵力损耗、目标类型、毁伤指标因子、通信指挥9个因子，构建三层的神经网络，通过对历史数据进行学习，确定修正系数，然后输入数据进行预测。针对同一战例，得到消耗炮兵弹药为13.015千标弹，方法误差为7%，在可接受的误差范围内［6］。但是神经网络方法学习所得的参数结构，能看到的只是数字连接的输入与输出，对于所反映的因素组成结构则是一个黑箱，“眉毛胡子一把抓”，无法解读其军事含义。且神经网络结构所反映的因素之间的相互关系虽被拟合，但拟合中的思维过程难以展现，当换一种环境，约束条件发生变化时，需要重新训练，同样耗时耗力。

1 研究方法

1.1 系统观视角

系统观认为:宇宙间一切事物和现象均可以构成系统，系统是由相互作用和相互依赖的若干组成部分结合的具有特定功能的有机整体［7］。基于此观点，我们将所有与弹药消耗相关的作战和保障定义为弹药消耗系统。消耗量及保障需求的大小受到了系统所有因素的影响。

系统科学最基本的观点就是承认系统的整体性，体系作战条件下，各作战要素相互依赖性增强，作战系统内部关系复杂，使得对弹药保障的影响非线性化和复杂化。现代作战的复杂性导致弹药需求影响因素错综复杂，弹药消耗预测因素之间相互影响和相互制约，公式法还原解析不可取。而采用基于系统整体的系统动力学方法(System Dynamics简称 SD)［8］，在解决问题时，不苛求数学上的严密，也不要求数据完整，在掌握系统部分机制基础上就可以建立实验模型，进行综合的研究。面对复杂的实际问题，SD能把信息反馈的控制原理与因果关系的逻辑分析结合起来进行研究。

层次观是系统科学的一个主要观点，任何复杂系统均是分层次的，层次之间既互相联系又互相区别。由于认识能力的限制，受不同层次很多因素共同影响的一个大系统，人们难以一蹴而就阐释它，而只能逐步地去认识它。虽然现有的研究成果从作战层面、武器层面、后勤保障层面分别对弹药需求的影响因素进行了探讨和分析，但还是一鳞半爪，尚未对这些数量众多、彼此交织的因素进行结构性的梳理。系统理论中，对系统结构分析的方法有解析结构模型(ISM，Interpretative Structural Modeling)［9、结构方程建模方法(SEM，Structural Equation Modeling)［10］、因果分析［11］等方法，这些方法可以分析影响因素之间的内部结构、层次及因果关系。

在系统观指导下，本文研究方法的基本思路是:从系统的角度把握弹药消耗影响因素之间的相互关系。引入常用的系统结构模型化技术ISM法进行弹药消耗结构分析，为准确确定弹药需求提供科学依据。进而利用SD仿真方法构建弹药消耗模型，对影响作用不清晰的因素运用实验探索消耗规律，形成切合作战经验的修正方法，并将专家经验所蕴含隐性知识显性化，用以指导弹药预测。

1.2 方法步骤

方法的基本步骤结合图1说明。

1)对弹药消耗进行研究，列出弹药消耗的影响因素，根据经验知识提取确定要素。

2)对于军事专家比较清晰其作用的要素关系，使用ISM分析结构，对弹药消耗系统影响因素进行分析，形成弹药消耗因素结构模型。

3)对于要素与消耗系统的关系不明确，或要素间关系不清晰，或存在动态行为，难以使用静态结构反映的情况，通过建立SD模型，进行试验探索要素的作用，研究在“IF-Then”条件下的弹药消耗量动态变化趋势。为研究要素与系统的关系、作用获取实验结果，得到分析结论，并固化为人的经验知识。

4)整个过程是一个迭代反复的过程，反映了知识形成过程。将不清晰的知识逐步清晰化，将清晰的知识结构化。

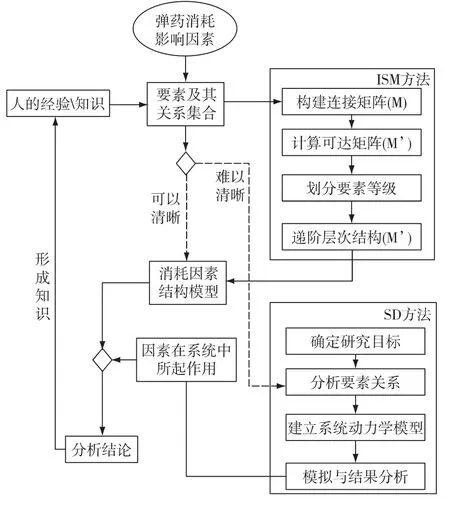
图1 方法步骤示意图

下面以研究炮兵群的弹药保障需求问题作为背景，在该方法的指导下，对弹药消耗预测量进行有针对性地修正。

2 运用ISM分析炮兵群弹药消耗因素结构

ISM分析法可使得众多元素之间的错综关系层次化、条理化，有效地分析和揭示复杂的关系结构。ISM的基本流程包括构建连接矩阵、计算可达矩阵、划分要素等级，形成递阶层次结构［12-13］。

召集专家100名，通过集中研讨，列出该弹药保障需求问题要考虑的基本影响因素如表1。

表1 影响因素

这些因素的选择根据专家的筛选，部分因素被删除，比如我综合能力是打击能力、防护能力、机动能力、侦察能力的综合体现，但在研究弹药消耗问题时，防护能力、机动能力、侦察能力都不是直接因素，为突出重点，可以暂时不加以深入考虑。

2.1 邻接矩阵构建

将要素一一比较，当两者有直接关系时，令(Si，Sj)=1，当Si和Sj无直接关系时，(Si，Sj)=0，其中(i，j=1，2，…n)，以此建立邻接矩阵，如图2所示。

图2 邻接矩阵

2.2 计算可达矩阵

根据因素的相关性，建立可达矩阵。可达矩阵是指用矩阵形式描述有向连接图各节点之间，经过一定长度的通路后可以到达的程度，通过对邻接矩阵A的运算，可求出系统要素的可达矩阵M。

其计算公式为M=(A+I)T，其计算方法为，利用布尔代数运算规则，令A1=A+I，其中I为与A同阶次的单位矩阵，其余元素为“0”，根据下式确定要素到达最大的传递次数。

计算得到的可达矩阵如图3所示。

图3 可达矩阵

2.3 划分要素等级

将可达矩阵中的要素划分为可达集、先行集和共同集。

可达集:要素Si可以到达的要素集合定义为要素Si的可达集，用R(Si)表示，由可达矩阵中第Si行中所有矩阵元素值为1的列所对应的要素组合。

先行集:可以到达要素Si的要素计划定义为要素Si的先行集，用A(Si)表示，由可达矩阵中第Si列中的所有矩阵元素值为1的行所对应的要素组成。

2.4 形成递解层次结构

一个多级递阶结构的最高级要素集(即第一层要素)是指除了可以到达自身外，不能到达其它要素的要素组成的集合。

表2 矩阵划分

其可达集R(Si)中只包含它本身的要素集，即R(Si)=R(Si)∩A(S)，例如见表2，S1该级满足条件，为最高级要素。找出最高级要素集后，即可将其从可达矩阵中划去相应的行和列，再从剩下的可达矩阵中继续寻找找新的最高级要素(即第二层要素)。依次类推出各层要素集。

第一层要素为{S1};

第二层因素为{S10};

第三层因素为{S2，S3，S11};

第四层因素为{S5，S12};

第五层因素为{S4，S6，S7，S8，S9}。

根据分层要素，建立解释结构模型，如图4所示。

图4 解释结构模型

根据图4，可以分析得出以下结论:炮兵群总的弹药需求(S1)由若干阶段弹药需求(S10)组成，阶段弹药需求(S10)的确定包括:由敌毁伤程度(S2)来确定本阶段的火力打击毁伤指标，综合能力(S3)是作为完成火力打击任务的能力，战法(S11)作为完成任务的手段方式，确定本阶段火力打击的方式、方法、时机、时间。炮兵综合能力(S3)是以火力打击能力(S5)为主，该项能力由弹药性能(S4)，毁伤概率(S8)，武器射速(S6)、命中精度(S9)，目标特性(S7)综合决定，其中弹药性能、毁伤概率、命中精度紧密相关。可见该结构分析模型比较符合我们的认知，便于我们将任务量法的一些公式隐含的知识显性化。但从模型中，应当注意到虚线圈所含S12-S11-S10此枝，战法运用(S11)的灵活性很强，因素较难划分，但有一点可以明确，敌我兵力比(S12)是重要的参考因素。孙子兵法中“十则围之，倍则分之“即是名证。但在任务量法的公式中“阶段-战法-兵力比”参数链并无体现。可初步断定任务量法存在误差的根源在于它缺乏对此“阶段-战法-兵力比”的分析缺失，尤其对兵力比影响消耗的影响没有量化，修正需要从此入手。

3 运用SD方法探索影响弹药消耗的因素

“阶段-战法-兵力比”参数链中还存在很多隐性的知识，尤其对于战法，指挥员众说纷纭，难以形成共识，对其分析会引入众多不确定因素，不能简单推理得到，难以构建ISM层次模型，更难以进行定量分析。为此构建反映战法的SD仿真作战模型，通过实验研究因素的作用及强度。基本流程包括确定目标，系统动力学建模、模拟与结果分析。

3.1 确定目标

分析战法中，炮兵对抗过程。炮兵群通常将一定数量的自行加榴炮配置在一定幅员的地域内，火炮在一个阵地上发射一定数量的弹药后，立即撤离原发射阵地，迅速机动转移到新的发射阵地再投入射击行动，如此不断变换发射阵地，直至完成规定的战术任务为止。该过程反映了自行火炮机动地域作战模式的一个基本周期，实际战斗过程无非是这个基本周期的重复。

3.2 系统动力学模型

从上述地炮对抗过程双方力量逐次投入交战，彼此激烈对抗的特点入手，描述系统有关因素，隔离划分系统的层次与子结构，分析系统整体的与局部的反馈关系、反馈环路及它们的耦合;估计系统的主导回路及其性质与动态转移的可能性通过观察反馈环的相互制约关系，在此基础上，绘制流图;建立数学方程、描述定性与半定性的变量关系;构建SD模型，如图5。

程序赋予原始数据，强调产生结果的条件，采用“If-Then”(条件—结果)的形式作为有条件的控制［14］，在计算机上模拟实验。绘制结果曲线图表，并调整数据，反复模拟实验;调整初始红蓝兵力条件，以及红蓝的损耗率，转移率观察弹药消耗结果，得到结果如表3。

表3 兵力比、损耗系数比对弹药消耗影响

3.3 结果分析

动态弹药消耗量和兵力的比值有直接的关系，在兵力1.5∶1～3∶1的时候，弹药消耗量明显增多，但是从兵力比4∶1后，弹药消耗量反而减少，此时红方压倒优势，红方兵力损失不大，所以可以逐渐忽略对抗中武器、弹药的损耗。

在兵力相同的基础上，消耗量与损耗系数有直接的关系，但是这与兵力比有区别，只要兵力一定，虽然随着损耗系数比例的增加，弹药消耗量逐渐接近基于任务法计算的弹药消耗量，但是变化的趋势没有兵力比变化得那么快，在3∶1之后，动态弹药量的需求比较平稳，减少量不大。但计算结果都比基于任务量法计算的要多。

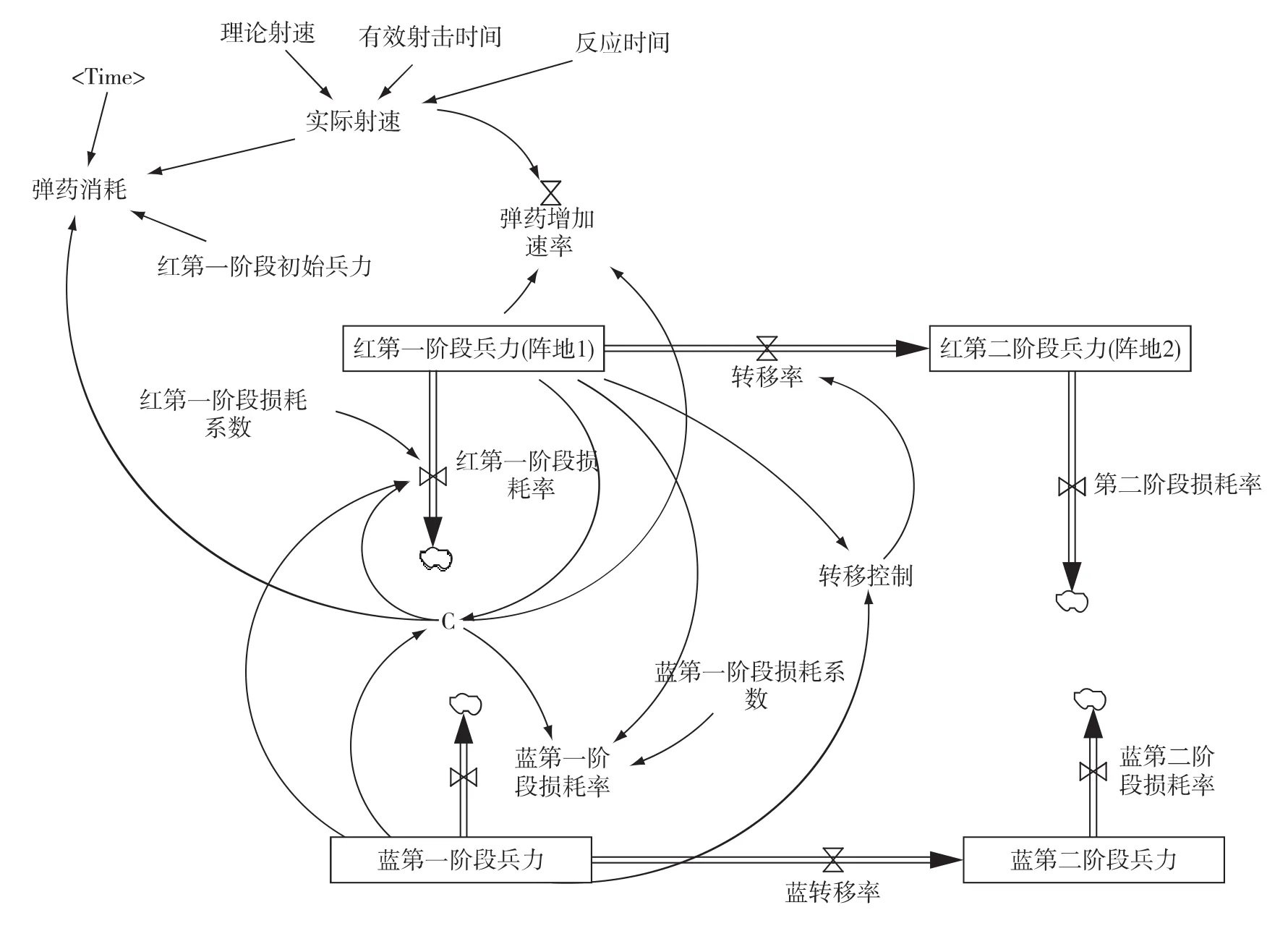
图5 炮兵对抗系统动力学流图

该结论用以修正弹药消耗预测模型，以同一战役为例，基于任务法计算的消耗量为12.121，我敌兵力比3∶1，敌我损耗系数之比4∶1，则消耗量为12.121*1.038*1.096=13.789。误差约为2%，可见大大提高了弹药消耗的精度。

4 结束语

采用公式计算时，由于公式的严格约束，一旦因素不在约束内，公式往往不能直接使用，其结果的可信度往往被人质疑。通过ISM方法建立弹药需求的影响因素解释结构模型，便于从本质上理解系统，并对需求预测问题进一步深入分析。当基于任务量的计算方法效果不够理想时，解释结构提示要考虑自身的生存和对敌的打击。那么在计算的时候就可以有针对性地进行修正。

但ISM法中要素邻接关系矩阵是直接由专家组讨论所定。人们有时会怀疑:对于未来作战，专家经验就一定能起作用?如果专家本来就很清楚，那解释结构又有什么价值?有时专家对于因素之间的关系并不是那么确认，为此，20世纪80年代末，安德森建议，在理论建立与发展过程中，通过探索性分析建立模型，再用验证性分析来验证模型。对于弹药消耗问题，使用结构方程模型探索性分析因素结构，在此基础上，采用系统动力学方法构建模型，可以进一步采集仿真数据样本，将得到的结论去分析去验证，专家可以进一步审视。

采用系统动力学方法进行预测，强调产生结果的条件，采用“If-Then”的形式作为有条件的预测。作战系统是一类受到指挥、控制、各种因素强烈控制的受控预测系统，与不受主动环节的人强烈控制的系统—自然预测系统可以采用精确分析、定量公式计算不同。受控—预测系统注重一定条件下的结果。对作战中可能受到的控制作用加以考虑，作出符合多种变化的预测。构建系统动力学模型实验可知，当考虑敌我兵力比和损耗系数比情形下的弹药消耗规律，实验获得了定量的数据，同时考虑了以前未曾考虑的损耗系数比因素。

［1］杨绪明.陆军火力毁伤教程［M］.北京:解放军出版社，2007.

［2］樊胜利，田伟峰，柏彦奇.地面主战武器常规弹药消耗预测方法研究现状［J］.2010，21(5):106-110.

［3］朱培涛，赵武奎，张华才，等.弹药消耗预测方法比较研究［J］.兵工自动化，2007，26(4):2-4.

［4］黄天辰，韩京才，叶术青，等.基于神经网络的弹药消耗预测［J］.军械工程学院学报，2004(4):29-33.

［5］刘涛，彭世袭.改进BP神经网络在航空弹药预测中的应用［J］.探测与控制学报，2009，31(5):52-56.

［6］沈寿林，朱江，等.作战复杂系统关键技术及应用［R］.国防科技报告，2007.

［7］李宏伟，熊云，李宁，王兰芳.基于系统理论的工程兵破障弹药消耗分析［J］.工程装备研究，2010，29(6).

［8］王仪山，宋莉.信息化条件下作战物资储备与消耗系统动力学仿真研究［J］.后勤指挥学院学报，2010(4):96-99.

［9］郭泳亨，龚传信，李文生.基于ISM的面向目标的弹药需求影响因素分析［J］.四川兵工学报，2010，31(4):13-15.

［10］李闯，张执国.基于SEM的航空装备战备完全性影响因素及对策分析［J］.航空维修与工程，2009(2):63-65.

［11］石峰，侯洪涛，李群，等.大规模战役仿真分析中的因果追溯方法研究［J］.系统仿真学报，2006，18(5):1110-1115.

［12］黄炜.黑客与反黑客思维研究的方法论启示——解释结构模型新探［D］.广州:华南师范大学，2003.