分布式态势感知一致性分析与度量方法研究*
2014-04-24陶九阳张东戈赵慧赟
黄 匆,陶九阳,张东戈,赵慧赟
(解放军理工大学指挥信息系统学院,江苏 南京 210007)
基于信息系统的一体化联合作战中,由指挥控制(Command and control,C2)关系网[1]连接起来的各种作战单元,地理上分散,种类上多样,性能上差异悬殊,为了有效地实现协调动作和一致性地决策,需要保证彼此有一致的态势感知。因而,一致的态势感知,是作战团队有效决策和协调行动的重要前提。对作战团队态势感知(Team Situation Awareness)[2]的一致性进行分析与度量,可以帮助我们更好地理解一致性的形成机制和影响要素,更全面地评估作战团队协同能力,更科学地设计适应协同作战需求的C2关系网络。
近年来,态势感知的一致性问题受到了广泛关注。文献[3]分析了“描述共享态势感知程度”应该考虑哪些问题,尤其在共享态势感知程度分析方面取得了一定的成果。文献[4]将个体态势感知整合到有协作的团队行为中去,认为团队成员之间相互信任的稳固性(Soundness)和完备性(Completeness)是衡量团队态势感知的主要指标。文献[5-6]提出分布式态势感知理论(Distributed Situation Awareness,简称为 DSA),从系统综合的层次,对动态系统中的分布式态势感知问题提出了一种包含行为过程的描述方法。文献[7]定性描述及构建态势感知模型体系结构框架,研究了由特定Agent组成的指挥控制网络的态势感知问题。
以往的研究虽然取得了不少成果,但大多集中于定性地描述团队态势感知一致性,而很少涉及一致性过程的定量分析,对一致性的度量大多采用主观经验和实验统计学的方法。DSA理论的提出,为研究一致性过程提供了理论基础和系统性方法,使得一致性的定量分析和客观度量成为可能。本文根据DSA理论的行为过程描述,分析了DSA一致性涌现过程,建立了一致性动力学模型和度量方法,并应用仿真计算验证了方法的有效性。
1 分布式态势感知的一致性建模
1.1 分布式态势感知的一致性涌现
DSA理论从系统综合的层次,描述了团队态势感知的动态行为过程。从系统的角度来看,尽管各作战单元的类型不同[1](传感单元,决策单元,执行单元),但都能够独立完成Endsley态势感知模型中的察觉、理解、预测三个过程[8],具有近似相同的个体行为过程,由此可以将各类作战单元设定为Agent,而作战团队可看作多个Agent相互协同的系统。系统的态势感知定义为系统中某时刻与任务相关的认知(task-related knowledge)[5],它分散于各 Agent当中,由 Agent根据环境变化实时地调整。系统态势感知的形成过程可分作两个阶段:个体认知阶段和团队协同阶段。
在个体认知阶段,各Agent根据任务分工,实时地对客观态势要素进行感知并形成个体认知。由于各A-gent观察态势的角度不同,分析态势的经验、能力有差别,即使对于相同的客观态势,也会形成不同的个体认知(individual SA)。
在团队协同阶段,各Agent通过沟通(communications)实现个体认知的共享。沟通的方式是语音或非语音信息(例如邮件,文件等)的交换[9],由互联互通的信息系统支撑。沟通的对象是所有执行相关作战任务的Agent,但沟通受到组织结构的约束。在作战行动中,执行相关作战任务的Agent,按照一定的组网原则构成C2关系网,沟通仅在网络上相邻的Agent间进行。不相邻的Agent间不直接沟通,那些需要沟通的信息(这里指个体认知)可以认为已经“蕴含”于中间节点的沟通之中,因此,可以将它看作一种经过中间节点感知的“间接沟通”。举例来说,营级指挥单元虽然不直接向师级指挥单元汇报,但汇报的信息能够体现在团级向师级指挥单元的汇报当中。假设相关任务的个体认知是相容的(compatible)[6],沟通实质上可以认为是实现认知的相互补充(compensation)。
个体认知的相互补充虽然能够促成系统认知的涌现[9],但不一定能获得一致的态势感知。因此,为了确保达成各Agent间一致的认知,本文在系统动态行为中引入反馈过程,通过反馈对彼此的认知进行校正,由此建立了DSA的一致性涌现的过程模型。如图1所示,在Agent进行个体认知的阶段,客观态势输入系统,经各Agent独自处理形成不同的个体认知;在团队协同阶段,Agent按照C2关系网结构所搭建的联系,彼此沟通并形成局部共享的认知。在反馈过程中,Agent分析局部共享认知,按照一定的一致性协议,调整自己的个体认知,从而缩小局部的认知差异。受到网络结构的制约,一致性协议只作用于网络上相邻的节点,仅能达成局部的一致性。但是,由于C2关系网是一个连通的整体,沟通使得局部一致性随时间的推进而逐渐扩散至全网,从而演变为全局的一致性,并最终生成全系统一致的态势感知。在反馈过程的参与下,上述一致性过程并非是一个线性过程,一致的态势感知也并非个体认知的简单叠加,而是Agent通过沟通、反馈而“涌现”形成系统特性。

图1 分布式态势感知的一致性涌现过程
总之,在DSA的一致性涌现过程中,Agent一边独立地实时更新个体认知,一边相互协同地进行沟通,经过反馈过程,系统对个体认知反复施加影响,通过一致性协议,逐渐形成局部到全局的一致的态势感知,整个过程涉及多个阶段,包含多种影响要素,是一个动态演化的过程。
1.2 一致性过程的动力学建模
一致性涌现过程是系统中Agent的集体动力学行为,由于每个Agent的行为过程相似,所以可以建立通用的Agent动力学模型。下面分别对个体认知阶段,团队协同阶段及反馈过程进行量化分析。
个体认知阶段的核心任务是处理客观态势并生成个体认知。从一致性分析的角度来看,我们并不关心每个Agent的感知的具体过程,而更关心Agent是否能够充分地感知客观态势并形成完整的个体认知,因此,可以将个体工作阶段看作一个简单的信息处理模型(如图2所示),从而定量分析输入与输出变量的关系。
客观态势输入到Agent的过程可以描述如下[10]:当C4ISR系统察觉到一个客观态势要素的变化超过一定的限度β(β>0)时,假设Agent认为这样大的变化足以引起新的决策行为,于是按照既定规则,C4ISR系统向Agent提供一条态势更新信息。如果C4ISR系统能够完全地捕捉客观态势变化,在信息域中,客观态势就可以映射为一连串的态势更新信息,而信息的数量体现了客观态势变化的快慢。

图2 分布式态势感知的一致性涌现过程
定义1 客观态势变化率:Agent在单位时间内收到的态势更新信息的条数,记为h(t)。
在分布式作战条件下,分散的地理位置会造成信息分发的时延,由于时延的差异Agent从C4ISR系统获取的态势信息,可能并不一致。但是,由于态势信息分发的耗时远远小于态势感知过程的耗时,在研究态势感知的一致性过程中,可以忽略态势信息分发的差异,认为个体认知的差异主要来源于Agent的态势信息处理能力。
定义2 态势信息处理能力:Agent在单位时间内能够完全感知的态势更新信息的条数,对于编号为i的Agent,记为ωi。它是Agent自身固有的态势感知能力,其大小取决于Agent自身的经验、能力。
当所有Agent态势信息处理能力相等时,由于系统中分发的态势信息并无差异、Agent感知过程相同,可以认为在认知域中,各Agent形成了一致的个体认知。因此,一致性分析并不需要涉及个体认知的具体内容,而关键在于建立个体认知与客观态势的定量关系。假设在足够小的时间间隔Δt内,Agent i完全感知的态势信息条数为ωi·Δt,态势信息的到达条数为h(t)·Δt,记Δt内Agent i自身认知增量为si(t),表示为

式(1)刻画了Agent对于当前态势的认知程度,有si(t)∈[0,1]。当态势信息处理能力小于客观态势变化率时,Agent只能部分感知当前态势,认知增量表示为需要认知的信息条数和能够认知的信息条数之比。反之,Agent能够完全感知当前态势,即使Agent的处理能力冗余,对客观态势的认知程度也不会超过1,故认知增量记为1。
定义3 个体认知:Agent i在某个时刻对于客观态势的感知结果,记为SAi(t)。在没有沟通反馈的情况下,个体认知完全依赖于Agent自身的态势处理能力,是自身认知增量累积的结果:

从式(2)可以看出,由于个体认知的动态累积特性,能力不同的Agent会形成有差异的个体认知,且随时间增长,差异将越来越大。一致性的达成依赖于团队协同阶段和反馈过程。
团队协同阶段的任务是沟通并形成共享认知,C2关系网的拓扑结构决定了沟通的对象。
定义4 C2关系网:军事组织中指挥控制相关单元(Agent)之间联系的抽象[1],用矩阵[cij]表示。若 A-gent i,Agentj间有联系(指挥关系,横向关系,执行关系),则认为其中有1条边相连,记cij=1;若Agenti,A-gentj间无联系,则cij=0。一般来说,传统的C2关系网为树状,而经由C2关系适应性构造出的C2关系网会呈现出无尺度、小世界等复杂网络特性[11-12]。
C2关系网虽然解决了与谁沟通的问题,但沟通只存在“有”和“没有”的区别,沟通过程中的差异没有得到有效的表达。从实际作战来看,由于作战单元间信任度不同,沟通应当具有不同的效果。因此,模型中A-gent之间的边应当具有不同的权值赋值。
定义5 沟通网络:Agent间沟通关系的集合,用矩阵表示记为[aij]。若 Agenti,Agentj间有沟通(双向),则aij> 0,aji> 0,aij、aji表示对沟通行为的信任程度。对于同一个沟通行为,Agenti,Agentj可能有不同的信任度,即可能存在aij≠aji的情况;若Agenti,Agentj间无沟通,则aij=aji=0。
沟通网络与C2关系网具有相同的拓扑结构,它是一个赋值的C2关系网,具体的赋值大小可以按照实际情况来进行设定。由于态势信息处理能力强的Agent往往是指挥控制中更为重要的节点,因此本文假设节点态势信息处理能力越强,则对于节点就可以越加地信任,由此定义Agenti对于相邻节点Agentj的信任度为

其中,Ni表示Agent i的邻居集合,di表示在C2关系网中Agent i的邻居个数(度数),ωj表示邻居Agent j的态势信息处理能力,μ为调节因子,μ用于调整信任的偏好程度,且 μ∈(0,1]。当 μ=1时,Agenti对所有邻居的信任度均为1,此时沟通无偏好,矩阵[aij]与[cij]相同;当0 < μ <1 时,Agent j的 ωj越大,aij也越大,表明Agent i偏好于信任节点态势信息处理能力更强的节点。随着调节因子μ趋向于0,Agenti对于强态势信息处理能力节点的偏好程度会越来越高,沟通的信任度也越来越不均匀。
沟通网络不仅描述了沟通的对象,还体现了沟通的差异,它是C2关系网在态势感知层面的拓展。在沟通网络的约束下,Agent形成局部共享认知,按照一致性协议反馈作用于个体认知。
定义6 一致性协议:Agent间相互作用的规则,表示为

其中,ci(t)表示Agenti按照一致性协议调整而获得的个体认知增量,Ni表示Agenti的邻居集合,aij表示信任度,ε表示Agent对于共享认知的接受度。在短时间内,Agent对于共享认知,不一定能完全理解吸收,因此将Agent对于共享认知的接受能力称为接受度,它刻画了相互作用的强度,设定ε∈[0,1]。从式(4)可以看出,Agent会根据邻居们的认知做出调整,使个体认知朝着趋于相同认知的方向演化。
在一致性过程中,Agent一边不断地对外界态势进行感知,一边通过沟通、反馈来调整个体认知,两者将共同推动个体认知的增长,因此,完整的个体认知增量由两部分组成:因个体态势信息处理能力而获得的增量和因一致性协议而获得的增量,表示为

此时,个体认知为

式(5)、(6)共同构成了Agent完整的动力学模型。
1.3 态势感知一致性的度量方法
态势感知一致性的度量方法建立在一致性过程分析的基础之上。从式(5)可以看出,系统并不存在绝对一致的态势感知。假设所有Agent个体认知完全相同,此时,因一致性协议而获得的增量为0,仅存在因个体态势感知能力而获得的增量si(t),由于不同Agent态势信息处理能力存在差异,Agent必然获得不同的个体认知,系统会重新呈现出不一致性。系统无法达到绝对一致的原因在于,Agent在态势认知过程中不断地引入差异。
尽管如此,系统仍然存在相对一致的状态。
定义7 相对一致状态:系统中Agent个体认知保持相对大小值稳定的差异,并以相同的认知增量δ(t)不断累积。相对一致状态是系统中Agent相互作用,相互牵制的结果,当Agent间差异不足以对决策行为产生影响时,也可以看作一致的态势感知。对相对一致性的度量包含三个指标:一致所需最短时间、系统内部一致性、外部一致性。
定义8 一致所需最短时间:系统达到相对一致性状态所需的最短时间,记作Tmin。
定义9 内部一致性:达到相对一致状态后,Agent间感知结果的差异程度,记作I,它表示为个体认知的均方差形式:

其中,V表示整个作战系统,n为系统中Agent的数量。内部一致性度量了Agent间沟通协调的能力。
定义10 外部一致性:达到相对一致状态后,A-gent对于外界态势的平均认知程度,记作O,表示为

外部一致性度量了系统对外界态势的认知能力。
上述指标从三个不同的方面度量了系统达成一致态势感知的能力(简称一致性能力)。对于某个特定的系统,在已知节点态势信息处理能力、沟通网络和相关参数的情况下,可以利用一致过程的动力学模型仿真计算出一致性指标,从而客观地度量系统一致性能力。

图3 沟通网络拓扑结构特性示意图(从左到右依次为层次型网络、随机型网络、无尺度型网络)
2 仿真分析
从式(5)可知,影响Agent动力学行为的因素包括:客观态势变化率h(t),态势信息处理能力ωi,沟通网络[aij]以及共享认知的接受度ε。由于动力学模型(5)、(6)无法直接求出解析解,下面通过仿真分析来研究不同因素对于系统态势感知一致性的影响。
仿真实验1:假设待研究的系统中Agent数量n=100,Agent的态势信息处理能力ωi按N(9,9)的正态分布取值,此时态势信息能力ωi落在(0,18)区间内的概率99.7%,它保证了ωi为正值。Agent间沟通的拓扑关系分别构成层次型(Hierarchy)、随机型(E-R)、无尺度型(Scale-free)的沟通网络(如图3所示)。取调节因子β=1,使沟通无偏好,取h(t)=18,使客观态势信息按固定速率到达,取接受度ε=0.1。设定仿真时间步为T=100,根据式(5)、(6)可以仿真计算系统中各个Agent的个体认知与个体认知增量,得到变化曲线如图4、图5、图6所示。

图4 层次型网络中个体认知增量δi(t)、个体认知SAi(t)随时间变化图

图5 随机型网络中个体认知增量δi(t)、个体认知SAi(t)随时间变化图

图6 无尺度型网络中个体认知增量δi(t)、个体认知SAi(t)随时间变化图
从上述各图可以看出,各Agent的个体认知增量曲线随时间逐渐收敛,个体认知曲线并非完全的发散状,而是呈一定的弧度逐渐聚集。这说明,在动力学模型的驱动下,Agent个体认知增量趋于一致,个体认知的差异逐渐稳定,系统能够达到相对一致的状态。但是,不同的网络结构使得系统一致性能力出现差异:一方面,随机型网络能够最快形成相等的个体认知增量,无尺度型网络稍慢,层次型网络最慢;另一方面,随机型网络个体认知的差异最小(曲线聚集最紧密),无尺度型网络较大,层次型网络最大。增加仿真时间步,可以得到具体的一致性指标如表1所示。

表1 各种网络的一致性指标对比
表1的数据说明,当时间足够长时,各类型的网络均能达到相对一致状态,且外部一致性O与网络结构无关。结合式(8)、(5)可知,在客观态势变化率一定的情况下,外部一致性由系统中各Agent态势信息处理能力和一致性过程确定。当Agent间沟通无偏好时(即调节因子β=1),一致性过程仅能够使Agent个体认知协调一致,而不会产生“新的认知”。因此,外部一致性为Agent平均态势信息处理能力ωi与h(t)的比值O=0.5,与网络结构无关。这也说明,无偏好的沟通虽然促成了系统的协调一致,但低能力与高能力Agent间平等交互、“各抒己见”,只能使系统达到平均的认知水平,而无法充分发挥高能力Agent的认知优势。Agent沟通偏好对一致性能力的影响将在实验六中详细分析。
对比表1中指标Tmin和I发现,层次型网络的指标值远远大于其他两类网络,且不在同一数量级。除了网络拓扑结构的差异外,层次型网络中的边数(Agent间的沟通数)也远远少于其他两类网络,是稀少的沟通导致了指标Tmin和I的巨大差异。因此,下面将通过仿真实验二、三分别研究沟通数量及拓扑结构对一致性的影响。
仿真实验2:假设待研究系统的Agent数为n=100,沟通关系构成层次型网络,其中任意一对未沟通的Agent间以概率p(0≤p≤1)形成新的沟通。随着沟通概率p的增大,网络中沟通数量越来越多,沟通范围越来越广。取与仿真实验一相同的参数,对p从0变化到1所生成的各个网络进行动力学仿真,纵坐标取对数坐标,得到指标变化如图7、图8所示。
需要说明的是,由于外部一致性O始终为0.5,没有作图表示。从图7、图8可知,当沟通概率p从0增大到0.2期间,指标Tmin和I呈指数减小,系统一致性能力迅速提升;而从0.2增大到1期间,指标Tmin和I缓慢减小,系统一致性能力变化不大。这说明,层次型网络与随机型、无尺度型网络在一致性能力上的巨大差异主要来源于沟通数量,稀少的沟通极大地限制了一致性的达成。另外,适当地增加沟通数量(例如,使p=0.2)可以迅速提升一致性能力,而一味地增加沟通数量并无益处,即沟通存在“饱和现象”。

图7 一致所需最短时间Tmin随沟通概率p变化图

图8 内部一致性I随沟通概率p变化图
对比图7、图8,可以看到一致所需最短时间与内部一致性具有相同的变化趋势。这是由于,个体认知的差异由个体认知增量的差异累积而来,个体认知增量收敛到一致所用时间越长,则差异累积的时间越长,就越不一致。因此,一致性所需最短时间会直接影响内部一致性,表现为指标I与Tmin相同的变化趋势。
仿真实验3:假设待研究系统中Agent数分别为n=100,200,300,…,1000,每一规模的系统分别构成随机型和无尺度型的沟通网络,并使网络平均度(网络中Agent平均沟通数量)相同。取与仿真实验一相同的参数,对上述各个网络进行动力学仿真,得到一致性指标变化如图9所示。

图9 一致所需最短时间Tmin随网络规模变化图
由于指标I与Tmin变化趋势相同,指标O始终为0.5,故不作图。从图9可知,一方面,随着规模的扩大,两类网络的一致所需最短时间Tmin增加,网络一致性能力下降。这是由于,扩大网络规模增加了Agent需要达成一致的对象数目,却并没有提升Agent间的沟通数(平均沟通数相同),相当于在信息传递能力固定的情况下,提高了信息传递的需求,使系统完成任务所需时间增加,一致性能力下降。
另一方面,随机型(ER)网络的一致性能力始终优于无尺度型(SF)网络,随着规模的扩大,随机型网络在一致性能力上的优势越来越明显。复杂网络理论[13]显示,无尺度型网络的节点度数呈幂律(Power-law)分布,这意味着少量节点的沟通数极大,而大多数节点沟通数极小,沟通数分布极不均匀;而随机型网络节点数呈泊松(Poisson)分布,节点沟通数较为均匀。在达成一致性的过程中,各Agent通过沟通首先形成局部一致的“簇”,无尺度型网络中的簇,以大度数节点为中心,簇内节点多,且大量节点沟通数极小,而随机型网络中,并无中心节点,簇内节点少,沟通数分布较为均匀。由前面的仿真实验可知,簇的规模越小、沟通数量越多,则簇越容易达成一致,因此,随机型网络比无尺度型网络容易形成局部一致的簇。由于全局一致由局部一致演化而来,随机型网络的系统一致性能力优于无尺度型网络。随着节点数增加,无尺度型网络独有的优先连接特性(preferential attachment)将使得大度数节点邻居数迅速增加,即簇的规模越来越大,导致无尺度型网络达成局部一致更加困难。因此,随着规模增长,随机型网络在一致性能力上的优势越来越明显。
仿真实验4:假设接受度ε从0变化为1,其余参数与仿真实验一相同,得到一致性指标变化如图10所示。

图10 一致所需最短时间Tmin随接受度ε变化图
由于指标I与Tmin变化趋势相同,指标O始终为0.5,故不作图。从图10可知,随着接受度ε增大,系统一致性能力逐渐增强,但当接受度大于某个值时,其个体认知增量δ(t)呈现出“震荡”现象如图11所示。
图11中,Agent个体认知增量绕δ(t)=0上下震荡,振幅随时间的推移而急剧增大,系统无法达到相对一致的状态。图10、图11说明,适当提升Agent对邻居节点个体认知的接受度,能够提升系统一致性性能,而当Agent过分地依赖于邻居节点时,自身个体认知被过度地修改,存在“矫枉过正”的现象,则系统无法达到相对一致。
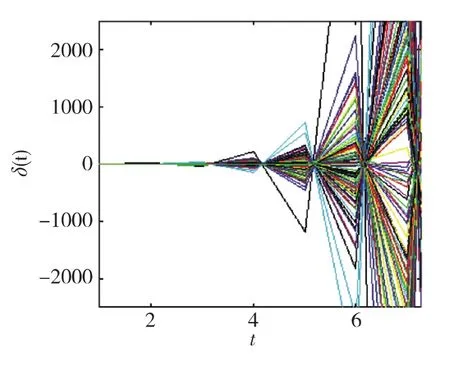
图11 个体认知增量δ(t)的震荡状态图
仿真实验5:假设客观态势变化率h(t)从0.2变化为20,其余参数与仿真实验一相同,得到一致性指标变化如图12所示。
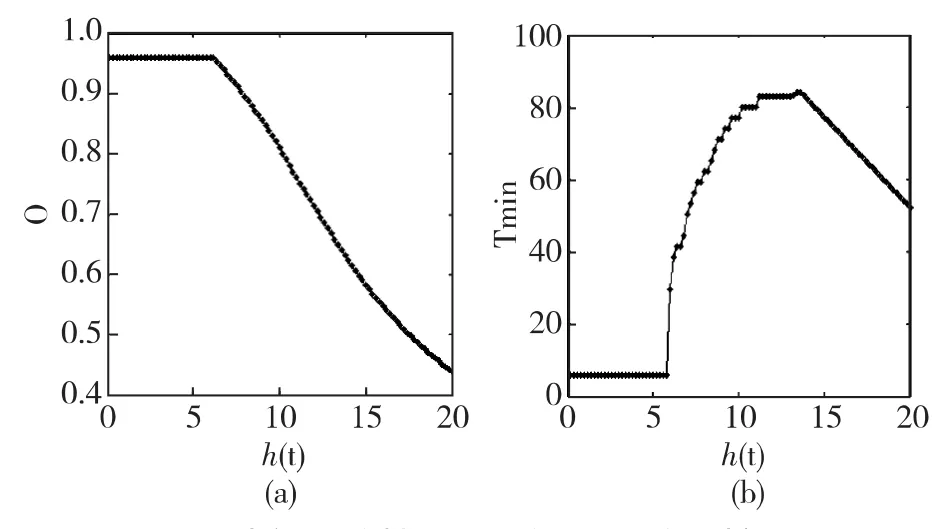
图12 外部一致性O、一致所需最短时间Tmin随客观态势变化率h(t)变化图
由于指标I与Tmin变化趋势相同,故不作图。从图12(a)可知,当h(t)<6时,O保持一定,说明当客观态势缓慢变动时,系统的认知程度能够保持的在较高的水平;当h(t)>6时,O随h(t)增大而逐渐减小,说明在系统认知能力一定的情况下,客观态势变化越快,系统认知程度越低。
从图12(b)可知,当h(t)<6时,Tmin保持不变;当6<h(t)<14时,Tmin随h(t)增大而增大;当h(t)>14时,Tmin和O随h(t)增大而减小。这是由于,当客观态势变化率h(t)很小时,绝大多数的节点能够完全感知当前态势,只有极少数的Agent有 ωi<h(t),因而 A-gent间个体认知差异不明显,Tmin保持不变。随着客观态势变化率h(t)增大,Agent态势信息处理能力ωi的差异开始凸显,个体认知增量 ωih(t)间的差异增大,使得Tmin增大。当h(t)超过某个值后,系统中Agent差异已经完全显现,而h(t)的增大使得 ωih(t)间的差异变小,反而使系统容易达成一致。即当客观态势变化速度过快的时候,系统中所有的Agent对于当前态势的认知都很“肤浅”,这反而缩小了个体认知的差异,有利于内部达成一致,故Tmin减小。
仿真实验6:假设调节因子μ从0调整到1,其余参数与仿真实验一相同,得到一致性指标变化如图13所示。

图13 外部一致性O、一致所需最短时间Tmin随调节因子μ变化图
由于指标I与Tmin变化趋势相同,故不作图。从图13可知,O、Tmin随μ减小而增大,说明使系统偏好于信任具有强态势信息处理能力的节点,虽然能够提升对客观态势的认知程度,但同时增加了达成一致所需最短时间,降低了内部一致性。当μ趋向于0时,Agent以强态势信息处理能力的节点的个体认知为标杆,不断地补充自身认知,这种“学习强者”的倾向提升了系统整体认知程度。但是,当Agent对邻居赋予不同信任度时,相当于对邻居进行了筛选,减少了沟通的数量,不利于系统内部各种认知意见的表达,故一致性指标O、Tmin受到影响。不过,适当地调整信任偏好(例如使μ=0.2),可以在少量影响指标O、Tmin的情况下,使得系统对于客观态势的认知程度得到提升,即系统存在使一致性能力最优的调节因子。
3 结束语
本文根据DSA理论的行为过程描述,从系统的角度,建立了一致性动力学模型和度量方法,并应用仿真计算验证了方法的有效性。仿真实验表明,适当地提高团队内沟通的广泛度和相互作用强度,选择合适的沟通网络,对提高一致性能力有积极的作用。
需要说明的是,本文在建模分析时附带了“网络传输的时延不计,客观态势变化率固定”的假设,为更加贴近实际的作战行动,下一步将考虑建立更具有一般意义的一致性分析模型。
本文提出的一致性分析与度量方法,可以让人们预先计算态势感知一致性差异的大小,并据此来设计恰当的多武器系统协同系统和与之相适应的指挥控制关系网络,以保证各类需要协同的系统能够正常运行,避免由于技术系统设计不当造成巨大损失。
[1]周道安,张东戈,常树春.C2组织指挥控制关系的形式化描述[J].指挥控制与仿真,2008,30(4):13-17.
[2]Lelyn D.Saner,Cheryl A.Bolstad,Cleotilde Gonzalez,Haydee M.Cuevas.Measuring and Predicting Shared Situation Awareness in Teams[J].Journal of Cognitive Engineering and Decision Making,2009,3(3):280-308.
[3]Perry W,Signori D,Boon J.Exploring Information Superiority:A Methodology for Measuring the Quality of Information and ItsImpacton Shared Awareness[R].Rand,2003.
[4]Yufei Shu,Kazuo Furuta.An Inference Method of Team Situation Awareness Based on Mutual Awareness[J].Cogn Tech Work,2005,7(4):272-287.
[5]Stanton NA,Ashleigh MJ,Roberts AD,Xu F.Levels ofAbstraction in Human Supervisory Control Teams[J].J Enterp Inf Manage,2006,19(6):676-694.
[6]Stanton NA,Stewart R,Harris D,et al.Distributed Situation Awareness in Dynamic Systems:Theoretical Development and Application of An Ergonomics Methodology[J].Ergonomics,2006,49(12-13):1288-1311.
[7]Rebecca Stewart,Neville A.Stanton,Don Harris,et ak.Distributed Situation Awareness in An Airborne Warning and Control System:Application of Novel Ergonomics Methodology[J].Cogn Tech Work,2008,10(3):221-229.
[8]Endsley M.R.Toward a Theory of Situation Awareness in Dynamic Systems[J].Human Factors,1995,37(1):32-64.
[9]Paul M Salmon,Neville A Stanton,Darshna Ladva,et al.Measuring Situation Awareness during Command and Control Activity:A Comparison of Measures Study[C],25thEACE,2007.
[10]孟辉,张东戈.连续态势变化条件下态势感知速度模型[J].系统工程与电子技术,2009,38(1):96-101.
[11]陶九阳,张东戈,孟辉.C2关系网络演化生成特性分析[J].指挥控制与仿真,2009,31(4):20-25.
[12]陶九阳,张东戈,赵普山.适应性指挥控制关系网的度分布研究[J].系统工程理论与实践,2012,32(8):1808-1813.
[13]汪小帆,等.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
