内次摆线用于无键联接

孙科， 卜睿

（陕西理工学院机械工程学院，陕西汉中723003）

0 引言

在机械的传动中，为了传递扭矩，很多情况下都会用到键联接。但对于传递很大的扭矩时，键联接会有如下缺点：1）轴上键槽的截面处容易产生应力集中，会引起轴的变形；2）当轴与轮毂配合后，由于轴孔的间隙，在高速回转中会产生离心力引起工作或生产中的振动；3）要相应地增大键槽段轴的直径，因此会增加材料的使用。鉴于以上情况，可以采用无键联接在某些场合中来取代键联接。基于内摆线的运动规律，考虑把轴的截面做成摆线的运动轨迹之一，即可以满足无键联接。

1 用于型面联接摆线截形的选取

当半径为r的动圆外表面内切半径为R的定圆内表面做纯滚动时，动圆上任意一点轨迹所组成的曲线就是内摆线。设动圆的自转角度为θ，公转角度为φ，选取动圆外表面上任意一点S为研究对象（S为一动点），可得出S点的运动轨迹的参数方程［1］为：

图1

式（1）为内摆线的参数方程，其中R为定圆半径，r为动圆半径。若把动圆外表面一点S移到动圆内部S1点处，此时S点到动圆圆心的距离就变为nr（其中0＜n＜1）。于是动圆内部任意一点的轨迹方程就可以写成：

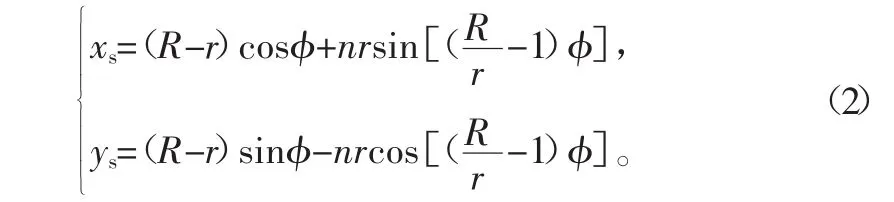
当n=1时，R/r的比值不同，得到的摆线形状也不同，当R=2r时得到的运动轨迹是一条直线，当R=3r、R=4r时得到的图形分别是三尖摆线和四尖摆线。

图2 当n=1时

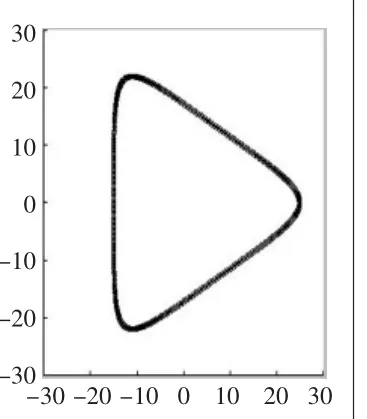
图3 当n=0.5时

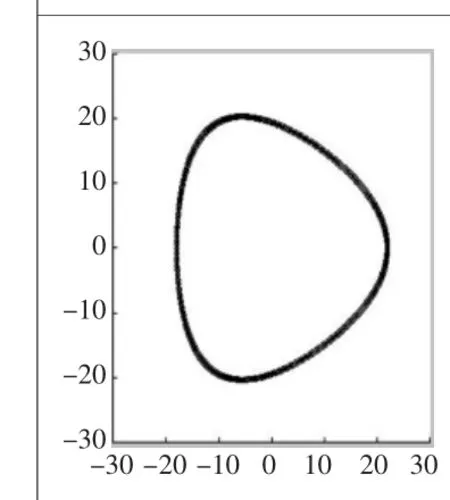
图4 当n=0.2时

图5 当n=0.1时

当n取不同值时，得到摆线在交结点处的平滑度也不同，为了满足研究的普遍性，取工业中最常见的三叶形作为型面联接的条件（即R=3r）。通过用Matlab软件的公式化绘图，图2～图5分别列出了 n=1、0.5、0.2、0.1时图形的对比。

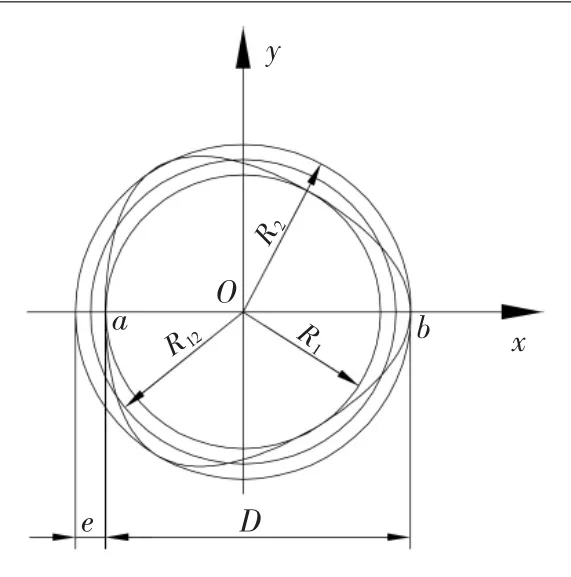
图6 摆线曲线

限于篇幅，n取0.7、0.8、0.4 等一系列值时，就不一一列出了。从图中可以看出摆线的形状在交结点处太“尖”或都太“平”，都不适合用于型面联接。经过与其它图形对比，最终选定n=0.2时的摆线作为型面联接的条件。

2 用Pro/E软件对型面进行三维建模

选取了R=3r、n=0.2条件下的内次摆线，由几何关系可以得出：

2）摆线轴公称直径D的确定。a、b两点分别为内切圆与外接圆上的点，令a点坐标（-rn+2r，0），b点坐标（2r+rn，0），由几何关系可得：

3）型面联接的三维建模。参考标准DIN32711-1979，选取空心摆线型面轴直径为45 mm的轴，其内径为20 mm，轮毂的外径为72 mm，当D=45时，由式（4）可得出r=11.25 mm，则由式（3）可得 e=2nr=4.5 mm。把 r=11.25，R=3r=33.75，n=0.2代入式（2）中，引入参数t（0≤t≤1）把式（2）中的φ变成tφ并输入到Pro/E的参数化表达式中，通过参数化建模描绘出摆线型面轴的截面形状，然后由“拉伸”命令拉伸50 mm高度得出摆线型面实心轴，再在摆线型面实心轴的中心打一个直径为20 mm的通孔，于是就得到了摆线型面空心轴。接下来建立联接型面空心轴的轮毂，首选在Pro/E的命令栏中点击“圆柱”命令，输入直径为72mm、高度为30mm的圆柱体，然后在圆柱体的中心打一个直径为e+D=49.5 mm的孔。把摆线型面空心轴装配到轮毂中，就得到型面联接模型图和三维实体模型，分别如图7和图8所示。

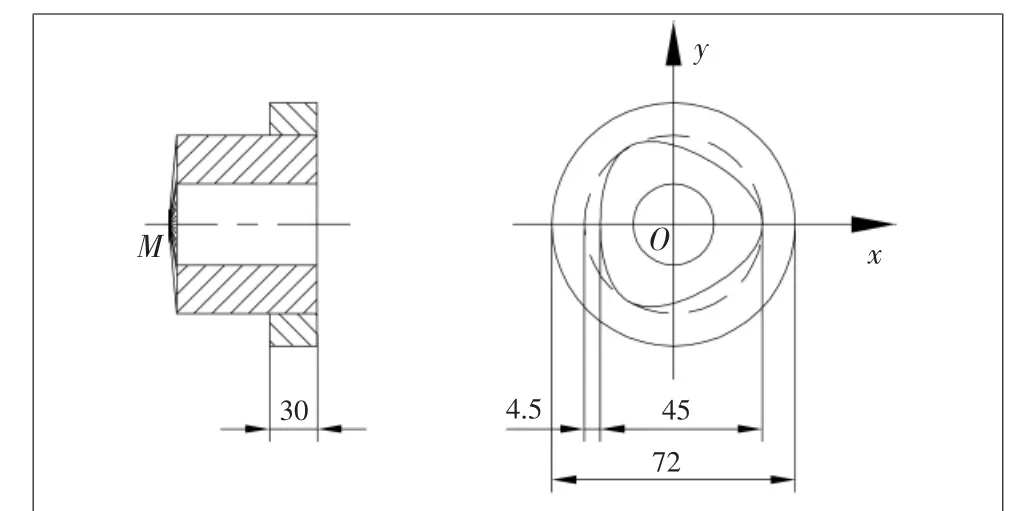
图7 型面联接模型的平面图

图8 三维实体模型

3 结论

作为机械传动中的联接方式，型面联接相对于传统的键联接相比，具有联接强度高、无应力集中等特点。可以用于传递扭矩轴的轴径很小、不适合在轴上开键槽的场合。并且型面联接可用于过盈配合、过渡配合，在负载和空载下都可以传递扭矩，适用于一些大型机械装备上，具有拆装方便及维修便利的优点。如果能够很好地解决型面联接的工作表面强化、定心问题，型面联接在机械的传动中的应用范围可以更广。

［参考文献］

［1］刘希玲，刘湘红.内摆线的平面运动［J］.长沙铁道学院学报，1998（3）：75-79.

［2］徐波.摆线的构成［J］.贵州大学学报，2001（8）：221-224.

［3］白海清，彭玉海，戴俊平.新型三尖摆线泵及其结构研究［J］.机械设计，2006（6）：16-17.

［4］王德胜，武良臣.三段弧等距型面的几何要素及其加工［J］.机械工艺师，1993（6）：12-14.

［5］刘春孝，王海燕.型面联接研究综述［J］.焦作大学学报，2008（3）：69-70.

［6］郭培全，赵萍，史锦屏.包络等距三边形型面联接研究［J］.济南大学学报，2004，6（2）：17-19.