Study on Internal Waves Generated by Tidal Flow over Critical Topography

JIA Xiaona, CHEN Xu,, LI Qun, and LI Qiang

1) Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266100, P. R. China

2) SOA Key Laboratory for Polar Science, Polar Research Institute of China, Shanghai 200136, P. R. China

3) Center for Ocean Science and Technology, Graduate School at Shenzhen, Tsinghua University, Shenzhen 518055, P. R. China

Study on Internal Waves Generated by Tidal Flow over Critical Topography

JIA Xiaona1), CHEN Xu1),*, LI Qun2), and LI Qiang3)

1) Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266100, P. R. China

2) SOA Key Laboratory for Polar Science, Polar Research Institute of China, Shanghai 200136, P. R. China

3) Center for Ocean Science and Technology, Graduate School at Shenzhen, Tsinghua University, Shenzhen 518055, P. R. China

Resonance due to critical slope makes the internal wave generation more effectively than that due to supercritical or subcritical slopes (Zhang et al., 2008). Submarine ridges make a greater contribution to ocean mixing than continental margins in global oceans (Müller, 1977; Bell, 1975; Baines, 1982; Morozov, 1995). In this paper, internal wave generation driven by tidal flow over critical topography is examined in laboratory using Particle Image Velocimetry (PIV) and synthetic schlieren methods in synchrony. Non-tidal baroclinic velocities and vertical isopycnal displacements are observed in three representative regions, i.e., critical, outward-propagating, and reflection regions. Temporal and spatial distributions of internal wave rays are analyzed using the time variations of baroclinic velocities and vertical isopycnal displacement, and the results are consistent with those by the linear internal wave theory. Besides, the width of wave beam changes with the outward propagation of internal waves. Finally, through monitoring the uniformly-spaced 14 vertical profiles in the x-z plane, the internal wave fields of density and velocity fields are constructed. Thus, available potential energy, kinetic energy and energy fluxes are determined quantitatively. The distributions of baroclinic energy and energy fluxes are confined along the internal wave rays. The total depth averaged energy and energy flux of vertical profiles away from a ridge are both larger than those near the ridge.

internal waves; critical topography; available potential energy; kinetic energy; baroclinic energy flux

1 Introduction

In the process of the ocean energy cascade, internal waves play a key role in momentum and heat transfer processes (Müller, 1977). When internal waves are generated from the interaction between barotropic tide and topography, they have the same frequency as the incident barotropic tide (Zeilon, 1912, 1934; Baines, 1973, 1982; Rattray, 1960).

Many studies have indicated that internal waves are non-ignorable sink of barotropic tide energy. Approximately 10% of the total barotropic tidal dissipation is transferred to internal waves (Bell, 1975), while only 0.3% is transferred to the continental margin. Hence, the bottom topography makes a greater contribution to the total energy conversion than the oceanic continental margin, by a factor of about 30 (Baines, 1982). Internal waves are one of the most important mechanic energy sources for deep ocean mixing and global thermohaline circulation (Munk and Wunsch, 1998; Garrett and Kunze, 2007). Consequently, it is of great significance to calculate the baroclinic energy and energy flux which are generated as tidal current flows over submarine ridges.

Balmforth et al. (2002) estimated tidal conversion using the Green function method. In their study, the conversion rate was related to topography and the ratio of the maximum topographic slope to the slope of internal wave rays. When the topographic slope approached or equaled the slope of internal wave rays, which was termed critical topography, the barotropic-to-baroclinic conversion rate became significant.

Let the angles of group velocity and topography relative to horizontal plane be α and β, respectively, then i) α>β corresponds to the subcritical case; ii) α<β the supercritical case; iii) α=β the critical topography. Previous experimental research on internal waves mostly focused on the subcritical and supercritical cases (Baines and Fang, 1985; Gostiaux and Dauxois, 2008; Peacock et al., 2008; Zhang et al., 2007; Lim et al., 2010; Dossmann et al., 2011). In this paper, experiments were designed to examine internal wave generation when tidal current flowed over critical topography. Zhang et al. (2008) studied the internal wave generation in a laboratory experiment of an oscillating tidal flow at the continental margin. Waves were generated only in the near-critical region, where the slope of the bottom topography matched that of internalwaves. Wang et al. (2012) did another experimental study on the relationship of and differences between the internal waves generated for two kinds of continental margins. In both studies, only the velocity field was measured and the density field was not provided. As a result, the available potential energy could not be calculated.

The resonance mechanism of critical topography enhances internal wave generation near the bottom (Zhang et al., 2008). This experiment studies internal wave generation under the critical condition. Since both sides of the isosceles triangle are the critical regions, it is adopted to simulate the submarine ridge terrain. Phase features of internal wave rays are analyzed individually. Finally, available potential energy, baroclinic kinetic energy, and baroclinic energy fluxes are calculated to analyze the energy transfer process.

2 Experiment Setup

Experiments were performed in a glass tank that is 500 cm long, 15 cm wide, and 40 cm deep (Fig.1). The tank, stratified to a depth of 25 cm, was filled with uniformly salt-stratified fluid using the ‘two-bank’ method (Hill, 2002), in which surface and bottom densities were 1005 kg m-3and 1025 kg m-3, respectively. Density decreased linearly with distance from the bottom of the tank so that the buoyancy frequency N is a constant,

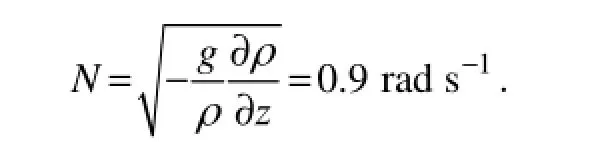
The tidal flow, U=Acos(ωt), was generated by a paddle wave maker with the amplitude A of 4 cm s-1and the frequency ω of 0.63 rad s-1. The data were not collected until the internal wave filed was well-developed (taking about seven periods of time). Besides, the horizontal scale of the topography is 22 cm, and the height is 11 cm, α=44˚, β=45˚.

Fig.1 Experiment setup. 1, Parallel light; 2, random dot pattern; 3, laser device; 4, glass tank; 5, topography; 6, computer; 7, camera.

Particle Image Velocimetry (PIV) (Ihle et al., 2009) and synthetic schilieren (Dalziel et al., 2000, 2007) were used to obtain horizontal and vertical velocities and density perturbation fields (Figs.2 and 3). Images captured by camera (AVT505B) with a resolution of 2452 by 2054 pixels were analyzed using Digiflow software, and the actual view size of the field is 55 by 46 cm. When the uniformly stratified fluid, characterized by a constant buoyancy frequency, N, flowed over topography, internal waves would be generated. The internal waves consisted of four internal wave beams radiating from the topography at an angle α to the horizontal plane under supercritical and critical conditions. All beams were tangential to the slope of topography.

Fig.2 Velocity field measured by PIV. Sections a–f are in the cross-beam direction and sections a1–a6 of the upward- and rightward-propagating wave beam.

The density fluctuation fields caused by internal wave rays are shown in Fig.3. The two beams radiating upward are stronger and more concentrated in isopycnal displacement fields than the other two. Owing to the fact that the tidal forcing is on the right hand side of topography, the internal wave beams on the same side are stronger than those on the other side. When internal wave beams radiate away from the ridge, the interior of the beams has a phase change. Internal wave beams are reflected when hitting the bottom of the water tank or the water surface, and the beam width greatly broadens after reflection. Here, if the center of the beam width is defined as where the maximum isopycnal displacement ζmaxof about 7 mm is located and the two boundaries are defined as where 15% of ζmaxis located, the upward- and rightward- propagating wave beam, as shown in Fig.3, has a width ofabout 12 cm (d2) after reflection, almost two times of that (d1～7cm) before reflection.

Fig.3 Density fluctuation fieldwith ten isopycnals(dark lines) from 1005 to 1023 kgm-3.

3 Temporal and Spatial Distributions of Internal Wave Rays

To analyze the properties of the four internal wave beams radiating from the topography with an oscillating tide flow over topography, critical (sections c and d), outward-propagating (sections a and b) and reflection regions (sections e and f) were selected in the cross-beam direction (Fig.2). Time series of horizontal baroclinic velocity u′, vertical baroclinic velocity w′, and isopycnal displacement ζ in sections a–f are shown in Fig.4. The baroclinic velocity perturbation is defined as

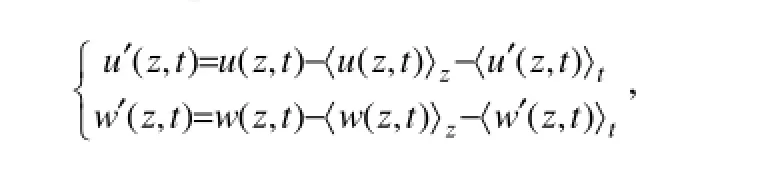
where u(z, t) represents the total tidal current velocity, the angle brackets〈〉trepresents the depth-dependent temporal average, and 〈〉zrepresents the depth integration, z is the water depth. The temporal and spatial distribution characteristics of u′, w′ and ζ, as well as the maximum values in each section, are summarized below:

1) Critical region: The horizontal baroclinic velocity u′in sections c and d was inphase, but the vertical baroclinic velocity w′ and isopycnal displacement ζ were outphase in the sections, respectively. The phase of ζ was approximately π/2 lagging behind w′. The influence of vortices generated by tidal flow over topography on internal wave structure was demonstrated by strong velocity fluctuations in section d (Fig.4).

2) Outward-propagating region: The phases of u′, w′and ζ in section a were all lagging behind those in section d. Likewise, the phases in section b were all lagging behind those in section c. Therefore, it can be concluded that the propagation path of internal wave rays generated on the left side of topography was from d to a. Likewise, the propagation path of internal wave rays generated on the right side of topography was from c to b to e.

3) Reflection region: Similar to sections d and f, sections b and e were synchronous with the phase of horizontal baroclinic velocity u′, but opposite in the phase of vertical baroclinic velocity w′ and isopycnal displacement ζ.

The phase of isopycnal displacement fields was approximately π/2 behind that of vertical baroclinic velocity fields in all above-mentioned sections, which is consistent with the properties of linear internal waves.

Focusing on the upward- and rightward-propagating wave beam, six cross-beam sections a1-a6 (Fig.5) were selected to study the temporal and spatial variations in the beam-propagating direction (Fig.2). As shown in Fig.4, the wave form in section a1 was greatly influenced by a vortex generated at the top of the topography. As a result, the wave beam became smoother and the initial beam width broadened, A similar beam widening was observed in an early numerical study of internal wave generation (Floor et al., 2011). However, when the wave beam was about to reach water surface, the beam width narrowed inthe beam propagating direction away from topography. This phenomenon was the result of energy loss at the surface and interaction with reflection wave beam.

Fig.4 Time series of u′ (red lines), w′ (blue lines), and ζ (dark lines) in sections a–f (from top to bottom).

Fig.5 Time series of isopycnal displacement fields ζ in sections a1–a6.

Because the direction of phase velocity is perpendicular to group velocity, both the phases of waves and the positions ofmaxζvary with time in the cross-beam direction (Fig.5).

4 Energy Transfer Characteristics of Internal Waves

Internal waves play a key role in ocean dynamics of energy transport from small to large scales. Available potential energy, baroclinic kinetic energy, and baroclinic energy fluxes in 14 time-averaged vertical profiles were calculated to study spatial variations of generation, outward-propagating, and reflection regions.

4.1 Baroclinic Energy

The potential energy, ρgz, is not a particularly useful quantity for studying internal waves. Therefore, the term‘available potential energy’ with more physical significance was introduced (Gill, 1982; Lamb, 2007). Assuming that the motion was in the x-z plane, Nash et al. (2006) gave the formulas for calculations of available potential energy and baroclinic kinetic energy as follows:

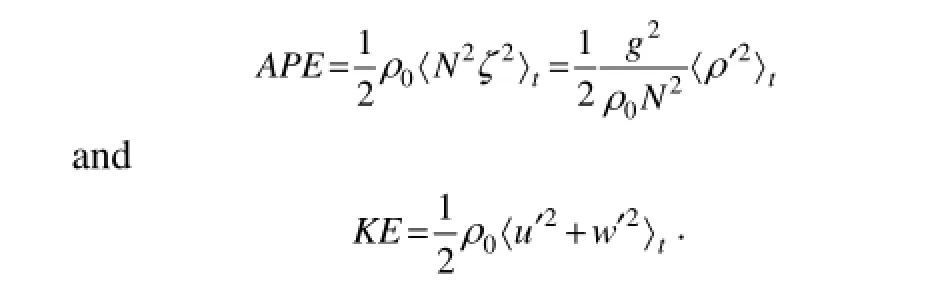
As shown in Fig.6, the maximum values of APE and KE appeared along the path of internal wave rays.

Because of the vortices generated by tidal flow over topography, the total energy in the sixth and seventh vertical profiles was less than that in other profiles (Fig.7). The total energy on the right side was stronger than that on the left side of topography due to the tidal forcing on the right.

4.2 Baroclinic Energy Flux

Profiles of isopycnal displacement, perturbation velocity, and pressure were used to estimate baroclinic energy fluxes (Fig.8)

The pressure anomaly p′ was calculated from the density anomaly using the hydrostatic equation

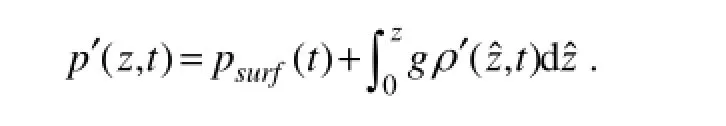
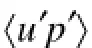
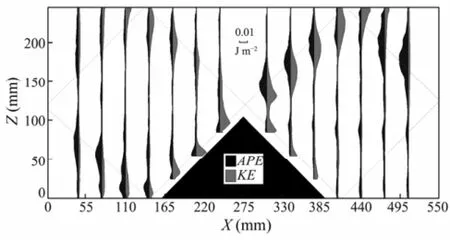
Fig.6 Internal wave energy in vertical profiles. APE (shaded dark), KE (shaded grey), and internal wave rays (dotted red lines).

Fig.7 Depth-integrated internal wave energy in vertical profiles.

Fig.8 Baroclinic energy fluxesin vertical profiles, left is negative and right is positive.

5 Conclusions

The laboratory experiments were conducted to investigate internal wave generation in this study. The research findings are as follows:

1) When a uniformly stratified fluid, characterized by constant buoyancy frequency, N, flows over topography,internal waves are generated, which consist of four internal wave beams radiating from the topography at an angle α, the slope of topography, relative to the horizontal plane.

2) The phase of each ray varies. For three feature regions–the critical, outward-propagating, and reflection region, internal waves are generated in the critical region and the phases of outward-propagating rays are all lagging behind that in the critical region. After reflection, rays are synchronous with the phase of horizontal baroclinic velocity u′, but out of the phase with vertical baroclinic velocity w′ and isopycnal displacement ζ.

3) The width of rays broadens first, and then narrows along the beam at a distance from the topography.

4) The maximum values of APE, KE and energy fluxes all occur on internal wave rays. The energy fluxes radiate outward from the critical topography, and total energy and energy fluxes away from topography are larger than those above topography.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 40906001 and 40906099), National 863 High-Tech Program (No. 2008AA09A402), and Chinese National Science & Technology Supporting Program (No. 2011BAC03B02-03-02).

Althaus, A. M., Kunze, E., and Sanford, T. B., 2003. Internal tide radiation from Mendocino Escarpment. Journal of Physical Oceanography, 33: 1510-1527.

Baines, P. G., 1973. The generation of internal tides by flatbump topography. Deep-Sea Research, 20: 179-205.

Baines, P. G., 1982. On internal tide generation models. Deep-Sea Research, 29: 307-338.

Baines, P. G., and Fang, X. H., 1985. Internal tide generation at a continental shelf/slope junction: A comparison between theory and a laboratory experiment. Dynamics of Atmospheres and Oceans, 9: 297-314.

Balmforth, N. J., Ierley, G. R., and Young, W. R., 2002. Tidal conversion by subcritical topography. Journal of Physical Oceanography, 32: 2900-2914.

Bell, T. H., 1975. Topographically generated internal waves in the open ocean. Journal of Geophysical Research, 80: 320-327.

Chang, M.-H., Lien, R.-C., Tang, T. Y., D’Asaro, E. A., and Yang, Y. J., 2006. Energy flux of nonlinear internal waves in northern South China Sea. Geophysical Research Letters, 33, L03607.

Dalziel, S. B., Hughes, G. O., and Sutherland, B. R., 2000. Whole-field density measurements by ‘synthetic schlieren’. Experiments in Fluids, 28: 322-335.

Dalziel, S. B., Carr, M., Sveen, J. K., and Davies, P. A., 2007. Simultaneous synthetic schlieren and PIV measurements for internal solitary waves. Measurement Science and Technolog, 18: 533-547.

Dossmann, Y., Paci, A., Auclair, F., and Floor, J. W., 2011. Simultaneous velocity and density measurements for an energy-based approach to internal waves generated over a ridge. Experiments in Fluids, 51: 1013-1028.

Floor, J. W., Auclair, F., and Marsaleix, P., 2011. Energy transfers in internal tide generation, propagation and dissipation in the deep ocean. Ocean Modelling, 38: 22-40.

Garrett, G., and Kunze, E., 2007. Internal tide generation in the deep ocean. Annual Review of Fluid Mechanics, 39: 57-87.

Gill, A. E., 1982. Atmosphere-Ocean Dynamics. Academic Press, New York, 662pp.

Gostiaux, L., and Dauxois, T., 2008. Laboratory experiments on the generation of internal tidal beams over steep slopes. Physics of Fluids, 19: 28-35.

Hill, D. F., 2002. General density gradients in general domains: the ‘two-tank’ method revisited. Experiments in Fluids, 32: 434-440.

利用地图数据、高速公路历史通行数据、历史假绿通车稽查数据和贵州省多义性拆分数据等，结合单出口嫌疑假绿通模型、货物地理嫌疑假绿通模型、卸货装货嫌疑假绿通模型和嫌疑假绿通车通行轨迹模型，通过大数据技术进行分析处理，筛选出嫌疑假绿通的车辆通行数据，并将其共享给稽查系统，辅助稽查工作人员快速定位嫌疑假绿通车辆。

Ihle, C. F., Dalziel, S. B., and Niño, Y., 2009. Simultaneous particle image velocimetry and synthetic schlieren measurements of an erupting thermal plume. Measurement Science and Technolog, 20, 125402, DOI: 10.1088/0957-0233/20/12/ 125402

Lim, K., Ivey, G. N., and Jones, N. L., 2010. Experiments on the generation of internal waves over continental shelf topography. Journal of Fluid Mechanics, 663: 385-400.

Lamb, K. G., 2007. Energy and pseudoenergy flux in the internal wave field generated by tidal flow over topography. Continental Shelf Research, 27: 1208-1232.

Morozov, E. G., 1995. Semidiurnal internal wave global field. Deep-Sea Research I, 42 (1): 135-148.

Müller, P., 1977. Spectral features of the energy transfer between internal waves and a larger-scale shear flow. Dynamics of Atmospheres and Oceans, 2: 49-72.

Munk, W., and Wunsch, C., 1998. Abyssal recipes II: Energetics of tidal and wind mixing. Deep-Sea Research I, 45: 1977-2010.

Nash, J. D., Kunze, E., Lee, C. M., and Sanford, T. B., 2006. Structure of the baroclinic tide generated at Kaena Ridge, Hawaii. Journal of Physical Oceanography, 36: 1123-1135.

Peacock, T., Echeverri, P., and Balmforth, N. J., 2008. An experimental investigation of internal tide generation by two-dimensional topography. Journal of Physical Oceanography, 38: 235-242.

Wang, T., Chen, X., and Jiang, W. S., 2012. Laboratory experiments on the generation of internal waves on two kinds of continental margin. Geophysical Research Letters, 39: L04602.

Zeilon, N., 1912. On Tidal Boundary-Waves and Related Hydrodynamical Problems. Almqvist & Wiksells.

Zeilon, N., 1934. Experiments on Boundary Tides: A Preliminary Report. Elander.

Zhang, H. P., King, B., and Swinney, H. L., 2007. Experimental study of internal gravity waves generated by supercritical topography. Experiments in Fluids, 19, 096602, DOI: 10.1063/ 1.2766741.

Zhang, H. P., King, B., and Swinney, H. L., 2008. Resonant generation of internal waves on a model continental slope. Physical Review Letters, 100 (24), 244504.

(Edited by Xie Jun)

(Received October 16, 2012; revised December 4, 2012; accepted May 21, 2014)

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2014

* Corresponding author. Tel: 0086-532-82031756

E-mail: chenxu001@ouc.edu.cn