LEP的风险损失估计分析与评价方法设计

2014-04-20卢朋

生产力研究 2014年5期

卢朋

（北京交通大学经济管理学院，北京 100044）

随着工程项目的复杂化、大型化趋势，传统管理模式不能适应大型复杂工程项目管理的需求，为了保障项目管理目标顺利实现，就需要综合运用风险管理方法与技术来组织项目管理，需要寻找与之相适应的新风险管理理念与模式。鉴于大型工程项目（Large Engineering Project，LEP）的特点，针对大型工程项目风险进行风险分析、风险评估和风险规避研究，有助于对大型工程项目风险分析，提高风险管理的有效性。

一、大型工程项目风险损失的评价思路

大型工程项目风险分析的目的是找出大型工程项目的实际结果与预期的目标的差异程度。工程项目风险不仅取决于事件发生的概率，并与事件发生后造成的影响程度有关。项目风险表示为风险事件发生的概率及其造成的后果的函数，可以用公示描述为：[1]

式（1）中：R为项目风险；p为该风险事件可能发生的概率；c为假设该风险事件发生会造成的影响和后果。

随着社会经济的发展，在大型工程项目建设过程中，复杂性工程的项目管理中不但施工技术风险和建设风险要素多，而且市场风险、管理风险大，如果控制风险不当，会带来极为严重的后果，因此须在项目早期进行风险预测和全周期的风险处置，须采取超前的管理理念来识别和规避全周期风险，且需要众多参与方和投资方共同承担项目风险。[2]基于LEP在风险上的多维特性，在参考项目风险发生概率和风险带来的影响和后果同时，风险的一些相关特性也需要给予关注：单个风险事件的可控程度、单个风险事件发生的可预测程度、风险若发生损失的转移性、分担性和保险性，把此类与风险有关的内容引入到风险管理和分析的程序中，会使决策者与风险分析人员对项目的风险具有更为系统全面的认识。为了方便分析，并且保证多维风险特性之间具有相互独立性，对这些方面进行归类与合并。一般可以总结为风险事件的可控程度（发生概率和带来的损失）、风险事件的可预测程度及风险损失的可转移程度三类（保险、分担等均可认为是转移的某个方法）。

针对风险事件分析新增的三个特点，反映了管理风险全周期过程中定性的知识或定量的信息，对风险管理与处理过程中的预测、控制与转移给予了考虑。所以，通过对风险五大特性的叙述，项目风险的定量信息与定性信息都将得到体现。在以后的分析中，还会发现，因为多维特性要同时处置定量与定性信息，所以要把两种计算与分析的方案相结合利用，恰好可补偿当前仅有模糊方法和概率方法的缺陷，凸显各自在方法分析上的优点。

因此，每个风险因素均考虑五方面的特征。给出以下多维特风险向量：

式（2）中：R为某个风险事件，r1，…，r5表示风险概率、损失、可预测性、可控制性、可转嫁性五个特性。

应该指出，对风险进行多维特性参考的条件下，对风险的估计和识别中也应该引入这些相应的内容。基于上述分析，要完成对工程项目各类风险事件的评估，应该考虑按照这样的思路步骤：依次进行风险因素的识别、风险的估计、风险概率分布的评价、风险损失大小的估计以及风险损失的综合评价。其具体思路过程，如图1所示。

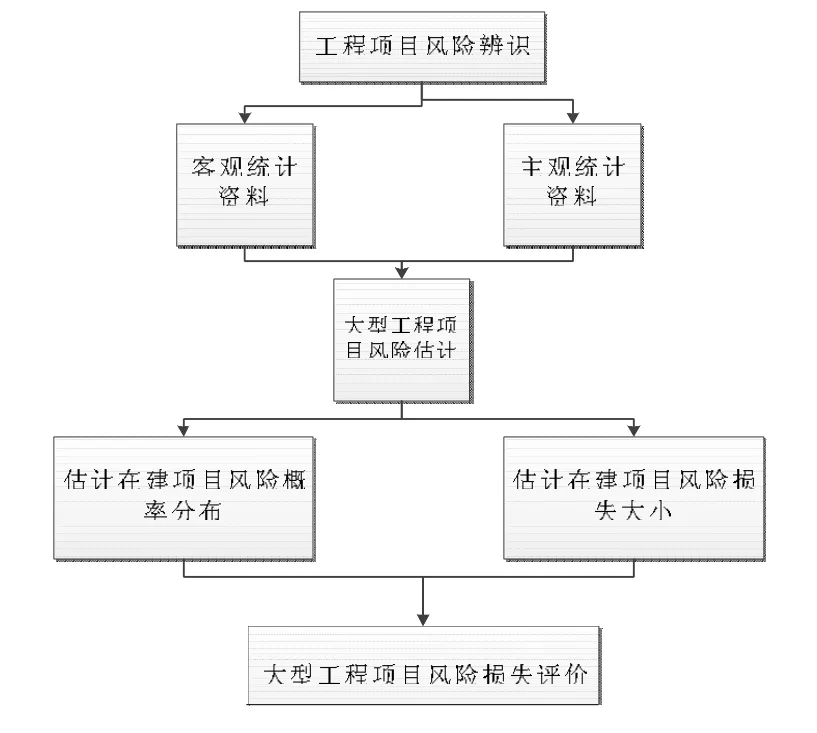
图1 大型工程项目的风险事件评估思路

二、大型工程项目风险损失的指标体系设计

大型工程项目一般建设周期长、规模大、涉及范围广、风险因素数量多、种类杂，在全生命周期内面临的风险多种多样。风险因素之间的内在关系错综复杂、风险因素之间并与外界交叉影响又使风险显示出多重的网络特性。项目风险管理（Project Risk Management）就是项目管理人员通过识别风险、对风险进行估计及评价风险，并基于此合理利用多种技术与管理手段对项目活动可能产生的风险进行有效控制，创造条件，主动采取行动，努力扩大风险带来的正面效应，尽力减弱或化解风险事件发生后带来的负面后果，以尽可能低的成本确保项目的整体目标可靠、安全地实现。项目风险管理的基础是对项目中的可能风险进行识别和预测。项目风险识别与预测包括以下方面：项目中可能风险因素的挖掘；风险因素分析与风险分类划分；风险事件影响程度判断。本文从大型工程项目的系统分析角度认为，大型工程项目风险损失的指标体系的设计，需要充分考虑在其建设施工过程中，来自各个方面的风险因素的干扰。这些风险因素来自投资管理的多元化、规模的大型化等诸多方面，基于大型工程项目的主要的风险因素的类别，将风险损失的指标体系分为五个方面。

（一）社会环境风险

社会环境风险包括政策、治安、文化素质等因素。政策法律的环境决定着大型工程项目的施工速度，某项政策的颁布或实施有可能影响项目的进展，社会治安环境、文化氛围、宗教习惯等都有可能对大型工程项目的实施过程产生影响。

（二）经济环境风险

整体经济环境和项目所在地区的经济发展状况都会给大型工程项目的实施和整体目标的实现产生影响，比如宏观经济环境趋势恶化、市场供求关系突变都会影响大型工程项目的资金、物料等，使得整个项目进度发生变化和调整。地方经济状况也会影响项目投资环境和服务水平。

（三）技术风险

大型工程项目的技术难度和复杂程度，决定了其实施过程中，技术方面的风险尤为突出，技术不够成熟可能会增加大型工程项目的测试时间和工作难度，对项目质量也可能存在一定影响，技术难度和复杂程度增加都会对大型工程项目的目标、质量和成本产生影响。

（四）自然灾害风险

自然风险是指由自然灾害而造成的风险，包括地质风险（如泥石流、滑坡等）、地震、气象风险（如飓风、强降雨等）等各种突发的自然灾害。

（五）管理风险

由于大型工程项目的参与方众多，管理层级和管理范畴复杂，某个管理方面的失误或者耽搁，都会对项目整体目标的实现产生影响。

大型工程项目风险损失的评价指标体系，如图2所示。

图2 大型工程项目风险损失的指标体系

三、大型工程项目风险损失的估计模型

基于大型工程项目风险损失的特征，为全面分析项目风险的概率和影响程度，按照平衡损失函数，设计大型工程项目风险损失的估计模型。

（一）平衡损失函数

从统计判决的理论角度看，就是在二次损失函数（d-β）'（d-β）下，选取了使风险值达到了最小的估计。

Zellner提出了Zellner平衡损失函数的判定标准，基于此标准，综合最小二乘法估计方法和损失函数，形成以下标准：

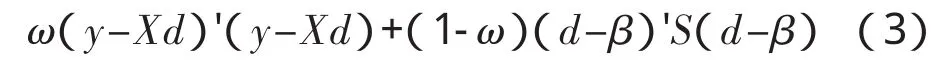
其中0≤ω≤1，S为已知正定阵。

基于Zellner平衡损失函数的风险损失判定标准式（3）首先把估计精度的优良性纳入到判定标准中，突出了模型在拟合度上的优良性。对判定大型工程项目相对复杂的风险因素来说，这是比较全面、相对合理的标准。该平衡损失函数判定标准的第一部分是线性模型的残差，对应的就是经典的最小二乘估计，表述了参数估计β＾对整个平衡损失函数的拟合优良度；第二部分则是关于参数精度的优良性，在损失函数MSE（β＾）下选取使得风险达到最小的估计。

其中X0：p×n和V>0已知，θ∈RP和σ2＞0均为未知参数。设C为k×p阶矩阵，Cθ可估，取（d-Cθ）'（d-Cθ）和线性估计类L={L Z：L为k×n阶常数矩阵}，则L Z在线性估计类L中是Cθ的容许估计的充要条件：[3]

由此，我们可以得出如下推定：

根据Gauss-Markov模型和Zellner平衡损失函数的含义，LY是β的在线性估计类L中的线性容许估计全体所组成的一个集合，A*是在Zellner平衡损失函数判定标准（3）下，β在线性估计类L中的线性容许估计全体组成的另一个集合，据此则有：

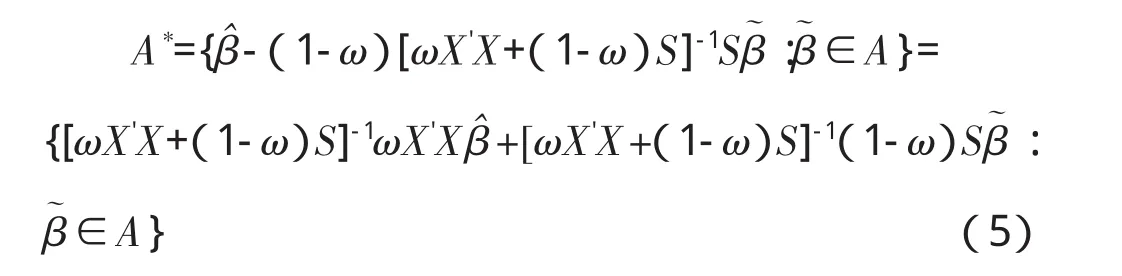
所以说，作为兼有拟合优度和精度的平衡损失函数，其线性容许估计是拟合优度和精度下的线性容许估计的平衡。

根据平衡损失函数的定义，相关风险函数为：

R（β，σ2；L）=E[ω（Y-XLY）'（Y-XLY）+（1-ω）（LY-β）'S（LY-β）]=ω[σ2tr（IP-XL）（IP-XL）'+β'X'（IPXL）'（IP-XL）Xβ]+（1-ω）[σ2trSLL'+β'（LX-IP）'S（LX-IP）β]

一般来说，为了计算方便我们取S=I。

（二）基于平衡损失函数的LEP风险贝叶斯估计

基于以上分析，大型工程项目的项目风险估计主要是运用概率统计等方法对特定的不利事件的发生概率以及风险事件发生所造成的损失进行定量估计，尽可能用量化的数据来分析风险事件，从而对风险管理提供技术参考指导；同时，大型工程项目的风险事件的概率估计，因为风险事件因素构成复杂，数据资料通常不足或无法获取全面精确的预测信息，需要应用先验概率来给予统计处理。经验分析知道，先验概率通常具有太多的不确定性，需通过一定的统计或计算方法来获得补充信息，以完善先验概率。这种通过对项目进行更多、更广泛的调查研究或统计分析，再对项目风险进行估计的方法，称为贝叶斯概率法。[4]

贝叶斯概率法所对应的贝叶斯线性无偏最小方差估计（BLUMV）解为：

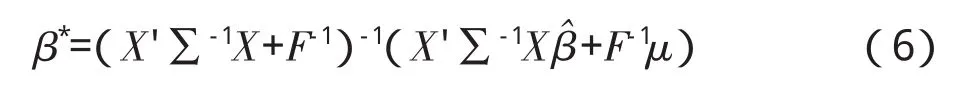
而在平衡损失函数下的估计解为：

其中，μ为常数向量，F>0为已知的正定向量。

在Gauss-Markov模型和平衡损失函数[5]下，BLUMV优于β最小二乘估计的充分必要条件是ϖ<0.5。

四、基于蒙特卡洛的LEP风险评价分析

蒙特卡洛方法是以概率统计理论为基础的一种方法，与事件数、事故数等安全分析方法相比，蒙特卡洛方法可以对未知事件带来的影响进行仿真，把工程项目在各个可能方案下风险损失评价指标的特征值定量地进行描述。通俗地说，蒙特卡洛方法是用随机试验的方法计算积分，将所要计算的积分看做是服从某种分布密度函数的随机变量的数学期望，通过模拟各种变量间随机变化的动态关系，并根据风险概率来确定一定置信区间下的模拟次数，模拟结果可以很好地描述项目过程。借用蒙特卡洛方法来帮助工程项目风险决策，在近些年的实际项目开发中已有一定的应用，主要在不确定环境下，通过计算一系列的相关评价指标值，根据模拟计算结果，从而为项目决策管理提供相应量化依据。

大型工程项目风险损失评价中各参与变量如政策环境、技术风险、管理风险等影响因素都存在一定的不确定性，而风险变量一般都是同时发生变化，给线性计算、单次仿真带来难度；根据大型工程项目风险损失评价的计算公式，计算LEP关于NPC值就是一个风险损失评价分析的过程。本文建立的分析方法优势在于，首先，能够根据相关文献及初始分析为风险变量进行假设可能，为其选择合理的初始值，符合项目管理的实际情况；其次，针对各变量具备不同的分布特征这一情况，为每个风险变量因素分别设定各自的概率，这样充分考虑了影响内部净现值（NPV）的各因素的随机性，从而得出符合风险损失分析实际情况的评价值。

蒙特卡洛估计NPV的流程如下：[6]（1）基于平衡损失函数确定NPV的函数；（2）对LEP的风险影响因素进行分析，并选取主要影响因素；（3）确定分析的目标函数；（4）对各要素进行随机抽样；（5）在对项目风险定性分析基础上确定因素的初始值；（6）产生一组随机参数组合，代入计算公式，求出一个目标函数值；（7）返回第（6）步，反复计算N次；（8）N次计算完成后，得到目标函数的期望值、方差等系列统计指标；（9）计算与分析。

计算LEP风险用下式：

Er=σn/ENPV

式中，Er为LEP风险；σn为均方差；ENPV为NPV的期望值。

某大型工程项目具体的财务评价数据如表1所示，并设定建筑业行业基准折现率为15%。

根据上述变量变化及概率分布情况，结合建立的基于Zellner平衡损失函数判定标准的LEP风险贝叶斯估计，按照蒙特卡洛模型方法的思路，进行至少10 000次模拟计算，输出一系列配套随机数据，得出该大型工程项目NPV的概率分布情况。本文采用Crystal Ball软件，得到某大型工程项目净现值分布图、净现值概率表以及净现值统计表，其结果如图4、表2、表3和表4所示。

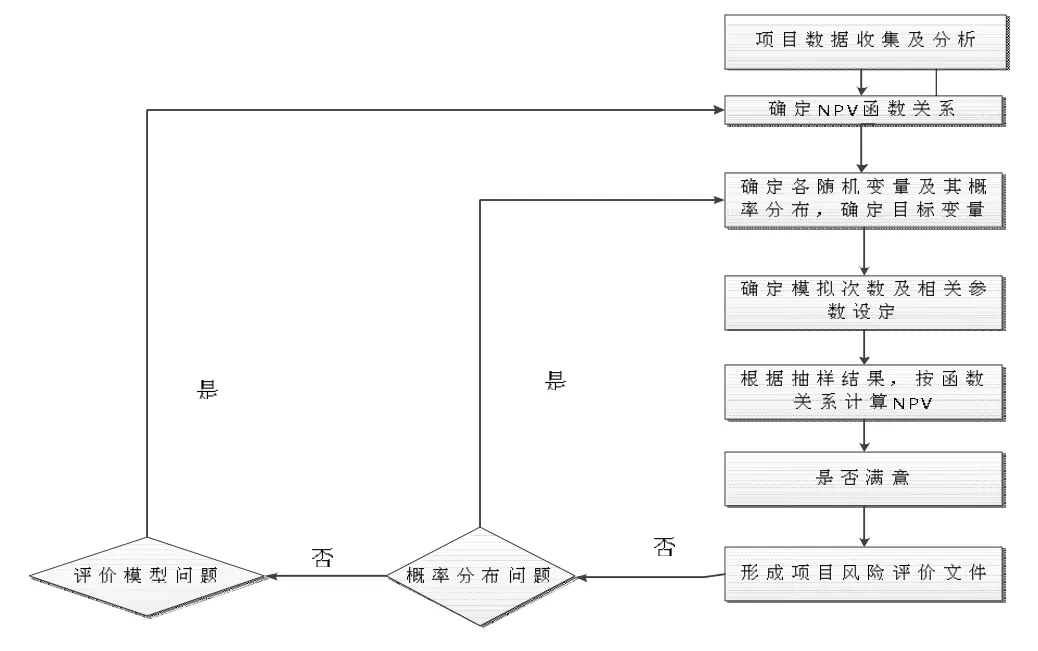
图3 基于蒙特卡洛的LEP风险评价分析

表1 大型工程项目主要技术经济指标

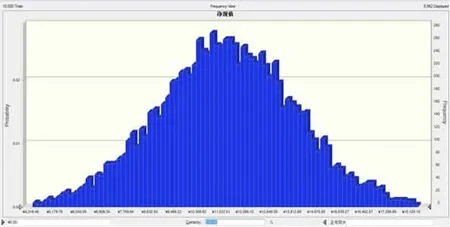
图4 大型工程项目净现值样本分布图

表2 大型工程项目净现值统计表（10 000次模拟运算）

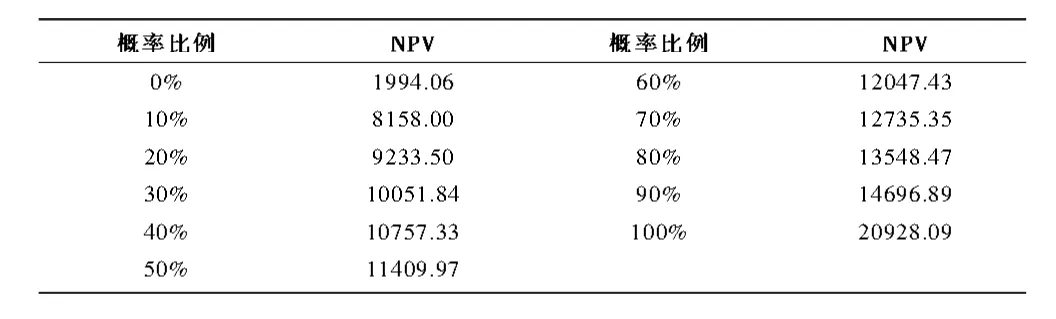
表3 大型工程项目净现值百分位数表（10 000次模拟运算）

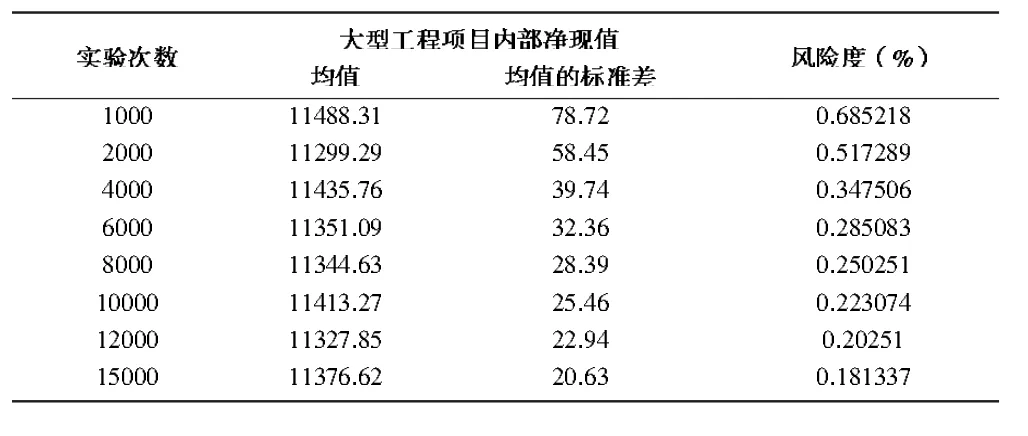
表4 大型工程项目风险度计算

由以上运行结果可知，经过10 000次模拟后，NPV的指标逐步呈现收敛特征。净现值的平均值为11 413.27万元，最大净现值为20 928.09万元，最小净现值为1 994.06万元；由表4可知经过10 000次模拟运算后，净现值的分布有70%的概率达到在12 735.35万元，项目净现值小于零的概率为零，实现盈利的概率为100%，LEP风险度为0.223 1%。因此得出结论，盈利机会高且大，风险度极小，说明该项目可操作性很强。