基于动态面法的导弹制导控制一体化设计方法研究
2014-04-19马文桥何晨迪马国强
马文桥,何晨迪,史 震,黄 晗,马国强
(1.哈尔滨工程大学自动化学院,哈尔滨150001;2.北京机电工程研究所,北京100074;3.哈尔滨建成集团有限公司,哈尔滨150030)
基于动态面法的导弹制导控制一体化设计方法研究
马文桥1,何晨迪1,史 震1,黄 晗2,马国强3
(1.哈尔滨工程大学自动化学院,哈尔滨150001;2.北京机电工程研究所,北京100074;3.哈尔滨建成集团有限公司,哈尔滨150030)
摘要:为避免传统导弹制导和控制系统单独设计存在的缺陷,将两个系统综合考虑,提出一种制导控制一体化设计方法。首先推导出俯仰通道的制导控制一体化数学模型,并化为级联形式;然后引入动态面方法并结合非线性干扰观测器技术,提出了一种基于非线性干扰观测器的积分动态面一体化制导控制系统设计方法,在每一个子系统设计时引入误差的积分项以消除稳态误差,提高了子系统的跟踪精度;采用Lyapunov函数对系统稳定性进行了分析;最后通过仿真验证了所提出的一体化控制算法的有效性。
关键词:制导控制一体化;动态面;反步法
Key woorrddss:Integrated guidance and control;Dynamic surface;Backstepping
0 引言
采用传统方法进行导弹制导控制系统设计时,一般将制导系统和控制系统分别进行设计,然后再将两个系统合到一起进行调试[1]。之所以采用这种方法是由于控制回路的带宽远大于制导回路的带宽(一般为5倍以上),因此将控制回路视为快回路,制导回路视为慢回路,基于频谱分离的原理,可以将两个系统分别进行设计[2]。这种假设在一般情况下是成立的,但是在导弹末制导段,随着弹目相对距离的缩小,制导回路的时间常数将变小,带宽也随着变大,此时这个假设将不再成立,因此采用传统方法设计的控制系统精度难以达到要求,并且整个系统需要进行反复调试[3]。
制导控制一体化设计方法将制导系统和控制系统视为一个整体,根据弹目相对位置信息和导弹自身的运动状态信息,直接产生导弹的控制指令[4],因此一体化设计方法不依赖于上述假设,即使在导弹和目标较近时,也不会出现太大的制导误差,近几年得到较大关注[5-7]。
由于一体化数学模型较为复杂,并且复合控制导弹存在较大的干扰项,因此控制系统是一个带有较大参数不确定的非线性系统。
本文将采用反步法的基本思想,将整个制导控制一体化数学模型分解为几个相互联系的子系统进行设计,并针对传统反步法存在的缺陷进行改进,采用动态面技术,避免“计算膨胀”的问题;对模型中存在的不确定项,采用非线性干扰观测器进行估计;另外在子系统跟踪误差设计时,参考传统PID控制的思想,引入误差积分,重新定义了误差量,从而消除跟踪中存在的稳态误差。最后在某特征点对导弹进行了仿真验证。
1 制导控制一体化数学模型
考虑滚转稳定导弹在末制导段的拦截问题,俯仰和偏航通道之间的耦合较小,且两个通道的数学模型类似,因此本节以俯仰通道为例,研究导弹和目标在铅垂面内的相对运动。俯仰通道弹目相对运动关系如图1所示。
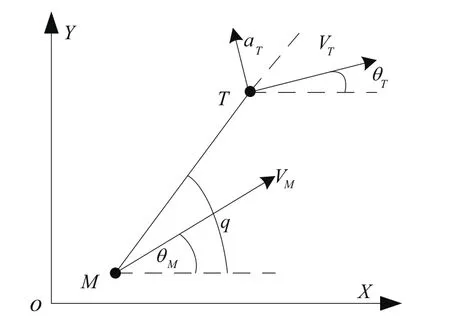
图1 弹目相对运动关系Fig.1 Dynamics between missile and target
根据俯仰平面内的弹目相对运动关系,可得导弹和目标在沿着视线方向及垂直于视线方向上的相对运动学方程分别为:

对式(2)求导,并将式(1)代入得:

假设导弹和目标进行机动时只有速度的方向发生改变,而速度的大小保持不变,即式(3)中V.T=V.M=0,并令Vq=Rq.表示导弹垂直于视线角方向上的速度分量,aT=VTθ.T、aM=VMθ.M分别表示目标和导弹法向加速度大小,则式(3)可进一步化简为:

根据文献[8],有以下关系:
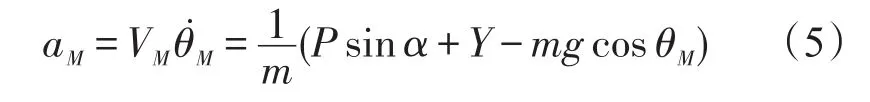
将式(5)代入式(6)可得:
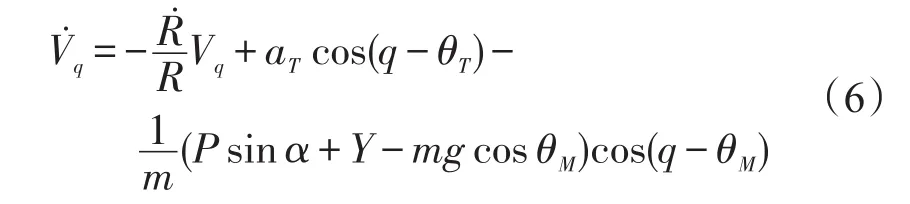
以下两式成立:

其中,升力Y及俯仰力矩Mz分别表示为:

假设末制导段推力P=0,忽略舵面产生的升力,视线角与弹道倾角近似重合,即q-θM≈0,并将目标机动、通道间耦合、喷流干扰导致的气动参数变化以及方程简化过程中忽略的小量所产生的影响全部视为外界扰动,得到如下简化的制导控制一体化数学模型:

式中, ΔVq、 Δα、 Δωz为模型中的不确定干扰,为有界函数,且假设、、也是全局有界的。
式(14)所示的一般形式[9]:

式中,系统的输出为 y=x1;控制量为 u;d1(x2), d2(x2), d3(x2,x3,u)为不确定干扰引起的建模误差项;其余各项分别为:

可以看出,该系统是一个带有不确定性的具有级联形式的非线性系统,且d1,d2是非匹配不确定部分,d3是匹配不确定部分。控制系统设计的目标就是令状态变量x1收敛至0,即令视线角转率趋于零,且对系统中存在的不确定性具有良好的鲁棒性。
2 制导控制一体化设计
基于平行接近法的思想,为保证导弹能够准确拦截目标,只需使导弹在末制导段最后时刻的视线角转动速度q.能够趋于0即可。因此对于制导控制一体化数学模型,只需保证x1→0,同时保证导弹攻角和俯仰角速率保持稳定即可使导弹精确命中目标。本节将用动态面反步法设计一体化控制系统。
第一步:考虑系统式(14)中的第一个子系统(14–a)。首先定义(14–a)子系统的跟踪误差:

式中,x1d为闭环系统(14)的期望指令信号。
根据自动控制理论可知,当系统存在未建模动态或外界不确定干扰时,系统会存在稳态误差,PID控制方法通过引入积分控制来消除稳态误差,以提高系统的鲁棒性。因此为消除(14–a)子系统的稳态误差,借鉴PID控制的思想,引入跟踪误差z1的积分项,构造一个新的误差信号[10]:
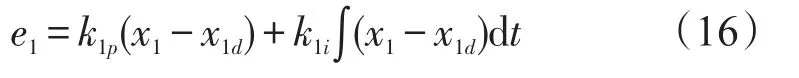
式中,k1p,k1i为调节参数,分别对应于PID控制中的比例系数kp及积分系数ki。通过构造新的误差信号e1,能够保证(14–a)子系统的跟踪误差z1能够无稳态误差地收敛于0,提高了系统的跟踪精度。
为(14–a)子系统构造正定的Lyapunov函数V1:

对Lyapunov函数V1求导得:

将x2看成是(14–a)子系统的虚拟控制量,设计为:

式中,k1>0为设计参数;ˆ为(14-a)子系统不确定项d1的估计值,采用如下形式的非线性干扰观测器求得:

式中,l1为观测器增益,z1和p1为中间变量。
定义第一个干扰观测器的观测误差为:

由干扰观测器原理可知[11],存在l1>0,使得ε1=l1ε1,从而使得(14–a)子系统的干扰观测误差是全局稳定的。
此时Lyapunov函数V1的导数为:

因此,根据Lyapunov稳定性定理,子系统是稳定的。
根据动态面法的基本原理,令x2通过一个时间常数为τ1的一阶低通滤波器,产生x2d,这样在第二个子系统(14–b)设计的时候,只需用滤波器的估计值x2d代替设计的虚拟控制量xˉ2,避免了反步法中对虚拟控制量的求导操作。滤波器设计为:

第二步:考虑系统(14)中的第二个子系统(14–b)。将x3看成是(14–b)子系统的虚拟控制量,采用同样的方法构造一个新的误差信号e2和正定的Lyapunov函数V2,将虚拟控制量设计为:

式中,k2>0为设计参数;为(14–b)子系统不确定项d2的估计值,采用如下非线性干扰观测器求得:
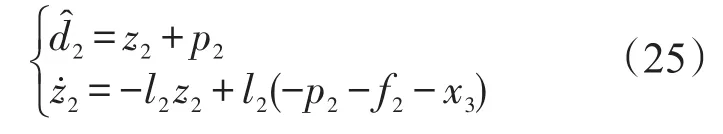
式中,l2为观测器增益,z2和p2为中间变量。
与上一步类似,令x3通过一个时间常数为τ2的一阶低通滤波器,产生x3d,代替设计的虚拟控制量xˉ3。滤波器设计为:

第三步:考虑系统(14)中的第三个子系统(14–c)。按照同样的方法构造新的误差信号e3和正定的Lyapunov函数V3,设计出系统的实际控制量:

式中,k3>0为设计参数;为(14–c)子系统不确定项d3的估计值,采用如下形式的非线性干扰观测器求得:
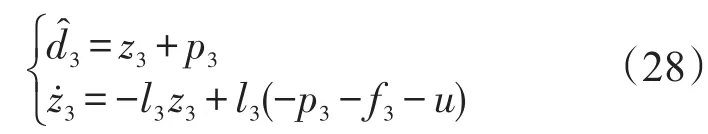
式中,l3为观测器增益,z3和p3为中间变量。
3 稳定性分析
定理1:对于系统式(14),采用如式(27)控制量,如式(19)、(24)的虚拟控制量、如式(20)、(25)、(28)的干扰观测器、如式(23)、(26)的低通滤波器,可以使整个系统渐进稳定,并且其中每个子系统都是渐进稳定的。
证明:制导控制一体化系统式(14)中的每个子系统的稳定性通过构造Lyapunov函数V1,V2,V3已经得到了证明。下面主要证明整个系统的稳定性。为此,首先将上一小节中的几个误差变量整理成一般形式,定义三个误差变量。
定义第i (i=1,2,3)个子系统在引入积分项后,新构造的误差为:

定义第i (i=1,2,3)个干扰观测器的观测误差为:

由干扰观测器原理可知,存在li>0 (i=1,2,3),使得 εi=liεi(i=1,2,3),从而使得第i (i=1,2,3)个子系统的干扰观测误差是全局稳定的。
定义第i (i=1,2)个滤波器的误差为:

对式(31)进行求导得:

由滤波器动态方程得:

将式(33)代入式(32)中得:
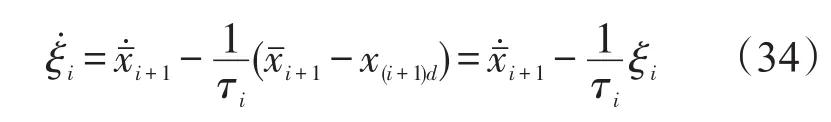
为系统(14)构造如下的Lyapunov函数:

将上式的Lyapunov函数对时间t求导得:

假设指令信号及一阶、二阶导数存在且有界,则根据表达式(23)、(26)可知,存在有界函数δi+1>0, (i=1,2), 使 得, 令 δmax=max{δi+1}, (i=1,2),则:
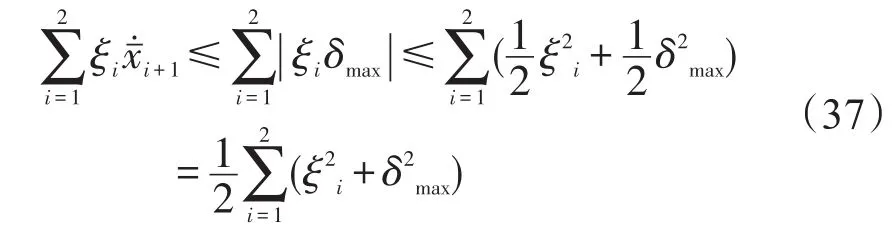
将式(37)代入式(36)得:

由式(38)可知,可以通过设计合适的参数,使得c0>0,且满足c0>c1/V(0),V(0)为Lyapunov函数V的初始值,此时满足V.<0。因此Lyapunov函数V有界,且所有信号有界,所以采用本文设计的一体化控制律uc作用下,制导控制一体化系统的所有误差信号都可以收敛至原点附近任意小的邻域。
证毕。
4 仿真实验与结果分析
为了验证本章设计的一体化控制算法的有效性,本节将在Matlab/Simulink环境下对导弹末制导段进行数学仿真,假设从末制导开始时刻起,目标进行幅值为10g、周期为2s的正弦机动:aT=10g·sin(πt);导引头制导盲区设为100m,当弹目相对距离小于该值后,制导控制系统停控,导弹依靠惯性飞向目标;舵机近似传递函数为:G(s)=1/(0.03s+1),且限幅为±30°;为保证弹体稳定,导弹的攻角需满足:|α|≤20°,同时俯仰角速度需满足:|ωz|≤200(°)/s。
仿真曲线如图2-图5所示:

图2 视线角速度变化曲线Fig.2 Curves of LOS rate

图3 攻角变化曲线Fig.3 Curves of attack angle

图4 俯仰角速度变化曲线Fig.4 Curves of pitch rate

图5 舵偏角变化曲线Fig.5 Curves of elevator deflection angle
图2所示为导弹的视线角速度变化曲线。可见一体化控制器能够使视线角速度迅速收敛至0附近,并且在末制导遭遇段仍能保持稳定不发散,从而保证导弹不会因目标机动而脱靶;而采用比例导引时视线角速度收敛较慢,收敛过程随着目标机动存在较大的波动,并且在即将遭遇目标时,随着相对距离的减小有发散的趋势,无法保证导弹精确拦截目标。
图3所示为导弹的攻角变化曲线。可见两种设计方法得到的导弹攻角均能满足物理条件限制,从而保证姿态稳定;采用一体化控制器得到的导弹攻角变化更为平稳,且在大部分飞行阶段,其攻角都小于制导与控制分开设计。
图4所示为导弹的俯仰角速度变化曲线。可见末制导在初始阶段,为消除导弹的初始指向误差,导弹的俯仰角速度变化较大,但两种设计方法得到的导弹俯仰角速度均能满足限制条件;随着弹目的接近,采用一体化控制器得到的俯仰角速度变化比较小,而采用传统方法设计的导弹俯仰角速度则相对较大,且在即将遭遇时有发散的趋势,不利于弹体的稳定及精确拦截。
图5所示为导弹的舵偏角变化曲线。末制导初始段舵偏角变化较快、幅值较大,随着视线角趋于稳定,舵偏角变化随之趋缓,整个过程舵偏角均未超出舵机物理限制;在导弹即将遭遇目标时,采用一体化设计方法得到的舵偏角几乎不再变化,而采用传统方法设计的导弹舵偏角需要迅速变化,虽然变化速度及幅值未超出舵机物理限制,但由于导弹存在制导盲区,进入盲区后舵机锁定,实际应用上舵机根本无法执行,因此必然会带来较大脱靶量。
5 结论
本文对制导控制一体化设计方法进行了深入研究。首先推导出俯仰通道的制导控制一体化数学模型,并合理转化为一个级联系统。然后引入动态面方法并结合干扰观测器技术,提出了一种基于非线性干扰观测器的积分动态面一体化制导控制系统设计方法,在每一个子系统设计时引入误差的积分项以消除稳态误差,提高了子系统的跟踪精度,并进行系统稳定性分析。仿真结果表明,相对于传统制导、控制分开设计方法,本文所提出的一体化控制算法在视线角速度收敛时间、攻角稳定性、舵机偏转幅度、拦截精度等方面全部占优。
参考文献
[1]严晗.鲁棒非线性导引与控制律一体化设计研究[D].合肥:中国科学技术大学博士学位论文,2013.
[2]李运迁.大气层内拦截弹制导控制及一体化研究[D].哈尔滨:哈尔滨工业大学博士学位论文,2011.
[3]Yamasaki Takeshi,Balakrishnan S.N.,Takano Hiroyuki. Separate-Channel Integrated Guidance and Autopilot for Automatic Path-Following[J].Journal of Guidance Control and Dynamics.2013,36(1):25-34.
[4]Wang Xianghua,Wang Jinzhi.Partial Integrated Missile-Guidance and Control with Finite Time Convergence[J]. Journal of Guidance,Control,and Dynamics.2013,36 (5):1399-1409.
[5]侯明哲.寻的导弹导引与控制一体化设计[D].哈尔滨:哈尔滨工业大学博士学位论文,2011.
[6]Levy Maital,Shima Tal,Gutman Shaul.Integrated Single vs.Two loops Autopilot-Guidance Design for Dual-Controlled Missiles[C].10th IEEE International Conference on Control and Automation,Hangzhou,China, 2013.
[7]Yamasaki Takeshi,Balakrishnan S.N,Takano Hiroyuki. Separate-Channel Integrated Guidance and Autopilot for Automatic Path-Following[J].Journal of Guidance Control and Dynamics,2013,36(1):25-34.
[8]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000.
[9]张保群,宋申民.基于自适应滑模控制的导弹制导与控制一体化反演设计[J].弹箭与制导学报,2009,29 (5):31-35.
[10] 甄红涛,齐晓慧,夏明旗.四旋翼无人机块控反步姿态控制器设计[J].电光与控制,2013,20(10):87-91.
[11]Yang Jun,Li Shihua,Sun Changyin.Nonlinear-Disturbance-Observer-Based Robust Flight Control for Airbreathing Hypersonic Vehicles[J]IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1263-1275.
中图分类号:TJ765.2
文献标志码:A
文章编号:2095-8110(2014)03-0025-06
收稿日期:2014–03–20;
修订日期:2014–06–10。
作者简介:马文桥(1986–),男,博士研究生,主要从事制导、控制方面的研究。E-mail:flyhorsema@163.com
Integrated Guidance and Control Design Method for Missile Based on Dynamic Surface
MAWen-qiao1,HE Chen-di1,SHI Zhen1,HUANG Han2,MAGuo-qiang3
(1.Automation College,Harbin Engineering University,Harbin,150001,China;2.Beijing Electro-Mechanical Engineering Institute,Beijing 100074,China;3.Harbin Jiancheng Group CO.,LTD,Harbin 150030,China)
Abstract:In order to avoid the defects of traditional design method,which design guidance and control system separately,the two systems are considered together,an integrated guidance and control design method is proposed.Firstly,mathematical model of integrated guidance and control is derived in pitch channel,and converted to cascade form;then an integrated guidance and control design method based on dynamic surface and nonlinear disturbance observer is proposed,integral term is introduced when designing each subsystem to eliminate the steady state error and improve the tracking accuracy.And system stability is analyzed by using Lyapunov function;finally,simulation results verified the effectiveness of the control algorithm.
