基于ESO的再入飞行器姿态控制

詹 韬，梅金平，郑 旭

（北京控制与电子技术研究所，北京100038）

基于ESO的再入飞行器姿态控制

詹 韬，梅金平，郑 旭

（北京控制与电子技术研究所，北京100038）

摘 要：针对飞行器再入姿态控制系统受到较大干扰力矩时，采用目前工程上常用的“前馈＋PID”控制方法难以获得理想控制精度的问题，提出了采用自抗扰控制技术进行再入姿态控制的方法。首先利用扩张状态观测器对前馈项没有完全补偿的剩余飞行器角加速度进行估计并加以补偿，使得作用在飞行器上的力矩接近于平衡状态，并采用PD控制器进行误差反馈控制，给出了飞行器再入姿态自抗扰控制律，并在频率域分析的基础上给出了控制参数设计原则。仿真结果表明采用本方法能够有效地克服干扰力矩，从而明显地提高再入飞行器姿态动态跟踪精度。

关键词：再入飞行器；姿态控制；自抗扰控制；扩张状态观测器

0　引言

飞行器再入姿态控制问题是典型的高不确定性、严重非线性、强耦合、快时变的多变量系统控制问题，一直以来是控制领域的难点之一。针对该问题，目前工程上应用较为成熟的控制方法有“前馈+PID”控制、滑模变结构控制、基于极点配置的状态反馈控制等。这些方法均属于基于误差反馈的控制方法，当系统受到大干扰力矩且干扰力矩变化较快时，难以获得很好的控制品质，且控制参数设计往往较为复杂。

自抗扰控制技术是韩京清先生于20世纪80年代末期创建的一种估计补偿不确定因素的控制技术。自抗扰控制器最突出的特征就是把作用于被控对象的所有不确定因素——建模误差和外加干扰——都归结为“总的未知扰动”，并利用对象的输入输出数据对它进行估计并给予补偿[1]，从而使控制系统获得更好的闭环动态性能。近年来，自抗扰控制技术在巡航飞行器[2]、航空飞行器大包络线飞行控制[3]、无人机飞行控制[4]等领域都得到了成功的应用。

本文提出采用自抗扰控制思想设计飞行器再入姿态控制系统三通道控制器——每个通道均把各自受到的耦合干扰、气动系数偏差以及总体结构偏差等所有不确定因素当作“总的未知扰动”，通过自抗扰控制技术中的扩张状态观测器（ESO）进行估计并加以补偿，再采用PD控制器进行误差反馈控制，从而提高再入姿态控制系统的抗干扰能力。

1“前馈+PID”控制方法遇到的问题及自抗扰控制器设计思想

对于飞行器再入姿态控制问题，目前工程上常用的控制方法是对俯仰、偏航、滚动通道分别设计“前馈+PID”控制器独立进行稳定控制。“前馈+PID”控制器的设计思想是首先利用前馈和积分控制的作用对气动耦合干扰力矩、气动恢复力矩和由气动系数偏差、风、弹体结构偏差、气动烧蚀等不确定因素引起的干扰力矩进行补偿，使飞行器基本处于力矩平衡状态，再利用PD反馈控制作用，使飞行器在平衡点附近具有足够稳定性的同时，平稳地跟踪指令姿态角。对于采用该控制方法的姿态控制系统，当气动干扰力矩和指令姿态角变化较缓慢时，具有较好的控制效果。但是，当以上条件不满足时，由于积分控制作用延迟较大，无法及时补偿快变的干扰，将使系统偏离平衡状态，使姿态动态跟踪品质变差（见图1），并且当系统状态偏离平衡状态较多时，平衡点附近基于小扰动线性化模型设计的反馈控制器将有可能失效，导致系统发散。因此，如何提高对干扰的动态补偿精度，是进一步提高飞行器再入姿态控制系统动态性能的关键。

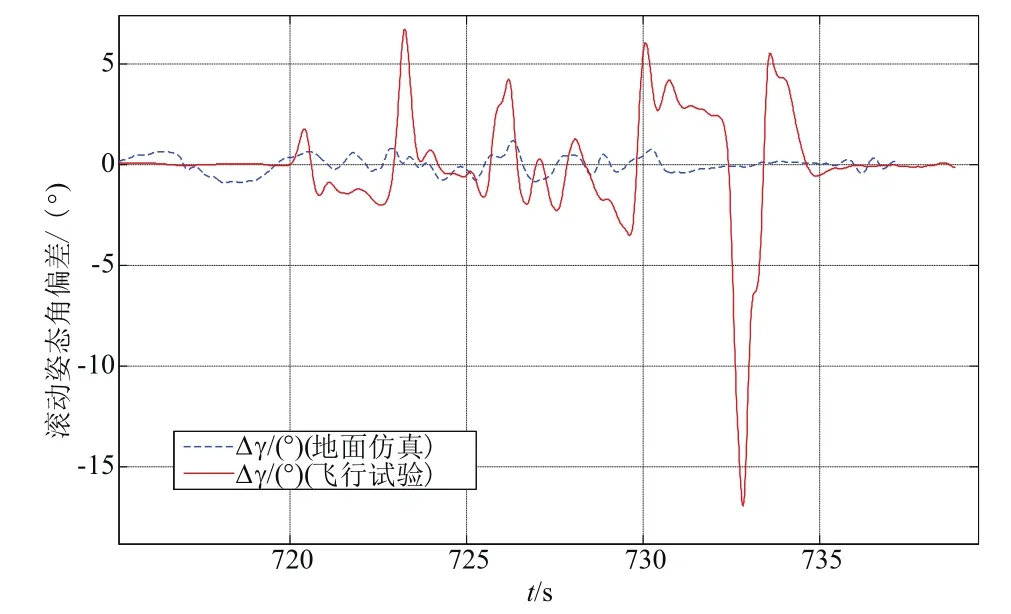
图1　滚动姿态角偏差Fig.1 Error of roll attitude angle

要提高对干扰的补偿精度，一方面可提高前馈补偿精度，但总体设计提供的气动数据与实际飞行的气动数据不可能一致，根据地面数据得到的配平关系存在偏差，因此提高前馈精度对提高抗干扰能力作用有限。那么，另一方面，能否通过提高积分项对干扰的动态补偿精度来获得理想的控制效果呢？针对该问题，自抗扰控制技术提供了很好的解决思路：首先利用自抗扰控制技术中的扩张状态观测器（ESO）对前馈项没有补偿掉的弹体角加速度进行估计，再将估计结果折算成舵摆角对这部分角加速度进行补偿，从而提高对干扰的补偿精度。

2　扩张状态观测器建立

状态观测器原理是利用原系统的输入和输出信息估计系统内部未知状态。而扩张状态观测器就是把被观测系统中的所有不确定的角加速度的总和扩张为新的状态量，并连同其它状态量一起进行估计的观测器。因此，设计扩张状态观测器需要首先确定被观测系统动力学模型中哪些是已知的部分，而哪些是需要被扩张为新状态加以估计的未知部分。

2.1扩张状态量的确定

确定扩张状态量实际上就是要确定系统运动微分方程的右端角加速度中哪些是已知部分，哪些是需要被估计的未知部分。由于文献[1]提出当数字控制系统采样周期T给定时，扩张状态观测器能够较好地估计的最大角加速度约为1/4T(rad/s2)，而且在该范围内角加速度越小，被估计的精度越高。因此，确定扩张状态量的指导原则是：从系统总的角加速度中提取出主要分量，将其作为已知部分，而将剩余部分当作未知分量，利用观测器对这小部分未知分量进行估计，从而确保在采样周期T给定的条件下获得较好的估计精度。根据该原则，对于本文研究的飞行器姿态控制系统，其扩张状态量确定过程如下。

首先写出再入姿态运动微分方程（以滚动通道为例）：

式中： ωxb是角速度； Jxb是转动惯量； MxbQ、Mxbq、MxbI、MxbB分别是空气动力矩、阻尼力矩、惯性力矩和结构干扰力矩。对于在大气层内飞行的飞行器来说，其所受外力矩主要是空气动力矩MxbQ，其余力矩与之相比很小，且具有不确定性，因此首先将它们当作是未知扰动的一部分。而对于主要的空气动力矩MxbQ，将对其进一步分解，从中分离出已知部分和未知部分。

在考虑气动力矩系数偏差的情况下，空气动力矩MxbQ的表达式如下：

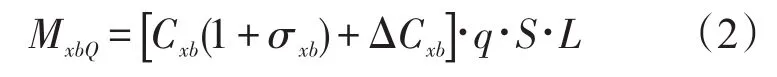
式中：Cxb是气动力矩系数；σxb和ΔCxb分别是气动力矩系数比例偏差和常值偏差；q是动压；S、L分别是飞行器参考面积和参考长度。通常气动力矩系数Cxb可分解成如下形式：

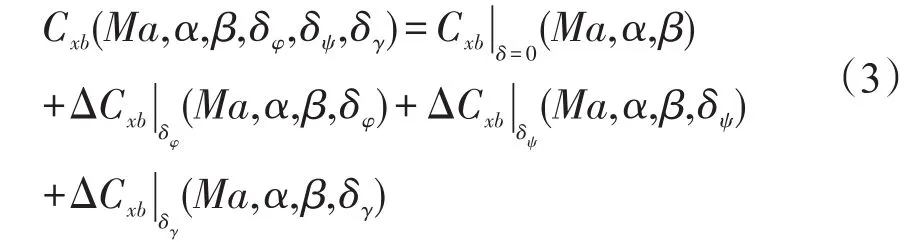
式中：Cxb|δ=0是零舵偏角条件下的气动力矩系数；分别是俯仰、偏航和滚动舵偏角产生的气动力矩系数增量。在不考虑PD控制的情况下，舵偏角δγ由δγ0和Δδγ两部分组成，即δγ=δγ0+Δδγ，那么式（3）可写为如下形式：

式中：Cxb(Ma,α,β,δφ,δψ,δγ0)是当舵偏角取近似配平舵偏角δγ0时的气动力矩系数，当δγ0等于理论配平舵偏角时，； ηxb为的近似值；Rxb2是以(ηxb+Δηxb)Δδγ替代Cxb(Ma,α,β,δφ,δψ,δγ)-Cxb(Ma,α,β,δφ,δψ,δγ0)的线性近似误差。

将式（4）代入式（3）并经过整理可得空气动力矩MxbQ的如下表达式：

式中：

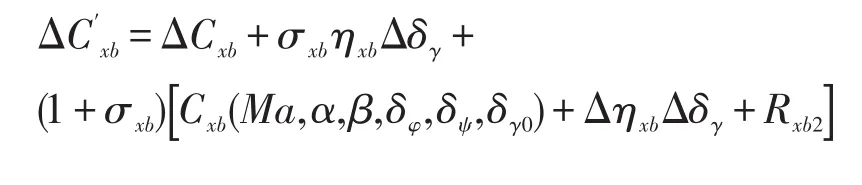
在式（5）中，ηxbΔδγqSL是空气舵产生的气动控制力矩的主要成分，因此将其作为已知模型，而将ΔC′xbqSL作为未知空气动力矩，它与Mxbq、MxbI和MxbB一起构成总的未知干扰ΔMxb，从而将动力学方程（1）写成如下形式：

式中：bxbΔδγ=-(ηxbqSL/Jxb)Δδγ是角加速度的主要分量，是已知部分模型，而Δxb=ΔMxb/Jxb是总的未知干扰加速度，它即包含类似ΔCxbqSL/Jxb、σxbηxbqSLΔδγ/Jxb、MxbB这样的外加干扰加速度，又包含诸如这样的，由于建模不准确而造成的误差加速度。利用自抗扰控制的设计思想，把总的干扰角加速度Δω.xb作为被扩张的状态量，利用扩张状态观测器对它进行估计。

2.2扩张状态观测器方程建立

状态观测器的输入量是被观测系统的输入量和输出量，输入量的选择将决定着观测品质。由于通常姿态角速度量测信号中存在噪声，而扩张状态观测器带宽较宽并且对噪声有放大作用，如果以角速度作为扩张状态观测器的输入信号，那么势必将噪声放大后引入系统，从而影响系统性能。而角度信号是角速度的积分，经过积分，噪声将大大减小，因此，扩张状态观测器的输入信号采用角度信号θxb。

下面以滚动通道为例，建立其扩张状态观测器方程。设系统的状态变量为：x1x=θxb、x2x=ωxb、x3x=Δ.xb，其中 x3x=Δxb是被扩张的状态。根据系统动力学方程（6）可写出其对应的状态方程：

根据式（7）可建立飞行器姿态控制系统（以滚动通道为例）的扩张状态观测器方程：

式中： z1x是θxb的观测量、 z2x是 ωxb的观测量、z3x是干扰角加速度 Δω.xb的估计量； β1x、 β2x、β3x是扩张状态观测器的误差反馈增益。通过合理选择参数 β1x、 β2x、 β3x可使 z3x准确地估计干扰角加速度Δω.xb。

扩张状态观测器结构框图如图2所示。由图可知，扩张状态观测器的输入量分别是系统的输入量Δδγ和输出量θxb，它利用系统的输入和输出信息对系统内部的未知干扰Δω.xb进行估计。对观测器方程（7）进行拉普拉斯变换并消元整理可得观测器传递函数：

由式（9）可知，所谓干扰角加速度Δω.xb的估计量z3x，本质上就是将干扰角加速度Δω.xb经过一个低通滤波器滤波后得到的结果。

图2　ESO结构图Fig.2 Structure of ESO

3　自抗扰控制律设计

如上文所述，在获得干扰角加速度Δω.xb的估计值z3x后，可通过控制量Δδγ加以补偿，使补偿后的角加速度接近于零（即力矩平衡状态）。由于z3x≈Δ.xb，将其代入式(6)可得：

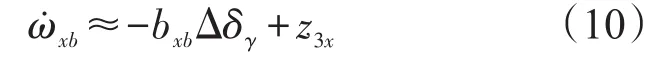
由式（10）可知当Δδγ=z3x/bxb时， ω.xb≈0，因此当舵偏角δγ等于δγ0+z3x/bxb时，当前通道将处于近似力矩平衡状态，δγ0+z3x/bxb即为近似配平舵偏角。

在力矩平衡的基础上，要想使得闭环系统以期望的动态特性跟踪指令姿态角，还需要设计合适的误差反馈控制器。本文采用经典的PD控制器进行误差反馈控制，因此得到如下形式的控制律：

式中：Δγ、Δωxb分别为姿态角偏差和角速度偏差；、分别为比例和微分控制增益。

采用自抗扰控制律进行控制时的系统原理框图见图3（以滚动通道为例）。

图3　自抗扰控制原理框图Fig.3 Structure of control system based on ESO

4　自抗扰控制器频率域分析及参数确定

4.1自抗扰控制器频率特性分析

本节以俯仰通道为例对自抗扰控制器和传统的“前馈+PID”控制器频率特性进行对比分析。

在控制方程（11）中用上一控制周期的舵指令作为当前控制周期舵偏角的估计值，即在控制方程中取δφ=δφC(t-T)（T为控制周期），并作近似处理：，可根据式（11）得到小扰动条件下的自抗扰控制器方程为：

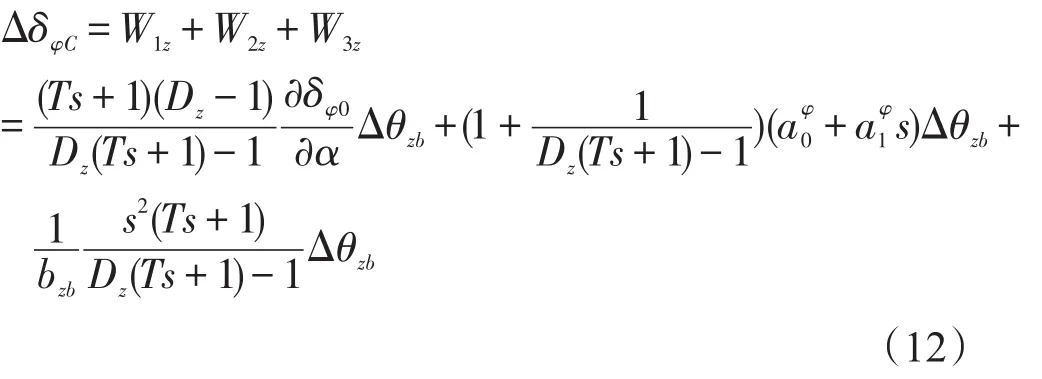
式中：Δθzb为姿态角小扰动量；为前馈项；为 PID控制项；为加速度反馈项。

采用自抗扰控制时，小扰动条件下的控制系统框图如图4所示。

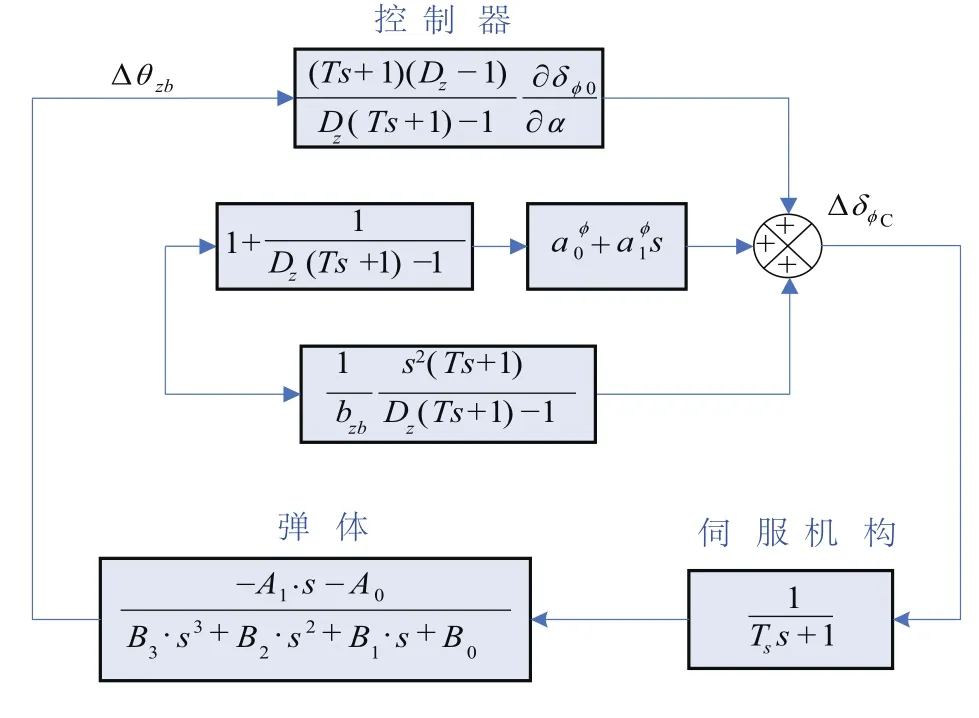
图4　小扰动条件下控制系统框图Fig.4 Schematic diagram of control system based on small perturbation condition

从前文可知，自抗扰控制器与传统的“前馈+ PID”控制器相比增加了角加速度反馈项，体现在方程（12）中就是增加了W3x，增加该项可等效为在原控制器结构上串联一个环节G。

前馈项W1x对控制器频率特性影响很小，将其忽略后可得：

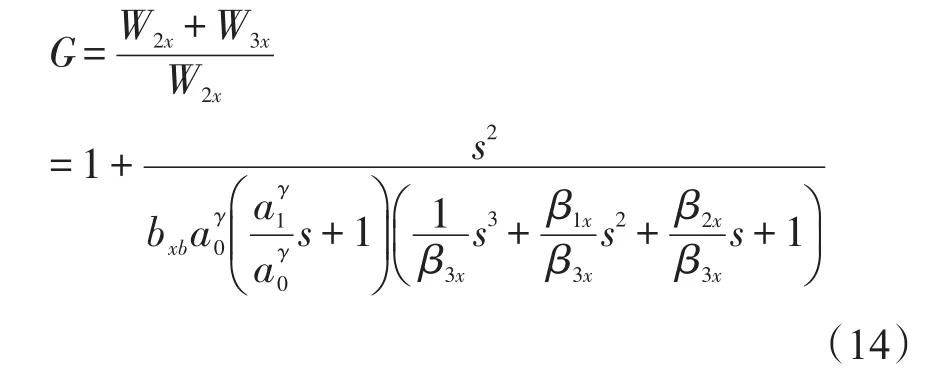
由图5和图6可知，加入角加速度反馈近似等效于在开环系统中串入一个“反向陷波器”。若β3x不变，增大 β1x、 β2x可以降低“反向陷波器”的幅频特性，有利于提高系统幅值裕度；若 β1x、β2x不变，减小 β3x则可以减小“反向陷波器”的相位滞后，有利于提高系统的相位裕度。因此，增大β1x、 β2x同时减小 β3x有利于提高系统稳定性。

图5　G的幅频特性Fig.5 Amplitude-frequency characteristic of G

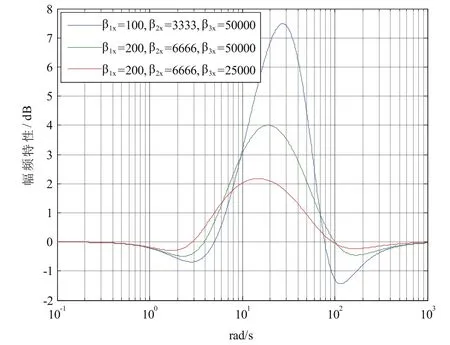
图6　G的相频特性Fig.6 Phase-frequency characteristic of G

4.2观测器参数和PD控制增益的确定原则

文献[1]通过数值仿真得到了以下结论：当控制周期T给定时，扩张状态观测器的参数 β1x、β2x、β3x如果按照下面的经验公式确定，那么观测器就能较好地估计出角加速度不超过M=范围的系统的状态和角加速度。

根据该结论，当控制周期T为0.01s时，扩张状态观测器参数取为：β1x=100、 β2x=3333、β3x=50000，那么观测器就能较好地估计出不超过25rad/s2的干扰角加速度。那么，在设计参数时可首先按照经验公式（15）～（17）确定一组初始的观测器参数，确保系统有较好的抗干扰能力，再利用频率域综合设计方法对PD控制增益进行设计，并对观测器参数进行适当调整，确保系统具有足够稳定性。

5　试验研究

以某飞行器再入飞行段为例，该飞行器为轴对称飞行器，采用“十”字空气舵进行姿态控制，分别使用本文提出的自抗扰控制方法和传统的“前馈+PID”控制方法进行控制，在考虑各种典型干扰的条件下进行仿真试验。仿真系统结构框图见图7。

图7　仿真系统结构框图Fig.7 Structure diagram of simulation system

试验结果表明：在各种典型干扰条件下，扩张状态观测器均能够很好地估计干扰角加速度，从而能够准确地对其进行补偿，使得采用自抗扰控制器后的姿态动态跟踪品质相比传统的“前馈+ PID”控制方法有明显提高。

图8～图11是某典型干扰条件下仿真曲线。仿真时分别采用自抗扰控制器和“前馈+PID”控制器进行仿真。从对比结果可知，在干扰条件下，采用自抗扰控制器的控制偏差远小于“前馈+ PID”控制器的控制偏差。该结果表明自抗扰控制器能够有效地克服干扰力矩，从而明显地提高飞行器的姿态动态跟踪精度。

图8　俯仰姿态角偏差Fig.8 Error of pitch attitude angle

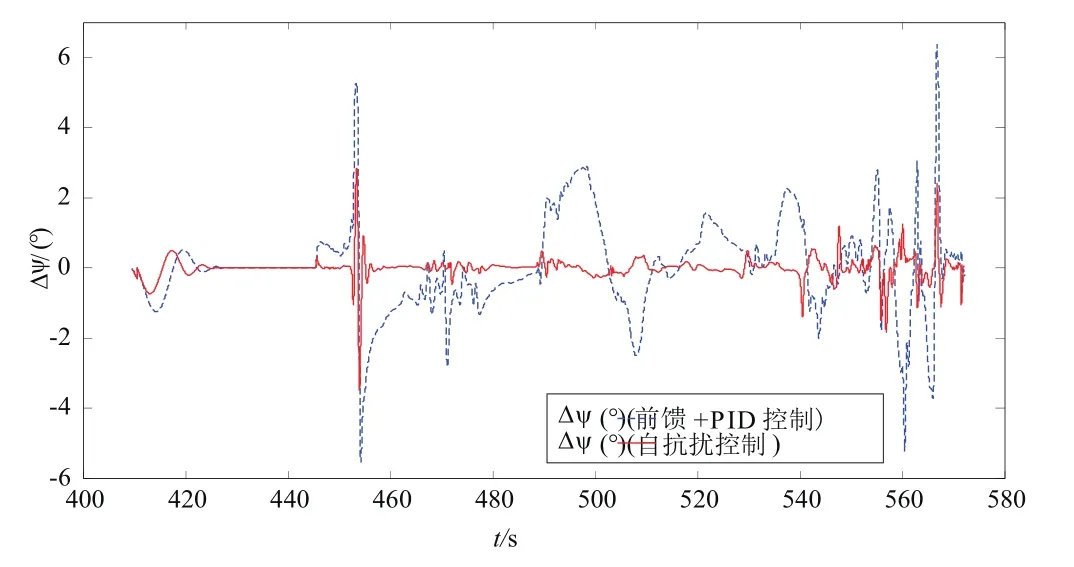
图9　偏航姿态角偏差Fig.9 Error of yaw attitude angle

图10　滚动姿态角偏差Fig.10 Error of roll attitude angle

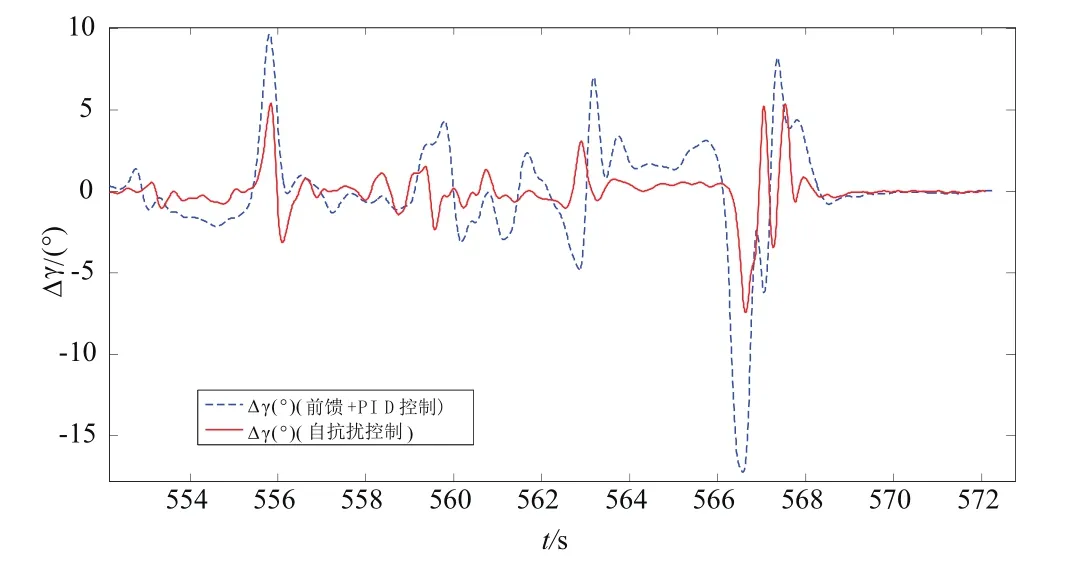
图11　滚动姿态角偏差（局部放大）Fig.11 Error of roll attitude angle（local amplification diagram）

6　结论

自抗扰控制技术的应用为更好地解决飞行控制系统在干扰条件下的控制问题提供了一种新的思路。它直接针对非线性模型，将非线性模型中不确定的部分连同外加干扰一起当作总的干扰，采用扩张状态观测器进行估计并加以补偿，使补偿后的飞行器接近力矩平衡状态，再采用误差反馈控制器（如PD控制器）进行反馈控制，从而获得理想的闭环动态性能。从设计过程上看，设计时无需过多地考虑系统中非线性干扰因素，设计过程简单。从控制效果上看，与传统的“前馈+ PID”控制律相比，采用自抗扰控制器能够获得更好的控制精度。应用该方法在解决飞行器大攻角飞行时的强耦合问题、远距离再入滑翔飞行器烧蚀引起的气动干扰问题，以及制导指令快速变化等再入控制问题上有着较大的优势。

参考文献

[1]韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].国防工业出版社，2009.

[2]孙明玮，焦纲领，杨瑞光，陈增强.自抗扰控制在飞行器控制与制导上的应用与分析[C].第29届中国控制会议论文集，2010:6167-6172.

[3]熊治国，孙秀霞，胡孟权.自抗扰控制器在大包线飞行控制中的应用[C].第24届中国控制会议，2005:1481～1484.

[4]胡海燕，等.飞行控制系统的自抗扰控制设计[C].尖兵之翼——2006中国无人机大会论文集，2006.

中图分类号：TP13

文献标志码：A

文章编号：2095-8110（2014）03-0018-07

收稿日期：2014–03–03；

修订日期：2014–09–24。

作者简介：詹韬（1983–），男，硕士，工程师，主要从事飞行器姿态控制方面的研究。E-mail:james_1064@126.com

Attitude Control Method of Re-entry Flight Vehicle Based on ESO

ZHAN Tao,MEI Jin-ping,ZHENG Xu
（Beijing Control and Electronic Technology Research Institute，Beijing 100038，China）

Abstract：Due to the great disturbance on the attitude control system of re-entry vehicle,the current widely used control method in engineering,which is called as“PID with Feedforward Control”,is difficult to obtain satisfactory system performance.In this paper,the idea of using Active Disturbance Rejection Control（ADRC）technology to design attitude controller of re-entry vehicle is proposed.Firstly,the residual attitude angular acceleration without compensation by feedforward controller is estimated and compensated by making full use of ESO,this would make the flight moments close to the balance states.Secondly,PD controller is introduced for error-feedback control.Thirdly,some principles for designing control parameters based on frequency domain analysis are given.Finally,Simulation results show that ADRC can effectively overcome the attitude disturbance generated by the disturbing torque,thereby significantly improve the dynamic tracking accuracy of aircraft attitude.

Key words:Re-entry flight vehicle;Attitude control;ADRC;ESO