基于μ综合方法的自动驾驶仪设计

王建琦，杨育荣，郑鲲鹏

（中国空空导弹研究院，河南洛阳471000）

基于μ综合方法的自动驾驶仪设计

王建琦，杨育荣，郑鲲鹏

（中国空空导弹研究院，河南洛阳471000）

摘 要：对于具有不确定性的控制系统，如何保证控制系统的设计能够具有鲁棒性，同时又达到最优的控制性能， μ综合方法以完备的结构奇异值理论为基础，给出了这一问题的最优解。导弹受控飞行于稠密大气层时，其自动驾驶仪正是这样一种要面对多种不确定性因素的控制系统，为使导弹控制在这种情况下达到鲁棒最优，将 μ综合方法用于导弹自动驾驶仪设计，并对设计结果进行了仿真验证，结果分析表明采用该方法对于导弹气动不确定性具有更好的鲁棒效果。

关键词：鲁棒控制； μ综合；D-K迭代算法；自动驾驶仪

0　引言

反馈控制系统的原始动机是提供满意的性能给存在模型误差、不确定性变化的系统。反馈只有在系统特征中的不确定性使其性能达不到要求时才需要引入。如果给定了一个具有不确定性描述的模型，并认为该模型恰当表达了对象的基本特征，控制器设计的下一步便是确定何种结构可以达到期望的性能，预滤波输入信号（或开环控制）能够改变模型集合的动态响应，但不能减小不确定性的影响，若不确定性太大以至于达不到期望的控制性能，就需要反馈结构。然而仅有反馈结构并不能保证减小不确定性的影响，要达到利用反馈减小不确定性影响的目的还存在许多障碍，因为对于表示物理系统的不确定性的任何一个合理模型集合，在足够高的频率处会变大且相位完全未知，因此必须在这些频率上尽可能的减小闭环增益，以避免高频系统的动态不稳定。

更糟的是，反馈系统实际上在不确定性很大的频段上增大了系统的不确定性和灵敏度。也就是说，由于对建立合理的物理系统模型集合难以全面描述的限制，不能利用反馈（或任何其它控制结构）使闭环模型集合成为开环模型集合的一个有理子集，而能够达到的是：通过利用反馈显著降低对某些重要信号的不确定性，同时对其它信号不确定性的增加很小[1]。因此，反馈设计的核心是围绕如何降低不确定性的综合影响进行折中。但这无疑使得控制系统性能的发挥打了折扣，因为通常情况下折中的考虑会导致设计的保守性，如何针对不确定性，使得控制系统设计既能够抵抗这些不确定性（即具有鲁棒性），又能够达到较优的控制性能，成为这种情况下反馈系统的设计核心。而传统的古典控制由于具有上述先天不足，因而使得基于现代控制理论的鲁棒控制自20世纪90年代以来迅速发展，并应用于工程设计。

导弹受控飞行于稠密大气层中，由于控制系统建模的复杂性，其自动驾驶仪设计不得不面临多种不确定性因素。诸如气动建模不准、气动本身的不确定性、风干扰、传感器建模误差等（其中气动特性不确定性影响最为重要）[2]。传统设计方法通过提高稳定裕度的保守设计来降低不确定性的影响，但这也使得自动驾驶仪的性能打了折扣。鲁棒控制对此给出了较好的解决办法[3]，H∞控制虽然是基于现代控制理论的鲁棒设计，但其所固有的保守性设计仍然以鲁棒为主，而μ综合方法以完备的结构奇异值理论为基础，能够达到控制系统设计鲁棒最优，这正是自动驾驶仪的设计所要达到的目标，因此本文采用μ综合方法开展了导弹自动驾驶仪设计，首先介绍了μ综合方法D-K迭代的控制算法，然后基于此对导弹纵向通道驾驶仪的数学模型进行了相应的转换和描述，将传统的小扰动线性化的动力学模型转换为状态空间的形式，通过利用matlab的鲁棒控制工具箱进行μ综合控制器设计，最后对设计的控制器进行了仿真验证和分析。

1　μ综合方法概述

μ综合方法以结构奇异值理论为基础，不但能够有效地、无保守地判断最坏情况下摄动的影响，且当存在不同表达形式的结构化不确定性时，能够分析控制系统的鲁棒稳定性和鲁棒性能[4]。与其他鲁棒控制方法相比，更具有以下优点：

1）结构化不确定性可以完全直接引入到控制器设计中，无需将其转化为一类更大范围的不确定性，从而导致了不必要的保守性；

2） μ方法还可以对鲁棒性能进行分析与综合，不像H∞优化方法只能进行鲁棒稳定性的分析和设计控制器。

目前， μ综合的有效近似方法为“D-K迭代”。假设K是状态或/和输出反馈矩阵，M为广义标称对象矩阵，Δ为结构不确定性矩阵，且满足(Δ(jω))＜1,∀ω∈R，根据小 μ定理可知该系统鲁棒稳定的充要条件是：

1）反馈控制器K能够使对象闭环稳定，构成稳定的标称系统，即K可以镇定M；

2） μΔ(M(K))＜1,∀ω∈R。

其中M(K)可表示为M和K的下线性分式变换形式Fl(M,K)，并根据μ的基本性质定理，则上述充要条件可转化为：

1）Fl(M,K)∈RH∞；

μ综合设计的目的就是寻找正则控制器K，使上述条件成立，其中标度矩阵D可以选择为稳定的最小相位阵，并满足

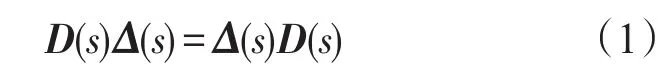
即可。

根据转化后的条件（2），通过反复求解K和D，最终得到满意的μ值。考虑到性能最优问题，μ综合问题由条件（2）进一步转化为：

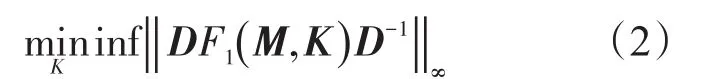
若D固定，则为：

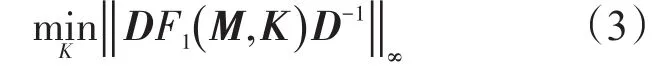
此时为标准H∞控制问题；若K固定，则为：

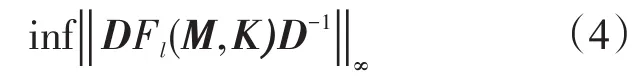
此时为一个关于D的凸优化问题。

由此可知最优化 μ综合问题的D-K迭代的基本思想是：先固定D，获得最小化的K；再固定K，获得最小化的D；再固定D，求最小化的K，以此类推，最终获得最优的D和K。D-K迭代算法描述如下：

1）选择初始标度矩阵D(s)；

2）固定D(s)，求解式（3）的H∞控制问题，得到控制器K(s)；

3）固定K(s)，求解式（4）的凸优化问题,得到标度矩阵ˉ(s)；

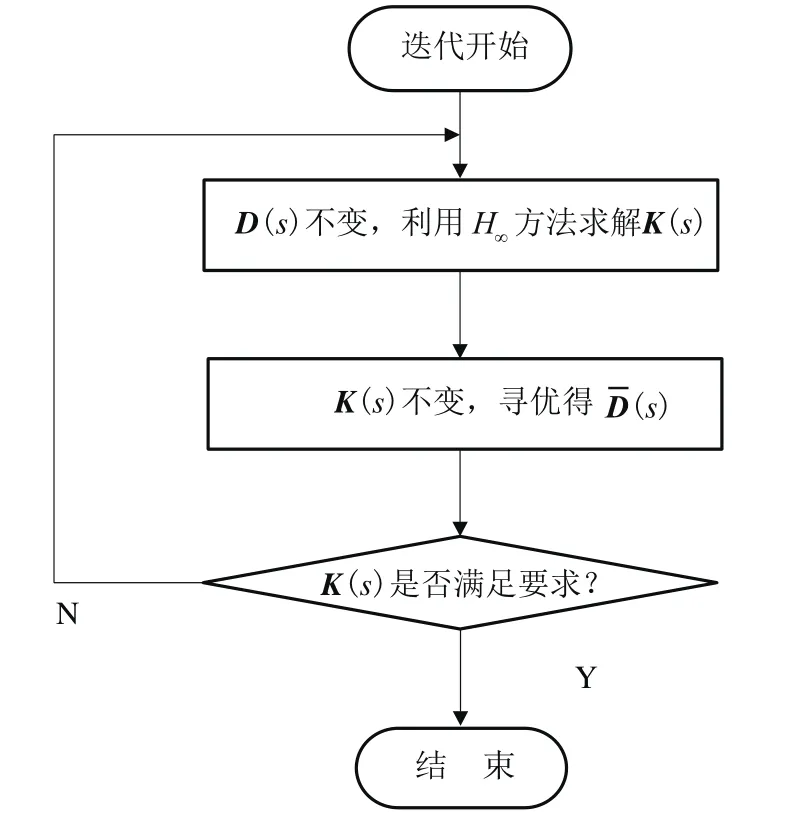
图1　D-K迭代算法流程Fig.1 D-K iteration algorithm program

虽然D-K迭代不能保证获得全局最优解，但通常情况下迭代所得的控制器是十分有效的，这也是D-K迭代有待提高改进之处。

2　导弹的μ综合控制设计

导弹纵向自动驾驶仪设计时通常采用小扰动线性化的方法，从而获得各动力学变量的传递函数，进而通过对传递函数进行参数设计。由于本文采用鲁棒最优控制方法，因此将传统的小扰动线性化的动力学模型转换为状态空间的形式，以便于进行μ综合的设计和分析。

导弹的纵向运动可以用小扰动方程来近似描述。我们把导弹纵向运动的传递函数用状态方程的形式描述如下[5]：

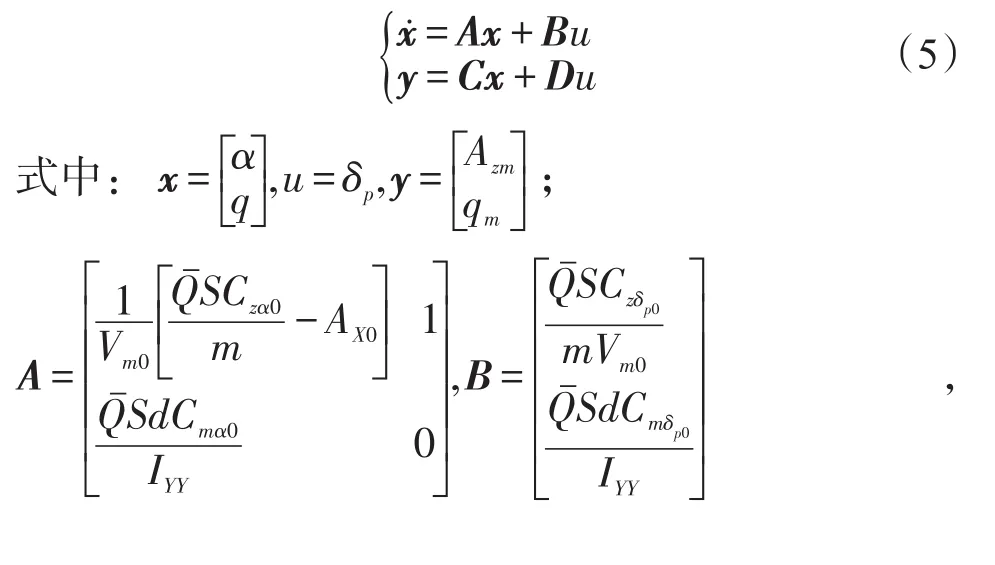
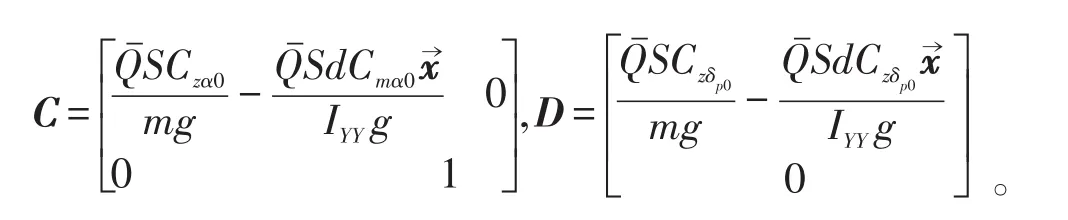
主要变量的含义如表1所示。

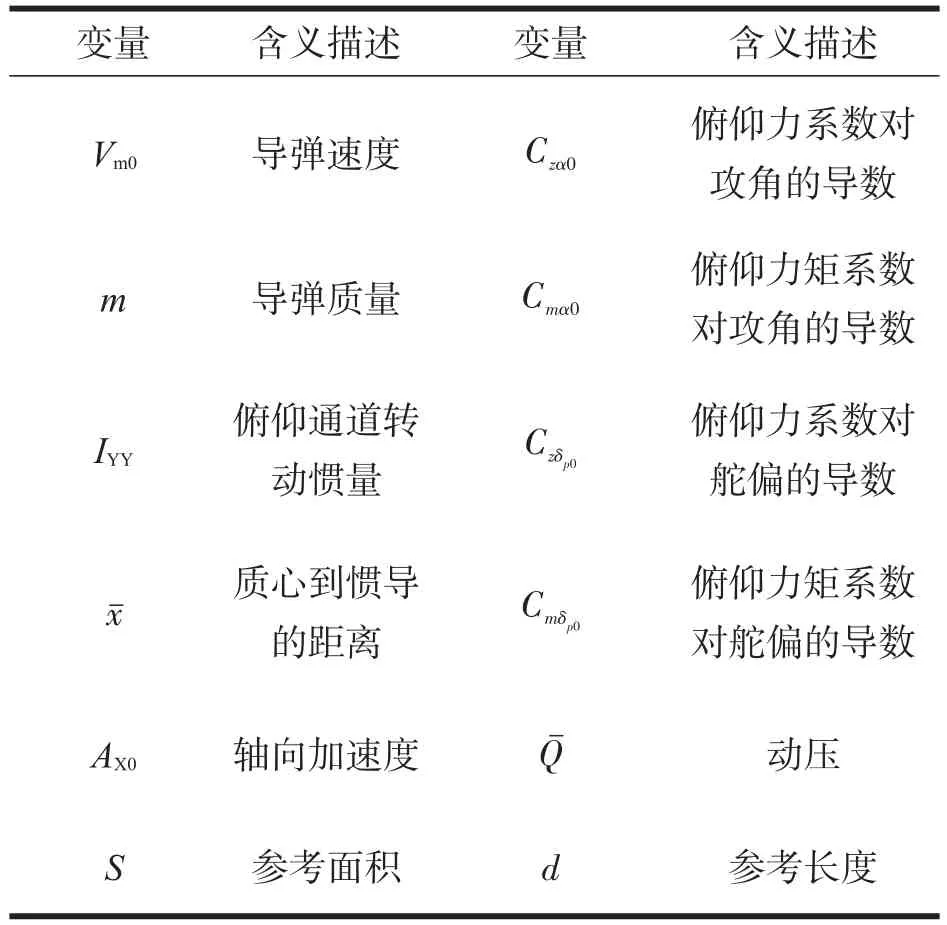
表1　主要变量的含义Tab.1 The meaning of main variables

基于 μ综合的导弹控制系统框图如图2所示,其目的是设计μ综合控制器在各种噪声W以及不确定性的影响下，使导弹实际过载能够正确的跟踪过载指令。

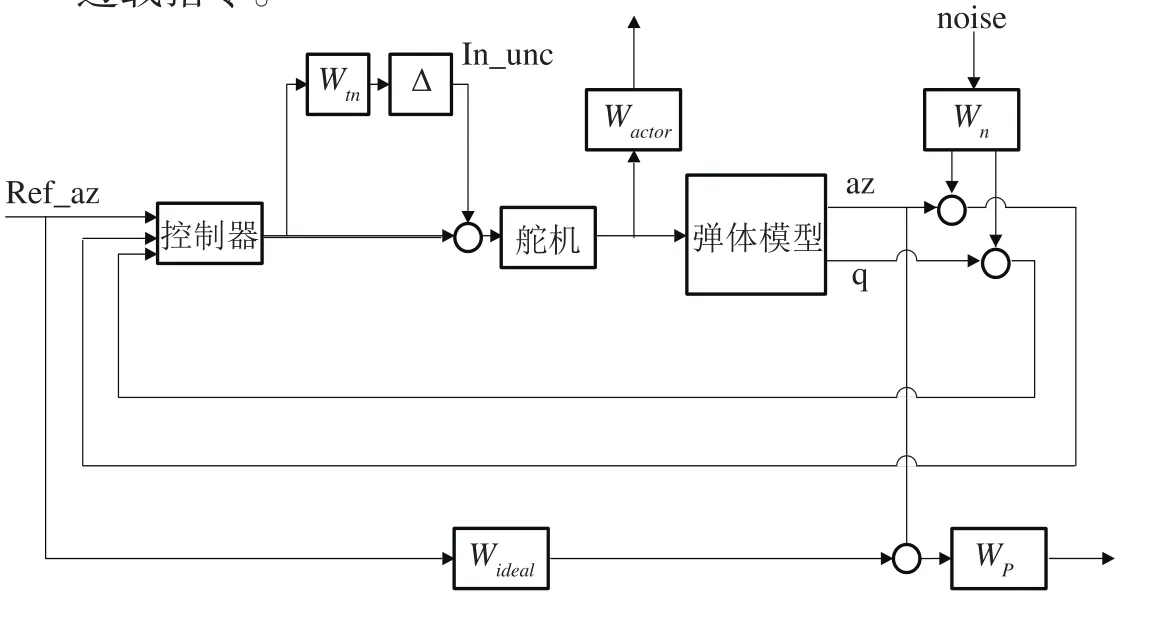
图2　μ综合自动驾驶仪结构Fig.2 Structure ofμsynthesis autopilot

选取特征点高度5km、马赫数0.9、“X”飞行状态进行控制器的设计。在标称系统设计完备的基础上，利用matlab的鲁棒控制工具箱进行μ综合控制器设计，根据图2建立好系统模型并设定了各项参数后，可自动进行D-K迭代过程，每一步都可由设计人员针对具体情况进行人工干预，每一步设计的中间结果也可以清楚地显示出来，设计界面和参数如下面图3、图4所示。

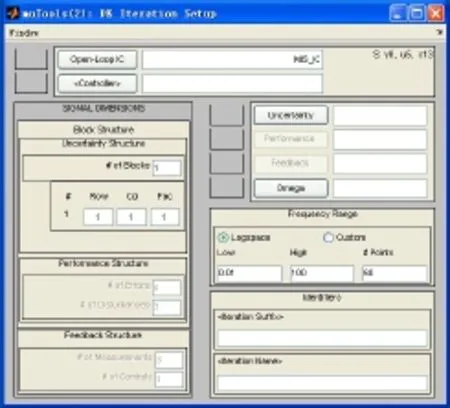
图3　μ综合控制器设计平台界面1Fig.3 Design platform 1 ofμsynthesis controller

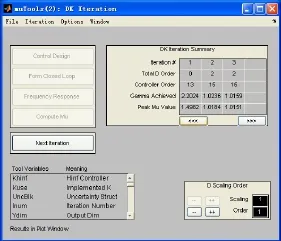
图4　μ综合控制器设计平台界面2Fig.4 Design platform 2 ofμsynthesis controller

将D-K迭代最终获得的控制器矩阵带入图2所示的控制器结构，并进行仿真，时域响应结果如图5、图6所示。

图5　纵向线加速度阶跃响应Fig.5 Step response of acceleration

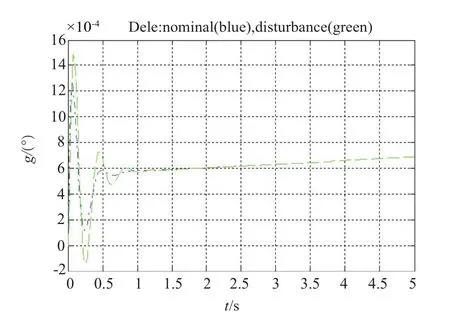
图6　纵向舵输出Fig.6 Output of the pitch fin

图5中加速度信号给出了理想情况下（期望达到的响应特性）、标称情况下（考虑到模型不确定性Δ）、拉偏（气动力/力矩拉偏,均为20%【6】）情况下的阶跃响应。可以看出，所设计的控制器能够使导弹控制系统基本达到期望的响应特性，并且在气动力/力矩不确定的情况下，具有较强的鲁棒性。

3　针对不确定性的μ分析

μ综合控制器与传统控制器性能比较的方法是采用μ理论中的鲁棒分析方法对传统控制器进行分析，并给出与 μ综合控制器相对应的鲁棒稳定性和鲁棒性能指标，包括最大结构奇异值、标称性能与最坏扰动情形的比较。传统的控制器如经典三回路自动驾驶仪结构图7所示。

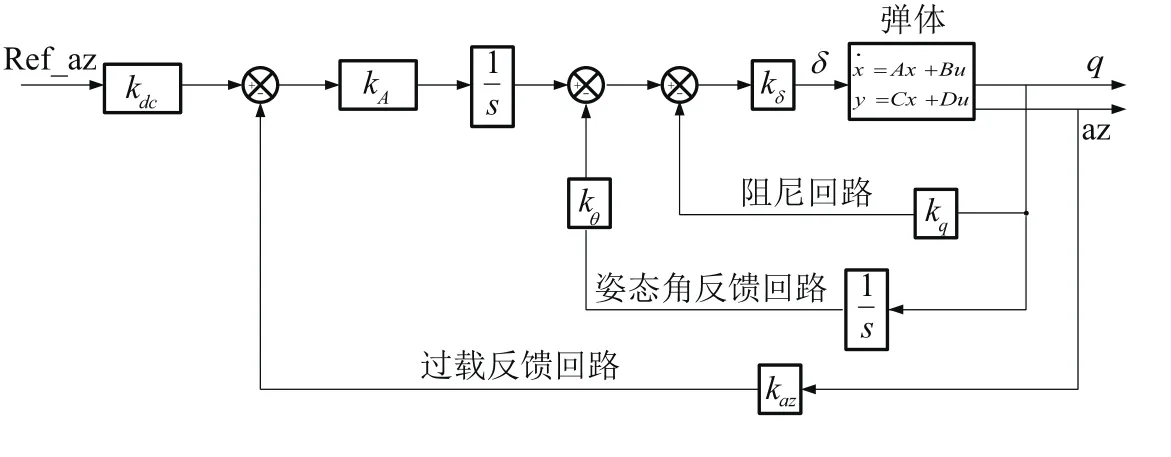
图7　三回路自动驾驶仪结构Fig.7 Structure of three loops autopilot

选用相同状态的特征点进行传统控制器参数设计，并达到与 μ综合控制器设计结果近似的控制性能，然后从频域上比较两种方法的结构奇异值特性。图8给出了μ综合控制器和传统控制器构成的闭环系统结构奇异值随频率变化特性图。

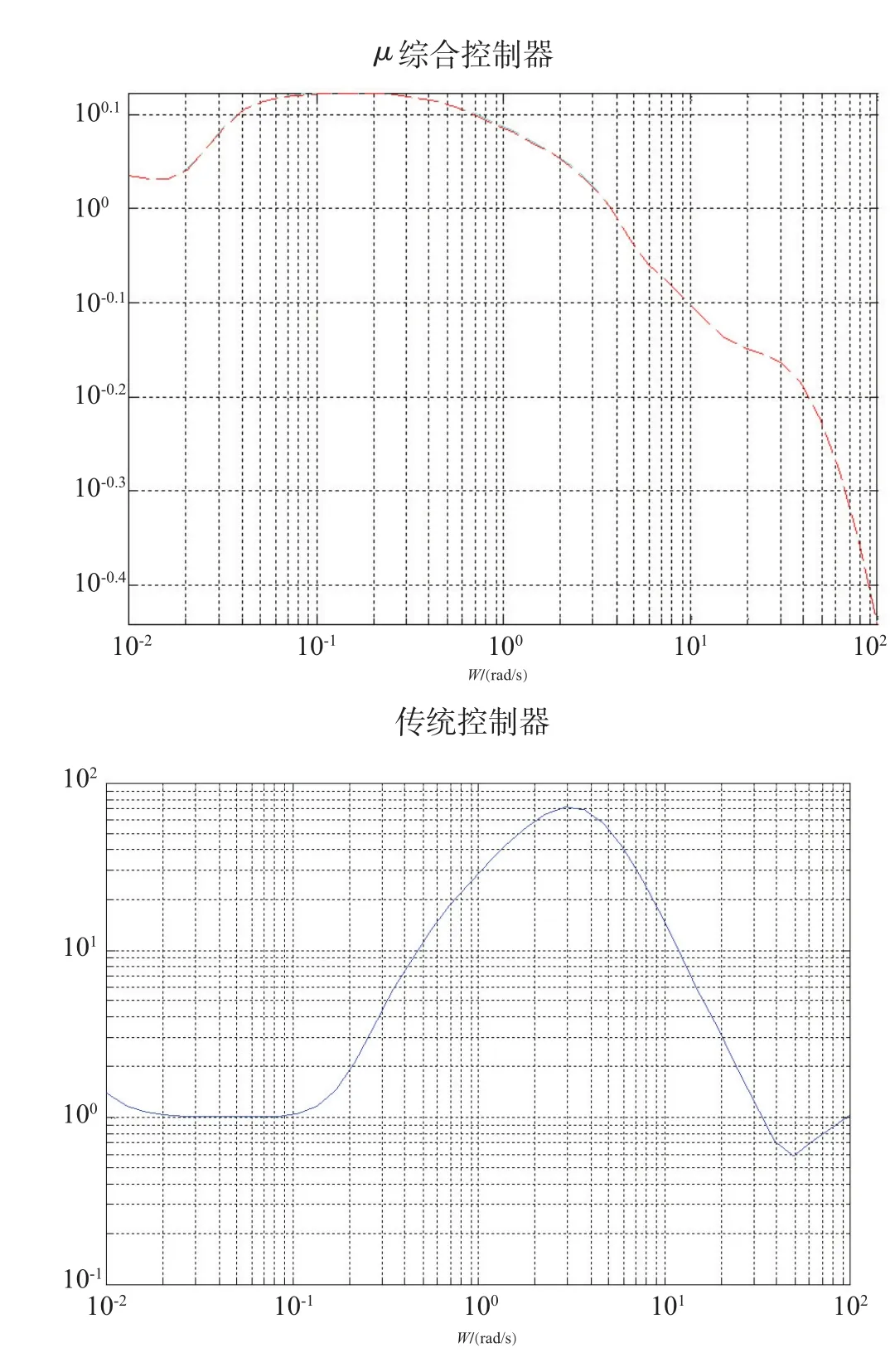
图8　μ综合控制器与传统控制器结构奇异值比较Fig.8 Compare ofμsynthesis controller and PI controller

由图8可见，在0.01～100rad/s范围内（尤其是驾驶仪的工作频带1～100rad/s）采用 μ综合控制器的闭环系统结构奇异值明显小于传统控制的闭环系统，尤其在中频段更加显著，这意味着前者对建模不确定性具有更好的抑制作用。

从以上分析可见，利用μ综合方法设计出与传统控制器相比在同等控制性能下具有更好的鲁棒性或者在同等鲁棒性指标下具有更优的控制性能的控制器是完全可能的。

4　结论

本文通过建立基于状态空间的导弹纵向弹体模型，采用 μ综合方法进行了自动驾驶仪的设计，与传统的经典控制方法相比，对于含有各类有界的参数和非参数不确定性的被控对象，结构奇异值方法无保守性地解决了鲁棒性问题。并且 μ分析方法比古典控制理论中的增益裕度、相位裕度方法要更具有普遍性， μ综合方法不仅可以解决动态控制器中的参数变化问题，还可以处理在被控对象模型中的不确定性以及回路中任何位置的参数摄动问题。在任何使闭环系统不稳定的情况下，通过对结构奇异值的分析能够定量地、无保守性地给出其稳定性和鲁棒性能的裕量。从仿真结果可以看出用μ综合的方法设计的控制器，不但能保证闭环系统的鲁棒稳定性，而且还能保证系统摄动情况下的鲁棒性能，这是其它控制方法所不能及的，从而体现了μ综合的优越性。

参考文献

[1]周克敏,J C Doyle,K Glover.鲁棒与最优控制[M].国防工业出版社.2002:138-139.

[2]Lee K W,Singh S N.Global robust control of an aeroelastic system using output feedback[J].Journal of guidance,control and dynamics,2007,30(1):271-275.

[3]史中科.鲁棒控制理论[M].国防工业出版社.2003: 187-191.

[4]Spillman M S.Robust longitudinal flight control designusing linear parameter-varying feedback[J].Journal of guid ance control and dynamics.2000,23(1):101-108.

[5]Curits P Mracek,D.Brett Ridgely.Missile longitudinal autopilots:comparison of multiple three loop topologies [C].AIAA2005-6380:5134-5161.

[6]Trevor J Birch,Kristian Petterson.CFD predictions of square and elliptic cross-section missile configurations at supersonic speeds[C].AIAA2004-5453:1-18.

中图分类号：TP273.7

文献标志码：A

文章编号：2095-8110（2014）03-0037-05

收稿日期：2014–04–25；

修订日期：2014–06–10。

作者简介：王建琦(1977–），男，博士，高工，主要从事飞行控制系统设计。E-mail:wangjianqi88@hotmail.com

Autopilot Design Based on Method of μ Synthesis

WANG Jian-qi,YANG Yu-rong,ZHENG Kun-peng
(ChinaAirborne MissileAcademy,Luoyang 471000,China)

Abstract：Method ofμsynthesis based on self-contained structured singular value theory provides a resolution for control system with uncertain character.It makes the control system to have enough robustness and optimal control performance.When the missile is flying in the dense aerosphere,the autopilot is such a control system facing a lot of uncertain elements.To obtain the optimal robustness in such case,the method ofμsynthesis is used to design the autopilot in this paper.Also the results of simulation are tested and analysed.And the final analysis indicates the adopted controller has a better robust effect than the traditional PI controller.

Key words:Robust Control;Method ofμsynthesis;D-K iteration algorithm;Autopilot