基于比例导引角度线性化的无人机避障研究

杨秀霞，刘小伟，张 毅

（海军航空工程学院控制工程系，山东烟台264001）

基于比例导引角度线性化的无人机避障研究

杨秀霞，刘小伟，张 毅

（海军航空工程学院控制工程系，山东烟台264001）

基于无人机与障碍物之间的几何关系，在极坐标系下建立了无人机与障碍物之间的运动学方程，通过引入基于角度线性化的比例导引律，使无人机能够顺利避开障碍物。引入的基于角度线性化的比例导引律是关于无人机相对速度航向角与避障点视线角的函数，由比例函数及偏差函数组成。为解决初始时刻相对速度航向角不满足引入导引律的问题，在调节函数中加入了指数项。通过稳定性证明，得到了满足要求的导引律参数取值范围。最后对设计的避障算法进行了仿真，仿真结果验证了算法的有效性。

角度线性化；比例导引；偏差函数；避障

0 引言

目前，无人机在军事及民用领域已得到越来越广泛的应用。如何使无人机能够安全导引到目标并顺利避开动态障碍物是众多学者研究的重点课题。

最早对这一问题开始研究的是O.Khatib[1]、Erdmann和Lozano-Perez[2]等人。后来，学者们把在静态环境下得到成功应用的路径规划及避障方法推广到动态环境中去，如在文献[3]中提到了确定及随机的路径地图方法，在文献[4]中通过考虑机器人及障碍物的速度，并加入到势能函数的构造中，得到适用于动态环境的势场法，在文献[5]中通过动态窗口方法进行路径规划及避障。这些方法在静态环境下得到较好的结果，但是在动态环境下，尤其是应用于无人机高速运动这一特殊情况下，避障效果并不理想。其原因主要是在动态环境下，碰撞判断及避障情况下对速度的控制与静态环境相比存在较大区别。

为解决动态环境下的碰撞判断问题，文献[6]、[7]提出了基于运动学方程的碰撞判断方法。文献[6]定义了碰撞锥的概念，依据视线的距离及角速度来确定碰撞条件。在文献[7]中基于视线角速度方程，对直接碰撞和间接碰撞进行了比较。

同时考虑到动态环境下障碍物速度变化的问题，学者们提出了速度障碍的概念。例如文献[8]在考虑运动障碍物速度的基础上进行碰撞锥的构建，在此基础上，通过使机器人的速度转移到碰撞锥之外达到避障目的，但是对障碍物的速度要求必须是线性的。为解决障碍物速度为不定值的避障问题，文献[9]通过对某一时刻，在考虑无人机及障碍物相对位置情况下，对可能的碰撞速度进行时间积分，得到非线性速度障碍集进行避障。同时考虑到多无人机之间的避碰问题，文献[10]提出了互惠速度障碍的概念，即两个即将相碰的障碍物之间互相主动避碰，达到避碰目的。

在对上述方法分析和总结的基础上，本文提出了基于角度线性化的比例导引无人机避障算法。首先在极坐标系下建立无人机与障碍物的相对运动学方程，通过引入基于角度线性化的导引律进行避障算法设计。考虑到一般情况下无人机相对速度初始航向角不满足给定导引律的问题，通过引入指数偏差函数对航向角进行调节，使无人机的最终稳定航向角达到避障要求。通过对设计算法稳定性证明，得到了满足要求的各个参数取值范围。最后本文利用Matlab对设计的避障算法进行了仿真，结果验证了算法的有效性。

1 几何关系及运动学方程

1.1 问题描述

当无人机与障碍物在惯性空间运动时，建立无人机与障碍物的几何关系示意图，如图1所示。无人机的速度为vuav，方向为ψuav，障碍物的速度为vobs，方向为ψobs。无人机相对障碍物的速度为vrel，方向为ψrel。由速度障碍原理，通过扩大障碍圆半径，把无人机简化为质点U，基于质点U及障碍圆切线UB、UA建立碰撞区域UAB。若相对速度vrel位于碰撞区域UAB内，则存在碰撞危险，因此需要调整无人机的速度的大小及方向，使无人机的相对速度vrel位于碰撞区域UAB之外。调整时，一般考虑相对速度vrel角度变化最小即避障完成时间短、偏离原目标轨迹短原则，结合图1，选取避障切线为UB，即避障点为B。

本文提出的避障算法是设计关于无人机相对速度的航向角ψrel的导引律，使无人机能够到达避障点B，且相对速度方向ψrel与切线UB方向θBu相等，确保避障完成。

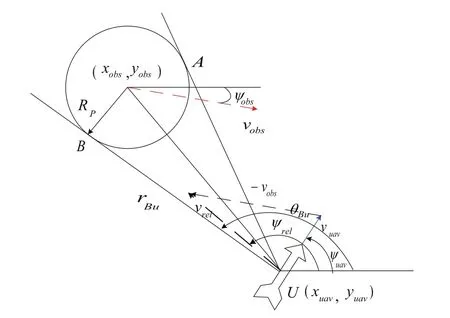
图1 无人机与障碍物几何关系示意图Fig.1 The scheme of geometric relation of UAV and obstacle

1.2 建立运动学方程

由于障碍圆是刚性圆，因此B点的速度大小及航向角与圆心一致，因此可得无人机U与B点之间的距离及视线UB的角度θBu的变化率为：

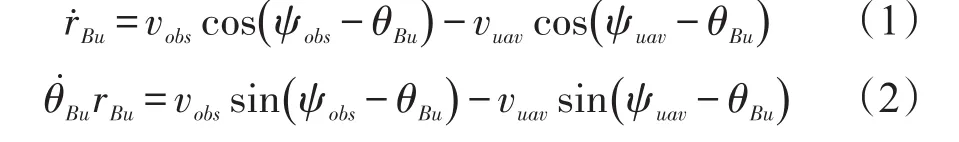
为研究方便，我们建立无人机与障碍物的相对运动方程，此时无人机以相对速度vrel飞向避障点B：

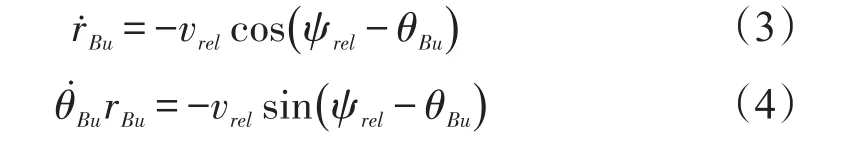
式（3）给出了无人机与避障点B之间的距离变化关系，式（4）给出了无人机与避障点B之间的视线角的变化方程。

2 角度线性化比例导引律

本文基于角度线性化比例导引律对避障算法进行设计。选择比例导引律最基本的定义，即相对速度vrel的航向角速度与目标视线UB的角速度成比例，即。

其中N为比例导引系数，满足N＞1。考虑初始状态有：

1）如果ψrel(t0)=NθBu(t0)，则比例导引律可表示为：ψrel(t)=NθBu(t)；

2）如果 ψrel(t0)≠NθBu(t0)，则比例导引律可表示为：

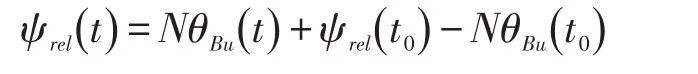
设c=ψrel(t0)-NθBu(t0)，则相对速度航向角可表示为：

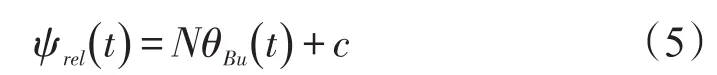
c对无人机的飞行曲线有较大的影响，用来控制曲线曲度。

基于导引律（5），则式（3）、式（4）可表示为：

当引入比例导引律时，要求在初始时刻ψrel(t0)满足：

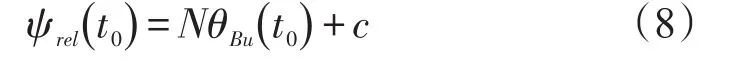
但是，在大多数情况下，当选定参数N及c后， ψrel(t0)并不满足式（8），因此引入的比例导引律并不能直接应用。

为解决这个问题，本文引入前置调节过程。在调节过程中，通过调节相对速度的航向角使其满足式（8）。

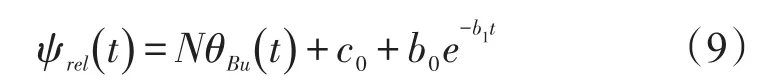
通过选择合适的参数b0，使ψrel(t0)满足：

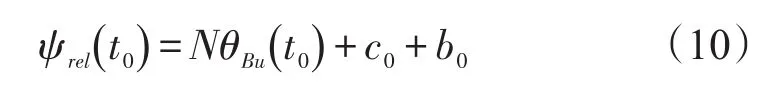
引入指数函数的目的是利用指数函数随时间的衰减特性来调节相对速度的航向角，这样在相对速度下，无人机的相对飞行轨迹就经过两个过程：

1）基于时变偏差函数的飞行过程，也就是前置调节过程，相对飞行轨迹以给定的曲率飞行，同时曲率半径是时变的。

2）基于常值偏差函数的飞行过程，当调节函数等于零时，比例导引中偏差值为常值，随着导引律的作用，相对速度航向角趋向于定值，并且到达目标点。此结论的证明见下节。

3 稳定性证明

基于导引律（9），则式（3）、式（4）可表示为：

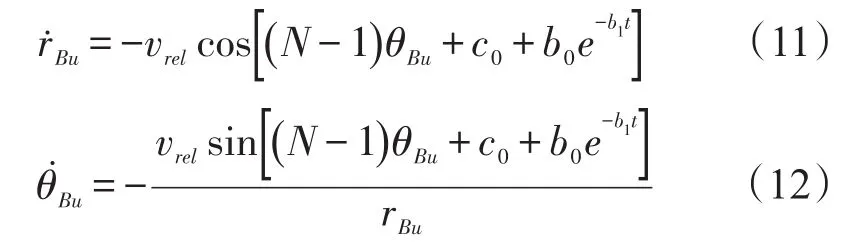
由分析知，随时间t→∝，指数项b0e-b1t→0。

因此由式 （12） 得， θBu的平衡点为：或者

基于线性理论，有：

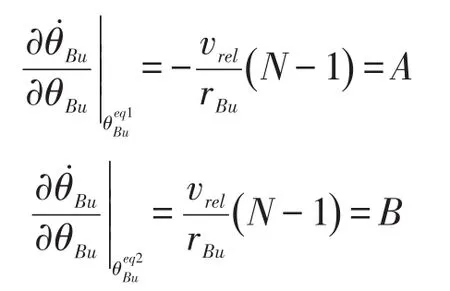
由vrel＞0，rBu＞0，N＞1，知 A＜0,B＞0,因此可得为全局稳定点，即随时间 t→∝，。

因此，由上面分析可知，当无人机到达避障点B时，相对速度航向角，若等于避障点B对应的切线角θtan，则避障完成。

因此，避障算法设计如下：

1）当无人机发现障碍物时，若相对速度位于避障锥内，需进行避障。考虑原路径是基于最终到达目标设计的，因此对路径的改变越小越好。因此，基于相对速度角度变化最小原则，选择相对速度调整方向。针对图1，选择相对速度调整方向为切线UB，因此避障点为B。

2）计算避障点B对应的障碍圆切线角度θtan。

3）设计线性比例导引律如式（9）所示，确定参数N、c、b0、b1，使导引律满足初始条件式（10）及使相对速度稳定航向角ψrel() tf与避障点B对应的切线角相等，即。

4 无人机航向角控制

避障算法设计的是关于相对速度航向角ψrel(t)的导引律，需要转换成与无人机航向角ψuav的关系。假设无人机速度大小不变，障碍物匀速运动。建立速度关系示意图如图2所示。

图2 无人机与障碍物速度关系示意图Fig.2 The scheme of velocity relation of UAV and obstacle

设vrel与vuav之间的夹角为α，vuav与vobs之间的夹角为β，则由正弦定理得：

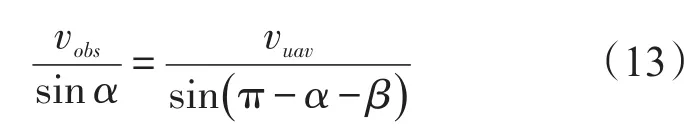
又知 β=ψuav+ψ0bs，代入式（13）得：

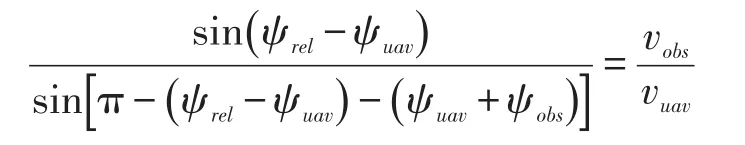
即：

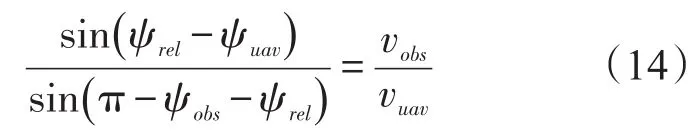
由vuav、vobs、ψobs为常值，可知ψuav为：

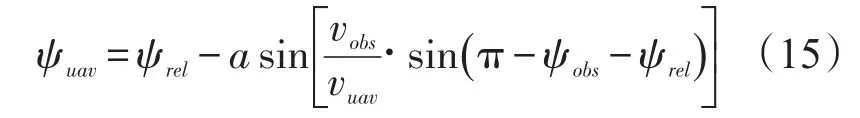
ψuav、ψobs、ψrel均为标量正值。

因此，若知道了ψrel的变化规律，就知道了ψuav的变化规律。

5 仿真分析

为验证上述算法的有效性，对算法进行仿真。

条件1，假设障碍物为静止，vobs=0m/s。

取障碍物坐标为xobs0=200km，yobs0=200km，无人机坐标为xuav0=0km，yuav0=0km，无人机初始航向角为 ψuav0=0.8/rad ，速度为vuav0=200m8/s，为显化避障效果，假设扩大后的障碍物圆半径RP=100km。比例导引系数N=3，无人机避障路径如图3所示。

图3 无人机避开静态障碍物示意图Fig.3 The scheme of UAV avoiding static obstacle

条件2，假设障碍物为运动障碍物，vobs=80m/s ，ψobs=0/rad 其余条件不变，则无人机避障示意图如图4、图5所示。

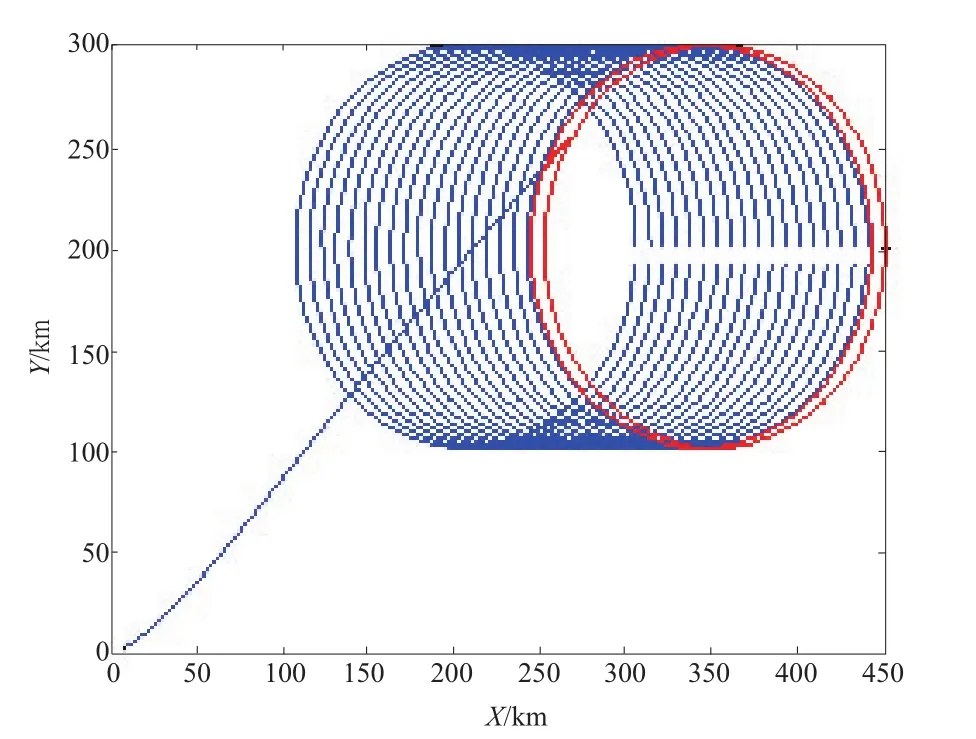
图4 无人机避开动态障碍物示意图（一）Fig.4 The scheme of UAV avoiding dynamic obstacle(1)

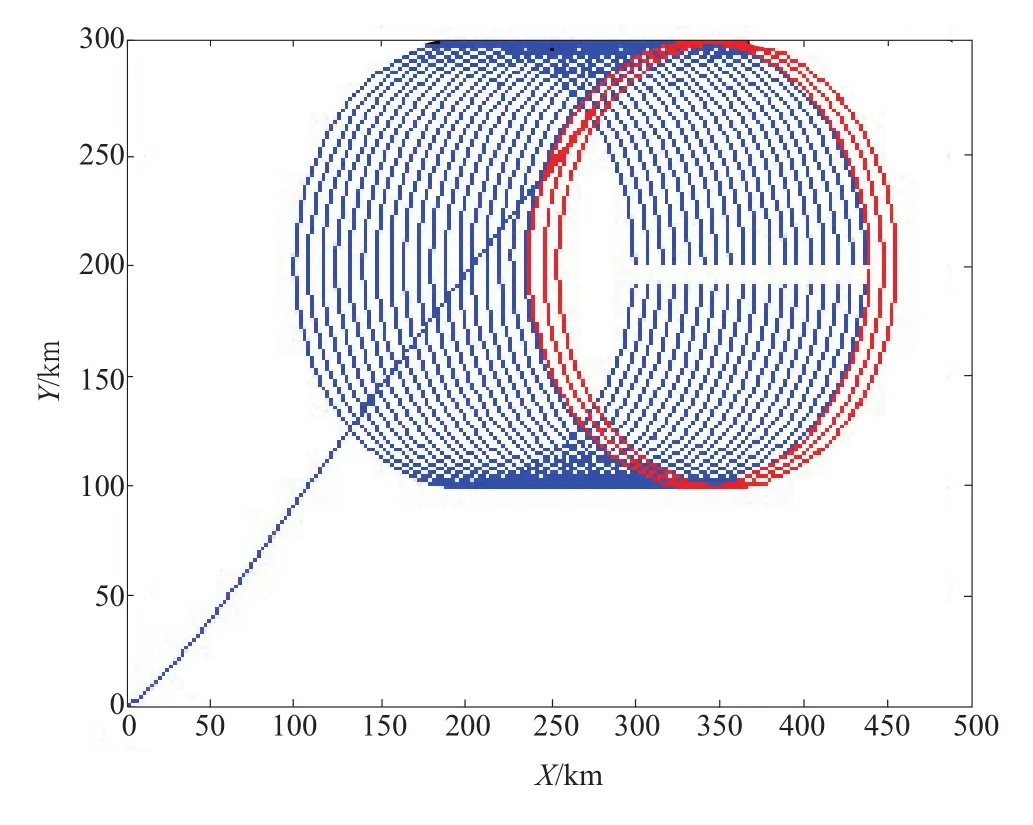
图5 无人机避开动态障碍物示意图（二）Fig.5 The scheme of UAV avoiding dynamic obstacle(2)

图4所示为无人机与障碍物相切示意图，图5所示为无人机与障碍物相切后继续运动，即障碍物继续沿X轴水平向右运动，无人机以ψuav(tf)角度匀速运动一段时间后示意图，由图5知下一刻无人机与障碍物分离，知无人机成功避开运动障碍物。

由仿真结果图3、图4、图5可知，设计的避障算法可成功避开静止及运动障碍物，证明了设计算法的有效性。

6 结论

本文基于无人机与障碍物之间的几何关系，得到无人机与障碍物在极坐标系下的运动方程，通过引入线性比例导引律，设计避障算法，仿真结果显示无人机能够顺利避开静态及动态障碍物，证明了算法的有效性。

本算法的实现仅需要知道障碍物及无人机的位置及速度这4个参数，因此，算法操作起来比较方便。下一步的工作是该算法扩展到三维空间，并对障碍物是变加速的情况进行研究。

[1] O Khatib.Real time collision avoidance for manipulatorsand mobile robots[J].The International Journal of Robotics Research,1986,5(1):90–98.

[2] M Erdmann,T.Lozano-Perez.On multiple moving objects[J].Algorithmica,1987,2(1):477–521.

[3] K Fujimura,H Samet.Roadmap-based motion planning in dynamic environments[J].IEEE Trans.Robot, 2005,21(5):885–897.

[4] S Ge,Y Cui.Dynamic motion planning for mobile robotsusing potential field method[J].Auton Robots,2002, 13(3):207–233.

[5] M Seder,I Petrovic.Dynamic window based approach to mobile robot motion control in the presence of moving ob stacles[C].Conf.Robot.Autom,Roma,Italy, 2007:1986–1992.

[6] A Chakravarthy,D Ghose.Obstacle avoidance in dynamic environment:a collision cone approach[J].IEEE Trans.Syst.,Man Cybern.A,Syst.,Humans,1998,28 (5):562–574.

[7] F Belkhouche,B Belkhouche.K inematics based charac terization of the collision course[J].Robot.Autom,2008, 23(2):127–136.

[8] 朱齐丹,钟训昱,张智.基于速度变化空间的移动机器人动态避碰规[J].机器人,2009,31(6):539–547.

[9] F Large,S Sckhavat,Z Shiller,C Laugier.Using nonlinear velocity obstacles to plan motions in a dynamicenvironment[C].Conf.Control,Autom,Robot.Vis, 2002:734–739.

[10] van den Berg J,Lin M,Manocha D.Reciprocal velocity obstacles for real-time multi-agent navigation[C].2008 IEEE International Conference on Robotics and Automation,2008:1928–1935.

Study onAngle Linearization of Proportional Navigation-based CollisionAvoidance for UAV

YANG Xiu-xia，LIU Xiao-wei，ZHANG Yi
（NavalAeronautical andAstronautical University Department of Control Engineering，Shandong Yantai 264001，China）

Based on the geometric relationship between the UAV and the obstacles,we estublish the kinematics equations between the UAV and the obstacles in polar coordinates.By introducing a navigation law of angle linearization of proportional navigation,we design an algorithm of collision avoidance to make the UAV successfully avoid the obstacles.The angle linearization of proportional navigation law is the function of the angle of the relative velocity of the UAV with the angle of the line of sight of the obstacle avoidance point,which is composed of the proportional function and the deviation function.To solve the problem that the angle of the relative velocity does not meet the law at the initial time,the paper adds exponential function in the deviation function.By proving the stability of the algorithm,we obtained the ranges of the parameters which meet the requirements.Finally,we make the simulation of the algorithm,and the simulation results show the effectiveness of the algorithm.

Angle linearization;Proportional navigation;Deviation function;Collision avoidance

V448.16

A

2095-8110（2014）03-0001-05

2014–05–06；

2014–06–27。

航空科学基金（20135584010）

杨秀霞（1975–），女，博士，硕导，主要从事飞行器导航制导与控制方面的研究。E-mail:yangxiuxia@126.com