GPS-RTK测量中坐标转换模型的适用性分析

江晓鹏 JIANG Xiao-peng；熊建华 XIONG Jian-hua

0 引言

GPS-RTK测量可以快速便捷地获得高精度的定位数据，在工程测量中应用越来越广泛，GPS-RTK技术与传统测量技术相比，RTK实时动态测量工作效率高、灵活度大[1]。精度作为测量成果的重要指标，因此GPS-RTK作业精度是一个不容忽视的问题，坐标转换参数的选取作为RKT野外测量的基础[2]，转换参数如果超过误差范围，那么野外观测数据无论多么精确，都将导致错误的结果[3]，因此坐标转换参数的精确程度是影响RTK测量精度的关键因素，因此必须慎重选择好坐标转换模型。

1 GPS-RTK测量中坐标转换问题

GPS-RTK测量能够实时的获取精确的大地坐标值，其值由经纬度和大地高表示，而我国现在所采用的坐标系统一般为1980国家大地坐标系、1954北京坐标系、地方坐标系或GCS2000国家坐标系统，高程基准为1985国家高程基准或1956年青岛黄海高程基准[4]。因此为了在GPS-RKT测量过程中实时获取当地坐标值，就必须在作业前先求解出WGS-84坐标与当地坐标的转换参数，从而能够实时的将WGS-84坐标转到工程中所需要的地方坐标。然而在不同区域该转换参数不完全相同，为了提高RTK的测量精度，就必须求出适合本地区的坐标转换参数，但在坐标转换参数求取过程中也涉及到不同的坐标转换模型，不同转换模型其适用性也不一样，得到的坐标精度也不一。坐标转换流程如图1所示。

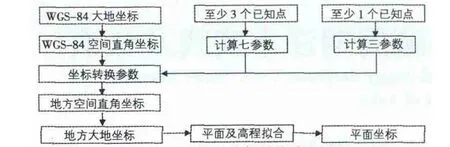
图1 坐标转换流程图

2 不同坐标转换模型及适用性分析

WGS-84坐标转换到地方平面直角坐标需要经过四个步骤[5]：WGS-84 坐标系中的大地坐标（B，L，H）84转换成空间直角坐标（X，Y，Z）84；WGS-84下的空间直角坐标值（X，Y，Z）84转换成为地方椭球下的空间直角坐标（X，Y，Z）80；地方空间直角坐标转换到（X，Y，Z）80地方大地坐标（B，L，H）80；最后通过地方大地坐标（B，L，H）80转换成为特定投影下的当地平面直角坐标及高程（x，y，h）。

2.1 大地坐标系与空间直角坐标转换关系模型 大地坐标(B，L，H)与空间直角坐标(X，Y，Z)的转换关系如下：X=（N+H）cosB cosL X=（N+H）cosB sinL

公式（1）中N为该点卯酉圈曲率半径，a为椭球体的长半径，e为椭球体的第一偏心率。

2.2 七参数坐标转换模型 坐标转换其实就是不同椭球基准间的转换，其方法有很多，归纳起来国内外坐标变换的成熟模型主要有布尔沙-沃尔夫（Bursa-Wolf）模型、莫洛登斯基-巴代卡（Molodensky-Badekas）模型、范士（Veis）模型等模型。为了适应我国地心坐标变换参数，我国常用的是Bursa模型，又称七参数法，是一种空间直角坐标系的转换模型。其转换模型如下：

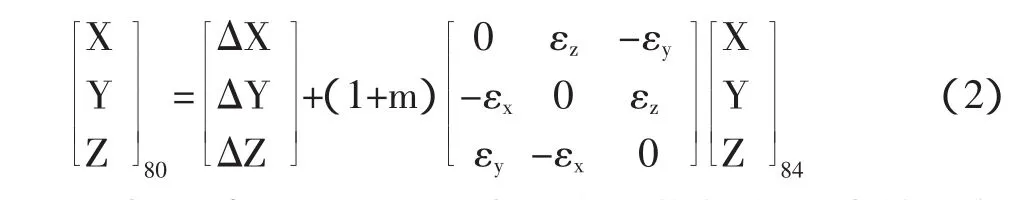
公式（2）中 ΔX、ΔY、ΔZ为三个平移参数，m 为缩放参数，εx、εy、εz为三个旋转参数，根据以上模型，可转换成为矩阵形式观测方程，通过最小二乘原理获得最优参数估计值。七参数法转换较为严密，一般用于转换精度要求较高的大型测量项目中，测区范围大求取其坐标转换参数至少需要三个以上的高精度已知控制点，相应的WGS-84坐标点也必须是经过数据平差后静态GPS控制点，这样才能保证两套坐标的已知控制点的精度，坐标转换参数的求解质量还与所使用的公共控制点个数和几何图形结构有关[6]。在解算其参数过程中，如果有较多的控制点，可根据控制点精度、个数和图形结构设计多种方案，最终依据计算的残差大小来确定最终转换参数方案，因此已有控制点的精度以及正确选用已有控制点对于七参数的转换是极其重要的。

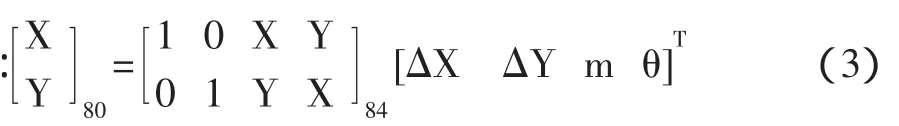
公式（3）中ΔX、ΔY为平移参数，m为缩放参数，θ为旋转参数。四参数坐标转换方法是一种二维平面的坐标转换，是平面直角坐标系的转换模型，不对其高程进行拟合处理，在实际工作中，GPS-RTK测量的坐标参数求取，较多选择的是平面转换模型和高程拟合模型共同完成坐标转换。即“四参数+高程拟合”的方法[7]，该求取坐标转换参数的方法只适用于小区域测量（10km2以下），至少需要两个已知点来求取其坐标转换参数。

2.4 三参数坐标转换模型 如果测区范围较小，可以认为两个空间直角坐标系各坐标轴相互平行且其尺度比基本相同，就可以用简便的转换模型，即在七参数法的基础上的，忽略旋转角和尺度因子的影响，坐标系之间的变化就被简化为两个坐标原点之间的平移（ΔX，ΔY，ΔZ），即形成所谓的三参数法，该模型如下：

公式（4）中 ΔX、ΔY、ΔZ 为平移参数，其实三参数法是七参数法的一种特例，根据实际工作中的应用，该模型随着移动站离基准站距离的增加其精度逐渐降低，因此仅适用于精度要求较低的小区域的测量（1km2左右）。

3 总结

综上所述，不同的测量范围可采取不同的转换模型来求取坐标转换参数，我们应该根据各项工程的实际情况和具体要求，选择适合本工程的坐标转换参数计算方法，求取最准确的坐标转换参数，当测区范围较大时有必要进行分区求取坐标参数[8]。当然RTK测量求取转换参数时还需要考虑一些特殊情况，如转换参数的控制点精度问题、控制点的系统误差问题，也一定程度上影响着坐标转换参数的精度[9]。计算准确的坐标转换参数对于GPS-RTK测量成果至关重要，实际应用中应该根据实际情况联测足够多的已知点，充分检核坐标转换参数的正确性。只有充分保证测量的准确性，才能更好地应用GPS-RTK技术来提高我们的工作效率。

[1]徐绍铨,张华海,杨志强等.GPS测量原理及应用[M].湖北：武汉大学出版社，2008.

[2]马捷.提高GPS-RTK测点精度和可靠性的探讨[J].中州煤炭,2006（2）：18-19.

[3]丁文利,王怀念,黄良.动态 GPS(RTK)测量的精度分析[J].地矿测绘,2004(2)∶16-17.

[4]牛丽娟.测量坐标转换模型研究与转换系统实现[D].长安大学,2010.

[5]杨红艳,高霞,赵惊雷,张予杰.坐标转换参数不同的求取方式对RTK测量影响的对比分析[J].全球定位系统,2005∶14-17.

[6]潘宝玉,张西恩,李宏伟.提高RTK测量成果精度的技术关键[J].地矿测绘,2003(3)∶1-3.

[7]陶长志.浅谈在工程测量中RTK测量坐标转换参数的选择[J].测绘与空间地理信息,2011(3)∶86-87.

[8]孙晓光.WGS-84与地方坐标系转换参数的优化选择[J].测绘与空间地理信息,2007(2)∶152-154.

[9]田泽海.GPS-RTK测量求取坐标转换参数的探讨[J].测绘与空间地理信息,2008(2)∶52-54.