精确提取闪变波动分量的新方法

任祖华，王柏林

（河海大学能源与电气学院，南京 210098）

冲击性、非线性负荷的投入使用，不仅给电网带来大量的高次谐波和间谐波，同时，电弧炉、轧钢机等干扰性负荷给电力系统造成明显的电压波动，除了影响其他用电设备的正常运行，还可能引起照明灯光的闪烁，即闪变。国内外闪变仪测量电压波动的主要方法有平方检测法、整流检测法和有效值检测法，这些方法对于稳定的单一频率成分的调幅波检测较为准确，而在处理时变的电压波动信号和含有间谐波引起的闪变时，可能会带来误差。电压闪变是由电网电压的幅值波动变化引起的，由于其明显的调制特性，通常使用调幅波模型对其进行分析计算,即将电压波动看作是以工频电压为载波，其电压的均方根或峰值受到以电压波动分量作为调幅波的调制。目前大量的闪变检测研究就是针对这种调幅波模型，主要分为包络线检测和频率幅值确认两大类,其中Hilbert变换是常用的包络检测方法，Hilbert变换是一种非平稳信号处理方法，能快速提取出信号的包络，但当信号畸变程度较大时会影响测量精度，需首先进行去噪处理。文献[1～2]就是利用Hilbert变换方法提取电压波动信号的包络线，将其用于调幅波闪变信号检测。文献[3～4]采用基于能量算子和盲信号分离的方法检测信号包络，其算法复杂性和计算量增大。事实上，间谐波的引入也会导致电压波形的均方根值和峰值发生波动，叠加了间谐波后的信号包络会发生波动，因此间谐波也能导致闪变。对于间谐波引起的闪变，文献[5～6]分别提出二次采样、半周期峰值采样检测间谐波闪变的新方法，但都是针对含有单个间谐波成分的分析。

本文讨论了调幅波和间谐波所引起电压幅值波动；并详细分析了当含有高次谐波和间谐波时，Hilbert变换检测包络线所存在的问题。在此基础上，提出了一种基于极值点插值的包络线检测方法，此包络线不受高次谐波的影响，能同时反映调幅波和间谐波所引起的峰值波动，对提取的包络线进行高精度FFT可以直接得到精确的闪变幅值和频率。

1 电压波动信号模型

电压闪变信号具有明显的幅值调制特性，因此通常使用调幅波模型对其进行分析计算,而间谐波的引入也会导致电压波形的均方根值和峰值发生波动，进而引起闪变。同时电力系统中还存在大量的高次谐波成分，在闪变检测时也必须对其所产生影响予以考虑。

含有高次谐波、间谐波和调幅波的电压波动信号可描述为

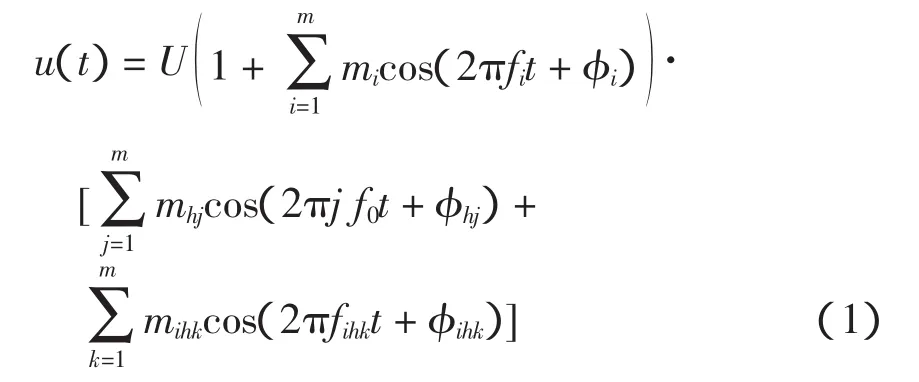
式中：U和f0分别为基波电压幅值和频率；mi、fi、φi分别为第i个调幅波的相对幅值、频率和相位；mhj、φhj分别为第j次谐波的相对幅值和相位；mihk、fihk、φihk分别为第k个间谐波的相对幅值、频率和相位。比如，调幅波为8Hz的正弦信号，载波信号为基波同时叠加3次、5次谐波以及58Hz、142Hz间谐波的电力信号波形如图1（a）所示（假设基波幅值为1）。可见，电压幅值有明显的波动，波动信号包络如图1（b）所示，波动频率为8Hz，相对幅值为0.06。下面详细分析引起电压波动的因素。

图1 电压波动信号及其包络Fig.1 Fluctuational voltage and its envelope

1.1 调幅波所引起电压波动

调幅波m cos（2πfmt+φ）对基波调制，所引起的电压幅值波动频率为fm，幅值为m。图2（a）为8 Hz的调幅波引起的电压波动，波动频率为8Hz，相对幅值为0.02。

1.2 间谐波所引起电压波动

假设间谐波的频率为fih=hf0±fm，h=1，2，…（即间谐波和与之最邻近的h次谐波的频率之差为fm），间谐波的相对幅值为mih，则包含基波和单一间谐波的电压信号为

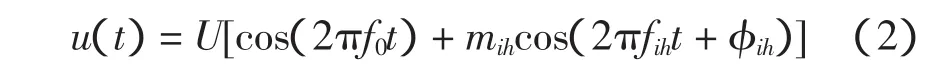
闪变频率计算式为

图2(b)为58Hz和142Hz间谐波所共同引起的电压波动，波动频率为8Hz，相对幅值为0.04。

图2 调幅波和间谐波所引起的电压波动Fig.2 Voltage fluctuation caused by the amplitude modulation signal and interharmonics

依据第1.1节和第1.2节的分析，可得如下结论。

（1）幅值为m、频率为fm的调幅波产生的电压幅值波动和幅值同为m、频率为fm的间谐波作用所产生的电压幅值波动相同。

（2）相同幅值的间谐波，只要其频率fm（即间谐波频率和与之最邻近的h次谐波的频率之差）相同，则所引起的电压幅值波动就相同。

因此，图1中的电压幅值波动是调幅波和间谐波共同作用的结果。

2 Hilbert变换包络线检测存在的问题

Hilbert变换是常用的闪变包络线检测方法，当不考虑谐波和间谐波的影响时，其对于只含有调幅波分量的电压包络检测是有效的。然而，当闪变信号中含有高次谐波时，采用Hilbert变换检测出的包络线除闪变信号外，也将含有高次谐波分量。若直接采用含有谐波的包络估计闪变的参数,会带来较大的误差[3]。

2.1 高次谐波的影响

对于含有谐波和调幅波的电压信号为

式中：A（t）为包含调幅波分量的信号包络；h为谐波次数。

其Hilbert变换为

则

可见，式（6）所示包络线除调幅波之外，还含有第h-1次谐波分量，因此必须对包络线进行滤波，可通过低通滤波器将高次谐波去除，但往往会因为数据长度有限，滤波器输出的前一段数据不稳定，使得闪变包络波形很短或很不完整。

2.2 间谐波引起的闪变分量

对于间谐波引起的电压波动信号为

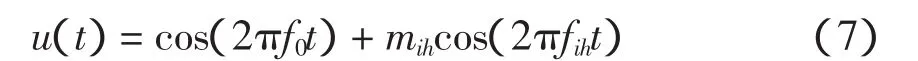
式中：mih为间谐波相对幅值；fih为间谐波频率。

其Hilbert变换为

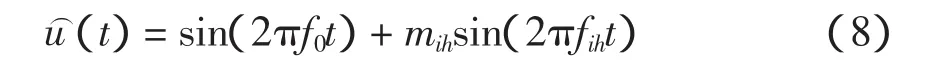
则

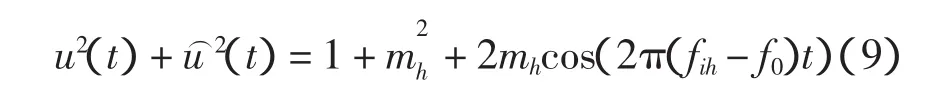
Hilbert变换检测的包络线频率为|fih-f0|的间谐波分量，无法直接检测出频率为fb的闪变分量，

故Hilbert变换对于间谐波引起的闪变无法测量。

如图3（a）所示，电压信号中只含有单个频率的调幅波和基波成分时，Hilbert变换能准确检测出闪变包络线。而当闪变信号中含有3次和5次谐波时（相对幅值为0.05），采用Hilbert变换检测出的包络也含有高次谐波分量，如图3（b）所示，此时需通过滤波器将包络线中的高频分量滤除，才能得到闪变信号。如图3（c）和（d），电压信号除含有基波外，还分别含有58 Hz和142Hz的间谐波时，采用Hilbert变换提取的包络线频率分别为8Hz和92Hz，但实际上二者引起的闪变波动同为8Hz。

因此，有必要找到一种通用且简单有效的包络检测方法，使提取的包络线只包含闪变分量，不受高次谐波影响，同时对不同频率的间谐波所引起的闪变，也能直接提取出其闪变波动分量。

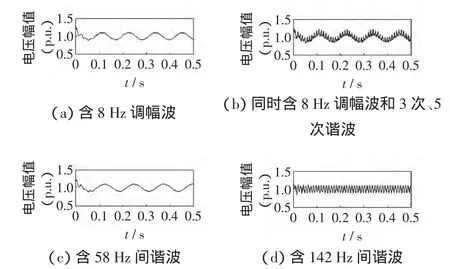
图3 Hilbert变换提取的电压信号包络Fig.3 Voltage envelope extracted by Hilbert transform

3 闪变包络线检测与参数估计

电压波动的定义为电压均方根值一系列相对快速或连续改变的现象，电压波动值为电压均方根值的两个极值Umax和Umin之差，如图4所示。因此，只要准确提取出波动信号v，即闪变信号的包络线，就能对该包络线进行频谱分析，得到闪变的幅值和频率信息。基于该思想，本文提出寻找极值点进行插值的包络线检测方法。

图4 电压波动的定义Fig.4 Definition of voltage fluctuation

3.1 极值点插值的包络线检测方法

步骤1寻找极大值点和极小值点序列。

在某一段时间内，对式（1）所示电压信号u（t）采样得到离散序列{u（i）}，i=1，2，…，n，对该电压采样序列求差分运算得序列{d（i）=u（i+1）-u（i）}，i=1，2，…，n-1，若k同时满足d（k）d（k+1）＜0和d（k）＞0，则k+1为一个极大值点所对应的编号，即u（k+1）为一个极大值点。同理，若l同时满足d（l）d（l+1）＜0和d（l）＜0，则l+1为一极小值点所对应的编号，即u（l+1）为一个极小值点。依照这种方法可求得极大值点序列{umax（i）}，i=1，2，…，p和极小值点序列{umin（j）}，j=1，2，…，q。

步骤2对极大（小）值序列进行筛选。

由于电压信号中含有多种频率的高次谐波，导致信号发生畸变，如图5所示，图（a）为含有6次谐波时的闪变信号，为方便观察，图（b）为截取其中一段进行的放大，可见极大值点不仅出现在信号峰值处，其他位置也有极大值点，因这些极大值点不能参与构建闪变信号的上包络线，称之为虚假极大值点，必须摒弃，筛选方法为：对极大（小）值点序列按照第1步方法再次求极值点。

步骤3对筛选后的极大（小）值点序列插值得到上（下）包络线。

三次样条插值是使用最为广泛的插值方法，它用分段三次多项式去逼近函数，可以给出光滑的插值曲线，它在每个子区间上都是二阶连续导数的三次多项式。对筛选后的极大（小）值序列进行三次样条插值，就可得到电压波动信号的上（下）包络线。

图5 含有高次谐波的闪变信号的极大（小）值Fig.5 Maximum(minimum)points of the flicker signal containing high harmonic

图6（a）为含有8.8 Hz调幅波，同时包含3次和5次谐波时，所提取的闪变包络线，与图3（b）比较，可见包络线中去除了高次谐波的成分；图6（b）为基波叠加58 Hz和142 Hz间谐波成分时，所提取的闪变包络线，与图3（c）和（d）比较，可见对于不同频率的间谐波也能准确反映出闪变波动分量。

图6 含有谐波和间谐波的电压闪变信号包络Fig.6 Flicker envelope of the voltage signal containing harmonics and interharmonics

以上可知，基于极值点插值的包络线检测方法不受高次谐波的影响，对于调幅波和间谐波引起的闪变都可以准确检测。

3.2 闪变参数估计

基于极值点插值方法提取的包络线，排除了高次谐波影响，只包含反映电压波动的闪变分量。由于提取的上、下包络线呈相同或相反的变化趋势，其包含的频域信息是相同的。为方便起见，采用上包络线进行高精度的加窗插值FFT来求取闪变幅值和频率。

4 仿真算例

4.1 简单闪变信号

选用表1中的参数对基波进行调制，假设电压工频信号幅值为1，频率为50 Hz，采样率为3 000Hz。本文算法估计的闪变幅值、频率如表1所示，与文献[4]采用Hilbert变换提取包络线的方法相比，幅值检测精度相当，频率精度进一步提高。

表1 简单闪变信号仿真参数Tab.1 Simulation parametersof simple flicker signal

4.2 含间谐波的多频闪变信号

当电压信号中包含间谐波分量引起的波动时，采用Hilbert变换得到的包络线也将含有间谐波成分，使得闪变信号分量无法直接提取。基于本文方法提取的包络线将只包含闪变信号，同样可以提取出间谐波引起的闪变分量，用表2中的参数进行Matlab仿真，得到的闪变幅值、频率见表2。

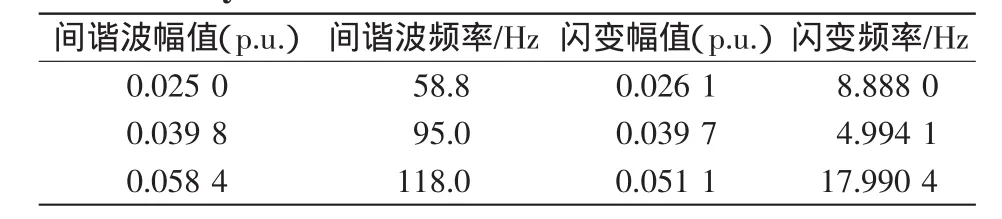
表2 间谐波闪变信号仿真参数Tab.2 Simulation parameters of flicker signal caused by interharmonics

4.3 含有高次谐波和间谐波的多频闪变信号

以下是当电压信号中含有3次和5次谐波（相对幅值为0.05），同时含有两个调幅波分量和两个间谐波分量时的情况，参数设置如表3所示。图7是基于极值点插值方法获得的包络信号，可见包络中含有多个频率的闪变信号，图8显示了包络信号中所包含的频率成分。对包络线采用高精度的FFT加窗插值算法，获得闪变幅值、频率的估计值如表3所示。

表3 含高次谐波和间谐波时多频闪变信号仿真参数Tab.3 Simulation parameters of multi-frequency flicker signal containing harmonics and interharmonics

图7 同时含有高次谐波和间谐波的多频闪变信号包络线Fig.7 Envelope of multi-frequency flicker signal containing harmonics and interharmonics

图8 多频闪变信号包络线的频谱Fig.8 Spectrum of multi-frequency flicker envelope

5 结语

本文对调幅波和间谐波所引起电压幅值波动进行了分析，说明其与闪变之间的关系。并详细分析了Hilbert变换检测包络线所存在的问题，当电压信号中含有高次谐波和间谐波时，Hilbert变换得到的信号包络也将含有谐波和间谐波分量。本文提出一种通用并且简单有效的包络检测方法－基于极值点插值的包络线检测，使得提取的包络线只包含闪变分量。此包络线不受高次谐波的影响，能同时反映调幅波和间谐波所引起的波动，对提取的包络线进行高精度FFT可直接得到精确的闪变参数，仿真验证了算法的有效性。

[1]王志群，朱守真，周双喜（Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi）.Hibert变换求取电压闪变有关参数（Parameter estimation of voltage flicker through Hilbert transform）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（5）：34-37，66．

[2]魏晓璞，徐永梅，郭春林，等(WeiXiaopu，Xu Yongmei，Guo Chunlin，et al）.基于Hilbert变换与Pisarenko谐波分解的电压闪变参数估计（Parameter estimation of voltage flicker based on Hilbert transform and Pisarenko harmonic decomposition）[J].电力系统保护与控制（Power System Protection and Control），2010，38（6）：26-34.

[3]吴昊，戴本祁，居继涛（Wu Hao，Dai Benqi，Ju Jitao）.一种电压闪变实时检测的新方法（A novel real-time detection of voltage flicker）[J].电力系统保护与控制（Power System Protection and Control），2009，37（8）：30-33.

[4]国添栋，王祁（Guo Tiandong，Wang Qi）.基于互信息最小化盲源分离准则的电压闪变检测方法（Detection of voltage flicker based on blind source separation of minimum mutual information）[J].电力系统保护与控制（Power System Protection and Control），2011，39（1）：57－61.

[5]季宇，孙云莲，王黎，等（JiYu，Sun Yunlian，Wang Li，et al）.基于半周期峰值采样的间谐波闪变算法（Research of voltage flicker caused by interharmonics based on halfcycle peak sequence）[J].电网技术（Power System Technology），2011，35（2）：66-70．

[6]马永强，周林，武剑，等(Ma Yongqiang，Zhou Lin，Wu Jian，et al）.间谐波引起的电压闪变测量新方法（A new approach to measure voltage flicker caused by interharmonics）[J].电网技术（Power System Technology），2010，34（5）：116-121.

[7]于静文，薛惠，温渤婴（Yu Jingwen，Xue Hui，Wen Boying）.周期性电压闪变信号数学模型频率特性分析（Frequency characteristic analysis of periodic voltage flicker signal mathematic model）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：72－77.

[8]周兆经，周文晖，李青（Zhou Zhaojing，Zhou Wenhui，Li Qing）.采用小波分解和同步检波的电压闪变信号检测新方法（A new method for the detection of voltage flicker using wavelet transform and synchronous detection）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2001，13（6）：23-27.