实变函数课程中点集与测度论教学改革初探
2014-04-14赵侯宇
赵侯宇
(重庆师范大学 数学学院,中国 重庆 401331)
点集和测度论作为实变函数课程中的重要组成部分,占据着重要位置.这部分内容具有理论性强、概念性多、比较抽象等特点,教师在进行授课时,如果只是一味的介绍,会导致学生产生厌学、抵触情绪,进而影响教学质量.如果在教学过程中做一些适当的引导,设置一些问题,让学生利用学到的知识自己探索,这样不仅使学生对知识掌握的更加牢固,也能使教学效果事半功倍.下面,我们通过几个定理和例题来解释教师在授课时的技巧和方法对学生影响的重要性.
例1 证明:P0∈E′的充要条件是在任意含有P0的邻域U(P,δ)(不一定以P0为中心)中,恒有异于P0的点P1属于E(事实上,这样的P1还有无穷多个);而P0∈E的开核的充要条件则是由含有P0的邻域U(P,δ)(同样,不一定以 P0为中心)存在,使 U(P,δ)⊂E.
分析:此题考查对几种点集的概念及相关性质的理解,主要包括开核、导集的定义及聚点的等价性质.事实上,只要熟练掌握这些概念,便能自然的推导出本题的结论.对于第一问,首先应该知道导集具体是什么样的集合,其次,利用导集中的点都是聚点联想到聚点的几个等价条件;对于第二问,只要知道了开核的定义,从此下手便可得到结果.针对上面的解题思路,只要教师在课堂上介绍这些集合的具体含义,并逐步引导学生推导出相关性质,相信学生会较顺利的完成该题.
证明:(1)若 P0∈E′,则对任一含 P0的邻域 U(P,δ),必有以 P0为中心的邻域 U(P0)⊂U(P,δ),所以存在 P1∈U(P0)⊂E∩U(P,δ),且 P1=P,即任何含有P0的邻域中含有一点P1异于P0而属于E.
反之,若一含有P0的邻域有异于P0的点P1属于E,当然对任一P0的邻域 U(P0)中也有异于P0的点P1属于 E,故 P0∈E′.
(2) 若 P∈E 的开核,则有 U(P0)⊂E.反之,若 P0∈U(P,δ)⊂E,必有U(P0)⊂U(P,δ)⊂E,即 P0∈E 的开核.
例2 关于康托三分集的学习.
分析:康托三分集是点集理论中的重要例子,如何讲好这部分内容是一个值得考虑的问题.教师可根据前面所学知识提出一些疑问,例如是否存在一个测度为零的完备集,并且它的基数是连续基数,借此引出康托集的概念.不妨利用几何的方式,即在黑板上画出康托集是如何构造出来的,随之将其中的性质介绍出来.比如每次取完中间一段区间后,剩下的每个区间长度是多少,它们之间是否有公共端点等,一步步的带着学生将康托三分集的性质得到,即:康托三分集是一个测度为零且具有连续基数的疏朗完备集.这样,学生在教师的指导下,一定能够较深刻的理解康托三分集的这些性质,课后,只要稍加复习,相信学生能够熟练掌握这些知识.
例3 设 E⊂Rq,存在两列可测集{An},{Bn},使得 An⊂E⊂Bn且 m(Bn-An)→0(n→∞),则 E 可测.
分析:此题考查对可测集的概念、性质以及测度、外测度的定义.具体来说,我们注意到An⊂E⊂Bn,并且告诉了我们An,Bn是两个可测集列,因此,可能会用到它们的交集.而交集显然比每一个集合都小,从而进一步可推导出Bn的交集与E的差集等结论,这样顺着此条思路,我们便可逐渐得到结论.该题是学生在对可测集和测度相关内容熟悉的基础上的一点推广,教师对这部分内容进行讲授时,特别是对可测集的性质的介绍,不妨让学生根据可测集的定义,自己去推导几个性质,以达到事半功倍的教学效果.

也可测.
例4 设{En}是[0,1]中可测集列,若 m(En)=1,n=1,2,…,则=1.
分析:本题考查可测集的相关性质,具体来说是指通过集合间的运算,运用可测集的性质进行讨论来完成证明.事实上,我们看到要证的测度为1,又观察到而每一个En的测度都是1,因此联想到它们之间的联系,不妨取其中一个集合E1,通过测度定义得到与之相关的等式,再进行计算,期间我们也能够发现整个区间[0,1]的测度是1,而每个En的测度是1,从而每个En的补集测度为0,这为我们提供了一些信息,证明过程中或许会用到,通过一步步的引导,相信学生能够做出此题.
证明:因为

而我们知道m(E1)=1,
所以
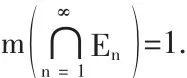
即本题结论得证.
通过对上面几个例题和定理的分析,我们可以看到对于点集和测度论这两部分内容及解题过程中应用的一些重要技巧和方法都是在对基础知识熟练掌握基础上才能够实现的,这个过程需要教师不断改进教学手段,通过引导、启发式教学,让学生自己探索,找到学习的乐趣,才能使学生对这门本就相对枯燥的课程产生兴趣,进一步又促使他们去探索、主动学习.当然,教师在这个过程中扮演着重要的角色,不单只是讲解问题,还要引导学生自己去发现问题,解决问题,使学生在整个学习过程中充分发挥主动性,自觉地联系所学知识,经常总结,并愿意学好这门课程.
[1]程其襄,张奠宙,魏国强,胡善文,王漱石.实变函数与泛函分析基础[M].3版.北京∶高等教育出版社,2010.
[2]周明强.实变函数伦[M].北京∶北京大学出版社,2001.
