复杂网络中集聚系数对链路预测算法的影响

黄子轩 马 超 徐瑾辉 黄江楠

（广东外语外贸大学 思科信息学院，广东 广州 510006）

0 引言

对于大规模的复杂网络，受时间、空间和实验条件的限制，我们能探测到的节点间的链接是有限的，大量链接的实验探测是困难的甚至是不可能的。因此如何根据已知的网络数据信息，通过设计合适的预测算法，预测节点间未知链接存在连边的可能性，是当前复杂网络科学研究的重要课题之一，此即所谓的链路预测问题。实际上，链路预测问题作为数据挖掘领域的一个子问题，在信息科学领域早已展开了研究（如基于马尔科夫链和机器学习的方法[1]）。但在现代大规模复杂网络的框架下，传统的链路预测算法远不能满足人们对预测效率和预测精度的需求，因此有必要发展新的链路预测算法。

在链路预测算法研究中，由于节点的属性信息难以获取，所以基于局部信息的相似性指标的链路预测算法受到了更大的关注[2]。近年来，基于局部信息的相似性指标不再单一地考虑共同邻居的数量或其度值，研究者们开始把共同邻居之间的联系也加以考虑[3]。但并不是所有的网络都需要考虑共同邻居的相互关系，甚至有时候会降低其准确率。

如今多数工作都是针对新的链路预测算法的提出，较少工作揭示出研究不同的网络结构与算法选择之间的关系。本文基于真实网络和模拟网络上的实验，对网络的节点集聚系数、边集聚系数与链路预测算法之间的关系进行分析，并研究何时需要考虑共同邻居之间的相互关系[4]。

1 问题描述

定义G(V,E)为一个无向网络，其中V为节点集合，E为边集合。网络的总节点数为N，边数为M。该网络共有N(N-1)/2个节点对，即全集U。这样，链路预测问题可描述为：构建某种相似度指标，对没有连边的节点对(x,y)计算其相似度Sxy，Sxy越大，节点对(x,y)出现连边的概率越大。

为了衡量算法的精确度，我们将已知连边E分为训练集ET和测试集EP两部分，其中EP为在E中随机抽取的10%的边，剩下的边均匀分配至ET。 另外，将属于U但不属于E的边定义为不存在的边。本文使用AUC指标来衡量算法的准确性。AUC(area under the receiver operating characteristic curve)定义为随机在测试集中选取的边的分数值比随机选择的一条不存在的边的分数值高的概率。即每次随机从测试集中选取一条边与随机选择的一条不存在的边进行比较，加分规则如下：若测试集的边的分数值大于不存在的边的分数值，则加1分；若两个分数值相等，则加0.5分；若测试集的边的分数值小于不存在的边的分数值，则加0分。重复以上步骤，独立地比较n次，定义n1为测试集中边的分数值大于不存在的边的分数值的次数，定义n2为两个分数值相等的次数，则定义AUC为

节点集聚系数用来描述一个节点的邻接点之间相互连接的程度，将该系数运用在社交网络中，其意义为该用户的朋友之间也是朋友的概率。设网络中一个节点为vi，该节点的集聚系数C(i)等于其邻接点之间连边的数量除以邻接点之间可以连出的最大边数。设ei为节点vi的邻接点之间连边的数量，k(i)为节点vi的度值，则

边集聚系数：在一个无向网络G(V,E)中，设一条边为E(u,v)，其端点分别为u和v，考虑u和v有多少个共同邻居w，即存在另外两条边E(u,w)，E(v,w)与E(u,v)形成闭合三角形。所以，将E(u,v)的边聚集系数ECC(u,v)定义为包含该边的三角形与该边最多可能构成的三角形个数之比，即：

边集聚系数刻画了两个节点之间联系的紧密程度，而聚集效应是复杂网络中的一个重要性质。网络的平均边集聚系数刻画出网络整体的紧密程度，因此，本文认为网络的平均边集聚系数能较好地区分出不同结构的网络[5]。本文涉及到以下8种相似性指标：

CN指标：该指标定义为两个节点的共同邻居数量。对于节点i，定义i的邻居集合为Г(i)，设节点x和y节点的相似性为Sxy，即Sxy=

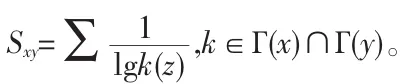
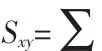
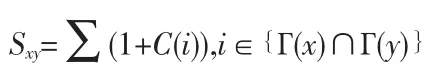
CAR指标[7]：该指标以CN指标为基础，加以考虑共同邻居间的相互关系，定义如下：

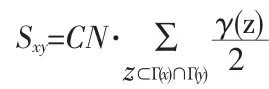
其中，γ(z)为节点z与两端节点以及其余共同邻居之间的连接数。CAA指标：该指标以AA指标为基础，加以考虑共同邻居之间的相互关系，定义如下：

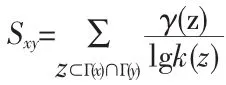
CRA指标：该指标以RA指标为基础，加以考虑共同邻居之间的相互关系，定义如下：

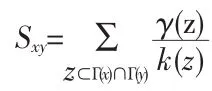
CCC指标：该指标以CC指标为基础，加以考虑共同邻居之间的相互关系，定义如下：

3 模拟网络实验

3.1 数据集

复杂网络普遍存在于真实社会中，为了充分考虑不同类型的网络，本文首先通过pajek生成的小世界网络进行模拟。其中，本文通过软件生成的小世界网络的设置均为200个节点，节点平均度分别为20和30。表1为节点平均度为20的小世界网络的拓扑信息和实验结果，表2为节点平均度为30的小世界网络的拓扑信息和实验结果。将上述8种算法在小世界网络中进行实验，并比较准确率。在AUC测试正确率中，对原始数据集进行了随机抽取分成了训练集（含90%的连边数）和测试集（含10%的连边数）两部分，随后进行了105次的随机抽样比较。

3.2 实验结果

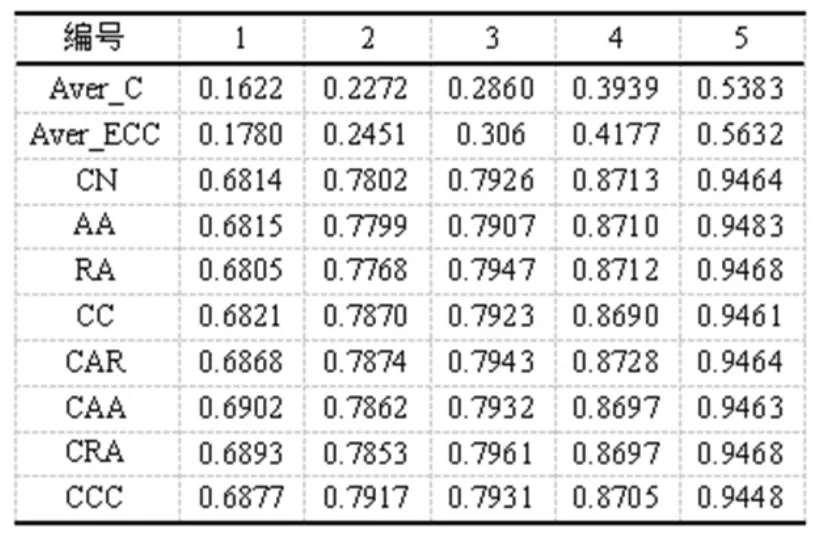
表1 小世界网络（K=20）的拓扑信息和实验结果

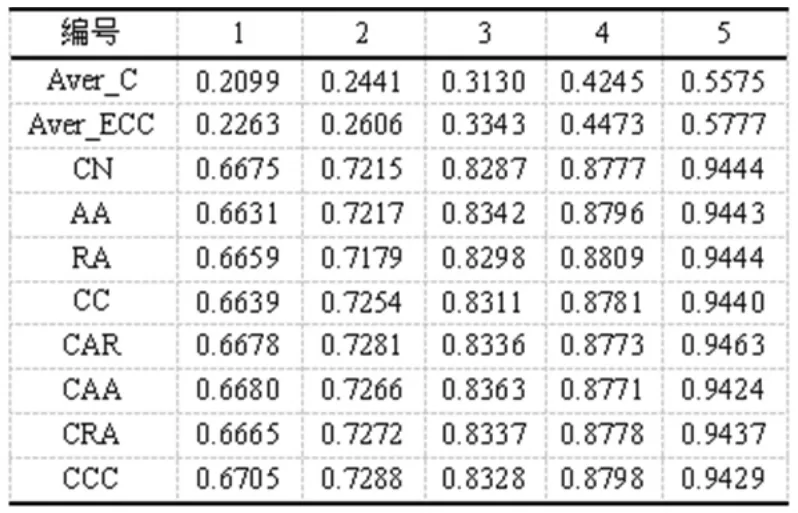
表2 小世界网络（K=30）的拓扑信息和实验结果

3.3 实验分析

由表1和表2可以看出，随着网络的平均节点集聚系数的增大，网络的平均边集聚系数也在增大，各个链路预测算法的准确性也在提高。小世界网络的平均节点集聚系数与平均边集聚系数较为接近。在小世界网络中，当网络的平均节点集聚系数较为低的时候，这四种改进后的算法比原算法有更好的表现，但随着网络的平均节点集聚系数的提高，突出程度则在降低。因此，本文认为对于有较低的平均节点集聚系数的网络，考虑共同邻居之间的相互关系能更好地表现出节点之间的连接紧密性。对于高平均节点集聚系数的网络，因其网络本身拥有较好的紧密性，再加以考虑共同邻居之间的相互关系对于提高算法有效性的用处不大。

4 真实网络实验

4.1 数据集

本文使用了4个真实网络：adjnoun网络、football网络、polbooks网络、US power grid网络进行实验，对上一小节实验分析进行验证。这里，我们仍采用上述8种算法在各个网络中进行实验，并比较准确率。在AUC测试正确率中，对原始数据集进行了随机抽取分成了训练集（含90%的连边数）和测试集（含10%的连边数）两部分，随后进行了105次的随机抽样比较，表3为4个真实网络的实验结果。

4.2 实验结果

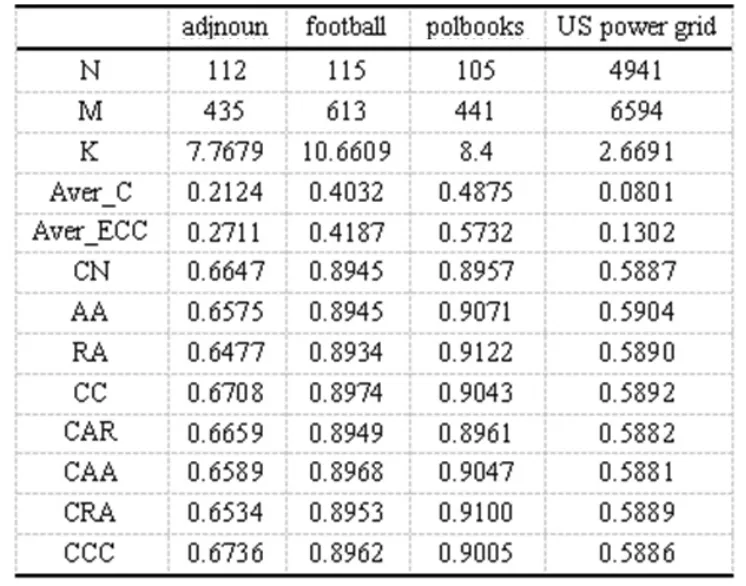
表3 4个真实网络的拓扑信息和实验结果

4.3 实验分析

通过表3，我们发现football网络和polbooks网络拥有较高的平均节点集聚系数，8种链路预测算法在这两个网络中表现出约为90%的正确率。而US power grid网络的平均节点集聚系数极低，因此链路预测算法在该网络上表现均不佳，不到60%的正确率。adjnoun网络相对于football网络和polbooks网络拥有较低的平均节点集聚系数，且两种平均集聚系数较为接近，相对于US power grid网络更接近小世界网络的特性，而4种改良算法的正确率对比原算法的正确率有一定的提高，反观US power grid网络的实验中，改良算法与原算法几乎无异。整体来说，在真实网络上的实验结果符合第三部分的实验分析。

5 总结

在复杂网络的链路预测研究中，以前的工作主要集中提出新的链路预测算法。不同于此，为了更好地理解算法与网络之间的联系，本文以集聚系数为切入点，研究了其对链路预测算法的影响，加深理解影响算法准确性的因素，以及算法的适用范围。本文工作综合考虑了网络结构的多样性以及算法的适用性，对链路预测算法与网络结构之间的联系进行深入的研究。实验表明：模拟实验的结论同样适用于真实网络，对于链路预测的研究有重要的参考价值。

［1］Sarukkai RR.Link prediction and path analysis using Markov chains[J].Computer Networks,33(1-6)∶377－386,2000.

［2］吕琳媛，陆君安，张子柯，闫小勇，吴晔，史定华，周海平，方锦清，周涛.复杂网络观察[J].复杂系统与复杂性科学,2010,7（2-3）：173-186.

［3］东昱晓，柯庆，吴斌.基于节点相似性的链接预测[J].计算机科学,2011，38(7)：162-164.

［4］Feng X,Zhao JC,Xu K.Link prediction in complex networks∶a clustering perspective[J].European Physical Journal B,2012,85∶3.

［5］李敏，张含会，费耀平.融合PPI和基因表达数据的关键蛋白质识别方法[J].中南大学学报：自然科学版，2013,44(3)：1024-1029.

［6］Zhou T,Lü L,Zhang Y-C.Predicting missing links via local information[J].European Physical Journal B,2009,71∶623-630.

［7］Cannistraci CV,Alanis-Lobato G,Ravasi T.From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks[J].Scientific Reports,2013,3∶1613.