基于通径分析与可拓学的公路泥石流危险性评价

王英杰，王 磊，荣起国，武永辉

（1.吉林大学建设工程学院，长春130026；2.北京大学工学院，北京100871；3.武警工程大学基础部，西安710086）

0 引 言

流泥石流危险性评价已经成为当前国内外灾害科学研究的热点之一，也是泥石流预测预报和防灾减灾的重要内容。国外对泥石流危险性评价始于20世纪70年代末期，日本在1977年首次对泥石流危险性开展了研究［1］；国内在20世纪80年代末，刘希林和唐川［2］提出了一系列泥石流危险性判定的方法，到90年代初，各种数学模型如线性回归、层次分析法、灰色理论、遗传神经网络、模糊数学等方法开始在这一研究中得以广泛应用和发展［3－7］。

泥石流危险性是根据泥石流危险因子评价的，刘希林采用“灰色系统理论”中的灰色统计方法，根据专家通信调查总结出2项主要危险因子以及8项次要危险因子，并得到广泛应用。目前这些广泛应用的评价方法简单易行，但多是将刘希林提出的10个评价因子直接或者经过简单转换之后代入相应的公式得到泥石流危险度，未能充分考虑各评价因子与危险度的相关性，并且在某些情况下，获取以上全部评价指标是较为困难的，因此需要对以上指标进行筛选，以实现利用较少的指标进行危险性评价的目的，通径分析方法则能较好地解决上述问题，考虑了各影响因子与危险度之间的相关性，根据相关程度的强弱对其进行筛选，使得根据较少的评价因子实现危险性评价成为可能。

本文以大西沟泥石流为例，利用通径分析方法，对以上因子进行进一步的筛选，选择了与危险度相关程度较强的7个评价因子，并利用筛选后的评价因子以可拓学理论为基础确定泥石流危险性等级，为在仅有少量评价指标或不易获得泥石流全部基本特征指标的情况下进行泥石流危险性评价提供了一种新的思路，同时为利用通径分析与可拓理论进行泥石流危险性评价提供了参考。

1 通径分析

通径分析是美国数量遗传学家Sewall Wright于1921年提出来的一种多元统计技术，它是简单相关分析的继续，在多元回归的基础上将相关系数加以分解，通过直接通径、间接通径及总通径系数分别表示某一变量对因变量的直接作用效果、通过其他变量对因变量的间接作用效果和综合作用效果［2，8，9］。

对于一般的多元线性回归分析，设有自变量X1，X2，…，Xk和因变量Y，

将式（1）与式（2）相减得：

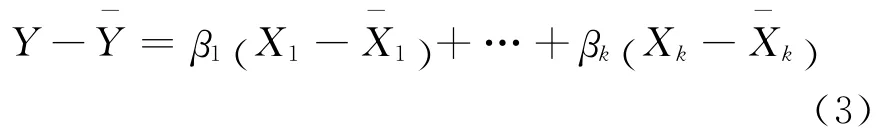
式（3）两边同时除以被解释变量Y的标准差σy得：

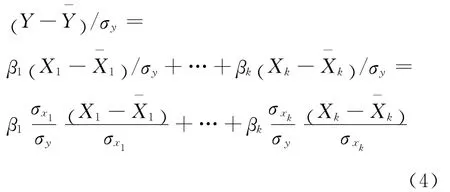
利用最小二乘法求出式（4）各自变量线性回归系数的求解模型，在此基础上，进行一定的数量变换，则可得出如下各简单相关系数的分解方程：

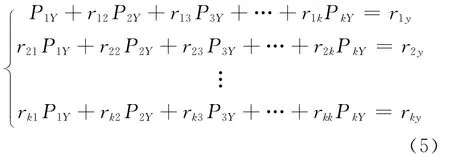
以上为通径分析的基本模型，每一个自变量与因变量之间的简单相关系数可被分解为直接通径效果部分和间接通径效果部分，其中rij为各自变量的简单相关系数，riy为自变量与因变量之间的简单相关系数，PiY为直接通径，表示Xi对Y的直接影响效应，rijPjY为间接通径，表示Xi通过Xj对因变量Y的间接影响效应。

2 评价因子的确定

笔者以大西沟地区30条泥石流沟的实际调查资料为基础，对刘希林模型所提出的流域面积X1、主沟长度X2、流域最大相对高差X3、流域切割密度X4、主沟床弯曲系数X5、泥沙补给段长度比X6、24 h最大降雨量X7和流域内人口密度X8等8项次要危险因子以及一次泥石流最大冲出量X9、泥石流发生频率X102个主要危险因子进行通径分析。

将利用刘希林模型计算出的泥石流危险度作为因变量Y，某地区30条泥石流沟的基本参数与危险度见表1。利用SPSS16.0软件进行分析计算，得到各变量与因变量之间的相关系数，见表2。

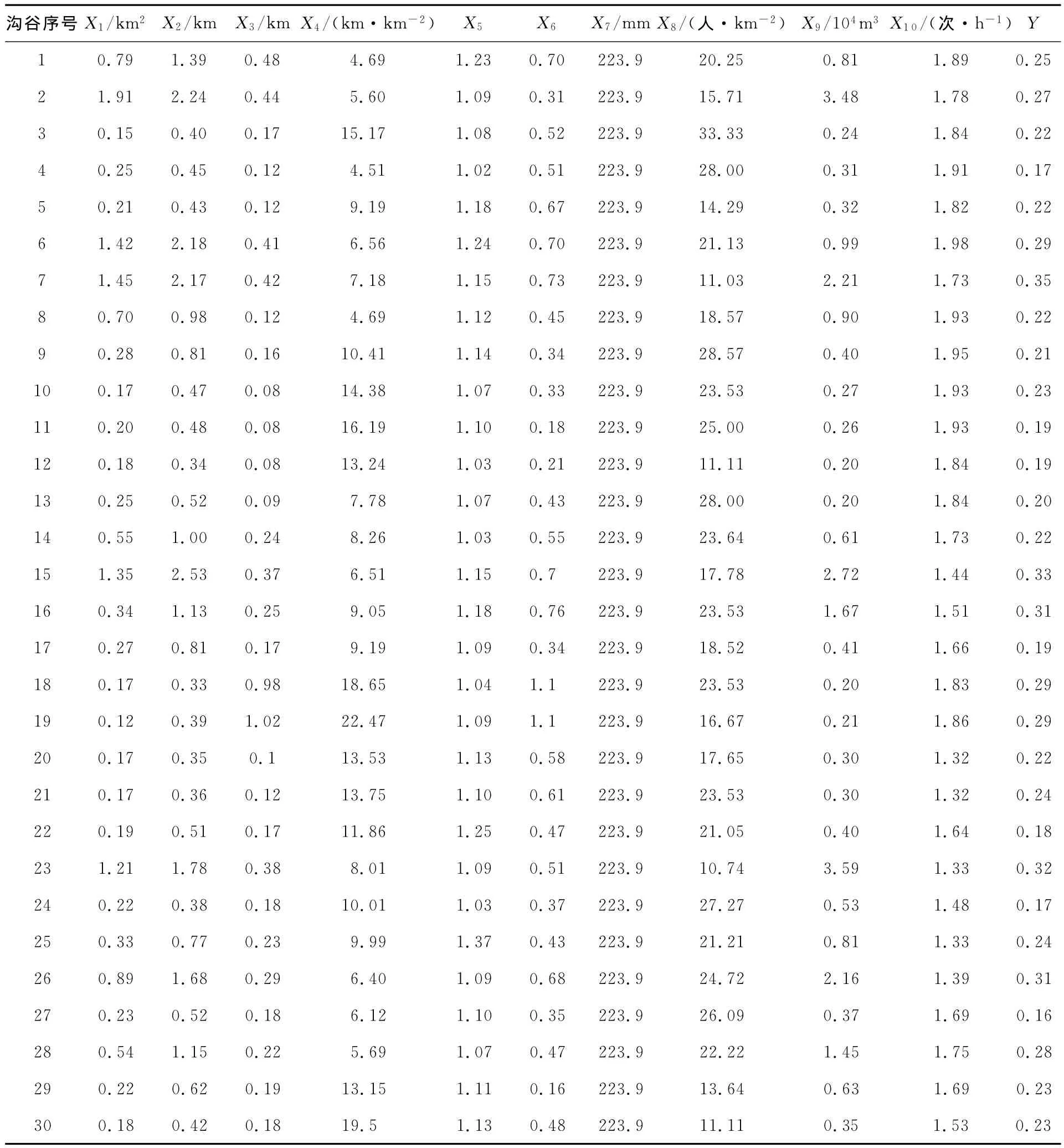
表1 某地区30条泥石流沟各基本参数及危险度Table 1 Basic parameters and danger degrees of 30 debris flow gullies

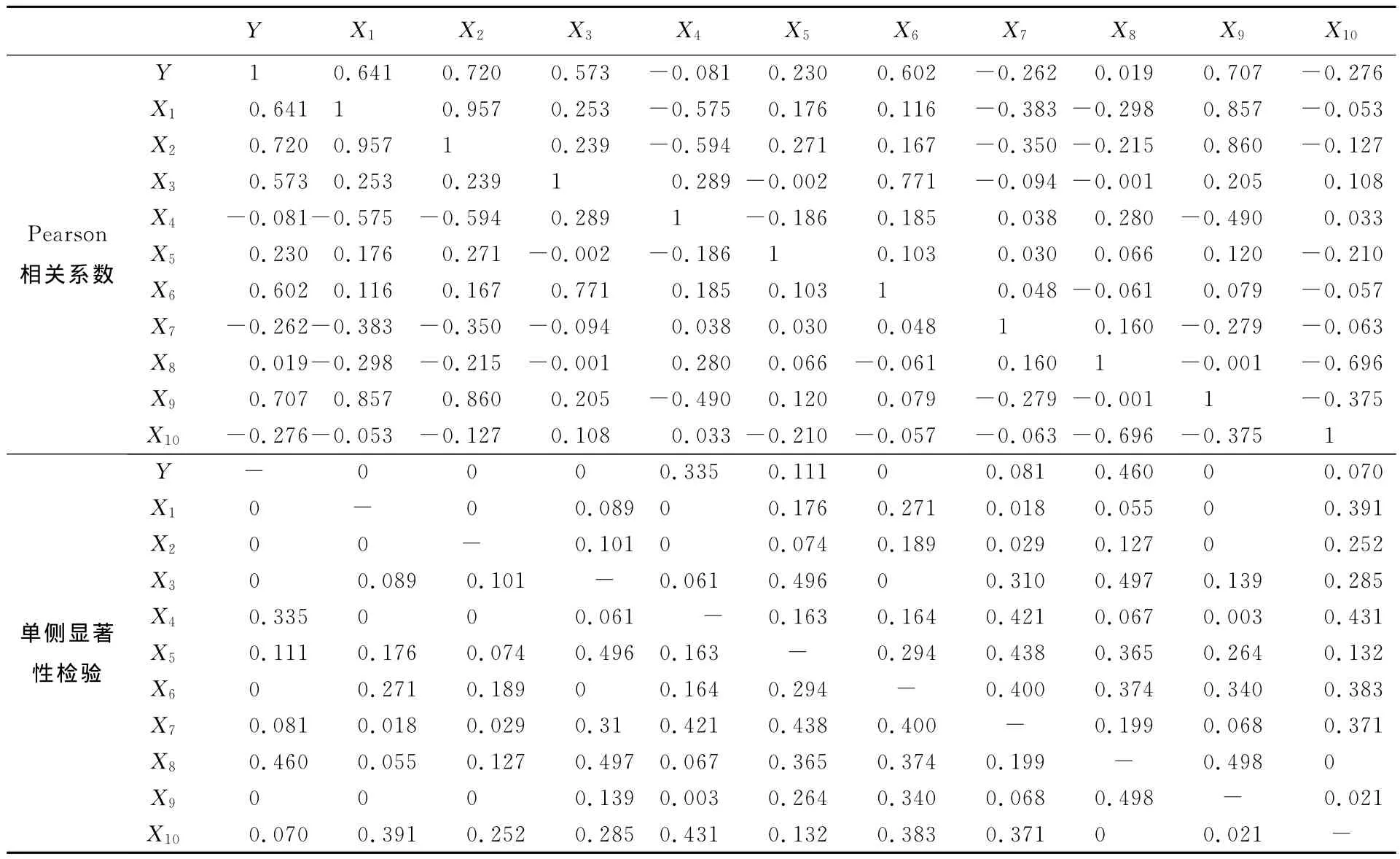
表2 相关系数及检验输出结果Table 2 Pearson correlation coefficient and significant test results

由表2中的计算结果可知，10个评价因子中对泥石流危险度影响最主要的几项从大到小分别是X2（主沟长度）、X9（一次泥石流最大冲出量）、X1（流域面积）、X6（泥沙补给段长度比）、X3（流域最大相对高差）、X5（主沟床弯曲系数），其简单相关系数分别达到0.720、0.707、0.641、0.602、0.573、0.230，相对而言，其他因子对其影响较小，如人口密度与危险度的简单相关系数仅为0.019，远不及上述几项因子。此外，24 h最大降雨量是诱发泥石流暴发的一个不可忽略的重要因素，但由于上文中作为基础数据的30条泥石流沟处于相近的区域范围内，其降雨量取值相同，因此导致在上述计算分析过程中并未体现出24 h最大降雨量对泥石流危险度的影响，所以在进行危险性评价时，可以主要依据于上述分析筛选出的6项因子，同时考虑24 h最大降雨量这一因子，使得在保证评价结果正确性的前提下，以减少评价因子的数量，简化评价过程。

3 危险性评价

在以上确定的评价因子的基础上，利用可拓学方法对其进行危险性评价［10－12］。

首先确定经典域：

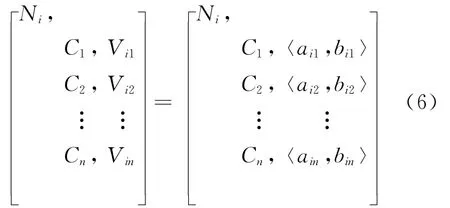
式中：R0i为一个物元；Ni为第i个评价类别；Ci为第i个评价指标；Vi为Ci所规定的取值范围，即经典域，Vij＝〈aij，bij〉，（i＝1，2，…，n；j＝1，2，…，m）。

由集合P、它的n个特征Ci以及将标准量值范围加以拓展了的取值范围Vpi＝〈api，bpi〉组成的物元称为节域物元，可表示为：

式中：P为评价类别的全体；Vpi为P关于Ci的取值范围，即P的节域。

对于待判别的泥石流沟，将调查结果用物元表示，称为泥石流危险性评价的待评物元，表示为：

根据可拓集合的关联函数［13］，可得到待评泥石流沟物元关于各类等级的关联度，第i条泥石流沟的第j个因子危险性类别的关联度为：

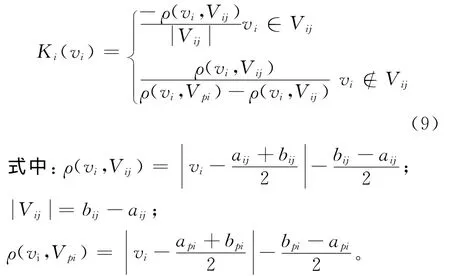
泥石流沟p关于评价类别t的关联度为：

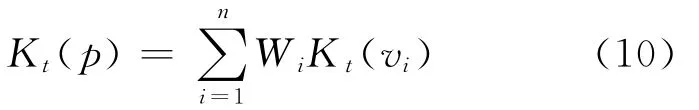
式中：Wi为各评价指标的权系数，可通过专家打分法、简单关联函数法、按评价因子的灰关联排序等方法来确定［2，11，1］。若Kt0（p）＝max Kt（p），则评定p属于等级t0。

4 泥石流危险性评价举例

4.1 泥石流沟基本特征

大西沟泥石流流域面积大约为0.67 km2，高程1030～1300 m，泥石流主沟曲线长度1.37 km，直线长度为1.16 km，泥沙补给段长度比大约为51%，一次最大冲出量大约为1.93×104m3，当地24 h最大降雨量为217 mm。该泥石流沟的三维立体图见图1。

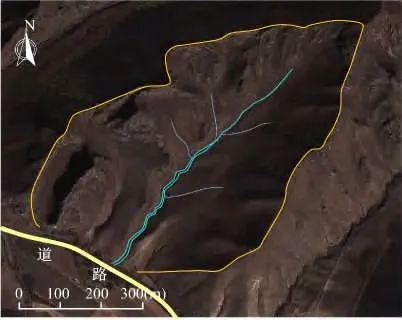
图1 泥石流沟三维立体图Fig.1 Three-dimensional topography of the debris flow valley

4.2 泥石流危险性评价

根据之前的通径分析，此处选取X1、X2、X3、X4、X5、X6和X7共7个代表性评价因子进行危险性评价。各评价因子的取值：X1＝0.67 km2；X2＝1.37 km；X3＝270 m；X4＝1.18；X5＝51%；X6＝1.93×104m3；X7＝217 mm。并且根据各评价因子的取值范围对其进行分级，结果见表3。

通过对评价因子进行无量纲化，构造物元，得到各泥石流危险性评价因子的权重：X1为0.1860，X2为0.1395，X3为0.1163，X4为0.0233，X5为0.0930，X6为0.3722，X7为0.0698［1］。

表3 泥石流危险性等级划分Table 3 Classification of debris flow hazard

然后利用公式（9）与公式（10）可得到泥石流沟关于四类危险性级别的关联度分别为K1（p）＝－0.2889，K2（p）＝0.0344，K3（p）＝－0. 6265，K4（p）＝－0.7504，可据此判断该泥石流沟危险性等级属于中度危险。

5 结束语

本文通径分析结果显示，在目前泥石流危险性评价时常用的10个因子中，主沟长度、一次泥石流最大冲出量、流域面积、泥沙补给段长度比、流域内最大相对高差、主沟床弯曲系数其简单相关系数分别达到0.720、0.707、0.641、0.602、0.573、0.230，同时由于24 h最大降雨量对泥石流的启动具有至关重要的作用，因此本文最终选取以上7个因子并利用可拓学方法进行泥石流危险性评价，评价方法和结果都具有较好的可信度。

与其他评价模型相比，本文中评价因子的筛选过程考虑了各项因子与泥石流危险度相关程度的强弱，使得评价结果更加合理可信，同时减少了评价因子的数量，特别是减少了泥石流发生频率这类不易获取的因子，使得泥石流危险性评价更加简化易行。在对各项因子进行筛选后将可拓学方法应用到泥石流危险性评价中，评价过程合理，能较真实地反映实际泥石流的危险等级，可为类似工程的危险性评价提供可行的思路。

［1］足立胜治，德山九仁夫，中筋章人.土石流发生危险度の判定にフやて［J］.新砂防，1977，30（3）：7-16.

Adachi Masao，Sankyu Katsuji，Virtue Akihito.The like risk decision in your current residence［J］New Sand Control，1977，30（3）：7-16.

［2］刘希林，唐川.泥石流危险性评价［M］.北京：科学出版社，2004.

［3］夏添.震区泥石流危险性评价及预警减灾系统研究［D］.成都：成都理工大学，2013.

Xia Tian.Research of debris flow risk assessment and early warning and mitigation system［D］. Chengdu：Chengdu University of Technology，2013.

［4］郭继发，崔铁军，崔伟宏，等.适宜尺度区间上的多尺度区域泥石流危险性评价［J］.吉林大学学报：地球科学版，2012，42（1）：150-160.

Guo Ji-fa，Cui Tie-jun，Cui Wei-hong，et al.Multi scale regional debris flow hazard assessment on fitting scale interval［J］.Journal of Jilin University（Earth Science Edition），2012，42（1）：150-160.

［5］谷光复，王清，张晨.基于投影寻踪与可拓学方法的泥石流危险度评价［J］.吉林大学学报：地球科学版，2010，13（2）：17-19.

Gu Guang-fu，Wang Qing，Zhang Chen.Extenics method based on projection pursuit to debris flow risk assessment［J］.Journal of Jilin University（Earth Science Edition），2010，13（2）：17-19.

［6］罗骑龙.基RS和GIS龚嘴电站库区地质灾害危险性评价［D］.成都：成都理工大学，2011.

Luo Qi-long.The RS and GIS Gong Mouth Power Station reservoir geologic disaster danger evaluation［D］.Chengdu：Chengdu University of Technology，2011.

［7］杜家菊，陈志伟.使用SPSS线性回归实现通径分析的方法［J］.生物学通报，2010，45（2）：4-6.

Du Jia-ju，Chen Zhi-wei.Use SPSS Linear regression to realize size analysis［J］.Journal of Biology，2010，（2）：4-6.

［8］敬艳辉，邢留伟.通径分析及其应用［J］.统计教育，2006（2）：24-26.

Jing Yan-hui，Xing Liu-wei.Size analysis and its application［J］.Journal of Statistics Education，2006（2）：24-26.

［9］何隆祥，王清，熊辉，等.膨胀土边坡稳定影响因素敏感度的通径分析［C］∥第九届全国工程地质大会论文集.青岛：中国地质学会工程地质专业委员会，2012：186-191.

［10］赖海林，孟庆辉，敖翔.可拓方法在泥石流危险性评价中的应用［J］.路基工程，2009（2）：157-158.

Lai Hai-lin Meng Qing-hui，Ao Xiang.Extension method in the application of the debris flow risk assessment［J］.The Subgrade Engineering，2009（2）：157-158.

［11］张艳，钟诗胜，李江.实例推理的可拓方法及其应用［J］.吉林大学学报：工学版，2009，39（2）：424-429.

Zhang Yan，Zhong Shi-sheng，Li Jiang.Extension methods in case-based reasoning and applications［J］.Journal of Jilin University（Engineering and Technology Edition），2009，39（2）：424-429.

［12］申桂香，邵娜，张英芝，等.基于可拓理论的数控机床顾客满意度评价［J］.吉林大学学报：工学版，2011，41（S1）：164-167.

［13］刘沐宇，李新平.可拓识别方法在巷道围岩分类中的应用［J］.岩石力学与工程学报，1999，18（增刊）：1295-1297.

Liu Mu-yu，Li Xin-ping.Extension identification method in the application of classification of surrounding rock of roadway［J］.Journal of Rock Mechanics and Engineering，1999，18（Sup.）：1295-1297.