宽边界区域和简单区域间拓扑关系的表示及推理

李 健，欧阳继红，朱佳斌，廖梦兰，赵 慧

（1.吉林农业大学信息技术学院，长春130118；2.吉林大学计算机科学与技术学院，长春130012；3.吉林大学教育部符号计算与知识工程重点实验室，长春130012；4.浙江工业大学 计算机科学与技术学院，杭州310014；5.吉林大学数学研究所，长春130012）

有关空间推理［1］的基本模型主要有4－交模型［2］、区域间拓扑关系的层次表达法［3］等和区域连接演算（Region connection calculus，RCC）模型［4］。这些模型主要是用来描述简单对象间的拓扑关系的，对于同时结合宽边界区域［5］和简单区域之间的拓扑关系很少涉及，因此其表达能力相对有限，一定程度上制约了空间推理在其相关学科的应用及发展。

本文为了对宽边界区域和简单区域间的拓扑关系进行表示和推理，基于RCC5得到了宽边界区域和简单区域间的交集模型，根据宽边界模型的约束条件提出算法，可以得到11种可以实现且完备的拓扑关系。进而可将本文所建立的宽边界区域和简单区域间拓扑关系的表示和推理模型，用于热带气旋路径预报中对于异常路径［6］的预报，可以表示和分析岛屿沿海地区受气旋影响的情况，进而完善岛屿沿海地区台风预警和灾害评估机制，对建立防灾预警机制、减小灾害损失和人员伤亡具有指导意义。

1 宽边界区域和简单区域间的交集模型

1.1 宽边界区域定义

宽边界区域［7］是一类对边界不敏感的模糊区域，可将其分为外部区域和内部区域，两者之差就是宽边界。因而，宽边界区域的边界具有一定的宽度和面积，如图1所示，其中X、Y均为简单区域，且X和Y间的拓扑关系为NTPP（X，Y），则定义Y0－X0为简单区域X的宽边界（其中X0，Y0分别表示X、Y的内部）。

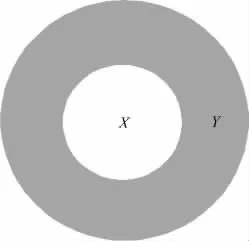
图1 宽边界区域Fig.1 The region with broad boundary

1.2 宽边界区域和简单区域间交集模型的建立

对于两个区域的情况：由于本文考查的是简单区域，所以上述表示的含义是把R2－｛∂A∪∂B｝划分成4个部分，如图2所示。

图2 两个区域的划分Fig.2 Partition of two simple regions

A0∩B0，A0∩（B1）0，（A1）0∩B0，（A1）0∩（B1）0这4个开集两两不相交，从而由此推出两个区域拓扑关系互斥且完备，其中实际存在的情况恰好满足RCC5关系［8－9］。基于该思想，可以先对一个宽边界区域和一个简单区域间的拓扑关系进行研究，将R2－｛∂A∪∂B∪∂C｝划分成8个子部分，如图3所示。

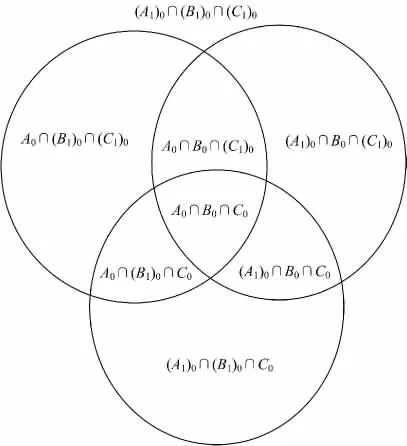
图3 三个区域的划分Fig.3 Partition of three simple regions

根据划分出的8个子部分（B是A的洞），可以建立相应的8-交集矩阵模型［10］：

式中：A0表示A的内部；A1表示A的补集。

通过每个位置上集合的空与非空，确定2×2 ×2的0-1矩阵，用来描述3个区域间的拓扑关系。

该模型加入适当的约束条件后可以表示一个宽边界区域和一个简单区域间的交集矩阵，即可作为宽边界区域和简单区域间的交集模型。

1.3 宽边界区域和简单区域拓扑关系约束条件

理论上有28个一个宽边界区域和一个简单区域间的交集矩阵，但是并不是所有的矩阵都是可以实现的。通过加入约束条件，除去矩阵模型中不可实现的情形，得到所有可实现的一个宽边界区域和一个简单区域间的交集模型。

约束条件1 一个0-1矩阵与一个可以实现的三元拓扑关系相对应，必须满足：

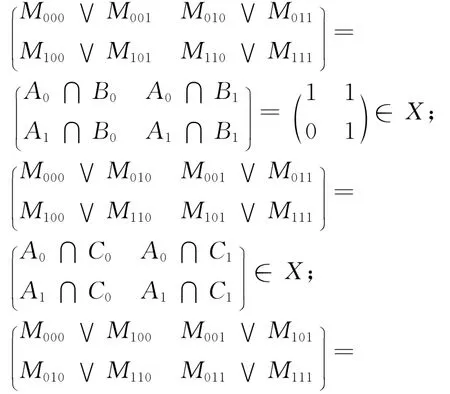
约束条件2 因为考虑的是简单有界区域，则有：（A1）0∩（B1）0∩（C1）0非空，即M111＝1。

约束条件3 宽边界区域的边界必须具有一定的宽度，因此宽边界外部区域A和内部区域B之间必须满足A真包含B。

1.4 宽边界区域和简单区域的拓扑关系算法

算法的基本思想是：①每个0-1矩阵以二进制数（用含有8个元素的0-1数组表示）的形式给出，首先生成理论上的256种0-1矩阵，即把0～255内的所有整数i转化为0-1矩阵；②依次扫描每个i转化的0-1数组，标记出所有满足约束条件的数组；③将所有满足条件的数组i保存到矩阵M中，并输出，其结果即为所求。

根据算法，最后得到11种满足一个宽边界区域和一个简单区域间的拓扑关系。图4中阴影部分即是宽边界区域。

图4 11种拓扑关系及其示意图Fig.4 11 kinds of topological relations

2 拓扑关系推理

拓扑关系推理即区域间拓扑关系的推理，可由一组或多组拓扑关系推理得到其他拓扑关系。将上文得到的宽边界区域和简单区域间的11种拓扑关系图进行整理分析，可以制定出拓扑关系复合表，如表1所示。

表1 拓扑关系复合表Table 1 Topological relation reasoning table

表中的f（A，B）表示A与B间的拓扑关系；f（A，C）表示A与C间的拓扑关系；f（B，C）表示B与C间的拓扑关系；DR表示相离；PO表示相交；PP表示被包含；EQ表示相等；PPI表示被插入到；由于f（A，B）＝PPI已经给定，可以根据f（A，C）或f（B，C）实现对应的推理和表示。

3 相关应用

随着对海洋和陆地空间利用需求的不断增大，岛屿的旅游价值、资源潜力和军事意义逐渐凸显。高度准确的气象预报尤其是准确的大风预报作为岛屿必需的服务项目，对日常生产生活有着重要指导作用，因此为岛屿地区制定完备的抗台风预案十分重要。

在具体的拓扑关系模型建立中，岛屿地区可分为陆上区域和沿海区域，如图5所示。由于岛屿地区海上贸易频繁，海防、沿海旅游业、渔业和集装箱进出口等业务大多分布在沿海地区，因此本文着重以岛屿的沿海地区为对象，对其受台风影响的情形进行分析，如图6所示。

图5 岛屿区域例图Fig.5 Hainan Island

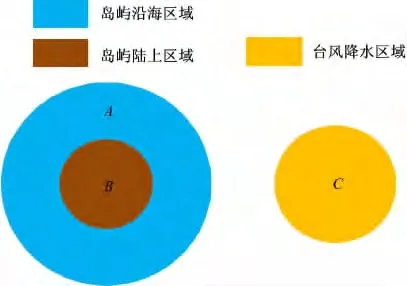
图6 台风强降水区域与岛屿沿海地区拓扑关系示意图Fig.6 Typhoon rainfall area with islands coastal areas of topological relations schematic diagram

值得注意的是，由于岛屿沿海有纵深且边界界定不明显，因此采用宽边界的模型。上述建立的台风降水与目标地区的拓扑关系模型是有具体实际意义并与上述所得的11种拓扑关系对应的。表2仅表示3例。

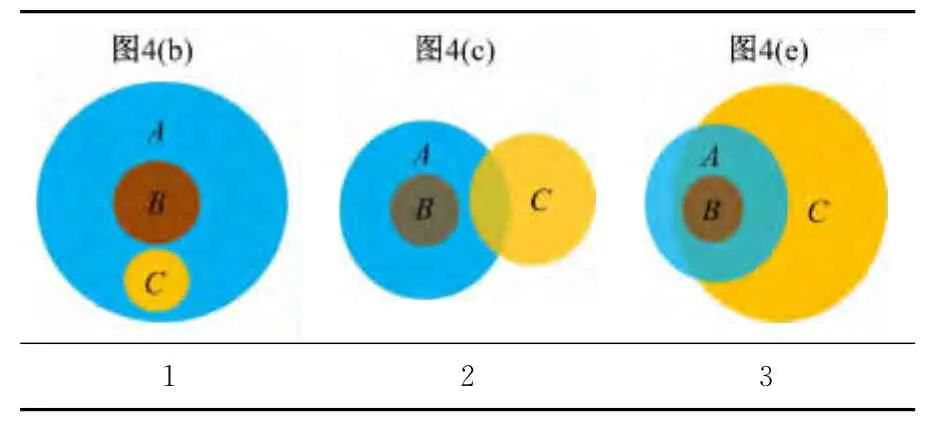
表2 拓扑关系对应Table 2 Topological relations corresponding diagram

表中序号2的说明：序号2所示的是岛屿沿海区域与台风强降水区域的降水影响拓扑关系模型，其拓扑关系具体包括PPI（A，B），PO（A，C），DR（B，C），它表示台风强降水区域C部分与岛屿陆上区域B相离，与岛屿的沿海区域A相交。即陆上地区B不会受到强降水的直接影响，但是沿海局部地区会因台风带来的降水而受灾害。于是，可启动对应级别的预案，通知海上船舶注意台风动向，适时停止海上作业，并提醒相关海域的过往船舶回港避风，保障沿海地区各项防御措施的实施，并密切关注气象部门发布的实时台风预报预警信息，以减轻灾害影响。

按照影响范围，台风对岛屿沿海区域的降水影响可分为：有局部影响、全境影响和无影响3种，即PPI（A，C）和EQ（A，C），DR（A，C）。根据上节建立的拓扑关系复合表（表1），可对岛屿沿海区域与台风强降水区域的降水影响进行全面推理。其中局部影响对应于图4中的拓扑关系图序号包括（b）（c）（e）（h）（j）（k）共6种，全局影响包括图序号（f）和（g）共2种，无影响的有（a）（d）（i）共3种。

4 结束语

建立了宽边界区域和简单区域间的交集模型，给出宽边界模型的约束条件并通过算法得到11种可实现的拓扑关系。在此基础上建立的台风－岛屿沿海地区降水拓扑关系模型可以备份目标地区可能发生的降水情形，为岛屿沿海地区抗台风工作提供了理论支持，有助于完善台风强降水预报和抗台风救灾机制。

［1］刘亚彬，刘大有.空间推理与地理信息系统综述［J］.软件学报，2000，11（12）：1598-1606.

Liu Ya-bin，Liu Da-you.A review on spatial reasoning and geographic information system［J］.Journal of Software，2000，11（12）：1598-1606.

［2］Egenhofer M J，Franzosa R D.Point-set topological spatial relation［J］.International Journal of Geographical Information System，1991，5（2）：161-174.

［3］邓敏，冯学智，刘文宝，等.地理信息系统中拓扑关系不确定性推理的方法［J］.模式识别与人工智能，2004，17（3）：326-331.

Deng Min，Feng Xue-zhi，Liu Wen-bao，et al.Uncertain reasoning approach to topological relations under locational uncertainty in GIS［J］.Pattern Cognition and Artificial Intelligence，2004，17（3）：326-331.

［4］Clarke B L.A calculus of individuals based on connection［J］.Notre Dame Journal of Formal Logic，1981，22（3）：204-218.

［5］杜晓初，郭庆胜，丁虹.宽边界区域拓扑关系量化分析与抽象［J］.武汉大学学报：信息科学版，2004，29（11）：1021-1024.

Du Xiao-chu，Guo Qing-sheng，Ding Hong.Quantitative analysis and abstraction of topological relation between regions with broad boundaries［J］.Geomatics and Information Science of Wuhan University，2004，29（11）：1021-1024.

［6］曹楚，王忠东.台风Aere（2004）与超强台风Gloria（1963）路径分析［J］.广东气象，2011，33（3）：20-22，26.

Cao Chu，Wang Zhong-dong.The track analysis of typhoon“Aere”（2004）and super typhoon“Gloria”（1963）［J］.Guangdong Meteorology，2011，33（3）：20-22，26.

［7］Clementini E，Di Felice P.Analgebraicmodel for spatial objects with indeterminate boundaries［DB／OL］.［2012-06-30］.Geographic objects with indeterminate boundaries 1996.pdf.

［8］Randell D A，Cohn A G.Modelling topological and metrical properties of physical processes［C］∥Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning，Los Altos，California，USA，1989：357-368.

［9］Randell D，Cui Z，Cohn A.A spatial logic based on regions and connection［C］∥Proceedings of the Third International Conference on Principles of Knowledge Representation and Reasoning，Cambridge，Massachusetts，USA，1992：165-176.

［10］李健，欧阳继红，王振鑫，等.三个简单区域间的拓扑关系的表示模型［J］.吉林大学学报：工学版，2013，43（1）：117-122.

Li Jian，Ouyang Ji-hong，Wang Zhen-xin，et al. Representation model of topological relationship among three simple regions［J］.Journal of Jilin University（Engineering and Technology Edition），2013，43（1）：117-122.