圆柱形发电装置和立管式海洋平台位置的优化

仲 夏 包胜平

（武汉理工大学交通学院 武汉 430063）

0 引 言

海洋能是一种清洁的可再生能源，取之不尽用之不竭，资料表明，全球海洋能约500亿kW.采用新型圆柱形浪潮流发电装置能有效地将海洋能转换为电能，并将电能提供给立管式海洋平台，因此浪潮流发电装置与立管式海洋平台构成取能－换能－用能的统一系统.海洋平台下方共4根立管，呈正方形分布；海洋平台周边有4个圆柱形浪潮流发电装置，该发电装置不仅能为海洋平台提供电能，还能减小水流对海洋平台立管的冲击作用.

现在很多学者在研究单圆柱方面主要开展不同雷诺数的圆柱绕流情况，以及圆柱的涡激振动；但是对于圆柱绕流不仅有单圆柱情况，也有相同大小圆柱的相互干扰问题.本文围绕实际问题——立管式海洋平台垂向螺旋桨式浪潮流发电系统相对位置优化的简化模型展开研究，优化的目的主要是减少水流对海洋平台立管的冲击作用，而对圆柱形发电装置的受力不做研究，因为圆柱形发电装置即使不和立管作为一系统布置，也会受到同样的水流作用力.

1 新型圆柱形浪潮发电装置简介

本装置为圆柱形，见图1.当所在水域出现浪潮流时，圆柱空腔壁内水位上升，推动对称桨，使其产生周向诱导速度，从而进行旋转，将水的动能转变成对称桨的动能，进而带动链条式能量转换器相应的一条链条进行传动，最终使其相应的发电机进行发电；当浪潮流退去，圆柱空腔壁水位下降，推动对称桨，使其产生反向的周向诱导速度，从而进行反向旋转，将水的势能转变成对称桨的动能，进而带动链条式能量转换器另一链条进行传动，最终使另一发电机进行发电.

2 单个立管的圆柱绕流计算

首先对立管的简化模型——单圆柱进行绕流的二维流场模拟，取立管直径0.01m，采用FLUENT软件计算Re＝200（v＝0.020 08m／s）和Re＝10 000（v＝1m／s）时的单圆柱绕流，得出升力系数、阻力系数以及斯托罗哈数的变化规律，并将结果与已有文献结果对比，证明该计算方法的可靠性.

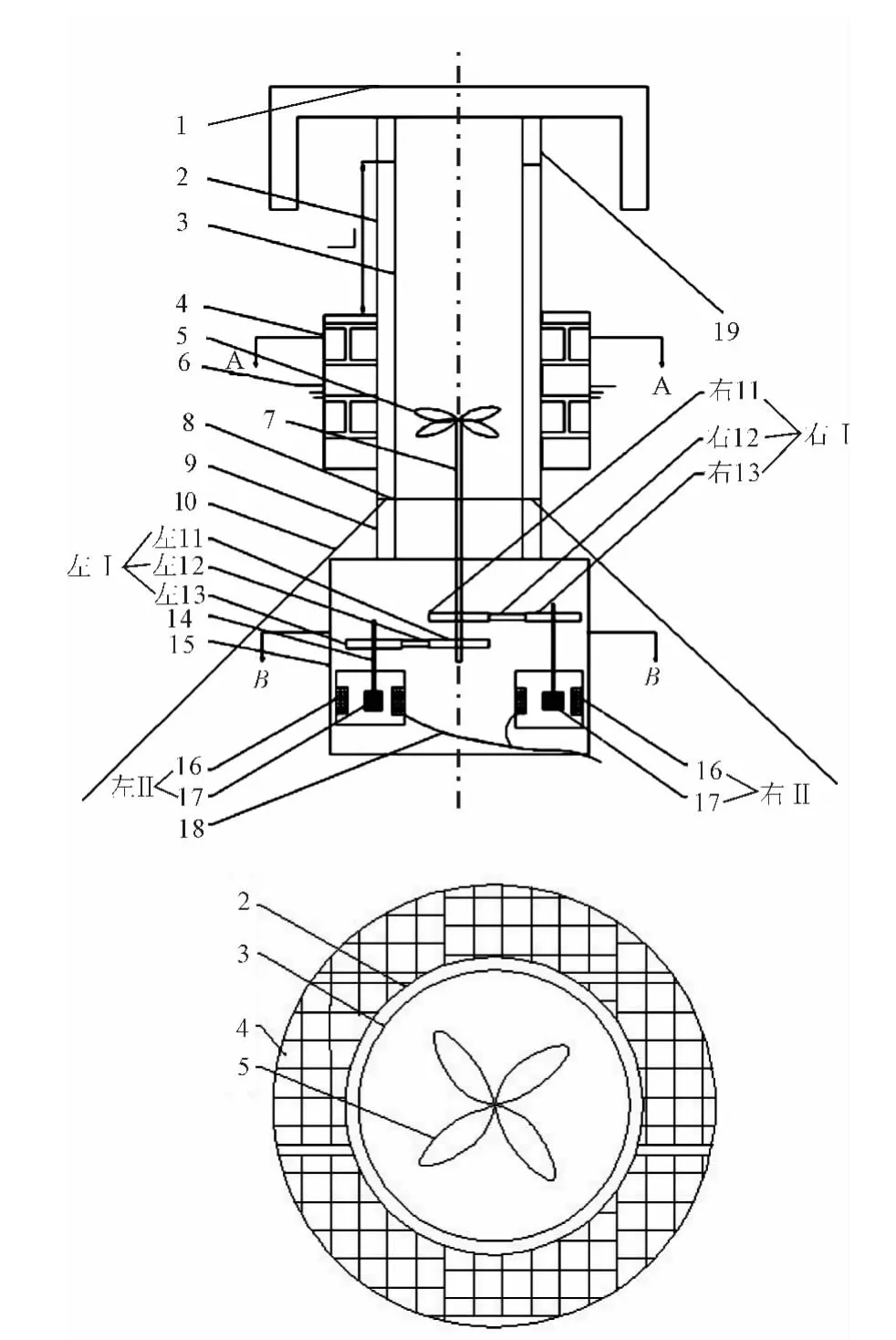
图1 新型圆柱形浪潮流发电装置侧视图

本文主要求解雷诺数Re＝1 0 0和1 0 0 0 0时的圆柱绕流情况，Re＝100时圆柱绕流为层流绕流，Re＝10 000时，虽然圆柱后部为湍流流动，但是圆柱表面仍为层流流动，故在分析静止圆柱本身受力时可以视为层流流动.

由连续性方程、动量方程可以得到描述二维不可压缩粘性流体的基本方程：纳维斯－斯托克斯方程（N－S方程）［1］

采用有限体积法对上述偏微分方程进行离散，然后用SIMPLE算法对离散方程进行求解，计算中时间推进采用一阶隐式格式，空间离散采用二阶迎风格式.观察结果所用参数采用如下.

式中：Sr为斯托罗哈数，取决于结构的形状断面；f为旋涡脱落频率；D为结构的特征尺寸（圆柱取直径D）；U为来流速度.

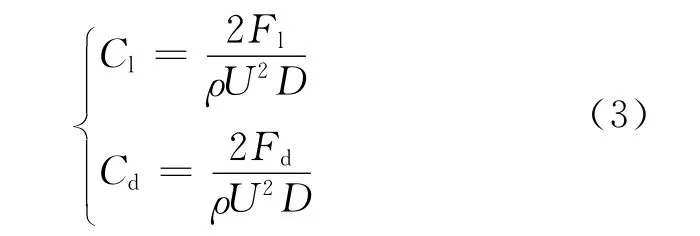
式中：Cl，Cd分别为升力系数、阻力系数；Fl，Fd分别为单位长度结构（圆柱）上的升力和阻力.

2.1 计算Re＝200的圆柱绕流

考虑到计算精度，取D＝0.01m的圆柱作为计算模型.流动介质为水，密度ρ＝998.2kg／m3，粘性系数μ＝0.001 003kg／（m·s），来流速度U∞＝0.020 08m／s，其雷诺数Re为200.

将流场计算域定为：单圆柱绕流选取流场大小为进口距圆柱中心0.125m，出口距圆柱中心0.375m，上下边界距圆柱中心各为0.125m，D＝0.01m.

采用Meshing软件划分流场网格，采用三角形网格，数值计算的边界条件：入口为速度入口，出口是outflow出口，顶部和底部边界为对称面边界条件，圆柱及阻隔板表面均为壁面无滑移条件，见图2.

图2 圆柱绕流流场的网格划分

网格画好后进入FLUENT计算，transient求解，采用laminar模式计算，时间步长设定为0.05s.所得结果见图3～4.

图3 Re＝200时的升力系数曲线

将计算所得结果和参考论文结果列于表1进行比较.

图4 Re＝200时的阻力系数曲线

表1 量纲－的量参数对比（Re＝200）

通过对比可得，FLUENT在Re＝200的计算情况下是比较可靠的.

2.2 计算Re＝10 000的圆柱绕流（v＝1m／s）

网格画好后进入FLUENT计算，transient求解，采用laminar模式计算（由于此雷诺数时圆柱处仍为层流泄涡），时间步长设定为0.005s，其他设置均同Re＝200的情况.

将计算所得结果和参考论文结果列于表2进行比较.

表2 量纲－的量参数对比（Re＝10 000）

通过2个雷诺数的计算，充分证明FLUENT计算圆柱绕流相关无因次参数的可靠性，圆柱上、下表面脱落的旋涡交错出现，然后进入尾迹，形成著名的“卡门涡街”.基于此，将FLUENT用于雷诺数为10 000时新型圆柱形浪潮发电装置和立管式海洋平台系统相对位置的优化.在一定程度上使立管受力最小，从而起到保护立管的作用，延长立管的使用时间.

3 系统位置优化

一般发电装置为多个，但取4个作为研究：（1）可以比较好的模拟实际；（2）将装置和立管式海洋平台呈中心对称布置，不用考虑浪潮的多向性和多变性，便于运算.

在此基础上有2种位置组合，如图5，图6.

图5 位置组合一

图6 位置组合二

如图5和图6所示，利用流场分析软件ANSYS对这2种系统组合中的立管进行受力分析，并依据所受阻力大小为位置优化依据，同时和没有发电装置的情况进行比较，计算技术路线为：ANSYS建模—网格划分—Fluent流场分析［8］.

3.1 ANSYS建模及网格划分

一般海洋平台立管直径为0.25m，相邻立管间的距离为10m，发电装置中心到4个立管中心的水平距离为13m，将现实条件简化进行模型的计算，参考文献［2］海洋平台立管模型直径为0.01m，相邻立管间的距离为0.4m，发电装置中心到四个立管中心的水平距离为0.52m，速度取为1m／s，雷诺数即为10 000.将这2种系统组合在ANSYS分别进行建模，考察在圆柱形发电装置的影响下立管所受阻力系数，并和无发电装置时的立管受力进行对比分析.

3.2 FLUENT流场及受力

［5］选择来流速度1m／s，进行立管在流场中的阻力系数的分析.

图7为无发电装置时立管阻力系数曲线图，此时4个立管阻力系数值分别为：0.31，0.36，0.31，0.35，总阻力系数为1.33.

图7 无发电装置时立管阻力系数曲线图

3.3 立管受力分析

现将3种情况的所受阻力系数列于表3进行对比（左上角为第1立管，右上角为第2立管，左下角为第3立管，右下角为第4立管.其他2种位置也按照此位置排列），见表3.

表3 三种情况的所受阻力系数对比

由表3可见：位置组合一立管所受阻力，小于无发电装置时立管所受的阻力，优化率η＝｜1.28－1.33｜／1.33＝3.8%，同时在最大值比较上也比无发电装置时较小（0.35＜0.36）；位置组合二立管所受阻力大于位置组合一立管所受阻力，相对无圆柱形发电装置时立管所受阻力稍小，优化率η＝｜1.31－1.33｜／1.33＝1.5%，所以这种情况虽然也有优化的效果，但是不明显.

4 结论与展望

1）通过采用FLUENT软件计算Re＝200和Re＝10 000时的单圆柱绕流，得出升力系数、阻力系数以及斯托罗哈数的变化规律，将所得结果与已有文献结果对比，证明了该计算方法在两者雷诺数情况下的可靠性.

2）对发电装置和海洋平台组成的系统位置进行分析，比较3种情况的阻力系数，得出：位置组合一为系统位置优选解，均小于无发电装置和位置组合二的立管所受阻力，优化率η＝｜1.28－1.33｜／1.33＝3.8%，能够在一定程度上起到减小立管所受阻力，有效减少水流对立管的冲击作用，保护立管，对生产实践有一定的指导意义.

3）综合3种情况，可以发现有圆柱形发电装置挡住立管时，立管的受力在不同程度上减小了，如果能够再将圆柱形发电装置在位置上进行合理的优化，最终可求得一个使立管的所受阻力在最大程度上减小的位置，得出位置最优解.

通过分析虽然得出了系统布置的优选解——位置组合一，但是这只是在角度上的优化，接下来还应该基于此在距离方面进行优化，最终确定优选距离，使立管所受阻力最小，从而最大可能地保护立管.

参考文献

［1］杨纪伟，滕丽娟，胥战海.多圆柱绕流旋涡脱落和流场形态概论［J］.人民长江，2009，40（3）：66－86.

［2］丁代伟.圆柱绕流及涡激振动的二维数值模拟［D］.天津：天津大学，2010.

［3］WU G X，HU Z Z.Numerical simulation of viscous flow around unrestrained cylinders［J］.Journal of Fluids and Structures，2006（22）：371–390.

［4］张群峰，何鸿涛，吕志咏.二维圆柱层流绕流及其控制数值模拟［J］.科学技术与工程，2009，9（5）：1187－1193

［5］詹 昊，李万平，方秦汉，等.不同雷诺数下圆柱绕流仿真计算［J］.武汉理工大学学报，2008，30（12）：129－132.

［6］杨 烁，吴宝山.二维圆柱绕流数值模拟［J］.中国造船.2007，48（增刊）：533－540

［7］陈 伟，宗 智.二维圆柱绕流的离散涡数值模拟［J］.舰船科学技术.2010，32（5）；111－115

［8］梁亮文.低雷诺数下圆柱横向受迫振荡和涡激运动的数值分析［D］.上海：上海交通大学，2009.