刚性开孔结构斜风向内压响应的风洞试验研究

余世策，李庆祥

（1.浙江大学 建筑工程学院，杭州 310058；2.广东省建筑科学研究院，广州 510500）

0 引 言

建筑结构的抗风设计是现代建筑设计的重要组成部分，随着人们对建筑安全性要求的不断提高，在重要工程的抗风设计中，经常会涉及建筑内部风荷载，尤其是对于大型厂房、机库等建筑，由于建筑开孔较大，势必导致建筑内部风荷载成为设计的重要考虑因素，因此仅采用外部风荷载的设计方法和理念已越来越不能适应当前建筑结构设计的发展要求。从近年来的发展趋势看，结构风致内压已然成为风工程研究的一个热点方向。

开孔结构风致内压响应特别是内压的脉动响应一直是困扰风工程界的一个重要问题，在理论方面，自Holmes第一个提出采用声学Helmholtz共振器来描述内压共振响应以来［1］，Liu＆Saathoff［2］、Vickery ＆Bloxham［3］、Sharma ＆ Richard［4－6］、Yu［7－8］、Guha［9］等一批学者对内压脉动机理及内压传递方程进行了深入探讨，Holmes＆Ginger［10］系统总结了内压脉动理论和预测方法，提出了完全无量刚化的内压传递方程；在实验方面，Liu＆Rhee［11］研究开孔大小和位置对内压共振响应的影响，Woods＆Blackmore［12］揭示了当房屋单面开孔和双面开孔以及孔口的大小及位置变化和风向角的变化对平均内压和峰值内压的影响，余世策等［13］对低层房屋模型进行了开孔状态下的多参数对比风洞试验，研究了开孔结构内部风压的空间分布特性、平均内压和脉动内压的特性，通过对风压系数时程的分析，探讨了内部风压峰值因子的取值规律及内外压的相关性特性。总体来讲尽管国内外诸多学者对内压响应进行了深入的研究，但仍有很多问题有待深入研究，特别是Sharma＆Richards［14］通过风洞试验研究了单一开孔建筑在斜向来流风作用下产生的Helmholtz共振效应，试验研究中发现相比正面来流风而言，斜向来流风所产生的Helmholtz共振效应导致内压产生更强烈的脉动，指出涡激振动是导致内压共振强度增大的重要原因，而Oh＆Kopp［15］通过风洞试验发现斜风向对内压动力响应的影响不明显，可见斜风向内压响应的机理还有待深入研究，国内的研究大多着眼于迎风面开孔时内压的响应问题，对斜风向内压响应的研究则很不够，因此有必要对该问题进行细致的研究。

本文采用钢结构制作的刚性开孔结构模型在风洞中进行均匀流场和湍流场作用下的内压响应风洞试验，深入研究来流风速、风向角、湍流强度、孔口特征等一系列参数变化对平均内压响应和脉动内压响应的影响，得到了一些定性和定量的规律，为斜风作用下开孔结构内压响应的进一步研究奠定了基础。

1 试验方案设计

1.1 模型设计

Vickery［3］研究指出，非刚性结构的内压动力特性会受结构本身材料柔性的影响，因此为了将结构本身的柔性排除在考察范围之外，同时为了保证模型安装的绝对刚性，本文设计了一套组合式刚性结构模型，模型由迎风面板和刚性容器组成，迎风面板采用20mm厚的钢板制作，面板平面尺寸为500mm×500mm，面板通过钢结构支撑件和底座垂直安装于风洞转盘上，采用8mm厚度的钢板制作内部空腔尺寸为250mm×250mm×100mm的刚性容器，反扣于面板后面用螺丝固定，接口处均垫上橡胶皮以保证气密性，面板中间开有一个面积为1256mm2，深度为4mm的孔口，孔口形状分为方孔、圆孔及高宽比为1∶2的矩形孔，考虑孔口处的安装空间，计算得到模型内部容积的准确值为0.0064m3，由于本文主要探索内压脉动机理，不涉及任何建筑原型，因此无需考虑内部气承刚度的模拟问题。模型设计图如图1所示，模型安装于风洞中的情景如图2所示。

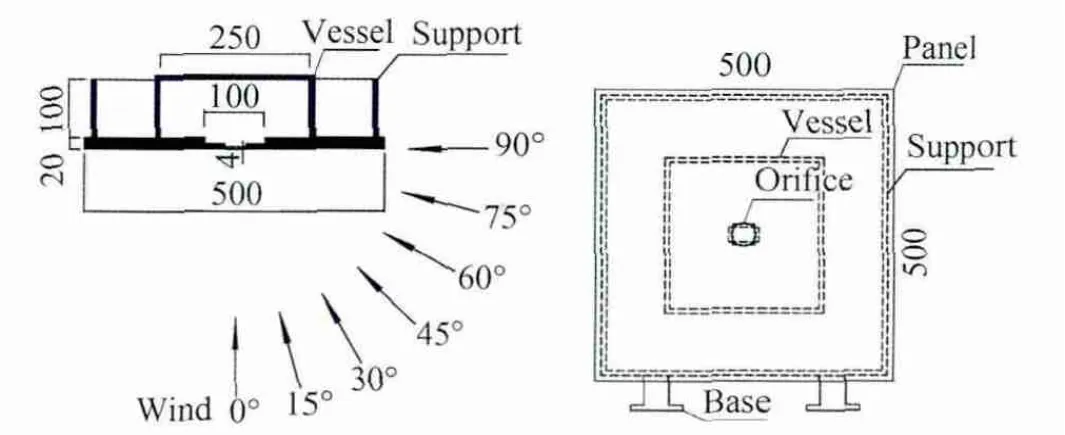
图1 刚性开孔模型设计及风向角示意图（单位：mm）Fig.1 Design of model with opening and wind angle（unit：mm）

图2 刚性开孔模型安装在风洞中的情景Fig.2 The model with opening in wind tunnel

1.2 流场模拟

本次试验在浙江大学ZD－1边界层风洞中进行，该风洞试验段截面尺寸为4m×3m，最高风速能达到55m／s，空风洞均匀流场的湍流强度约为0.5%。采用实验室自主研发的多功能流场模拟装置［16］能调试出具有不同风速与湍流强度的均匀湍流场，本文试验中的流场类型如表1所示。

表1 流场参数表Table 1 The flow field parameters

1.3 测点布置和测试方案

Liu［2］通过风洞试验发现，孔口附近的外部风压受孔口气流的影响较大，Sharma＆Richard［4］明确指出孔口封闭时的外压应该是孔口内压响应的激励源，而开孔后的孔口附近的外压已受到影响，因此本次风洞试验中分别对封闭时孔口处的平均外压系数和开孔后的内压系数在远前方来流条件完全一致的情况下分别进行测试，尽管不满足内外压同步测试的要求，但其统计结果和频域特征则是完全可以进行对比分析的。刚性容器中内压测量孔主要分布在容器背风面板的中间部分，局部布置了4个测点，同时在容器角点也布置了4个测点用于校核，校核结果表明内压相关性极高，因此本文分析采用的内压值是背风面板中间部分的其中一个测压点的数据；在封闭模型开孔处面板上均匀布置了8个测点，各测点的控制面积基本相等，本文分析采用的外压值为各外压测点的平均值。本次试验的压力测试采用Scanivalve电子压力扫描阀系统，该系统量程为 ±2500Pa，精度能达到0.1%F.S.，采样频率最高可达625Hz。所有测压点与模块的连接管路完全相同，测压管路采用经频响优化设计的管路，总长度约400mm，频响测试表明，在200Hz以内有相当平坦的频响特性，由于本文试验结果主要关注200Hz以内的导纳值，因此管路系统满足试验的要求。本次试验的采样频率采用最高值625Hz，每个工况的采样时间为32s。

2 试验结果分析

2.1 内压系数统计结果

内压系数是最直接的设计参数，因此本文从内压系数入手进行分析。图3为湍流强度为0.5%平均风速为10m／s的均匀流场中，采用孔口面积相同、深度相同形状不同的三种孔口时，模型的内压系数和相同情形下孔口封闭时孔口处的平均风压系数和均方根风压系数随风向角的变化曲线，从图中可以看出，当模型上不存在开孔时，模型开孔位置的平均风压系数与存在开孔时平均内压系数存在显著差别，文献［13］指出在迎风正面开孔时平均内压系数与平均外压系数是相等的，这一点在图3中也是成立的，然而在斜风作用下特别是风向角达到70°左右附近平均内外压系数差别最为明显，在风向角为90°附近也较为接近，这表明在背景湍流很低的流场中，在斜风作用下模型上存在单一开孔时会产生兜风效果，使得模型内部平均风压要大于不存在开孔时开孔处的平均外压，这一点与直观上的感觉是有差异的，导致的结果是当来流斜向吹向孔口时，以封闭模型孔口处的平均外压系数来等效于内部的平均风压是偏危险的，另外从图中可以看出，当孔口的面积和深度相同，仅形状不同时，对平均内压系数的影响是微不足道的。从均方根风压系数的变化曲线发现了更为奇特的情形，当风向角为50°时，模型内压均方根呈现突然爆增，风向角变大或变小时，均方根内压系数均明显下降，而当风向角为90°附近时内压脉动较大，这是由于外压脉动受特征紊流影响本身就很大。有趣的是均方根内压系数突增仅仅出现在圆形孔口和方形孔口时，矩形孔口时内压脉动增大并不明显，关于孔口形状影响的机理将在下面讨论。

图3 内压系数随风向角的变化（V＝10m／s，Iu＝0.5%）Fig.3 Variance of internal pressure coefficient with wind angle（V＝10m／s，Iu＝0.5%）

为了探索湍流强度对内压系数随风向角的变化规律的影响，将同样的模型置于湍流强度为10%且平均风速仍为10m／s的湍流场中进行同样的试验，结果如图4所示。从图中看出，不同孔口形状时的平均内压系数略有差别，而斜风向作用下封闭模型孔口处平均风压系数小于有孔口时模型内部平均压力系数，这一点与均匀流场中的情形相似，表明斜风向孔口兜风效果仍然存在。而从均方根风压系数曲线图中并未发现前述的内压脉动爆增现象，内压脉动与外压脉动较为接近，这说明当湍流强度较大时，内压脉动机理与均匀流场有一定差异，其机理将在下面进行深入分析。

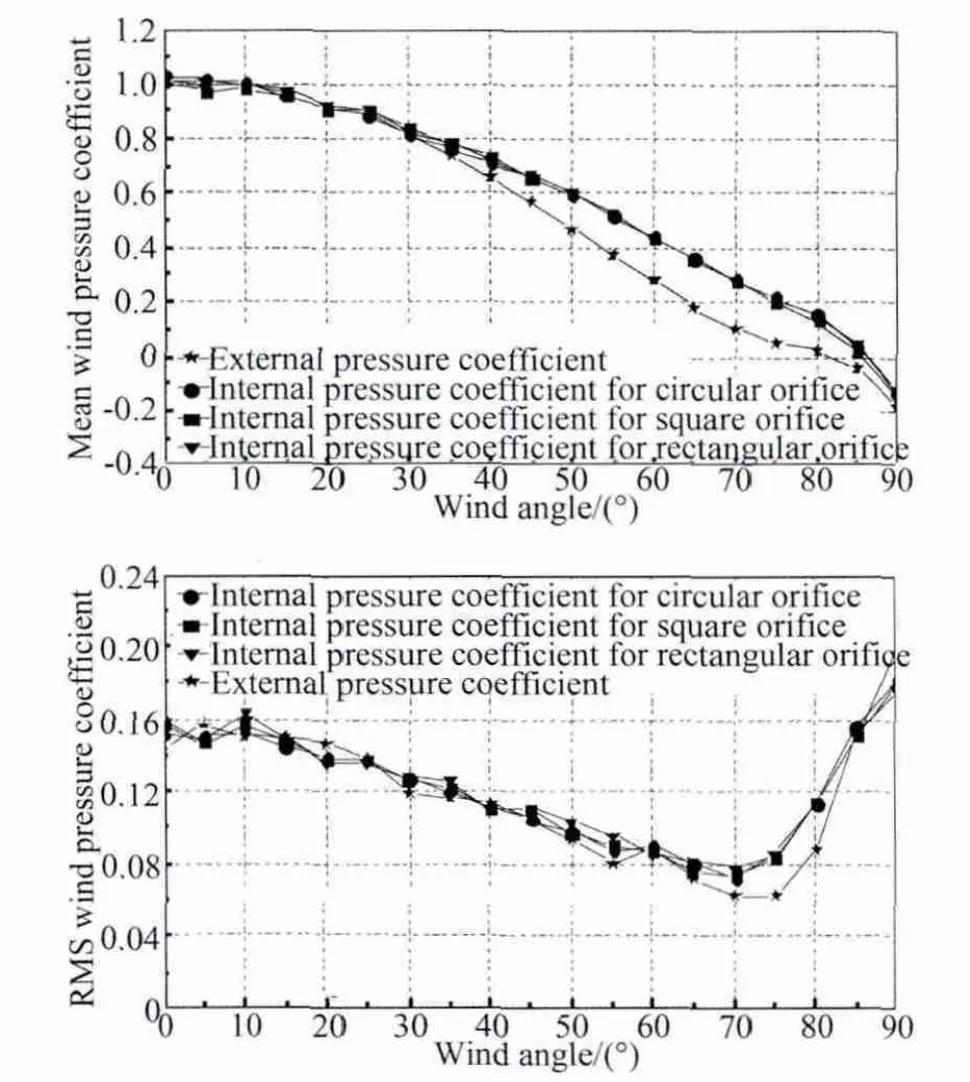
图4 内压系数随风向角的变化（V＝10m／s，Iu＝10%）Fig.4 Variance of internal pressure coefficient with wind angle（V＝10m／s，Iu＝10%）

从上述试验结果不难发现，在特定的孔口特征和均匀流场中内压脉动响应在一定的风向角下会出现爆增现象。为了进一步探索风速大小对这一现象的影响，本文对方形孔口模型在均匀流场中进行风速为5m／s、10m／s、15m／s、20m／s的试验。各风速下平均内压系数与平均外压系数的差值和均方根内压系数与均方根外压系数的比值随风向角的变化曲线如图5所示。可以看出各风速下平均内压系数与平均外压系数的差值相差不大，仅5m／s时略有差别，这不排除测试精度的影响，但可以肯定的是各风速下内外压系数的差值在55°～75°风向角下最大，达到0.2以上。均方根内压系数与均方根外压系数的比值则随风速的影响很大，在风速为5m／s时均方根内压系数与均方根外压系数的比值在45°风向角时达到最大但仅为1.7，而风速为10m／s时其比值在50°时达到最大达到8.0，风速为15m／s和20m／s时其比值在55°时达到最大分别达到11.5和16.1，可见风速大小对内压脉动产生了很大的影响，有必要对其产生机理进行深入研究。

2.2 内压系数谱和导纳曲线分析

为了更清楚了解内压动力响应特性，首先对内外压系数功率谱进行分析，图6为10m／s风速下0°风向角下方孔模型内外压系数功率谱曲线。从图6中可以看出，0°风向角下内压谱出现明显的共振现象，

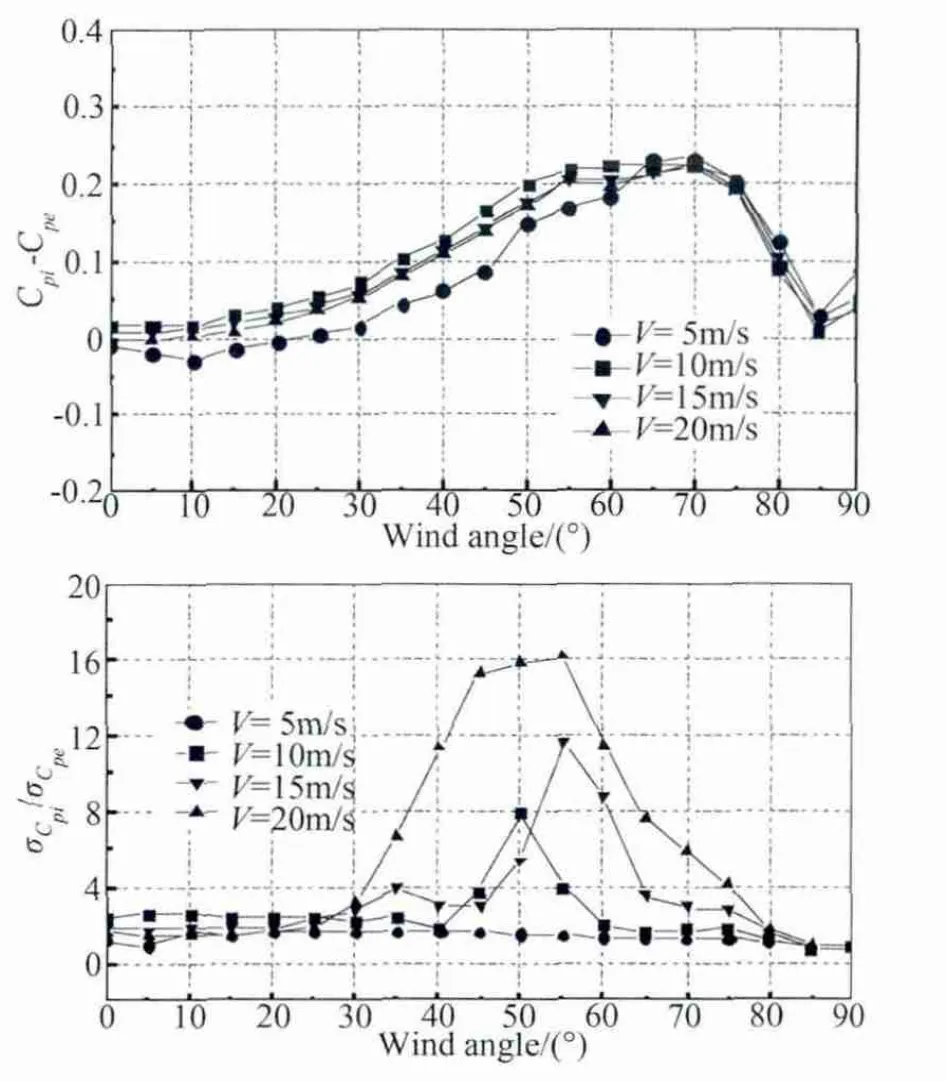
图5 不同风速下内外压系数随风向角的变化Fig.5 Variance of internal and external pressure coefficient with wind angle under different wind velocities

图6 0°风向角模型内外压系数谱（V＝10m／s，Iu＝0.5%）Fig.6 Internal and external pressure coefficient spectra of model under wind angle of 0°（V＝10m／s，Iu＝0.5%）

采用Vickery［3］提出Helmholtz频率计算公式：

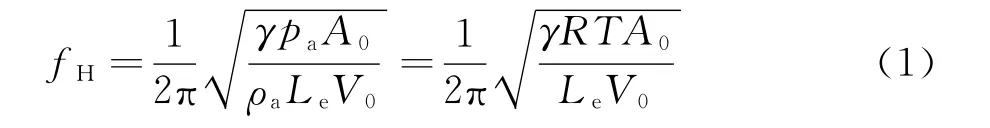
式中，ρa为空气密度，pa为大气压，γ为等压过程气体比热与等容过程气体比热之比，R为空气的气体常数，T为空气绝对温度，A0为孔口面积，V0为空腔体积，Le为孔口气柱长度，即其中L0为孔口实际深度，根据试验时气温为T＝303K，取γ＝1.4，R＝287J／（kg·K），CI＝ 0.886［3］，并将模型几何参数代入式（1），得到的共振频率理论值为131Hz，与图6中的共振频率非常接近，因此可以认定此时的内压共振现象即为Helmholtz共振现象。将内压系数功率谱与外压系数功率谱的比值定义为内压的导纳，风向角为0°、25°和55°的方孔模型内压导纳曲线结果绘于图7中，图7（a）中的共振频率为132Hz，显然为Helmholtz共振频率，说明在0°风向角下即迎风正面开孔时，内压产生了Helmholtz共振，在图7（b）中则发现了两个共振峰，除了频率为132Hz的Helmholtz共振外，频率为45Hz的共振峰则显然是由于斜风通过孔口的气流在孔口处造成涡脱落所形成，说明在25°风向角作用下，孔口处产生的涡脱能量直接传递到模型内部，而图7（c）内压导纳曲线中则又只出现一个共振峰，共振峰的频率为142Hz，共振频率比前面的Helmholtz共振频率要高一些，而共振峰值则是前面Helmholtz共振峰值的几百倍，产生了很大的内压脉动，说明在55°风向角下，涡脱造成的气流振动与Helmholtz共振合而为一，产生了更为剧烈的共振。图8为方孔模型0.5%湍流度10m／s风速下内压共振频率及导纳峰值对数随风向角的变化曲线，其中导纳峰值对数以误差的形式描述，从图中可以看出，当风向角较小时，内压导纳图上只出现一个共振峰，即Helmholtz共振峰，当风向角达到20°时，开始出现双共振峰，涡脱能量并不是很大，随着风向角增大，涡脱频率随之增大，受涡脱气流影响内压的Helmholtz共振频率大小产生了较大的波动，产生波动的原因可以认为是孔口的涡脱现象扰乱了孔口振荡气柱的长度，从而改变了振荡气柱的质量；另一方面，从共振能量的角度还可以发现，在风向角达到50°左右时，内压共振的能量明显增大，其中50°时136Hz处的内压导纳峰值甚至达到1×105，此时涡脱能量逐步融入到Helmholtz共振中，可以认为此时产生了强烈的涡激内压共振，当风向角大于60°时，内压涡激共振的能量显著减小，涡脱的影响消失，从图8的内压导纳共振频率和共振峰值的变化就不难理解图5中内压脉动在50°风向角附近会产生突然增大。

图7 不同风向角下内压系数导纳曲线（V＝10m／s，Iu＝0.5%）Fig.7 Internal pressure coefficient admittance curves for different wind angles（V＝10m／s，Iu＝0.5%）

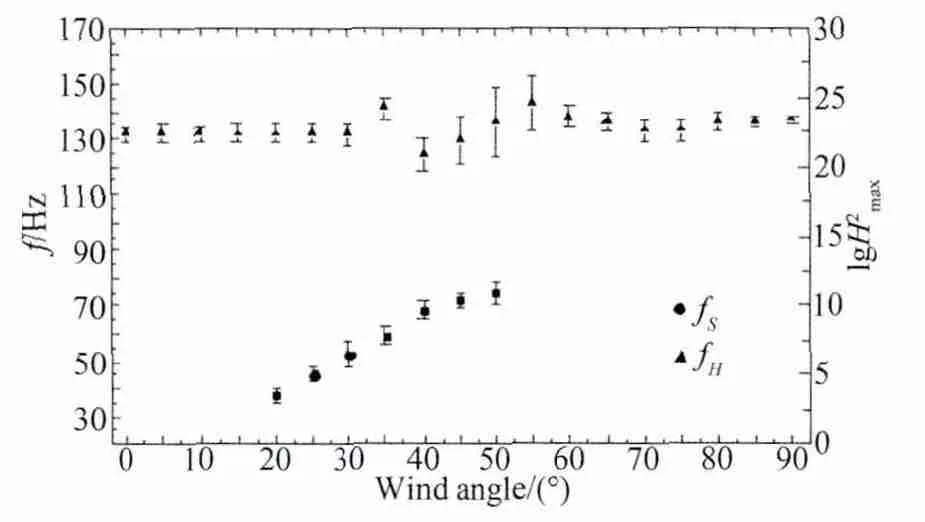
图8 内压共振频率及导纳峰值对数随风向角的变化曲线（V＝10m／s，Iu＝0.5%）Fig.8 The frequency and the logarithm of admittance peaks with wind angles（V＝10m／s，Iu＝0.5%）

2.3 湍流强度对内压涡激共振的影响

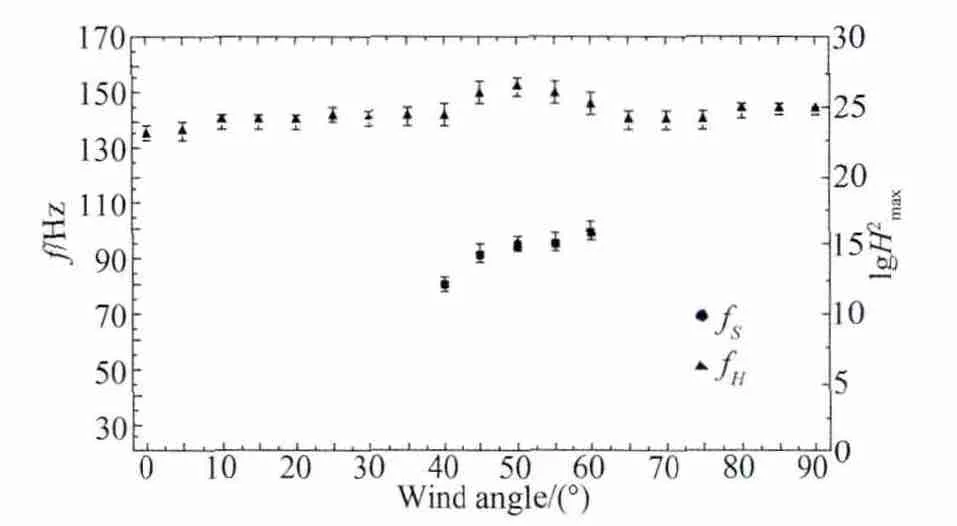
图9 内压共振频率及导纳峰值对数随风向角的变化曲线（V＝10m／s，Iu＝10%）Fig.9 The frequency and the logarithm of admittance peaks with wind angles（V＝10m／s，Iu＝10%）

图10 内压共振频率及导纳峰值对数随风向角的变化曲线（V＝10m／s，Iu＝20%）Fig.10 The frequency and the logarithm of admittance peaks with wind angles（V＝10m／s，Iu＝20%）

为了探索内压涡激共振的产生机理，本节将对影响涡激共振的其中一个外部因素，即来流的湍流强度进行对比研究，在试验中分别采用10%和20%湍流强度的湍流场对方孔模型在10m／s平均风速下进行同样的试验，分别得到了两种情况下内压共振频率及导纳峰值对数随风向角的变化曲线分别如图9和图10所示，从图9中可以发现，湍流度达到10%时，孔口涡脱现象仍然出现，与均匀流场相比涡脱频率略有提高，涡脱能量大幅下降，尽管涡脱气流对内压Helmholtz共振的影响仍然存在，但涡激内压共振现象并不明显，特别是55°风向角下出现的内压导纳最大峰值仅仅为101.6，对内压脉动均方根产生的影响极为有限；而从图10中则发现，湍流度为20%时，涡脱现象已完全消失，当然其对内压Helmholtz共振的影响也不复存在，随着风向角的变化，内压共振频率和导纳峰值变化不大。从上述现象不难看出湍流强度是影响内压涡激共振的重要因素，湍流强度越小，产生涡激内压共振的可能性越大。

2.4 来流风速对内压涡激共振的影响

对于另一个外部因素即来流风速对内压涡激共振的影响研究，本文只选择了内压涡激共振最为显著的均匀流场进行试验，图11为方孔模型在0.5%湍流度5m／s风速下内压共振频率及导纳峰值对数的曲线，从图中可以看出，当风速很小时，尽管湍流度很小，但孔口处不出现涡脱现象，随着风向角变化，内压Helmholtz共振频率基本上保持不变，且内压导纳峰值波动很小，这说明只有风速达到一定时，才会出现孔口气流涡脱现象，图8表明当风速达到10m／s时涡激内压共振的现象已相当明显。图12和图13为方孔模型在0.5%湍流度15m／s风速和20m／s风速下内压共振频率及导纳峰值对数的曲线，与图8对比可以发现，当来流风速为15m／s和20m／s时，孔口处的涡脱现象均非常明显，随着涡脱频率的增大，内压的Helmholtz共振频率向高频移动，显然此时产生的孔口强大涡流将孔口振荡气柱长度大幅削减，而当风向角增大到孔口涡脱频率与内压Helmholtz共振频率相近时，形成能量极强的涡激内压共振，此时原来的Helmholtz共振峰被完全融入了涡激内压共振中。对比图12和图13的曲线不难看出，当风速较大时，相同风向角下的涡脱频率较高，产生内压涡激共振的风向角会较小些，可以推测的是，当风速更大时，发生涡激内压共振的风向角会更小，而这时对内压抗风设计会更为不利。综上所述，来流风速对内压涡激共振的影响非常显著，当风速很小时孔口不产生涡脱效应，内压Helmholtz共振是内压共振的主导力量，当风速增大到一定程度时，孔口产生涡脱效应，在一定程度上影响内压Helmholtz共振，并产生了涡激内压共振现象，而当风速很大时，孔口涡脱的影响很大，甚至成为涡激内压共振的主导因素。

Fig.11 内压共振频率及导纳峰值对数随风向角的变化曲线（V＝5m／s，Iu＝0.5%）Fig.11 The frequency of internal pressure and the logarithm of admittance peaks with wind angles（V＝5m／s，Iu＝0.5%）

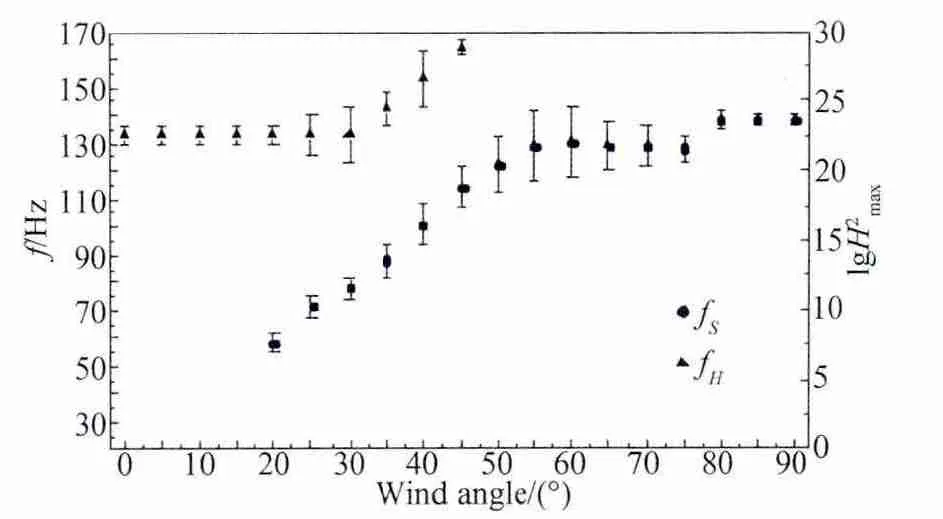
图12 内压共振频率及导纳峰值对数随风向角的变化曲线（V＝15m／s，Iu＝0.5%）Fig.12 The frequency of internal pressure and the logarithm of admittance peaks with wind angles（V＝15m／s，Iu＝0.5%）

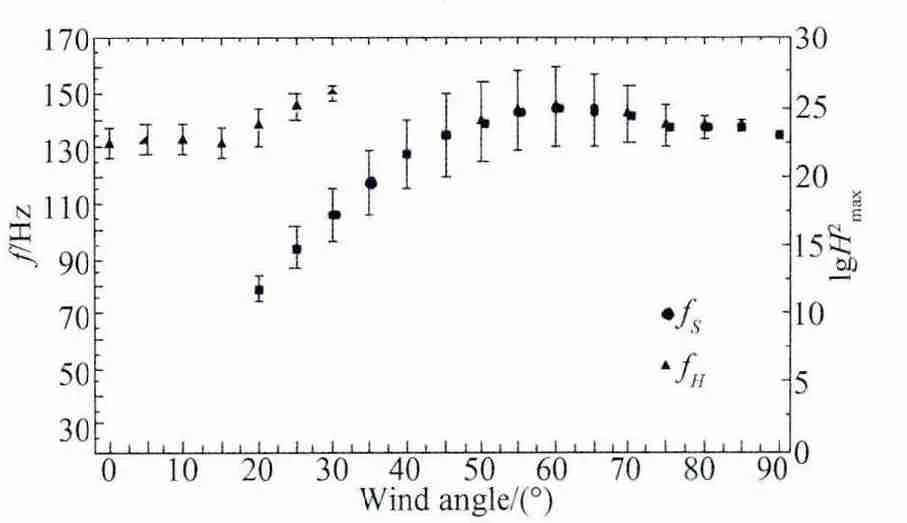
图13 内压共振频率及导纳峰值对数随风向角的变化曲线（V＝20m／s，Iu＝0.5%）Fig.13 The frequency of internal pressure and the logarithm of admittance peaks with wind angles（V＝20m／s，Iu＝0.5%）

根据结构涡激共振理论，涡脱频率与斯特拉哈数有关，由于斜风作用下孔口处的涡脱频率与通常理论的柱体涡脱是有一定区别的，因此不能简单套用柱体斯特拉哈数来研究内压涡激共振问题，参考Sharma＆Richard［14］的提法，本文定义孔口斯特拉哈数为：

其中，V 为来流风速，D 为孔口特征尺寸，fH为Helmholtz共振频率。根据本文的试验条件和结果，当孔口斯特拉哈数大于等于0.92时，不会发生内压涡激共振，当孔口斯特拉哈数小于等于0.47时，会发生内压涡激共振。Sharma＆Richard［14］在试验中得到发生涡激内压共振的孔口斯特拉哈数为0.44，Demetz＆Farabee［17］则认为发生涡激内压共振的孔口斯特拉哈数必须大于等于0.2，本文的试验结果与国外专家的研究结果相差不大，但由于试验条件不同所得结果略有不同。

2.5 孔口形状对内压涡激共振的影响

除了外部流场因素，模型本身也是影响内压涡激共振的重要因素，本文针对方孔、圆孔及高宽比为1∶2的矩形孔三种孔口的模型，从图3内压系数随风向角的变化便发现孔口形状对内压共振有很大影响，图14和图15为高宽比为1∶2的矩形孔和圆孔模型在0.5%湍流度10m／s风速下内压共振频率及导纳峰值对数的曲线。与图8对比发现，相同风向角下矩形孔的涡脱频率最高，方孔的涡脱频率最低，这是由于在斯特拉哈数相同的情况下，孔口高度越小，涡脱频率越高；而内压涡激共振现象则是方孔模型最明显，矩形模型最不明显，这一现象可以认为是矩形开孔短边的脱落涡流不能与整个孔口的振荡气柱相匹配，从而无法激起较强的内压共振。由于三个不同形状的孔口位于大面板的中部，孔口边缘与侧墙边缘的距离基本相等，因此在其它条件相同的情况下，扁矩形孔口有利于抑制涡激内压共振的发生。

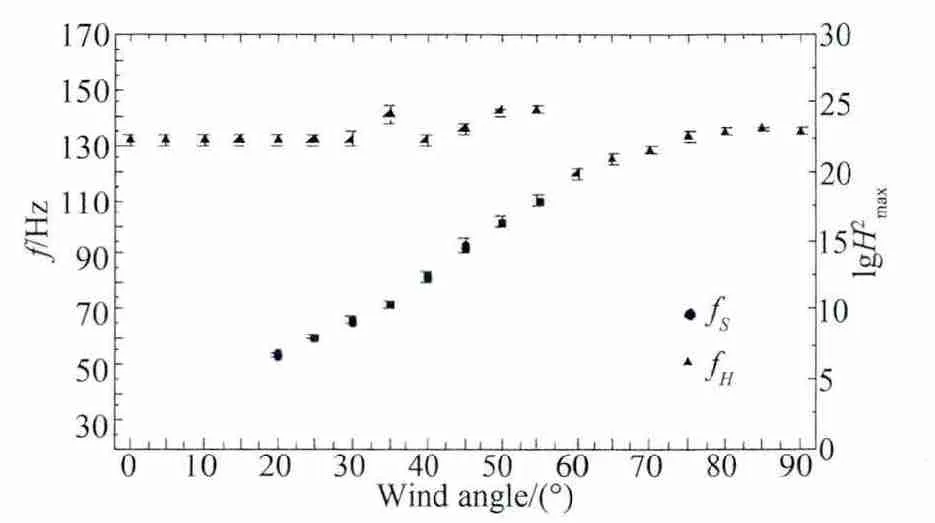
图14 矩形孔模型内压共振频率及导纳峰值对数随风向角的变化曲线（V＝10m／s，Iu＝0.5%）Fig.14 The frequency and the logarithm of admittance peaks with wind angles for rectangular orifice（V＝10m／s，Iu＝0.5%）

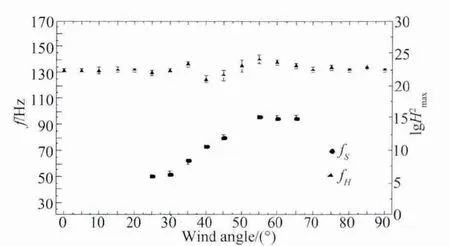
图15 圆孔模型内压共振频率及导纳峰值对数随风向角的变化曲线（V＝10m／s，Iu＝0.5%）Fig.15 The frequency and the logarithm of admittance peaks with wind angles for circular orifice（V＝10m／s，Iu＝0.5%）

2.6 内压涡激共振的工程应用前景

风致内压涡激共振现象是对风致内压响应问题的重要补充，一般认为迎风面开孔时内压响应较大，会对结构产生最不利的影响，而发现内压涡激共振现象以后，需要承认在某些情形下斜风向的内压总荷载有可能超过迎风面正风向的内压总荷载，这一现象有可能出现在来流湍流强度较小且风速较高的高层或超高层建筑上部的局部内压，由于斜风向导致的内压涡激共振造成内压峰值很可能远远超过抗风设计值，这一点需要引起设计关注。

从另一个角度，由于内压涡激共振产生了高频的气柱共振类似于吹笛，在风速很高时甚至会产生刺耳的啸叫声，因此如何在工程实际中减少产生这种内压涡激共振效应是降低气流啸叫的重要措施，本文的研究在一定程度上解释了内压涡激共振的产生机理，为进一步研究奠定了基础。

3 结 论

本文针对刚性开孔结构模型在风洞中进行均匀流场和湍流场作用下的内压响应风洞试验，研究了来流风速、风向角、湍流强度、孔口特征等一系列参数变化对平均内压响应和脉动内压响应的影响，讨论了内压涡激共振产生的机理，得到了一些有益的规律：

（1）斜风向作用下开孔结构平均内压系数与不存在孔口时孔口处平均外压系数存在一定区别，开孔后产生兜风效应，且孔口形状不同及湍流强度不同时均存在，当来流斜向吹向孔口时，以封闭结构孔口处的平均外压系数来等效于内部的平均风压是偏危险的。

（2）在斜风向作用下开孔结构内压会产生涡激共振现象，导致内压脉动大幅增大，产生涡激内压共振与孔口特征、来流风速、湍流强度及风向角有关，湍流强度越小、风速越高，涡激内压共振发生的可能性越大，扁矩形孔口有利于抑制内压涡激共振的发生。

［1］HOLMES J D.Mean and fluctuating pressures induced by wind［A］.Proc.5th Int.Conf.on Wind Engineering［C］.USA：Fort Collins，1979，（1）：435－450.

［2］LIU H，SAATHOFF P J.Building internal pressure：sudden change［J］.Journal of Engineering Mechnics，Division，ASCE，1981，107（Em2）：309－321.

［3］VICKERY B J，BLOXHAM C.Internal pressure dynamics with a dominant opening［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，41－44：193－204.［doi：10.1016／0167－6105（92）90409－4］

［4］SHARMA R N，RICHARDS P J.Computational modeling in the prediction of building internal pressure gain functions［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67＆68：815－825.［doi：10.1016／S0167－6105（97）00121－9］

［5］SHARMA R N，RICHARDS P J.Computational modeling of the transient response of building internal pressure to a sudden opening［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，72：149－161.［doi：10.1016／S0167－6105（97）00244－4］

［6］SHARMA R N，RICHARDS P J.The effect of roof flexibility on internal pressure fluctuations［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，72：175－186.［doi：10.1016／S0167－6105（97）00252－3］

［7］YU S C，LOU W J，SUN B N.Wind－induced internal pressure fluctuations of structure with single windward opening［J］.Journal of Zhejiang University Science A（Science in Engineering），2006，7（3）：415－423.［doi：10.1631／jzus.2006.A0415］

［8］YU S C，LOU W J，SUN B N.Wind－induced internal pressure response for structure with single windward opening and background leakage［J］.Journal of Zhejiang University Science A，2008，9（3）：125－132.［doi：10.1631／jzus.A071271］

［9］GUHA T K，SHARMA R N，RICHARDS P J.Internal pressure dynamics of a leaky building with a dominant opening［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99：1151－1161.［doi：10.1016／j.jweia.2011.09.002］

［10］HOLMES J D，GINGER J D.Internal pressures－The dominant windward opening case－A review［J］.Journal of Wind Engineering and Industrial Aerodynamics，2012，100：70－76.［doi：10.1016／j.jweia.2011.11.005］

［11］LIU H，RHEE K H.Helmholtz oscillation in building models［J］.Journal of Wind Engineering and Industrial Aerodynamics，1986，24：95－115.［doi：10.1016／0167－6105 （86）90001－2］

［12］WOODS A R，BLACKMORE P A.The effect of dominant openings and porosity on internal pressures［J］.Journal of Wind Engineering and Industrial aerodynamics，1995，57：167－177.［doi：10.1016／0167－6105（95）00003－A］

［13］YU S C，LOU W J，SUN B N，et al.Wind tunnel research on internal wind effect for structure with openings［J］.Journal of Building Structures，2007，28（4）：76－82.（in Chinese）余世策，楼文娟，孙炳楠，等.开孔结构内部风效应的风洞试验研究［J］.建筑结构学报，2007，28（4）：76－82.

［14］SHARMA R N，RICHARDS P J.The influence of Helmholtz resonance on internal pressure in low－rise building［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91：807－828.［doi：10.1016／S0167－6105（03）00005－9］

［15］OH J H，KOPP G A，INCULET D R.The UWO contribution to the NIST aerodynamic database for wind loads on low buildings：Part 3.Internal pressures［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95：755－779.［doi：10.1016／j.jweia.2007.01.007］

［16］YU S C，JI X H，HU Z H，et al.Wedge and retainer combined device for boundary layer simulation in wind tunnel［P］.China，201010298629.0，2011－12－21.（in Chinese）余世策，冀晓华，胡志华，等.风洞边界层模拟的尖劈隔栅组合装置［P］.中国，201010298629.0，2011－12－21.

［17］DEMETZ F C，FARABEE T M.Laminar and turbulent shear flow induced cavity resonances［R］.AIAA 77－1293，1977.