基于IBVCM的二维非定常动边界数值模拟研究

卢海天，吴 杰，赵 宁

（南京航空航天大学 空气动力学系，南京 210016）

0 引 言

随着仿生学和流体力学的发展，鱼类的游动机理以及推进力与游动参数的关系成为当前研究的热点。根据鱼游动的特性，人们已经初步研制出了具有较好性能的仿生鱼。但是，就目前而言，仿生鱼中仍待解决的问题包括：（1）鱼类推进理论模型以及游动算法的研究；（2）在研制上，选择合适的材料和动力实现仿生鱼机构的最优；（3）仿生鱼控制技术的研究，解决推进与稳定的相互制约；（4）数值模拟上，涉及到单一鱼体的纵向前进和对于多个鱼的游动及其协作问题，成果尚不显著。

相对于实验研究，数值计算模拟具有研究周期短、费用少等实验无法替代的优势。自20世纪60年代开始，许多来自不同领域的学者对鱼游动做出了大量的数值模拟研究。通过分析数值结果，可以获得相关参数对鱼游动的影响，从而为仿生鱼的设计和优化提供依据。其中，1960年Lighthill［1］率先对体形瘦长的鳗鲡模式游动的鱼提出了细长体模型，得到了定常线性化解。1973年Newman分析了在无粘流体下鱼体表面的作用力，计算出鱼体表面压力公式［2］。由于考虑鱼体厚度的影响，Newman得出与早期Lighthill，Wu和Newman研究细长型鱼体时不同的诱导阻力结果。80年代中后期童秉纲［3］等建立了模拟鱼类游动的三维波动板理论（3DWPT），采用势流理论的三维非定常涡格法在频域内求解，研究了各类鱼的推进性能。1996年Liu和Wassersug应用一种新的二维CFD建模方法研究蝌蚪的游动［4］，得出蝌蚪能够产生高效的推进力，而且其运动特性与自身形状有关。

鱼游动是典型的非定常动边界问题，它对传统的数值模拟方法提出了巨大的挑战。目前，已经形成的一些数值方法可以有效地模拟此类问题。其中比较典型的是由Peskin［5］在1977年提出的浸入边界方法（IBM）。它较好地模拟了动边界的流动问题，但其主要缺点是在边界处不能保证无滑移条件。另一种数值模拟是格子波尔兹曼方法（LBM）。它简洁且易于实现，没有涉及到微分方程以及相应的代数方程［6－9］。

本文采用格子波尔兹曼方法（LBM）和浸入边界速度修正方法（IBVCM）相结合，仅研究鱼体在摆动的模式下影响其推进力的一些基本参数。涉及到的基本参数有鱼的形状、频率、波长和雷诺数，通过逐个参数以及参数组合的形式分析影响鱼摆动的基本规律。此外，从旋涡分布的角度出发，分析并得到旋涡变化与鱼身运动的相互关系。和传统的IBM相比，本文的方法更精确地满足无滑移边界条件，从而更适合模拟动边界的流动问题。

1 数值研究方法与鱼摆动的数学模型

1.1 浸入边界速度修正方法（IBVCM）

由于在传统的IBM中，体积力是预先设定的，不能保证由修正的速度场插值得到的边界速度满足无滑移条件。为了克服这一难点，本文采用IBVCM对浸入边界方法进行修正［10］。IBVCM的基本思想是不预设体积力，而是先由周围流场插值得到壁上的速度，再使该速度满足边界无滑移条件，从而实现物体上的边界速度与流体的边界速度相等。

如图1所示，粗实线表示物体边界，可以看出物体边界与网格的交点Mx与My。根据动量方程，点Mx仅仅影响点A与点B速度分量u的修正，点My仅仅影响点B与点C速度分量v的修正。点A、点B和点C的速度分量分别表示为（uA，vA）、（uB，vB）、（uC，vC），由流场x方向插值得到点Mx处的速度分量表示为（uix，vix），由流场y方向插值得到点My处的速度分量表示为（uiy，viy）。此外，点Mx处的壁上速度表示为（uMx，vMx），点My处的壁上速度表示为（uMy，vMy）。由线性插值，边界点Mx的插值速度［11］为：

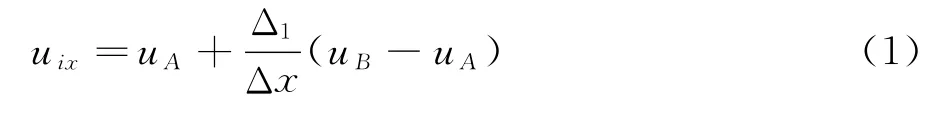
边界点My的插值速度为：

则点A与点B之间的速度修正为：

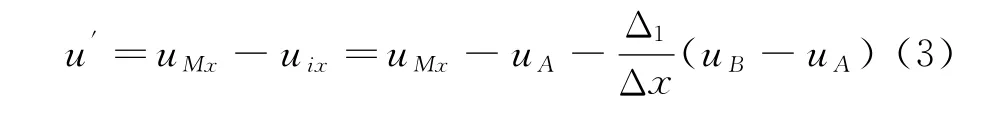
可以看出，当点A与点B的速度分量u由式（3）得到修正后，点Mx处的插值速度满足边界条件u＝uMx。

类似地，点B与点C之间速度修正为：

某些情形下，比如在一个网格间距内网格线与边界不止有一个交点时，所有的速度分量都应进行修正。

图1 笛卡尔网格线，浸入边界和它们的交点Fig.1 Cartesian mesh lines，immersed boundary and their intersection points

1.2 格子波尔兹曼方法（LBM）

格子波尔兹曼方法是一种以介观动理学模型为基础的数值模拟方法。与传统的数值方法相比，LBM的主要优势在于计算简单且容易实现。在本文的数值模拟中，IBVCM用于处理鱼的边界速度修正，而LBM用于求出笛卡尔网格线上的中间速度场信息。这样，就把两种方法进行了耦合。这里，格子波尔兹曼方程为：

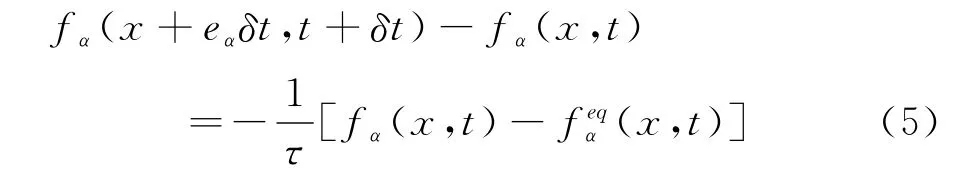
其中，τ是单松弛时间，fα是分布函数，是局部平衡分布函数，δt是时间步长，eα是粒子速度。在本文的LBM计算中使用D2Q9格子速度模型。这样，eα可以描述为：

而平衡分布函数为：

其中，对于α＝0，wα＝4／9；α＝1～4，wα＝1／9；α＝5～8，wα＝1／36。式（7）中的密度ρ与速度V是修正速度场在上一个时间层上的值，可以看出修正速度场对分布函数fα的影响是通过平衡分布函数体现的。由质量与动量守恒关系，宏观密度ρ与流体速度V按照密度分布函数可计算为：

综上所述，沿时间方向，当鱼体每一次变形时，本文LB－IBVCM的基本求解步骤为：

（1）设体积力为0，应用LBM求解流场运动得到中间速度场；

（2）根据式（3）和式（4）将物体边界与网格线交点周围的网格点速度进行一次修正。

1.3 鱼摆动的数学模型

Videler（1993）在研究中发现鱼体的横向对称运动可以由傅里叶级数中奇数项的前三项来精确地描述［12］。考虑到第三个之后的频率项与第一个频率项相比非常小，在忽略高频之后，鱼体中线的运动可以描述为：

其中ym（x，t）是y方向的中线坐标，a1（x）和b1（x）表示傅里叶因子，f是行波的频率，t是时间，x是x方向的坐标。将a1（x）和b1（x）表示为：

可以更进一步地推导出公式：

此处，l表示波长，w＝2πf表示圆频率，am（x）表示波幅。对式（11）关于时间t求导，得出鱼体中线各个点做横向运动时的速度：

波幅可以选取二阶多项式函数的形式，基于大量的数值模拟研究，在本文中取为：

2 鱼摆动的数值模拟及参数分析

本文对影响鱼类摆动的基本参数：形状，频率，波长和雷诺数，采用逐一以及组合的形式进行分析。具体研究的问题是，给定自由来流速度U，模型在流向固定，而在垂直于来流方向鱼体中线的各个点做形如式（11）所示的摆动，通过结果分析从而得出影响鱼类摆动的一些基本结论。鱼体表面必须满足无滑移边界条件。雷诺数定义为：Re＝UL／ν，L为鱼体长度，ν是运动粘度。升力系数与阻力系数定义为：

其中ρ为流场密度。FL和FD分别为升力和阻力，它们分别通过控制体积法求出。对矩形控制体Ω通过积分动量方程得：

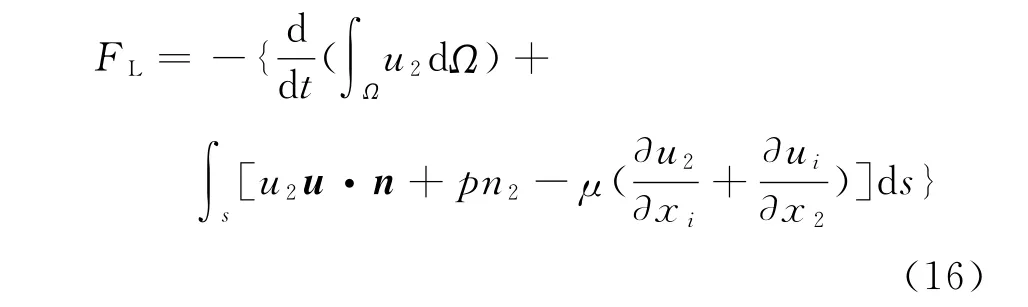
其中S是控制体外表面，n＝（n1，n2）是控制体表面边界的法向量，下标1，2分别表示x方向与y方向。

为了验证本文的方法，选取Re＝3000，波长l＝0.87，频率f＝1.3，模拟了NACA0012翼型形状的鱼摆动，所得的阻力系数为0.062，与文献［10］中阻力系数0.06基本一致。这说明本文采用的LB－IBVCM可以很好地模拟鱼类的摆动问题。

2.1 网格的划分

在本文的研究中，计算区域采用非均匀网格。但在鱼体周围采用均匀网格，尺寸为120×120，其步长为0.01。整个流场区域的网格为501×351。流场区域如图2所示。考虑到标准的LBM只能应用于均匀网格，所以本文采用基于泰勒级数展开和最小二乘方的LBM（TLLBM）处理非均匀网格［13］。

图2 流场区域Fig.2 The flow field

2.2 鱼体形状的影响

本文总共选取五种形状作为鱼体模型进行分析，分别 是 RoboTuna、NACA0006、NACA0012、NACA2412、NACA2424。其中，RoboTuna模型［14］为：

如图3所示，选取Re＝400，l＝1和w＝4，研究不同形状鱼体的阻力系数关于时间的变化关系。另外固定Re＝400，分别研究不同形状鱼体的阻力系数关于频率和波长的变化关系，如图4所示。可以看出，NACA0012和NACA2412翼型的平均阻力相接近，而且均大于NACA0006的阻力，但远小于Robo－Tuna和NACA 2 4 2 4的阻力。这很好地说明了弯度对阻力的影响不大，而厚度对阻力影响较大。鱼的厚度越大，阻力越大。其原因为厚度越大，流经翼型后的逆压梯度越大，流体越容易分离，从而大大加宽了尾流，导致压差阻力增大。

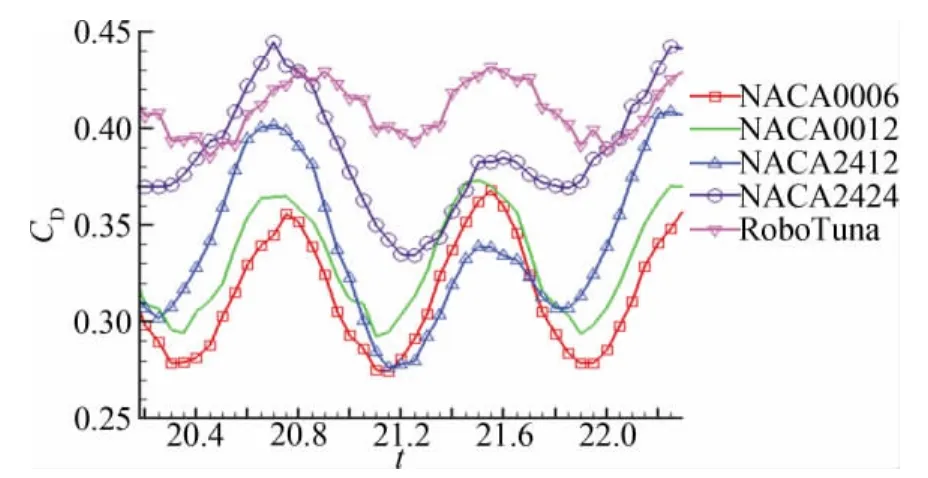
图3 Re＝400，l＝1和w＝4时，不同鱼体形状下鱼摆动的阻力系数Fig.3 The drag coefficient of fish swimming for different body shapes at Re＝400，l＝1and w＝4

图4 不同鱼体形状时的阻力系数Fig.4 The drag coefficient for different body shapes

2.3 频率和波长的影响

对于本文中的鱼摆动而言，推进力是负的阻力。这主要由于在涡沿着鱼体脱落的过程中，上表面的涡从尾尖处脱落至鱼体中线的下侧，而下表面的涡从尾尖处脱落至中线的上侧，这就形成了逆卡门涡街，从而产生推进力。由图4（a）可以看出，随着w的增加，推进力以及曲线斜率均增大。另外也可看出，Robo－Tuna产生推进力的临界频率是w＝14.1，而NACA0012与NACA2412翼型的临界频率约在w＝12.8。

如图4（b）所示，可以看出当波长在0.7～1.3的范围内时，阻力系数随着波长的增大而减小。对于NACA0012翼型，在Re＝400和w＝4时，图5给出了不同波长下升力系数与阻力系数的关系。可以看出，不同波长下的相位图均为关于CL＝0对称且类似于蝴蝶形状的图形，可知阻力系数的频率为升力系数的两倍，升力系数的平均值为0。其原因是鱼的形状是对称的，来流初始平行于鱼体中线，中线上各点亦做横向对称运动。而且当波长由0.9增大至1.3时，CL的幅度一直在增大，曲线向左移，平均阻力减小。这主要因为在波长的研究中，行波的相速度Cp（Cp＝lf）均大于来流速度U。随着波长的增大，比值Cp／U增大，鱼体周围的扰动被进一步遏制，流体不易分离，鱼体表面的应力减小，从而导致阻力减小［15］。

2.4 频率、波长、雷诺数的综合影响

由于国内外很多工作都是关于大雷诺数的研究，而低雷诺数的研究不多见，所以本文仅分析低雷诺数对推进力的影响。

图5 Re＝400，w＝4，不同波长下升力系数与阻力系数的相位图Fig.5 Drag and lift coefficient phase diagram varies with wavelength at Re＝400and w＝4

对于NACA0012翼型，为了研究波长以及雷诺数的影响，如图6（a）所示，给定w＝14，分析了l＝1和1.7以及不同雷诺数下的推进力。当波长由1增大至1.7后，曲线下移，可知增大雷诺数与波长可使推进力增大。对于l＝1.7，在Re≥50时即可产生推进力。为了研究雷诺数和频率的影响，如图6（b）所示，给定l＝1，分析了Re＝100和500以及不同频率下的推进力。当雷诺数由100增大至500后，曲线下移，可知增大雷诺数与频率可使推进力增大。在Re＝100时，只有w≥15.6时，才产生推进力。而对于Re＝500，当w≥12.5时即可产生推进力，且平均无量纲推进力可达0.63或更多。

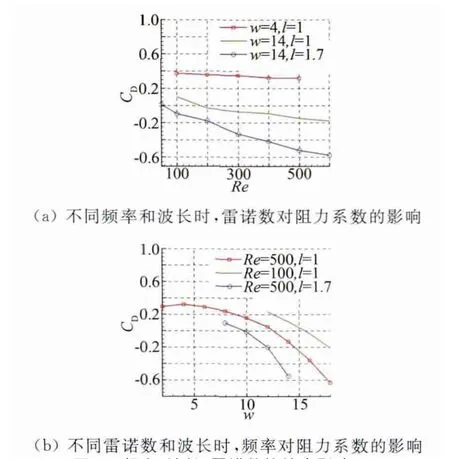
图6 频率、波长、雷诺数的综合影响Fig.6 The combined effects of frequency，wavelength and Reynolds number

2.5 旋涡分析

在图6（b）中，当Re＝500，l＝1和w＝18时，产生的推进力系数为0.63。图7显示了在此运动模式下尾尖沿y方向运动与推进力的变化。对图中A点与B点进行分析，相应时刻的涡分布分别如图8与图9所示。可以发现，A点的推进力最大，B点的推进力近似为零。鱼的运动与涡的存在，是导致A点与B点推进力差异的主要原因。为了分析尾尖运动对推进力的影响，本文对A点与B点处的旋涡运动进行了分析。

图7 阻力系数与鱼摆动时相应的尾尖的垂直位置Fig.7 The drag coefficient and corresponding vertical location of tail tip of fish swimming

图8 A点的涡分布Fig.8 The vortex distribution for pointA

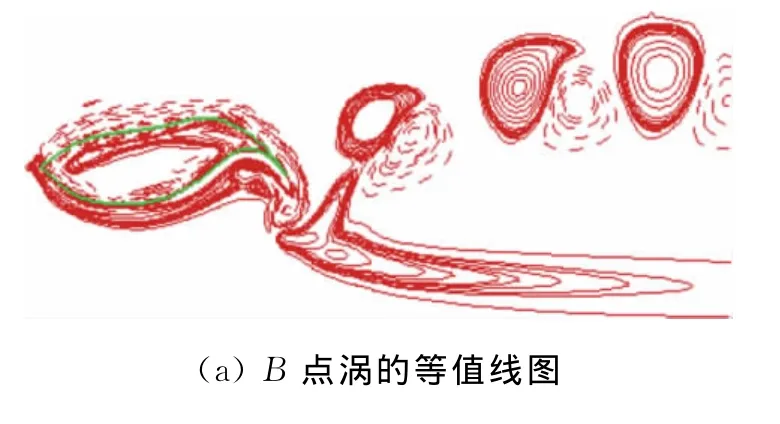
图9 B点的涡分布Fig.9 The vortex distribution for point B

在点A，鱼的尾尖向下运动，接近幅度的谷值，而且此时尾尖是在减速的，在改变方向之前是趋于停止的。此刻尾尖处形成顺时针方向的涡，鱼体下表面有逆时针方向的涡脱落。而且在鱼尾后方有相反方向涡的破坏性结合［16］，形成了新的逆时针方向的涡，所以阻力减小很多。

在点B，鱼的尾尖向上运动接近中线的位置，而且尾尖的速度接近于最大值。此刻鱼体头部上表面有顺时针方向的涡形成。由于鱼的运动，在A点时结合形成的逆时针方向的涡继续向下游运动。同时可以看到，尾尖处不同方向的涡相遇开始产生破坏性的作用，由于还未形成新的涡，所以阻力较A点增加。

3 结 论

本文通过对鱼摆动的一些基本参数的研究，分析了其对推进力的影响，得到以下结论：

（1）对于各种模式下鱼的摆动，产生推进力时都存在一个临界频率、临界波长和临界雷诺数。通过参数分析，可知在鱼体摆动幅度保持不变的情况下，增大频率、增大波长、增大雷诺数均可使鱼的推进力增大，而相应的临界值也会减小。

（2）鱼体中线是以行波的模式振动的。研究表明，鱼的形状不同，产生的推进力也不同。厚度越大，推进力越小。弯度对推进力影响较小。

（3）鱼产生的推进力与鱼尾尖的位置以及涡有关。尾尖在不同位置，尾尖的速度不同，因而鱼表面涡的分布和强度不同，导致推进力的变化。

［1］LIGHTHILL M J.Note on the swimming of slender fish［J］.JournalofFluidMechanics，1960，9（2）：305－317.doi：10.1017／S0022112060001110

［2］NEWMAN J N.The force on a slender fish－like body［J］.Jour－nalofFluidMechanics，1973，58（4）：689－702.doi：10.1017／S0022112073002429

［3］TONG B G，ZHUANG L X.Hydrodynamic model for fish＇s undulatory motion and its applications［J］.ChineseJournalof Nature，1998，20（1）：1－7.（in Chinese）童秉纲，庄礼贤.描述鱼类波状游动的流体力学模型及其应用［J］.自然杂志，1998，20（1）：1－7.

［4］LIU H，WASSERSUG R，KAWACHI K.A computational fluid dynamics study of tadpole swimming［J］.TheJournalof ExpermentalBiology，1996，199：1245－1260.

［5］PESKIN C S.Numerical analysis of blood flow in the heart［J］.JournalofComputationalPhysics，1977，25（3）：220－252.doi：10.1016／0021－9991（77）90100－0

［6］CHEN H.Volumetric formulation of the lattice Boltzmann method for fluid dynamics：Basic concept［J］.PhysicalReviewE，1998，58（3）：3955－3963.doi：10.1103／PhysRevE.58.3955

［7］INAMURO T，OGATA T，TAJIMA S，et al.A lattice Boltzmann method for incompressible two－phase flows with large density differences［J］.JournalofComputationalPhysics，2004，198（2）：628－644.doi：10.1016／j.jcp.2004.01.019

［8］LALLEMAND P，LUO L S.Theory of the Lattice Boltzmann method：Dispersion，dissipation，isotropy，Galilean invariance，and stability［J］.PhysicalReviewE，2000，61（6）：6546－6562.doi：10.1103／PhysRevE.61.6546

［9］LEE T，LIN C L.A stable discretization of the lattice Boltzmann equation for simulation of incompressible two－phase flows at high density ratio［J］.JournalofComputationalPhysics，2005，206（1）：16－47.doi：10.1016／j.jcp.2004.12.001

［10］SHU C，LIU N，CHEW Y T，et al.Numerical simulation of fish motion by using lattice Boltzmann－immersed boundary velocity correction method［J］.JournalofMechanicalScience andTechnology，2007，21（9）：1352－1358.doi：10.1007／BF03177420

［11］SHU C，LIU N，CHEW Y T.A novel immersed boundary velocity correction－lattice Boltzmann method and its application to simulate flow past a circular cylinder［J］.JournalofComputationalPhysics，2007，226（2）：1607－1622.doi：10.1016／j.jcp.2007.06.002

［12］VIDELER J J.Fish swimming［M］.London：Chapman ＆Hall，1993.

［13］SHU C，NIU X D，CHEW Y T.Taylor series expansion and least squares－based lattice Boltzmann method：three－dimensional formulation and its applications［J］.InternationalJournalof ModernPhysicsC，2003，14（7）：925－944.doi：10.1142／S0129183103005133

［14］ZHU Q，WOLFGANG M J，YUE D K P，et al.Three－dimensional flow structures and vorticity control in fish－like swimming［J］.JournalofFluidMechanics，2002，468：1－28.doi：10.1017／S002211200200143X

［15］BARRETT D S，TRIANTAFYLLOU M S，YUE D K P，et al.Drag reduction in fish－like locomotion［J］.JournalofFluid Mechanics，1999，392：183－212.doi：10.1017／S0022112099005455

［16］WU J，SHU C.Numerical study of flow characteristics behind a stationary circular cylinder with a flapping plate［J］.Physicsof Fluids，2011，23（7）：073601.doi：10.1063／1.3601484