GM(1，1)和趋势外推模型在我国艾滋病发病率预测中的应用*

杨永利 毛赛彩 薛 源 田翔宇 施学忠△

艾滋病是当今世界各国共同关注的一个公共卫生问题，根据2012年第十九届国际艾滋病大会的疫情公告，全世界共有3400万人感染了艾滋病毒或艾滋病，绝大多数在低收入和中等收入国家；艾滋病已成为全世界头号传染病杀手，迄今已造成3000多万人死亡[1]。在我国，艾滋病疫情已波及全国31个省，且其疫情有不断扩大的趋势。艾滋病在我国流行广、发病率和病死率高，严重危害人民的生命和健康，属于重点防治的传染病之一。监测和预测是艾滋病流行病学研究中重要组成部分，它对了解人群中艾滋病发病和死亡情况，制定艾滋病防控措施有重要意义。目前，用于艾滋病疫情预测的模型有GM(1，1)、神经网络模型和时间序列模型[2-3]等。但由于艾滋病流行因素的复杂性，加上不同的预测模型有不同的预测思想和预测理论，不同的预测模型用于同一艾滋病疫情数据时，效果也不相同，因此需综合比较多种模型的拟合和预测效果[4]。该研究采用GM(1，1)和趋势外推模型进行拟合2000-2011年期间我国艾滋病发病率，探讨GM(1，1)和趋势外推模型在我国艾滋病发病率预测中的可行性，选择最优模型预测我国未来艾滋病的发病趋势并用2012年的数据进行回代验证，为艾滋病防控工作提供科学依据。

数据来源和方法

1.数据来源

2000-2011年我国艾滋病发病率资料来自中华人民共和国卫生部网站http://www.moh.gov.cn的中国卫生统计年鉴，2012年艾滋病发病率资料来自中国性病艾滋病协会网站http://www.aids.org.cn。

2.模型介绍

GM(1，1)由一个单变量的一阶微分方程构成，其方程为：

式中，xt为原始时间序列，α为发展系数，u为灰色作用量。

模型的预测精度分为4个等级，见表1。模型最后的精度级别为C和P两个指标中较低的级别。当模型的精度级别达到3级或更高，方能用于外推预测。

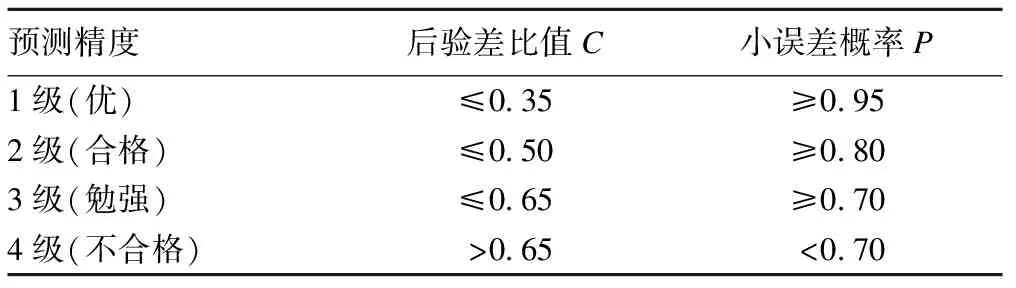
表1 GM(1,1)预测精度等级判定

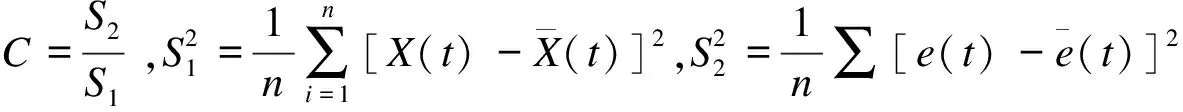
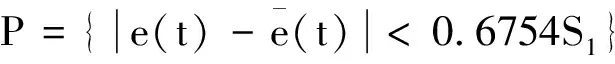
2. 趋势外推模型

趋势外推的基本假设是未来系过去和现在连续发展的结果，它通过一个合适的函数曲线反映它们之间的规律性联系，作为预测未来的依据。趋势外推模型有一次、二次、三次回归模型、指数曲线预测模型、对数曲线预测模型、生长曲线预测模型以及复合曲线预测模型等[5]。实际应用中，可依据图形识别法进行模型的初筛，最后依据决定系数越大，标准误差越小的原则来确定选用哪种趋势外推模型。

3.模型拟合效果评价

采用平均误差率(mean error rate，MER)及决定系数(R2)两个指标来评价GM(1，1)模型和趋势外推模型对我国艾滋病发病率资料的拟合精度[6]。MER越小，R2越大，说明模型拟合精度越高；选择拟合精度高的模型用于预测。

MER=平均误差绝对值/实际值的均值×100%

R2=(SS实-SS残)/SS实

式中，SS实表示实际的方差，SS残表示残差的方差。

4.模型预测效果评价

采用相对预测误差[7]评价模型的预测效果，相对预测误差越小说明预测结果越准确。

5.统计学软件

采用SPSS 13.0进行趋势外推法，采用excel拟合GM(1，1)模型。

结 果

1.GM(1,1)拟合和回代结果

表2 我国艾滋病发病率的GM(1,1)计算过程

后验差比值C=0.271，小误差概率P=0.818，综合起来该模型精度处于合格等级，可以用于我国艾滋病发病率的预测。

D=429.599,α=-0.247,u=0.143

2.趋势外推模型拟合结果

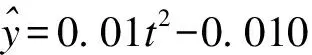
3.GM(1,1)和二次曲线回归模型拟合效果对比

GM(1,1)和二次曲线回归模型的MER分别为28.6%和7.6%，决定系数分别为0.800和 0.990，说明二次曲线回归模型对我国艾滋病发病率的拟合效果优于GM(1,1)。

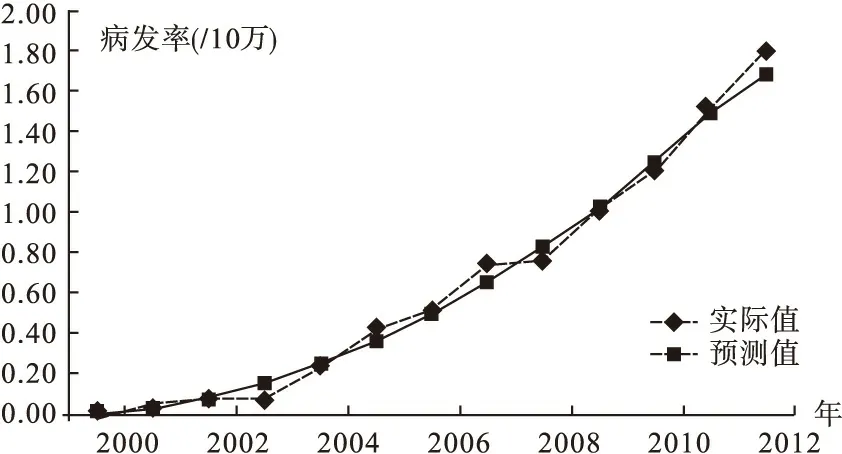
图1 我国艾滋病实际发病率和二次曲线回归模型预测的发病率

4.我国艾滋病发病率预测

讨 论

根据历年艾滋病疫情数据，采用合适的数学模型预测艾滋病的发病水平，一方面可以为制定有效的防制措施提供科学依据，从而使艾滋病预防控制工作更具针对性、预见性和主动性，达到防止暴发或流行的目的；另一方面，也可以将实时疫情信息与同期历史资料比较，对于发病率超出所确定可信限范围者作为异常来处理，以此发出暴发或流行的警示，从而实现疾病的早期预警的作用等。该研究比较了GM(1，1)和趋势外推模型在我国艾滋病发病率拟合中的效果，筛选出拟合效果较好的模型进行预测。

GM(1，1)是一种单变量一阶微分方程，因其计算简单，对样本含量和概率的分布没有严格要求，对数据的分布没有特殊要求[8]而具有较强的实用性，已经被用于多种传染病的预测中[9]。趋势外推模型属于因果关系模型，它从一个指标与其他指标的历史和现实变化的相互关系中，探索它们之间的规律性，通过拟合回归方程，来对事物未来的发展趋势进行预测。该研究采用GM(1，1)和趋势外推模型，分别拟合了我国艾滋病发病率，结果显示，GM(1，1)后验差比值为0.271，小误差概率为0.818，拟合精度为合格等级，说明GM(1，1)可以用于我国艾滋病发病率的拟合中。趋势外推模型中的二次曲线回归模型也可用于我国艾滋病发病率的拟合中。但是对比这两种模型的拟合结果，二次曲线回归模型的拟合精度更高，其平均误差率为7.6%，决定系数为0.990。决定系数高，一方面意味着二次曲线回归模型在揭示过去我国艾滋病发病率变化规律方面与实际情况高度吻合，理论上可以较准确地预测我国艾滋病发病率；另一方面也反映了影响我国艾滋病发病的生物因素、社会因素、政策因素等比较平稳，因此艾滋病的发病规律容易被揭示和预测。根据二次曲线回归模型，预测2012，2013和2014年，我国艾滋病发病率分别为1.68/10万，1.95/10万和2.24/10万，2012年发病率数据的回代验证显示二次曲线回归模型预测效果理想，预测的相对误差仅6.14%，说明二次曲线回归模型不仅可用于我国艾滋病发病率的拟合，也可用于艾滋病疫情的预测。该研究显示，未来几年，我国艾滋病的发病水平仍将呈现上升趋势，艾滋病的流行对中国仍将是个持续性的挑战，为了阻止艾滋病的流行，亟需将HIV/AIDS防治纳入到卫生保健和公共卫生规划的常规工作，加强多部门之间的合作[10]。

该研究显示趋势外推模型中的二次曲线回归模型更适合我国艾滋病发病率的拟合和预测，这对正确指导公共卫生人员依据疫情预测提前做好防控工作，制定有效防控策略有重大意义。但我们还应意识到，艾滋病疫情演变过程中会受到诸多因素的影响，使得原有模型的预测效能降低，因此建立的预测模型并不是固定不变的，需不断补充最新的数据后再探讨最合适的模型。

参 考 文 献

1.Flaskerud JH.AIDS 2012: Goals and accomplishments,the XIX international conference .Issues Ment Health Nurs，2013，34(5):380-382.

2.Liu Q， Liu X， Jiang B， et al.Forecasting incidence of hemorrhagic fever with renal syndrome in China using ARIMA model .BMC Infect Dis,2011,11(8):218-224.

3.谢妮.深圳市HIV/AIDS疫情分布特征与预测模型比较D.中南大学博士学位论文,2011:60-61.

4.范引光，吕金伟，戴色莺，等.ARIMA模型和灰色预测模型GM(1,1)在HIV感染人数预测中的应用.中华疾病控制杂志，2012，16(12):1100-1103.

5.薛薇.SPSS统计分析方法与应用(第2版).北京:电子工业出版社,2010:276.

6.梁会营，李雪莲，郭军巧，等.3 种模型在肾综合征出血热发病率拟合预测中的比较研究.中国医科大学学报，2008，37(6)：843-846.

7.朱奕奕，赵琦，冯玮，等.应用指数平滑法预测上海市甲型病毒性肝炎发病趋势.中国卫生统计,2013，30(1):31-33,36.

8.Geskus RB.Cause-specific cumulative incidence estimation and the fine and gray model under both left truncation and right censoring .Biometrics，2011，67(1)：39-49.

9.王平，路金星.应用灰色模型预测甲乙类肠道传染病发病趋势.浙江预防医学，2010，22(8)：24-26.

10.Zhang KL， Detels R， Liao St， et al.China’s HIV/AIDS epidemic：continuing challenges .Lancet，2008，372(9652)：1791-1793.