应用logistic回归模型间接估计RR/PR的方法探讨*

广东药学院公共卫生学院流行病与卫生统计学系(510310) 李鹏声 梁 融 周舒冬 郜艳晖 杨 翌

流行病学暴露与结局的关联性研究中，当结局事件发生率较为罕见(如小于10%)时，OR(odds ratio，优势比)近似等于RR(relative risk，相对危险度)或PR(prevalence ratio，患病率比)，且通过logistic回归可方便地获得OR及其置信区间，因此实际工作中常使用OR描述暴露与结局的关联强度。但当研究结局发生率较高(如大于10%)时，使用OR会严重地高估RR/PR。这一问题近年来已引起学者关注并指出横断面研究中宜估计PR、队列研究中宜估计RR以描述暴露与结局的关联强度[1-2]，同时也发展了直接估计RR/PR的方法，如修正的Cox比例风险模型[3]、稳健Poisson回归[4]和log-binomial[5]回归等。但由于logistic回归更被流行病学者所熟识，本文探讨使用logistic回归来间接估计RR/PR的方法，为统计方法的选择提供参考。

原理和方法

根据RR/PR的定义，可直接利用logistic回归模型中预测概率的比值估计[6]：

(1)

式(1)中Y表示结局变量，E表示研究的暴露因素，x2,…,xp表示各种协变量。值得注意的是，使用式(1)估计RR/PR取决于模型中协变量的取值，根据其取值的不同，可分为三种方法[7]。

1.条件(conditional)法

在条件法中，指定一个参考值作为式(1)中协变量的取值，如取协变量的均值，因此RR/PR为协变量均值条件下的估计，即：

(2)

2.边际(marginal)法

边际法无需指定参考值，而使用每个观察个体自身的协变量取值，分别计算当所有观察对象均为暴露组与均为非暴露组时预测概率的平均值，相除得到边际RR/PR，即：

(3)

3.分层(stratified)法

分层法类似直接标化法，选取一个标准人口，依据标准人口中协变量分段将研究人群分成k层，采用标准人口中各层的协变量构成作为权重Wk，同一层的研究对象协变量取值相同，通常取其均值，再计算RR/PR，即：

(4)

上述三种方法的置信区间(confidence interval，CI)都可用Bootstrap方法来估计。Bootstrap方法的基本原理是对原始样本进行B次有放回的重抽样，从B个Bootstrap子样本中产生B个统计量的观察值，从而得到参数的经验分布，然后进行参数估计。常用的Bootstrap估计CI方法有三种[8]，其中t分布法假设用Bootstrap子样本求出的RR/PR服从正态分布且各个观察值之间相互独立，精确率较高；百分位数法属于非参数法，对RR/PR的分布没有要求，但精确度不如t分布法；偏差校正百分位数法则在百分位数法的基础上校正了原始样本的RR/PR与Bootstrap子样本RR/PR中位数的偏差，提高了精确度。Bootstrap方法在SAS统计软件中可通过PROC SURVEYSELECT过程来实现，将METHOD语句指定为URS即可。

实例分析

实例来自2009年“广州市禁烟立法基线调查”资料。本研究选取男性人群资料，研究男性人群中吸烟与禁烟立法态度间的关联，并考虑年龄的混杂效应。在接受调查的2129例男性居民中，不赞成禁烟立法的比例为17.72%(>10%)，其中吸烟者的不赞成率为30.27%，高于不吸烟者(9.39%)，粗PR=3.224。吸烟情况及各年龄层居民的不赞成率见表1。

表1 男性吸烟情况、年龄与禁烟立法态度的频数分布

考虑到年龄可能是吸烟与禁烟立法态度关联的混杂因素，估计PR时将其作为协变量纳入logistic回归模型，再分别运用三种方法估计PR，在条件法中，以调查对象年龄的均值(41.48岁)作为式(2)中年龄变量的取值。在边际法中，将每个调查对象的年龄代入式(3)，而在分层法中，本文选取广州市第六次人口普查(2010年)数据[9]作为标准人口，以每层人数占总人口的比例作为权重Wk，取每层研究对象年龄的均值(各层分别为17.00、24.48、34.87、44.50、54.58、64.38、74.25、82.40、93.33岁)代入式(4)计算PR。经三种方法得到PR后，均用Bootstrap方法估计PR的95% CI。经正态性检验，PR的经验分布均不服从正态分布(P<0.05)，因此使用偏差校正百分位数法，各方法估计结果见表2。

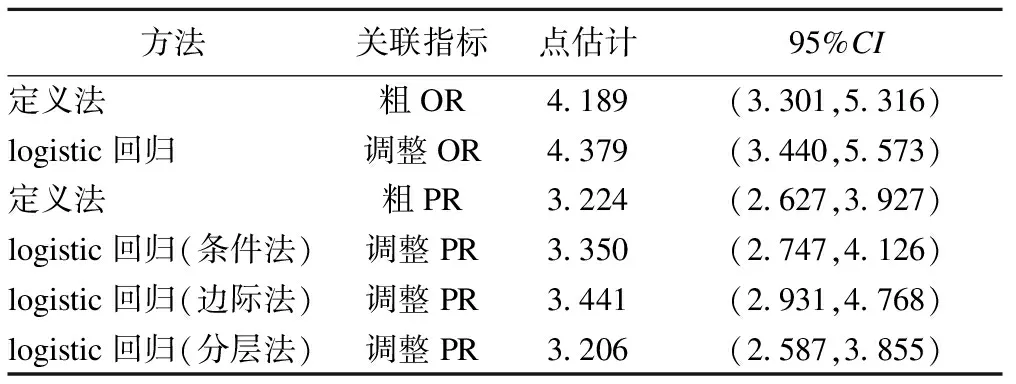
表2 用不同方法估计吸烟与禁烟立法态度的关联强度指标

可以看到，在条件法、边际法和分层法中，男性吸烟者禁烟立法不赞成率分别是不吸烟者的3.350 (95%CI: 2.747,4.126)倍、3.441 (95%CI: 2.931,4.768)倍和3.206 (95%CI: 2.587,3.855)倍。而OR则高估了吸烟与禁烟态度的关联，为4.379(95%CI: 3.440,5.573)，说明在患病率高的情况下(本例男性不赞成率为17.72%)，使用OR会高估关联的程度。本例调整年龄后的OR和PR与粗OR和PR相差不大，表明年龄在此处的混杂作用不强。

讨 论

当所研究的结局在人群中的患病率较高(>10%)时，使用OR会导致高估暴露与结局的关联强度。因此在横断面研究中宜使用PR、队列研究中宜使用RR以描述暴露与结局的关联强度。相比其他直接估计RR/PR的方法，如Poisson回归，log-binomial回归等，使用logistic回归来间接估计RR/PR具有以下优点：①Logistic回归使用广泛，被广大研究人员尤其是非统计专业研究人员所熟识，易于使用和推广；②与直接用定义式计算RR/PR相比，可以控制协变量，与使用Mantel-Haenszel法相比，可以控制多个协变量，且适用于连续型协变量；③流行病学研究中层次结构数据普遍存在，基于logistic回归的多水平模型理论成熟，应用广泛，当研究非稀有结局时，本文介绍的方法可直接推广到多水平模型用于估计RR/PR，且其置信区间也可通过Bootstrap方法得到。

本文介绍了基于logistic回归间接估计RR/PR的三种方法，实际应用中，将协变量指定为某一参考值的条件法是最为简便的一种选择，此外，在条件法中通过指定不同的参考值，可比较在协变量不同水平下的RR/PR[10]。当研究目的是比较样本中所有个体均为暴露组时与均为非暴露组时的风险，则选用边际法更为恰当。当不同暴露组之间协变量的分布不同时，可考虑使用分层法。分层法的基本思想类似直接标准化法，利用标准人口的协变量分布作为权重，来调整该协变量的分布，使各组间均衡可比。本文考虑年龄作为协变量，实际应用中，协变量为其他因素时或多因素时，选择标准人口的协变量或多变量联合分布可能较为困难。

本文实例中只考虑了一个协变量，在需要同时控制多个协变量的情况下，条件法或边际法只需要在公式中加入不同的协变量即可。对于分层法则较为复杂，随着协变量分层数或需要调整的协变量数增多，需要计算的权重也随之增加，而且在样本量较小的情况下，可能会出现某些层的观察对象数目过少甚至没有的情况，导致无法分层调整。对于这些情况，可以考虑使用聚类分析来控制分层的数目[11]，或者用倾向评分加权来调整权重[12]。

参 考 文 献

1.Lee J,Chia KS.Use of the prevalence ratio v the prevalence odds ratio as a measure of risk in cross sectional studies.Occup Environ Med,1994,51(12):841.

2.Zhang J,Kai FY.What’s the relative risk?JAMA: the journal of the American Medical Association,1998,280(19):1690-1691.

3.Barros AJ,Hirakata VN.Alternatives for logistic regression in cross-sectional studies: an empirical comparison of models that directly estimate the prevalence ratio.BMC Med Res Methodol,2003,3:21.

4.童峰,陈坤.常见结局事件的前瞻性研究中修正Poisson回归模型的应用.中国卫生统计,2006,23(5):410-412.

5.叶荣，郜艳晖，杨翌，等.log-binomial模型估计的患病比及其应用.中华流行病学杂志，2010，31(5):576-578.

6.Mcnutt LA,Wu C,Xue X,et al.Estimating the relative risk in cohort studies and clinical trials of common outcomes.Am J Epidemiol,2003,157(10):940-943.

7.Santos CA,Fiaccone RL,Oliveira NF,et al.Estimating adjusted prevalence ratio in clustered cross-sectional epidemiological data.BMC Med Res Methodol,2008,8:80.

8.Efron B,Tibshirani RJ.An introduction to the bootstrap.New York: Champan & Hill,1993:153-199.

9.广州市人口普查办公室编.广州市2010年人口普查资料.北京:中国统计出版社,2012.

10.Localio AR,Margolis DJ,Berlin JA.Relative risks and confidence intervals were easily computed indirectly from multivariable logistic regression.J Clin Epidemiol,2007,60(9):874-882.

11.张吉凯,胡毅玲,胡巢凤,等.聚类在流行病学分层分析中的应用.中华流行病学杂志,2003,24(7):615-617.

12.李智文,刘建蒙,任爱国,等.基于个体的标准化法-倾向评分加权.中华流行病学杂志,2010,31(2):223-226.