基于NSCT域邻域收缩的SAR图像去噪

钟微宇, 沈汀

ZHONG Weiyu1,2, SHEN Ting 2

1.中国科学院研究生院，北京 100049

2.中国科学院对地观测与数字地球科学中心，北京 100094

1.Graduate University of Chinese Academy of Sciences, Beijing 100049,China

2.Center for Earth Observation And Digital Earth, Chinese Academy of Sciences, Beijing 100094, China

1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)是一种主动式微波遥感器, 可以全天时、全天候成像,在军事和民用方面发挥着越来越巨大的作用。SAR的成像机理致使SAR图像存在固有的相干斑噪声，这将非常不利于 SAR图像中景物的自动解译，特别是噪声较强时，图像中点目标、边缘轮廓和纹理细节将被噪声淹没。因此SAR图像中的相干斑噪声的去除是 SAR图像处理中急需解决的一个关键问题。去噪效果的好坏直接影响到SAR图像的后续处理，如分割、目标检测等。

近年来，SAR图像相干斑噪声抑制技术得到飞速发展，主要分为两大类:空域滤波和频域滤波。空域滤波有Lee[1]、Gamma_MAP[2]等，这些滤波方法在一定程度上可以有效地减弱噪声的影响，但此类滤波方法往往会对图像产生过平滑作用，使图像变模糊，细节信息丢失严重。频域滤波有基于小波变换[3]的去噪方法和基于多尺度几何变换的去噪方法[4]。小波变换具有时频局部化特性,它可以从不同的分辨率空间来描述图像的局部特征，但对于具有线状奇异的目标函数（如图像的边缘），小波系数不再稀疏。因此小波变换在SAR图像去噪中并不能够很好地保持图像中的边缘轮廓细节信息，其根本原因在于小波分析在二维空间并不是最优的函数表示方法，并不能很好地刻画图像中具有线奇异的几何信息。针对小波变换的不足，2006年，Cunhua等人提出了一种新的多尺度几何分析工具-非下采样轮廓变换(NSCT)[5]，用于SAR图像去噪具有明显优势。NSCT通过构造轮廓基来检测小波基所不能充分刻画的几何结构，同时很好地保持了图像的奇异信息，有利于增强去噪结果中细节结构的保持能力。NSCT继承了小波变换的时频特性，同时具有良好的多方向性、各向异性和平移不变性。

2005年，A.Krzyzak[6]等人提出了基于小波域邻域收缩（NeighShrink）的去噪方法。该去噪方法利用小波系数相关性，使用邻域收缩法对小波系数进行处理，取得较好去噪效果。后来出现各种改进的NeighShrink去噪方法。2008年，周登文[7]等人针对NeighShrink在各个小波子带上均使用次优的阈值以及固定的邻域窗口尺问题，运用 Stein的无偏风险估计改进NeighShrink方法。2010年，宫霄霖[8]提出了基于相关度分析的自适应邻域小波去噪算法，来解决 NeighShrink不能自动选取合适邻域窗口大小的问题。2011年，武海洋[9]等人则采用静态小波变换域中NeighShrink方法,以此来克服正交小波变换域使用全局阈值不能反映小波系数随尺度变化的不足。上述的这些去噪方法都是在小波域中使用 NeighShrink方法，然而小波变换不具有多方向性、各向异性和平移不变性，致使在小波域使用NeighShrink去噪不能较好地保护纹理细节信息。本文将借鉴邻域收缩的方法，提出一种基于NSCT域邻域收缩的 SAR图像去噪方法。该法利用 NSCT系数的相关性，使用 NeighShrink对不同子带系数进行收缩，以提高去噪性能和较好地保护边缘信息。真实SAR图像的仿真实验证明了本算法的有效性。

2 基于NSCT域邻域收缩的SAR图像去噪

2.1 非下采样轮廓变换（NSCT）的基本原理

非下采样轮廓变换（NSCT）是一种利用迭代非下采样滤波器组来实现一系列多分辨率、多方向和平移不变的频域子图像的算法。该算法先将图像进行多尺度分析，然后再进行多方向分析，两步分开进行逐层迭代。NSCT的结构为非下采样金字塔滤波器组(Nonsubsampled Pyramid Filter Bank ，NSPFB)和非下采样方向滤波器组(Nonsubsampled Directinnal Filter Bank，NSDFB)两部分，其实现结构原理如图1所示,其中图1(a)为NSCT的结构图(黄色表示通带，灰色表示阻带)，图1(b)为NSCT非下采样塔形分解和非下采样方向滤波的频率分割示意图。其分解过程可表述为：先利用非下采样塔式滤波器组（NSPFB）对图像进行多尺度的分解，得到各种不同频率的高频子带图像和一个低频子带图像，然后再利用非下采样方向滤波器组（NSDFB）对得到的各高频子带图像进行多方向分解，从而得到不同尺度、不同方向的子带图像（系数）。

图1 实现NSCT的结构原理图

2.1.1 非下采样塔式滤波器组（NSPFB）

NSCT的多尺度特性是通过二通道非下采样滤波器组(NSPFB)分解获取的。NSPFB能够达到类似于 LP的子带分解结构，第l层分解的低通滤波器的理想带通支撑为[-p/2l,p/2l]2，相应高通滤波器 H1(z)的理想支撑应为[-π/2l-2,π/2l-1]2[-π/2l,π/2l]2，是低通滤波器的补集。NSCT采用的NSPFB为二通道非下采样滤波器组，如图2所示, 分解滤波器{H0(z), H1(z)}和合成滤波器{G0(z), G1(z)}满足Bezout恒等式：

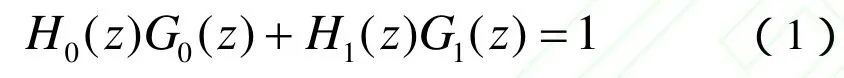
（1）式保证了 NSPFB满足完全重构（Perfect Reconstruction,PR）条件。其中，NSPFB的实现去除了 LP的下采样操作，并对滤波器进行相应的插零上采样来完成的。当NSPFB分解层数为L时，经分解得到 1个低通子带图像和 L个高通子带图像，由于没有下采样，所有子带图像与原始图像尺寸相同。非下采样塔式滤波器组的三级分解原理图如图3所示，将图像分为一个低频子图（Y0）和三个高频子图（Y1、Y2、Y3）。

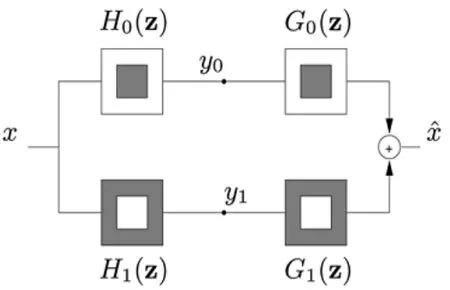
图2 NSPFB

图3 非下采样塔式滤波器组分解图

2.1.2 非下采样方向滤波器组（NSDFB）

NSCT采用的 NSDFB也是一组二通道非下采样滤波器组，来实现频域方向分解，如图4所示。其中分解滤波器{U0(z), U1(z)}和合成滤波器{V0(z), V1(z)}也满足Bezout恒等式：

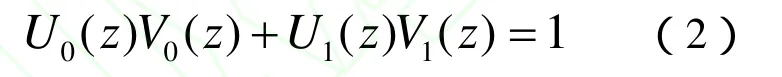
（2）式保证NSDFB满足完全重构条件。NSDFB实现过程是先对滤波器U0(z)和U1(z)进行上采样，再对上一级二通道方向分解后的子带图像进行滤波，从而实现频域中更为精确的方向分解。某尺度子带图像经过l级方向分解后，就得到了2l个与原图像尺寸大小相同的方向子带图像。实现四通道方向NSDFB分解图如图5所示。

图4 NSDFB

图5 扇形滤波器实现四方向分解示意图

将 NSPFB与 NSDFB相结合，就可以实现NSCT。原图像经NSPFB分解后得到的带通子带图像，再输入到 NSDFB中可获得图像的带通方向信息，从而实现对图像的多尺度、多方向分解。

设输入图像为 f(x, y),大小为M*N，NSCT对图像的分解过程可由式(3)所示：

其中aJ为低频子带，bj,k为j尺度,k方向的高频子带。一个NSCT低频系数可用aJ(m, n)表示，一个NSCT高频系数可用 bj,k(m, n)表示。其中J为NSPFB的分解层次；lj为第j层的NSDFB的分解层次；j表示 NSPFB分解后的尺度标号；k表示NSDFB中方向标号；m、n表示系数在方向子带中的空间位置。图6给出了一幅图像（zoneplate）的NSCT一层二方向的分解示意图，金字塔分解为1级，方向滤波数为2。

图6 zoneplate图像的NSCT例图

2.2 邻域收缩法的原理

针对阈值去噪法对于许多可能包含有用细节信息的变换系数的“过扼杀”（如硬阈值）[10],或是对于噪声“过保留”（SURE阈值）[11]的问题,文献[6]提出一种新的去噪方法-邻域收缩法(NeighShrink)。邻域收缩法的思想是假定在一个变换域中，在一个较小的系数邻域内，变换系数具有一定的相关性，即在幅值较大的系数周围存在较大的系数的概率非常大，所以在对噪声进行阈值处理时，可以参考邻域系数的情况，利用尺度内系数相关性。在估计无噪声变换系数时考虑当前系数邻域系数的分布情况，而不在是孤立地看待每个系数，如图7所示。

图7 邻域收缩系数图

NeighShrink去噪算法可由以下几个步骤来描述：

1）.对含噪图像进行某种变换，如小波或多尺度几何变换，将图像分解为不同频率的子带图像。

2）.对于分解得到 j尺度,k方向的高频子带系数 bj,k(m, n)，计算出以(m, n)为中心的窗口内所有系数的平方和，即：

其中，W是以（m,n）为中心的窗口;

3）.计算收缩阈值：

其中 M*N为图像的大小，σj,k表示图像j尺度,k方向的高频子带的噪声标准差；

4）.确定收缩因子 βj,k(m, n):

5）.进行系数收缩。收缩后的系数为：

6）.最后对修改后的系数进行相应的逆变换，得到去噪后的图像。

2.3 结合邻域收缩的NSCT域SAR图像去噪算法实现

文献[5]中 NSCT去噪方法采用硬阈值，对NSCT变换的全部系数采用同一个阈值，通过设定阈值，然后比较系数和阈值，小于阈值的系数将其置为 0。但该法把一部分代表纹理细节信息的系数也置零，导致过度扼杀系数，造成了伪影和模糊。文献[6]在小波域使用 NeighShrink也有局限性，这是由于小波变换的方向有限，不具有平移不变性。对此，本文将利用NSCT的多方向性、各向异性和平移不变特性，在NSCT域使用NeighShrink处理含噪的变换系数。本文对一幅 river图像(图 9(p1))经对数变换后，再进行NSCT分解，分解层数为3，每层方向为 4，4，8，对第二、三层的各一个方向的子带进行直方图统计，如图8(a)和图 8(b)所示。从直方图中可看出，图像经NSCT分解后，其系数往往呈现稀疏性分布：大部分变换系数的幅值较小，它们对应图像中的光滑部分或白噪声；只有小部分的幅值较大，这些系数含有一些重要的信息，如图像的边缘或奇异位置。在图像的其他子带中，也可观察到类似的分布。

图8 river SAR图像NSCT的系数统计直方图

D.D.Po[4]等人根据邻域的相关熵理论对轮廓系数的尺度间、尺度内和方向间的相关性进行了详细分析，并得出结论：轮廓系数在尺度间、尺度内和方向间都存在较强的相关性，其中尺度内变换系数的相关性最强；并将轮廓系数尺度间的相关性与小波系数尺度间的相关性进行了比较，得出前者比后者有更强的相关性。文献[12]依据轮廓系数尺度间的相关性，提出一种基于双变量阈值的NSCT图像去噪方法，实验结果表明，去噪图在边缘特征方面保持了良好的视觉效果。本文则利用 SAR图像经NSCT分解后，其系数在邻域内有较强的相关性，提出一种基于NSCT域的邻域收缩去噪方法。根据邻域窗口内所有NSCT系数的平方和的大小来决定处于该窗口中心的NSCT系数是收缩还是置零。对少量幅值较大的系数，由尺度内的相关性可得其窗口内平方和较大，由公式6对其进行收缩处理；而对大量幅值较小的系数，当窗口内平方和很小时，对窗口中心系数进行置零处理。相对于软硬值去噪方法而言，该法由于考虑它们邻域系数的分布情况，这样能减少重要的变换系数被误置为零的情况，可以尽量多地保留图像细节。

基于 NSCT域邻域收缩的 SAR图像去噪算法的步骤由下：

(1).对原始 SAR图像进行对数变换，把服从Gamma分布的乘性噪声转换成加性高斯噪声。

(2).按照实验中的 NSCT分解层数和方向分解层数，对经对数变换后的 SAR图像进行 NSCT分解，得到低频子带和高频子带图像（系数）；

(3).由于低频子带图像aJ含有部分噪声，为更好地平滑噪声，将用中值滤波去除这部分噪声，设去噪后的低频子带图像为；

(4).使用鲁棒的中值估计子[13]估计不同子带系数的噪声标准差σj,k，即

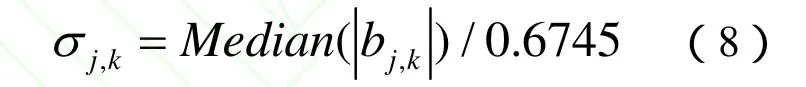
再由式(5)计算 j尺度,k方向的高频子带收缩阈值Tj,k。其中Median表示取中值运算，定义为对变换系数按大小排列，再取中位数；

(5).使用式(6)和式(7)对高频子带系数进行收缩去噪处理，以估计无噪声高频系数；

3 实验及分析

为验证本文去噪算法的有效性，将选取边缘等细节信息比较丰富，具有一定代表性的真实 SAR图像进行仿真实验。本文采用二幅SAR图像来进行验证，如图9所示。使用不同去噪算法对这两幅图像进行去噪，最后对去噪结果作对比。两幅图像的灰度级都是 256，其中第一幅图像（river）大小为376×376像素，该成像区域主要有河流和陆地这两部分；第二幅图像(horsetrack)大小为384×384(美国新墨西哥地区，ku波段1M分辨率)，该区域主要有农作物、草地和光滑地表，这幅图像可从网站[14]下载。将本去噪算法与小波软阈值去噪算法[15]、小波邻域收缩去噪算法[10]、NSCT硬阈值去噪算法[5]用于同一幅SAR图像去噪，再比较SAR图像去噪性能量化评估指标。SAR图像去噪性能量化评估指标[16]采用均值(MEAN)、标准差(STD)、等效视数（ENL）、均值保持指数（PM）、相干斑抑制指数（F）这五个参数，来判断去噪算法的优劣。

图9 实验的二幅原始SAR图像

在本文去噪算法的实验参数选择方面，塔式滤波器组选用‘dmaxflat7'，方向滤波器组选用‘maxflat'；塔式滤波器组采用三层分解[17]，方向滤波器组的分解层数为[2 3 3]。中值滤波器[18]的常用窗口大小有5×5和3×3，经实验分析，其窗口大小选为 5×5，用其对分解得到的低频子带进行滤波。而在邻域收缩法中的窗口大小选择方面，文献[6]实验结果表明 3×3的窗口大小是最优的，当窗口变大时，去噪能力变差，当窗口大小非常小的，去噪能力也不高。因此本文采用 3×3的窗口，这样在噪声抑制和保留纹理细节这两方面能获得较好的折衷。图10和图11为对应于图9(p1)和图9(p2)的不同去噪算法的去噪结果图。

图10 river图像去噪结果图

图11 horsetrack图像去噪结果图

在主观评价方面，从图10（a）和图11（a）中可明显看出，采用小波软阈值去噪算法后，图像中的相干斑受到一定程度的抑制，但图像边缘轮廓被严重模糊，线性特征与相干斑被一起平滑，损失较多的纹理信息，同时去噪后的图像均匀区域出现了一些的吉布斯现象，该法的去噪能力有限。图 10（b）和图11（b）显示小波邻域收缩去噪法对 SAR图像的均匀区域进行了比较好平滑，但图像整体存在模糊失真的现象，图像细节信息丢失比较严重,这是由于小波不是二维图像的最优表示。图 10(c)和图 11(c)表明 NSCT硬阈值去噪算法能较好地去除噪声，但存在比较明显的划痕现象，部分边缘细节也有一定程度的失真。这是由于该法对不同的变换系数采用同一阈值，过度扼杀了一部分代表纹理细节的系数造成的。从以上两图可看出去噪效果还不够明显，在纹理细节保持方面还有待改进。图10(d)和图 11(d)为基于 NSCT域邻域收缩的去噪算法的去噪结果图，平滑区域的噪声去除与以上几种去噪算法相比较为彻底，边缘轮廓清晰锐利，连贯清晰，纹理、边缘（河流线条（图10(d)）、区域分界线（图11(d)））和点目标等细节信息得到较好的保护。本文的去噪算法在图像质量和视觉效果方面相比于以上几种方法均有所改善，提高了图像的平滑性和清晰度。该法良好的去噪效果得益于NSCT具有多分辨率、多方向性的特性和NSCT系数之间的相关性。总之，从图10和图片11可知，在NSCT域中使用邻域收缩法对变换系数进行收缩，能较好地去除SAR图像噪声和保护纹理细节，这将非常有利于后续的图像处理。

在客观评价方面，本文使用等效视数、相干斑抑制指数、均值、标准差、均值保持指数这5个量化指标来评价去噪结果的优劣。表1和表2给出了原始图像及4种去噪算法对SAR图像去噪的量化指标。表1中所得的数据的计算区域（较均匀区域块）大小为90*80，即图9(p1)中黄色标记区域；表2中的计算区域大小为80*60，即图9(p2)中黄色标记区域。

表1 river图像去噪的量化指标

表2 horsetrack 图像去噪的量化指标

在表1和表2中，从均值保持指数可以看出，这4种滤波方法PM值都非常接近于1，即上述4种去噪算法的均值和原图像的均值相差不多，基本上能保持原始图像的灰度强度。这些方法都有良好的图像均值保持能力，各算法差别不大。均值保持好说明图像没有出现光谱信息的畸变，这将有利于图像的后续处理和解释。而在STD、ENL、F这三项指标中，本文的基于NSCT域邻域收缩的去噪算法在这三项指标中有明显优势，其 STD比其它 3种去噪算法的STD小，表明其去噪能力最强；4种去噪算法所得的ENL值均高于原始图像，而用本文算法所得的ENL都比其它3种去噪算法的ENL大（ENL越大，表明图像上的相干斑越弱，可解译性越好）；同时用本文去噪算法得到的 F最大，这表明本文的方法能更好地平滑图像。综合上述量化评判指标和去噪后的图像对比，本文提出的基于NSCT域邻域收缩的去噪算法在去除SAR图像噪声和保护纹理细节方面是有效的。

4 结束语

本文实现了一种基于非下采样轮廓变换（NSCT）域邻域收缩的SAR图像去噪算法，算法首先对受相干斑干扰的SAR图像进行NSCT分解，然后对分解得到的低频子带图采用中值滤波算法，以去除图像中的低频噪声。接着再利用NSCT分解的高频系数之间有较强的相关性的特征，使用邻域收缩法对高频子带图的系数进行收缩，对不同系数使用不同的收缩因子，以提高去噪性能指标和保护纹理细节信息能力。真实SAR图像的去噪实验结果表明，本文的去噪算法能使SAR图像得到较好地平滑，同时兼顾保护纹理细节，使得边缘清晰光滑。该去噪方法具有较好的抗噪性能和良好的边缘细节保留能力，用于SAR图像去噪是有效的，在去噪性能和视觉效果方面相对于上述对比方法均有所提高，为后续的SAR图像处理提供了有效保证。

[1]Lee J S.Refined filtering of image noise using local statistics[J].Computer,Graphics and Image Processing,1981,15(3):380-389.

[2]Barald A, Parmigiani F.A refined Gamma MAP SAR speckle filter with improved geometrical adaptivity[J].IEEE Transactions on Geoscience and Remote Sensing,1995,33(5):1245-1257.

[3]Xie H,Pierce L E and Ulady F T.SAR speckle reduction using wavelet denoising and markov random field modeling[J].IEEE Transactions on Geosciences and Remote Sensing, 2002, 40(10):2196-2212.

[4]Po D D,Do M N.Directional multiscale modeling of images using the Contourlet transform[J].IEEE Transactions on Image Processing, 2006,15(6):1610-1620.

[5]Cunha A L,Zhou J,Do M N.The Nonsubsampled Contourlet Transform:Theory Design,and Applications[J].Transactions on Image Process ing,2006,15(10):3089-3101.

[6]Chen G Y,Bui T D,Krzyzak A.Image denoising using neighboring wavelet coefficients[J].Integrated Computer-Aided Engineering, 2005,12(1):99-107.

[7]周登文,申晓留.邻域小波系数自适应的图像降噪[J].中国图象图形学报,2008,13(11):2112-2116.

[8]宫霄霖.基于小波变换的不规则邻域的数字图像去噪算法研究[D].天津:天津大学，2010.

[9]武海洋,王慧,樊菊.基于静态小波变换改进邻域系数法的遥感图像滤波[J].海洋测绘,2011,31(2):24-27.

[10]Donoho D L, Johnstone I M ,Kerkyacharian G.Wavelet Shrinkage:Asymptopia[J].Journal of Royal Statistics Society,1995,57(4):301-369.

[11]Donoho D L, Johnstone I M.Adapting to Unknown Smoothness Via Wavele Shrinkage[J].J.Acoust.Soc.Am,1995,90(3):1200-1223.

[12]贾建,焦李成,项海林.基于双变量阈值的非下采样Contourlet变换图像去噪[J].电子与信息学报,2009,31(3):532-535.

[13]Chang S G，Bin Y,Varttereli M.Adaptive wavele Thresholding for image denoising and compression[J].IEEE Transaction on Image Processing，2000,9(9),1532-1546.

[14]Horse track near albuquerque,new mexic [EB/OL].[2012-06-8].http://www.sandia.gov/radar/images/horsetrack.jpg.

[15]Donoho D L.Denoising by soft thresholding[J].IEEE Transactions on Information Theory, 1995,41(3):613-627.

[16]王晓军,孙洪,管鲍.SAR图像相干斑抑制滤波性能评价[J].系统工程与电子技术,2004,26(9):1165-1171.

[17]杨晓慧,焦李成.非下采样Contourlet域GCV准则SAR图像去噪[J].计算机应用研究,2009,26(9):3542-3544.

[18]Tukey,J.W.Exploratory Data Analysis.Reading, MA.Addison-Wesley,1977.