模拟退火遗传算法在DOA估计技术中的应用

贾伟娜，刘顺兰

Jia Wei-na，Liu Shun-lan

杭州电子科技大学通信工程学院，浙江 杭州 310018

School of communication Engineering，Hangzhou Dianzi University，Hangzhou Zhejiang 310018，China

1 引言

波达方向（Direction of Arrival，DOA）估计技术利用传感器阵列接收的信号对目标的方位进行估计，其算法的优劣直接影响着 DOA估计的性能。早期的常规 DOA估计方法分辨不出同一个波束宽度内的空间目标。为了提高 DOA估计的分辨率，很多学者对此进行了研究并提出了一系列高分辨DOA估计算法，如MUSIC算法[1]、ESPRIT算法[2]、WSF算法[3]等。其中WSF算法具有思想简单、估计性能优越的特点，尤其是在低信噪比、小快拍数据情况下，该算法比子空间分解算法（如MUSIC、ESPRIT）性能好得多，并且在相干信源情况下仍能有效估计[4]。但WSF算法涉及到非线性多维搜索，真实角度的搜索是非常耗时的。这是该算法在实际应用中遇到的瓶颈问题。为了解决该问题，目前已经提出有交替投影、高斯-牛顿等搜索算法，其中高斯-牛顿算法[3]是一种常用算法，但是这类搜索算法涉及到参数初始值的选取，且初始值选择的好坏直接影响着算法的性能。

遗传算法（Genetic Algorithm，GA）[5]是一种借鉴生物的自然选择和遗传进化机制的全局优化自适应概率搜索算法，适于求解复杂的优化问题，具有很强的鲁棒性。近年来，遗传算法在方位估计中得到了应用。文献[6]在无噪的条件下，通过遗传算法求解信号参数。文献[7]将遗传算法引入到DOA估计中，提出了一种快速DOA估计的新方法—基于最大似然的DOA估计遗传算法。文献[8]将遗传算法应用在目标波束空间 DOA估计中，提出了一种基于宽带目标波束空间DOA估计的新方法。但是基本遗传算法存在局部搜索能力较差和后期搜索迟钝等问题[9]。模拟退火算法（Simulated Annealing，SA）[10]是一种基于热力学退火机理的随机组合优化算法，具有较强的局部寻优能力。若将模拟退火思想应用到遗传算法中去，能克服遗传算法易陷入局部最优的缺点，并使搜索朝着全局最优化方向进行。

本文研究模拟退火遗传算法在 DOA估计技术中的应用，利用模拟退火遗传算法解决子空间拟合（WSF）的 DOA估计中非线性多维搜索的问题。计算机仿真结果表明：基于模拟退火遗传算法的DOA估计方法在低信噪比条件下比基本遗传算法、高斯-牛顿算法有更高的分辨概率，更小的均方误差。

2 阵列模型

为了便于分析，本文以均匀线阵为例。假设有P个远场窄带信号入射到空间某阵列上，阵列天线由M个阵元组成，阵元间距为d。则阵列输出表示为

式（1）中，X(t)为阵列的M×1维快拍数据矢量，N(t)为阵列的M×1维噪声数据矢量，S(t)为P×1维的信号数据矢量，为M×P维阵列方向矩阵，其中第i个信号的导向矢量为[]T表示矩阵转置。

若假设P＜M，噪声为理想高斯白噪声，功率为2σ，且各阵元间噪声、噪声与信号之间相互独立，则阵列输出的协方差矩阵为

式（2）中，Rs为信号协方差矩阵，I为单位矩阵。

对R进行特征分解，考虑到信号源相干或非相干的情况，Rs的秩P′会小于等于信源个数P，则有

式（3）中，Us=[e1，e2，…，eP′]为信号子空间，UN=[eP′+1，eP′+2，…，eM]为噪声子空间，Σs=diag(λ1，λ2，…，λP′)为信号特征值组成的对角阵，噪声特征值组成的对角阵为ΣN=diag(λP′+1，λP′+2，…，λM)。

3 加权子空间拟合（WSF）算法

加权子空间拟合相当于子空间之间的拟合，既接收数据的子空间与实际信号导向矢量组成的子空间之间的拟合。文献[3]中给出了 WSF准则一般表达式

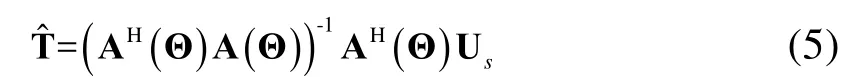
文献[3]中指出，当加权矩阵W满足下式时，Θ估计的方差最小。即

最后，将式（5）、（6）代入式（4）中化简可得WSF算法最终表达式为

4 模拟退火遗传算法

4.1 遗传算法

遗传算法（GA）模拟生物自然选择和遗传进化中发生的复制、交叉、变异等现象，以编码空间代替问题的可行解空间，以适应度函数作为个体评价依据，从任一初始种群开始，通过随机的选择、交叉和变异操作，产生更适应环境的子代群体，使得群体朝着最有希望的区域进化，通过这样的迭代过程不断繁衍进化，最后收敛到最适应环境的群体，继而可求出问题的最优解。图1是遗传算法的运算过程示意图。

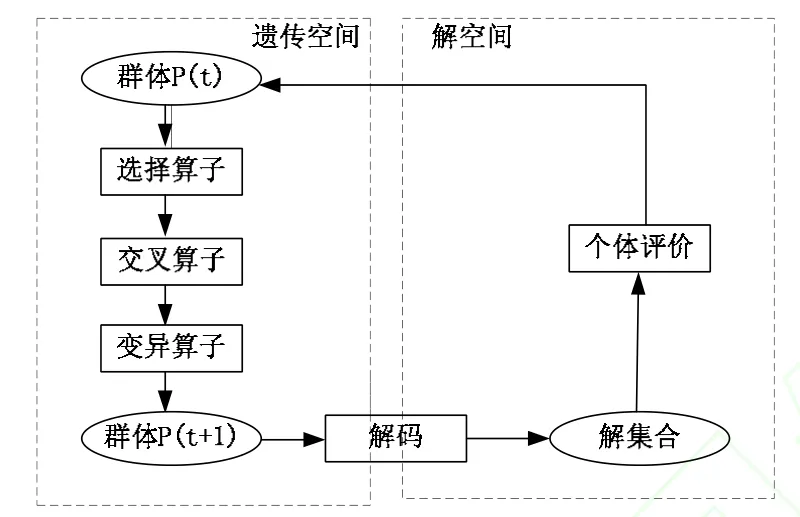
图1 遗传算法的运算过程示意

然而实践应用中，遗传算法在运算过程中很快收敛到局部最优解，并且运算后期在最优解附近左右摆动，收敛较慢[9]。

4.2 模拟退火算法

模拟退火算法（SA）是一种基于金属退火机理的随机寻优算法，通过随机搜索技术从概率意义上找出目标函数的全局最小点。在寻优过程中，当前解xold经随机扰动产生新解xnew，新解的接受概率由Meteopolis准则确定，即

式（8）中，Δ=f(xnew)-f(xold)为目标函数增量，Ti为当前温度值。

使用上述准则优势在于：当新解为更优解（即Δ＜0）时，以概率1完全接受新解为当前最优解；而当新解为恶化解（即Δ≤0）时，以概率接受恶化解为当前最优解，避免运算过程中陷入局部最优，并且随着温度参数Ti的减小，恶化解的接受概率也逐渐减小，最终收敛于全局最优解。

此外，实际应用中常采用指数降温方法来实现对温度的控制，即

式(9)中，Ti表示当前温度，T0为初始温度，k为温度下降系数。

图2给出了模拟退火算法的流程。但是模拟退火算法虽能摆脱局部最优，从而收敛到全局最优。但是这是以较高的初始温度、较慢的降温速率和较低的终止温度为代价的，再加上搜索过程中对整体的把握能力不够，所以该算法收敛到全局最优解是非常耗时的。在实际应用过程中，由于速度和时间的限制，很难保证优化结果为全局最优点。

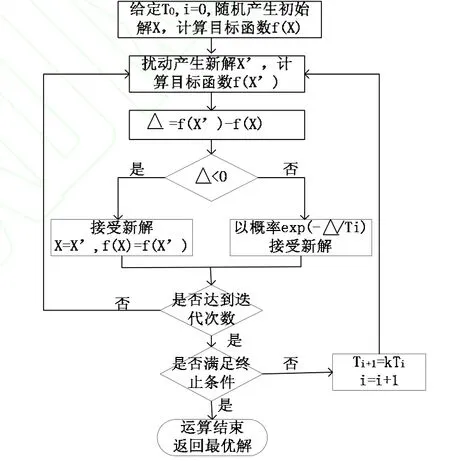
图2 模拟退火算法流程图

4.3 模拟退火遗传算法在DOA估计中的应用

遗传算法的局部搜索能力较弱，但搜索过程中整体把握能力较强；而模拟退火算法有较强的局部搜索能力，但对整个搜索空间的状况知之甚少，不利于搜索过程朝着最有希望的区域进行。若将两者相结合，互相取长补短，可得到一种性能优良的新的全局搜索算法。因此利用模拟退火遗传算法可以有效搜索出满足式（7）的到达角，即选取作为算法的适应度。考虑到模拟退火算法一般用来求解最小值，而此处需要求解最大值，所以Metropolis准则的表达式需要做出相应的改变，即令

本文首先对遗传算法的初始种群进行改进，并使用格雷编码，然后将模拟退火思想融入到遗传算法中，设计出模拟自适应交叉概率、变异概率，并且按照Metropolis准则来判断是否接收交叉、变异等操作后产生的新解。算法主要流程如下：

（1）参数的初始化。设定遗传种群规模N，初始化温度T0，阵元数M，信源数P等。

（2）编码。采用格雷编码方法。

（3）初始种群的产生。初始种群的特性对计算结果和计算效率有着重要影响。在无法预知最优解所在区域的情况下，要实现全局最优解，初始种群在解空间中应尽量分散。文献[11]中指出，若要取一定的点数，用佳点集法比用随机法的偏差小得多，从而更有利于算法的快速收敛。本文采用佳点集均匀设计的方法来设计初始种群，即在解空间内（即P维欧氏空间内），利用佳点集均匀设计的方法产生N个染色体作为初始种群，具体产生方法如下[11]：

（5）选择。采用比例选择方法，从当代群体中选择优良个体遗传到下一代。

（6）自适应交叉概率和变异概率

交叉概率 Pc和变异概率Pm的选择直接影响着算法的收敛特性，交叉运算是产生个体的主要方法，而变异运算只是产生新个体的辅助方法，二者分别决定了算法的全局和局部的搜索能力。遗传算法计算过程中，可将进化过程分为渐进和突变两个阶段：渐进阶段强交叉，弱变异，强化选择算子；突变阶段弱交叉，强变异，弱化选择算子，这样有利于提高计算速度和效率[9]。文中的 Pc和Pm依据模拟退火的思想按照以下公式进行自适应的调整：

式（12）、（13）中，T′为遗传算法当前进化代数的倒数，Rini为遗传迭代次数。在进化初期T′较高，Pc较大，Pm较小，算法侧重全局搜索，快速收敛到最优解附近区域；随着进化代数的增加，T′逐渐减小，Pc渐进减少，而Pm渐进增加，算法侧重局部搜索，避免算法收敛到局部最优解，从而提高算法的计算速度和效率。

（7）交叉和变异。随机选取两个个体Bi和Bj进行交叉、变异，产生新个体Bi′、，计算 f(Bi)和和，然后融入模拟退火思想，并按照式（10）的Metropolis准则来判断是否接受新个体。

（8）最优保存策略。计算经交叉、变异后个体的适应度值，与前一代中个体适应度值进行比较，将适应度值最高的个体保留到下一代群体中。

（9）终止条件的判断。若已经达到设定的最大遗传代数，则迭代过程终止，输出最优解；若不满足终止条件，温度更新 Ti+1=kTi，并转至第（4）步并继续进行迭代寻优过程。

5 计算量分析

根据文献[8]计算复杂度的方法，若定义M维矩阵相乘的计算量为Δ，则可以推出 WSF算法、基于遗传算法求解WSF问题的计算复杂度分别为

式（14）、（15）中，range为角度搜索范围，q为步长，Rini为遗传迭代次数。

由式（14）可知，WSF算法的运算量随着信源个数的增加以几何级数增长。当信源数P较大时，有

由于遗传算法的运算量主要由初始种群个数和迭代次数决定的，所以在相同N和Rini情况下，文中的模拟退火遗传算法的计算复杂度与基本遗传算法的计算复杂度差距并不算大。

6 仿真分析

仿真环境：均匀线阵阵元数为 16，阵元间距为半波长，假设有2个远场窄带不相干信号源，入射角度分别为-2°和2°，快拍数为 1000，噪声为零均值、单位方差的高斯白噪声，且信号与噪声之间相互独立。遗传算法中参数设置分别为：N=40，Rini=150，Pc=0.6，Pm=0.001。模拟退火遗传算法中参数设置分别为：T0=100000，ρ=0.9。高斯—牛顿法中参数设置分别为：最大循环次数 100，误差容限0.001，µ=1，采用二分法确定每次迭代中的µ值，即µ=µ2。

仿真 1：随机方法和佳点集方法产生的初始种群分布对比。为了便于比较，将初始种群规模设为300。仿真结果分别如图3、图4所示。

图3 随机产生的初始种群分布

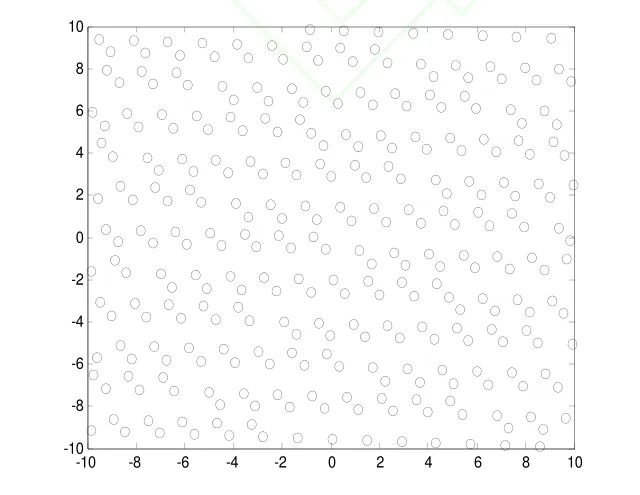
图4 佳点集产生的初始种群分布

对比图3、图4可以看出，佳点集法比随机法产生初始种群分布要均匀、没有重叠点、种群有较好的多样性，有利于算法的快速收敛和全局优化。

仿真2：遗传算法、模拟退火遗传算法和高斯-牛顿算法性能比较。信噪比为-10dB～10dB，独立进行100次Monte-Carlo实验，各算法对2个信号源方位的均方误差、分辨成功概率如图5、图6、图7所示。

图5 信号源1估计均方误差

图6 信号源2估计均方误差

图7 3种算法的分辨成功概率

由图5、图6可以看出，模拟退火遗传算法的估计均方误差最小，并随着信噪比的增大，均方误差趋近于 0。若定义算法的分辨门限为分辨成功概率超过90%时所对应的信噪比值，通过图7可以看出，模拟退火遗传算法的分辨门限为-8dB，高斯-牛顿算法的分辨门限为-3dB左右，而基本遗传算法的成功分辨概率始终低于90%。

7 结论

子空间拟合算法虽有较好的估计性能，但由于算法涉及到非线性多维搜索，角度搜索非常耗时，限制了该类算法在实际中的应用。而本文提出的基于模拟退火遗传算法的子空间拟合实现算法具有很强的抗早熟能力，并且在收敛速度和估计精度方面性能比较理想。除此之外，模拟退火遗传算法还可用在MUSIC等其他DOA估计算法和目标波束空间DOA估计中，因此具有广阔的应用前景。

[1]Schmidt R O.Multiple emitter location and signal parameter estimation [J].IEEE Trans.on AP,1986,34(3):276-280

[2]Roy R, Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques [J].IEEE Trans.on ASSP,1989,37(7):984-995

[3]Viberg M, Ottersten B, Kailath T.Detection and estimation in sensor arrays using weighted subspace fitting [J].IEEE Trans.on SP,1991,39(11):2436-2449

[4]Krim H, Viberg M.Two decades of array signal processing research [J].IEEE Trans.on SP,1996,13(4) :67-94

[5]Agoston E E, Rober T H, Zbigniew H M.Parameter control in evolutionary algorithms [J].IEEE Trans.Evolutionary Computation,1999,3(2):124-141

[6]Karamalis P, Marousis A, Kanatas A.Direction of arrival estimation using genetic algorithms[C].Vehicular Technology Conference, Rhodes, 2001:162-166

[7]Li M, Lu Y.Genetic algorithm based maximum likelihood doa estimation [C].International Rader Conference(RADER2002), 2002:502-506

[8]金勇，程云志，周柯.基于遗传算法的宽带目标波束空间DOA估计[J].传感器与微系统，2008，27(7):53-56

[9]雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社，2005

[10]王凌.智能优化算法及其应用[M].北京：清华大学出版社，2001:17-35

[11]张玲，张钹.佳点集遗传算法[J].计算机学报，2001，24(9):917-922