模糊神经网络变幅液压系统故障诊断

冯文洁，李万莉，嘉红霞

FENG Wenjie1,LI Wanli2,JIA Hongxia3

1.同济大学 机械与能源工程学院，上海 201804

2.上海海事大学 物流工程学院，上海 201306

1.School of Mechanical Engineering,Tongji University,Shanghai 201804,China

2.School of Logistics Engineering,Shanghai Maritime University,Shanghai 201306,China

1 引言

变幅液压系统结构复杂，由大量的动力元件、控制元件和执行元件有机组合而成，各组成元件在一个工作循环中通过不同的动作完成特定的任务，因此系统内部各元件之间耦合性强，系统故障及其故障原因具有多样性、模糊性及偶然性的特点。

模糊神经网络利用神经网络的自学习功能，优化模糊逻辑系统中的模糊规则、隶属函数和模糊决策算法；将神经网络的学习结果转化为模糊逻辑系统的规则知识，从而更有利于知识的解释与利用，非常适用于复杂对象的过程监测与故障诊断[1-3]，则对变幅液压系统故障诊断具有非常大的优越性。学习样本的归纳一直是神经网络应用的一大难点[4]。故障树描述并存贮了系统关于故障树顶部事件发生的全部知识，通过构建变幅液压系统故障树，由故障树提取变幅液压系统模糊神经网络的训练数据，既克服了提取训练数据的盲目性，又可包含系统的全部故障模式，使神经网络学习数据的归纳简单易行。

因此，本文以基于故障树的模糊神经网络故障诊断方法对变幅液压系统进行故障诊断。

2 变幅液压系统工作原理

图1为变幅液压系统工作原理图。变幅换向阀4右位时，变量泵1高压油，经平衡阀5的单向阀，进入变幅缸6大腔，小腔回油，缸活塞杆伸长，驱动工作臂逆时针转动，减小幅度，提高起升高度。换向阀4左位时，高压油进入小腔，在重力作用下下降，由于平衡阀产生背压作用，臂平稳下降，减少起升高度，加大幅度。换向阀处于中位时，由于平衡阀5具有锁的作用，使臂在作业时，不会产生沉降，保证机械的稳定性。

图1 变幅液压系统工作原理图

分析可知变幅液压系统结构复杂，由动力元件、控制元件和执行元件有机组合而成，各组成元件在一个工作循环中通过不同的动作完成特定的任务，因此系统内部各元件之间耦合性强，系统故障及其故障原因具有多样性、模糊性及偶然性的特点。基于以上故障特点分析，本文提出以模糊神经网络作为变幅液压系统的故障诊断方法。

3 变幅液压系统模糊神经网络故障诊断模型

根据故障树知识以及模糊神经网络的特点，首先，从故障树知识中提取模糊神经网络输入参数；其次，收集一定量的样本数据，运用统计参数法中的3σ准则法确立模糊化处理的模糊隶属函数，并对模糊神经网络输入参数进行模糊化处理；再次，建立神经网络推理计算的权值和阈值的训练算法；最后，对模糊化的输入参数进行训练并清晰化训练结果。由此构建变幅液压系统模糊神经网络故障诊断模型[5-6]，如图2所示。

3.1 变幅液压系统故障诊断输入输出节点的确定

在变幅液压系统故障诊断模糊神经网络中，网络的输入变量表达系统的故障征兆或故障模式的特征参数，输出变量则表达系统的故障原因或故障模式。为了确定变幅液压系统故障诊断网络的输入及输出变量，以变幅无动作为例，建立变幅无动作的故障树，如图3所示。

图2 变幅液压系统故障诊断模糊神经网络

图3 变幅无动作故障树

故障树中各基本事件的表述如表1所示。

表1 变幅无动作故障树基本事件

根据故障树最小割集的定义及上行法计算可知，变幅液压系统故障树中每一个基本事件就是一个最小割集，只要检测主泵压力、变幅大腔压力、变幅小腔压力及平衡阀控制油口压力即可分辨无故障、{X1-X2}、{X3}、{X4-X5}、{X6-X7}及{X8-X10}这六种故障模式，因此这4个特征参数即为故障诊断网络输入变量，输出变量为6个。

3.2 变幅液压系统故障诊断输入变量的模糊化处理

3.2.1 变幅液压系统故障诊断输入变量模糊化隶属度函数

通过隶属度函数[7]将输入变量转换成对应模糊子集上的隶属度。模糊层的作用即利用隶属度函数将输入变量进行模糊量化预处理，使之符合模糊神经网络的输入要求，模糊化采用的隶属度函数，如图4所示[8-9]。

图4 模糊隶属度函数

图4中，状态变量域低的转换采用降半梯形分布的隶属函数，其表达式如（1）所示。

状态变量域正常的转换采用梯形分布的隶属函数，其表达式如（2）所示。

状态变量域高的转换采用升半梯形分布的隶属函数，其表达式如（3）所示。

特征参数的模糊化处理是将输入的精确特征参数值转换成模糊隶属度值。根据上述分析，首先将输入的特征参数变换到各自所属的论域范围即低、正常和高，然后将已经变换到论域范围的特征信号参数根据各个论域的隶属度函数进行模糊化处理，使原来精确的输入量变成0～1之间的模糊隶属度值。

3.2.2 变幅液压系统故障诊断隶属度函数参数的计算

在收集一定量的设备正常工作时的样本数据基础上，运用统计参数法中的3σ准则法[10-12]确定隶属函数各参数的值。设备正常工作时的各类诊断参数即模糊神经网络输入变量xi服从正态分布规律，对正常工作时各类诊断参数xi收集一定量的训练样本数据，样本个数设为N，然后求取各输入变量的样本均值，其中xik为模糊神经网络第i个输入变量的第k个样本：

设σ为标准方差，则：

若诊断参数xi服从正态分布，那么，在±3σ范围内包含了99.73%的质量特性值。按正态分布理论根据3σ原理，如果测试样本与均值距离在3倍方差以上，则认为该测试样本是不确定的，故可判为异常，以此可以确定控制界限[11-12]：故障界限：X±3σ；警告界限：X±σ或者 X±2σ 。

将3σ原理应用于隶属函数各参数的确定，a为故障下限，d为故障上限，b为警告下限，c为警告上限，可得到模糊神经网络中第i个输入变量的隶属函数参数计算公式为：

3.3 变幅液压系统故障诊断神经网络推理

3.3.1 变幅液压系统故障诊断神经网络权值和阈值的求解

第一层故障树层可知输入变量的个数，设输入变量为n，则节点数为n，其输入输出为：i=1，2，…，n。故障树层直接将输入变量传递给第二层模糊化层，在基于故障树的模糊神经网络中，输入变量为系统的故障征兆。因此第二层的输出节点数仍然为n，其输入输出为：

第三层为神经网络推理层，神经网络推理层神经元采用的传递函数是tansig。

设该隐含层节点为q个，节点的输入输出为：

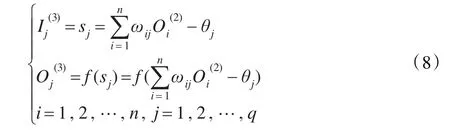
式中ωij为第二层第i个节点到第三层第 j个节点的连接权值，θj为第 j个节点的阈值，f(s)为tansig函数。

第四层为输出层，输出层神经元采用的传递函数是logsig。

式中ωjl为第三层第 j个节点到第四层第l个节点的连接权值，θl为第l个节点的阈值，f(s)为logsig函数。

3.3.2 变幅液压系统故障诊断神经网络权值和阈值的训练

运用Levenberg-Marquardt[13]优化算法对神经网络的连接权值和阈值进行训练，网络误差指标函数表达为[14-15]：

式中，Yq表示实际的神经网络输出向量，Yq'表示期望的神经网络输出向量，P为神经网络训练样本数目，w为神经网络权值和阈值组成的向量，eq(w)为误差。设wk表示第k次迭代的权值和阈值所组成的向量，wk+1=wk+Δw，运用Levenberg-Marquardt算法对网络的连接权值和阈值进行优化，权值与阈值组成向量的增量Δw计算公式为：

式中，J(w)为Jacobian矩阵，I为单位矩阵，μ为用户定义的学习率。

4 变幅液压系统故障诊断实验

通过搭建变幅液压系统故障诊断实验台以实现变幅液压系统故障诊断实验数据采集，为基于故障树的模糊神经网络各输入变量隶属函数参数值的计算及故障诊断提供实测数据，对基于故障树的模糊神经网络故障诊断方法的正确性和有效性进行验证。

变幅液压系统变幅无动作实验信号采集传感器包括4个压力传感器，由变幅无动作故障树可知采集的信号变量包括：PP-主泵压力；PA-变幅小腔压力；PB-变幅大腔压力；PC-平衡阀控制油口压力，压力传感器外形及安装如图5所示。

图5 压力传感器及安装

系统软件的实现采用LabVIEW软件的特色技巧——状态机模式。关于状态机的一个极度确切的描述是它是一个有向图形，由一组节点和一组相应的转移函数组成。将流程图各个过程转换为状态图，采用状态机结构实现了上述程序流程图。数据采集程序框图如图6所示。数据采集软件图形界面如图7所示。

图6 变幅液压系统故障诊断数据采集程序框图

图7 变幅液压系统故障诊断数据采集程序框图

5 变幅液压系统故障诊断实例分析

（1）变幅液压系统故障诊断模糊隶属度函数的参数计算

在实施中，在线采集检测信号进行故障诊断，利用式（4）至（6），可分别计算基于故障树的模糊神经网络四个输入变量对应的隶属度函数的参数值。

①主泵压力 PP，Yˉ=71.176 3 bar，σ=5.597 6，隶属度函数参数值为：{a，b，c，d}={54.383 5，65.578 7，76.773 9，87.969 2}。

②变幅小腔压力PA，Yˉ=3.907 2 bar，σ=0.009 5，隶属度函数参数值为：{a，b，c，d}={3.878 7，3.897 7，3.916 7，3.935 7}。

③变幅大腔压力PB，Yˉ=53.712 8 bar，σ=0.025 6，隶属度函数参数值为：{a，b，c，d}={53.63，593.687 1，53.738 4，53.789 7}。

④平衡阀控制油口压力PC，Yˉ=21.095 5 bar，σ=0.062 3，隶属度函数参数值为：{a，b，c，d}={20.908 7，21.033 2，21.157 7，21.282 3}。

（2）变幅液压系统故障诊断神经网络权值和阈值的优化训练

对每个输入变量取模糊子集0.1、0.5、0.9分别表示压力过低、正常、过高。由此提取神经网络权值及阈值的训练样本，如表2所示。

表2 变幅无动作神经网络训练样本

运用Levenberg-Marquardt算法对神经网络进行训练，神经网络输入节点为4个，输出节点为6个，根据Kolmogorov定理可确定隐含层的节点数为8个，训练结果如图8所示，从图可以看出，神经网络经过5次训练即已达到期望目标。

图8 目标函数训练曲线

Levenberg-Marquardt法实际上是梯度下降法和牛顿法的结合，它的优点在于网络权值数目较少时收敛非常迅速。应用Levenberg-Marquardt优化算法比传统的BP及其他改进算法迭代次数少，收敛速度快，精确度高。因此Levenberg-Marquardt优化算法与其他训练算法相比在BP网络学习中具有一定优越性，神经网络训练算法比较如表3所示。

表3 神经网络训练算法比较

为了验证故障诊断方法的有效性，将变幅无动作下采集的故障数据{PP，PA，PB，PC}={70.536 8 bar，4.015 6 bar，53.674 2 bar，4.018 9 bar}作为模糊神经网络的输入，将输入数据进行模糊化处理，求得各输入变量对应论域的隶属度为 {0.124 7，0.374 8，0.783 0，0.421 5}，经过网络计算得到输出为：{0.001 8，0.001 3，0.001 4，0.002 5，0.998 7，0.001 6}，由表2中故障模式描述可知，该输出与故障模式中的F5对应程度非常高，即X6控制器或手柄损坏或X7先导比例减压阀损坏，实际状况是操作手柄与变幅换向阀断接导致控制腔压力未建立，诊断结果与实际状况一致。

6 结束语

变幅液压系统是各机构控制回路中最复杂的系统之一，传统的故障推理算法难以满足这类复杂系统故障诊断的要求。本文提出了一种基于故障树的模糊神经网络故障推理机制，该机制融合了故障树和模糊神经网络两种方法的优点，研究了变幅液压系统模糊神经网络故障诊断推理机制的研制过程，以顶事件变幅无动作为对象，通过实例验证了该故障诊断方法的可行性和有效性。

[1]吴宗彦，韩煜，张建军，等.基于模糊神经网络的自动生产线故障诊断方法研究[J].中国机械工程，2008（9）：1072-1075.

[2]Yznaga Blanco I，Sun D，He Y K.Neural-fuzzy technique for inverter faults diagnosis in PMSM DTC system[J].Electric Machines and Control，2008，12（3）：132-139.

[3]张敬芬，孟光，赵德有.基于模糊神经网络的薄板不同指标裂纹诊断[J].机械工程学报，2006（3）：145-149.

[4]陈炜，吴志良.故障诊断专家系统结合故障树技术的结构研究[J].航海技术，2005（6）：47-49.

[5]艾芳菊.模糊神经网络的结构优化研究[D].成都：中国科学院研究生院成都计算机应用研究所，2006.

[6]姜长元.模糊神经网络模型及其应用研究[D].南京：南京师范大学，2005.

[7]彭广平，李泳鲜.模糊神经网络在汽车发动机电子点火系统故障诊断中的应用[J].汽车科技，2011（3）：47-50.

[8]孙增国.神经网络和模糊专家系统在故障诊断中的应用[D].辽宁大连：大连理工大学，2004.

[9]张婷.模糊神经网络在冷水机组故障诊断中的应用研究[D].天津：天津大学，2009.

[10]Pltkeisheim F.The three sigma rule[J].The American Statistician，1994，48（2）：88-91.

[11]赵伟.船舶柴油机监测与故障诊断技术研究[D].辽宁大连：大连海事大学，2006.

[12]李琼.信息融合技术在航空发动机智能监测中的应用研究[D].南京：南京航空航天大学，2011.

[13]杨柳，陈艳萍.一种新的Levenberg-Marquardt算法的收敛性[J].计算数学，2005（1）：55-62.

[14]毛明明，柳益君，汤嘉立.基于L-M神经网络的齿轮故障诊断[J].计算机技术与发展，2011（1）：210-213.

[15]柳益君，古春生，朱广萍，等.LM神经网络在环境质量评估中的应用[J].江南大学学报：自然科学版，2010（2）：213-216.