永磁同步电机MTPA预测控制方法研究

闭业宾，罗显光，阮灵通，王达鹏，陈 优，李 洲

BI Yebin,LUO Xianguang,RUAN Lingtong,WANG Dapeng,CHEN You,LI Zhou

湘潭大学 机械工程学院，湖南 湘潭 411105

School of Mechanical Engineering,Xiangtan University,Xiangtan,Hunan 411105,China

1 引言

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）[1-4]以快速动态性、宽调速范围、结构简单等优点得到广泛的关注。为了充分利用永磁同步电机（PMSM）的磁阻转矩，人们期望以最小的定子电流来获取最大的电磁转矩输出，即实现最大转矩每安培（Maximum Torque Per Ampere，MTPA）[5-6]。鉴于MTPA控制的诸多优势，国内外学者对其进行了很多的研究，主要集中于：公式计算法[7]、查表法[8]以及梯度下降法[9]等。纵观上述三种方法，其实现MTPA优化控制的过程是一个线性单目标的优化，全过程中难以兼顾到转矩跟踪、电流限幅等辅助优化指标。

模型预测控制（Model Predictive Control，MPC）作为一门20世纪70年代发展起来的非线性控制理论[10-14]，由于其在处理复杂约束问题时所展现出的突出优势，逐渐被应用于多个工程领域之中。近年来，伴随着数字处理技术的飞速发展，越来越多的以电力电子领域为代表的快速系统开始应用预测控制方法来提高其约束处理和控制性能[15-16]。本文从优化永磁同步电机（PMSM）磁阻转矩角度出发，提出了一种PMSM最大转矩电流比（MTPA）预测控制优化方法。该方法在建立PMSM调速系统电磁转矩离散预测模型的基础上，重点研究了其MTPA优化的内在机理与典型问题。进而构建了一个以电磁转矩跟踪、MTPA优化以及系统限流保护为目标的预测控制价值函数，该价值函数可以在线自适应地识别出PMSM调速系统的动、稳态情况，并根据相应的识别结果重点突出各个优化目标项，从而实现PMSM调速系统的全局最优控制。实验结果表明，该方法有效地提升了PMSM调速系统的运行效率，同时其保留了预测控制多目标优化、高动态响应等控制优势。此外，在实现MTPA优化控制时该方法对电机参数的变化展现出较强的鲁棒性。

2 系统数学模型

图1为三相电压型PMSM调速系统结构图，其中Udc为直流母线电压；S1～S6为6个功率开关器件；uabc为逆变器三相输出端口电压。

图1 三相电压型PMSM调速系统结构图

假设系统为三相理想对称系统，引入abc/dq旋转坐标变换后，可以建立系统在两相旋转dq坐标系下的数学模型如下：

电气方程：

式中，udq、idq为 dq轴定子电压和电流；Rs、Ldq为定子电阻和dq轴电感；Ψm为转子磁链；Te为电机电磁转矩；ωe为电机电角度；np为电机极对数。

假设数字处理系统以一个足够高控制频率进行系统控制，可以认为其各个变量在一个控制周期内以恒定的增、减趋势变化，此时可将式（1）中的微分项等效为：

式中，上标k、k+1表示对应时刻的数字系统采样值。

将式（3）代入式（1）后，即可求得系统的离散预测模型为：

进而可得第k+1时刻的电磁转矩预测值为：

3 MTPA优化原理

为了进一步优化PMSM调速系统的运行效率，希望以最小的定子电流来获取最大的电磁转矩输出，即实现最大电流安培比（MTPA）的控制效果。考虑到永磁同步电机存在的凸极效应特性，此时需要充分地利用PMSM的磁阻转矩，为此一个辅助优化项被加入系统优化中，具体过程如下：

建立dq旋转坐标系下的PMSM调速系统空间矢量分析图，其中定子电流矢量idq与q轴呈β角度关系，此时dq坐标系下的电流分量为：

式中，im为定子电流幅值。

将式（6）代入转矩方程式（2）可得：

图2 PMSM空间矢量分析图

当式（7）中定子电流幅值im为固定值时，为了得到最大的电磁转矩输出，需要求取一个最优的夹角β，即求取以夹角β为变量的式（7）的极值点，此时进行微分计算如下：

从图2可以看出，id、iq、β三者之间满足以下关系：

联立式（8）、（9）可知，当 id、iq满足式（10）的关系时，PMSM调速系统运行于MTPA的最优轨迹之上。

4 多目标优化

预测控制（MPC）作为非线性控制的典型代表，与传统线性PID控制相比，MPC可以实现对多个目标的综合优化。以本文研究的PMSM调速系统MTPA优化为例，其优化目标包含：电磁转矩控制、MTPA优化以及系统限流保护三大部分，下文给出了上述三个优化目标的具体实现方法。

（1）电磁转矩控制

电磁转矩控制作为PMSM调速系统的核心优化目标，为了获得一个高精度、高动态特性的电磁转矩控制效果，构建转矩控制目标函数如下：

（2）MTPA优化

将式（9）代回式（8）即可求得MTPA情况下的 id、iq关系如下：

至此构建MTPA目标函数如下：

（3）限流保护

为了保证功率器件和电机系统的安全，需要对其允许通过的最大电流加以限制，令上述最大电流为imax。此时，可以在价值函数中引入一个限流保护项如下：

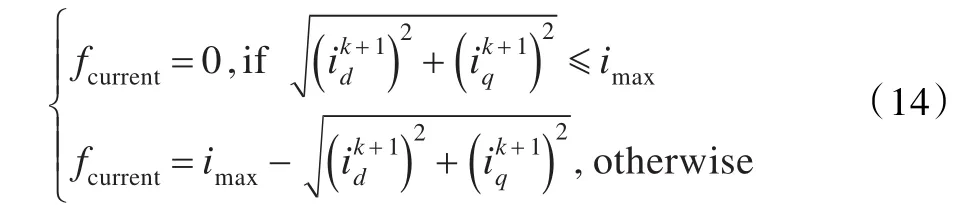
当PMSM调速系统的电流幅值小于imax时，表明系统并无过流问题，此时系统限流保护为0，其不参与在线优化；当PMSM调速系统的电流幅值大于imax时，表明系统出现过流危害，此时系统限流保护将参与到在线优化中，可以有效地避免过流问题造成功率器件、电机绝缘的损坏。

（4）价值函数

综上可知PMSM调速系统MTPA预测控制方法的在线优化价值函数[16]如下：

式中，KTe、KMTPA、Kcurrent为价值函数权值系数，通过配置不同的权值系数可以得到不同的多目标优化效果；i∈[0，7]表示VSI系统的8个开关状态对应序号。

可以看出，价值函数由电磁转矩控制、MTPA优化以及限流保护三部分组成，其中：电磁转矩控制项将在系统动态过程中占据主导地位，此时系统存在较大的转矩跟踪误差，该项可以实现电磁转矩的快速跟踪响应，从而消除系统转速跟踪误差；MTPA优化项将在系统稳态过程中占据主导地位，此时系统根据实际负载转矩值进行转矩电流和励磁电流的合理分配，从而使得PMSM调速系统始终运行于MTPA最优轨迹上；限流保护项用于保障系统的安全性，当PMSM的定子电流幅值超出其最大值时，限流保护项将投入运行，从而避免因过流问题而造成的PMSM调速系统损坏。

5 仿真与分析

为了验证所提永磁同步电机MTPA预测控制方法的可行性，基于Matlab/Simulink软件进行了系统仿真实验。仿真系统的主要参数如下：系统控制周期为0.000 1 s、电机额定电压380 V、电机额定电流38 A、定子电阻0.186 Ω、d轴电感12 mH、q轴电感35 mH、转子磁链1.1 Wb、电机极对数4、逆变器直流母线电压600 V。图3为永磁同步电机MTPA预测控制方法原理框图，由图可知系统采取了转速PI外环、转矩MPC内环的双闭环结构。

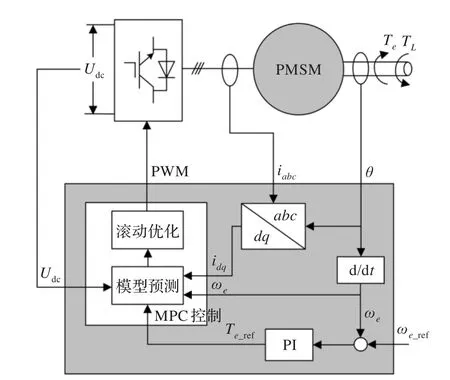
图3 MTPA预测控制方法原理框图

图4 PMSM调速系统全局运行效果图

如图4所示为PMSM调速系统全局运行效果图，其中电机转速给定值为额定转速1 500 rad/min，整个过程由四部分组成。当t=[0～0.05 s]时，电机由零速快速加速至额定转速（1 500 r/min），期间定子电流幅值达到电机限幅imax=40 A，随后电机进入空载稳态运行阶段，定子电流维持在零附近波动；当t=[0.05～0.1 s]时，电机被施加了一个正向的额定负载，调速系统快速地响应该负载变化，仅需约3 ms的时间即可完成电磁转矩响应。随后电机进入满载稳态运行阶段，为了优化PMSM调速系统的运行效率，MTPA优化项将励磁电流id控制为-15 A；在t=[0.1～0.2 s]阶段，PMSM逐步进入反向加载阶段，随着负载转矩的变化励磁电流id可以有效地进行自适应调节，整个过程中PMSM始终运行于MTPA最优轨迹上。

如图5所示为PMSM定子电流运行轨迹，在经历了空载加速、正向加载、反向加载等多个运行过程后，可以看出PMSM定子电流始终运行于MTPA最优轨迹上，整个过程中定子电流始终运行于最大电流圆环之内，说明调速系统并未出现过流危害现象。此外，当定子电流轨迹在空载点和满载点之间切换时，其中间过程的电流轨迹极为稀疏，表明系统可以由一个稳态快速地切换至另一个稳态，说明系统具备极强的动态响应性能。当电流轨迹稳定于某一稳态时，其在一个范围不大的圆环内轻微抖动，说明系统具备较为优异的稳态跟踪性能。综上可知，采取MTPA预测控制的PMSM调速系统具备优异的稳态、动态性能。

图5 PMSM定子电流运行轨迹

如图6所示为PMSM调速系统MTPA预测控制方法鲁棒分析结果，其中PMSM调速系统运行于稳态额定负载工况。分析参数准确时的定子电流波形可知，iabc保持较高的正弦度且电流脉动较小，对应的畸变率分析值仅为3.55%，此时的PMSM调速系统处于一个较好的运行状态；为了验证系统的鲁棒性，将PMSM的主要参数 Ld、Lq、Rs、Ψm设置为实际值的1.5倍，即 Ld=18 mH、Lq=52.5 mH、Rs=0.279 Ω、Ψm=1.65 Wb。可以看出此时电流脉动发生轻度恶化，但仍保持着较高的正弦度，对应的畸变率分析值上升至5.64%，仍属于电机安全运行允许范围之内。至此可知，PMSM调速系统MTPA预测控制方法具有较强的鲁棒性能，即使在电机参数发生大幅度失配的情况下，也能保持较好的系统控制效果。

6 结束语

本文在建立PMSM调速系统电磁转矩离散预测模型的基础上，研究了一种永磁同步电机MTPA预测控制方法，可以得出以下结论：

（1）MTPA预测控制方法可以实现电磁转矩跟踪、MTPA优化以及系统限流保护等多项目标的综合优化。

图6 PMSM调速系统电流轨迹图

（2）MTPA预测控制方法在优化PMSM调速系统运行效率的同时，保留了预测控制高动态响应的优点。

（3）MTPA预测控制方法具有较强的参数鲁棒性，在电机参数发生较大变化时，仍能保持较优异的系统控制效果。

[1]刘恒.永磁同步电动机混沌系统光滑二阶滑模控制[J].计算机工程与应用，2012，48（21）：222-224.

[2]董苏，赵烨，戴鹏.一种新型IPMSM无位置传感器矢量控制系统研究[J].电气传动，2013，43（5）：11-15.

[3]王新，胡路东，徐娟.PMSM矢量控制在高端波轮洗衣机中应用的研究[J].电气传动，2012，42（12）：10-13.

[4]朱磊，温旭，辉赵峰.永磁同步电机弱磁失控机制及其应对策略研究[J].中国电机工程学报，2010，18（31）：67-68.

[5]万健如.基于MTPA的永磁同步电机滑模变结构直接转矩控制[J].电机与控制学报，2012，16（3）：30-35.

[6]廖勇，伍泽东，刘刃.车用永磁同步电机的改进MTPA控制策略研究[J].电机与控制学报，2012，16（1）：12-17.

[7]李长红，陈明俊，吴小役.PMSM调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报，2005，25（21）：169-174.

[8]徐涛，陈义衡.基于电压极限椭圆梯度下降法的永磁同步电动机弱磁控制的研究[J].煤矿机电，2012（4）：18-23.

[9]席裕庚，李德伟.模型预测控制——现状与挑战[J].自动化学报，2012，38（9）：1-15.

[10]席裕庚，李德伟.预测控制定性综合理论的基本思路和研究现状[J].自动化学报，2008，34（10）：1225-1234.

[11]李志军.饱和约束系统的鲁棒模型预测控制[J].控制与决策，2006，21（6）：641-645.

[12]Rodriguez J，Pontt J，Cesar A.Predictive current control of avoltagesource inverter[J].IEEE Transactions on Industrial Electronics，2007，54（1）：495-503.

[13]曹晓冬，谭国俊，王从刚.一种低开关频率PWM整流器的满意预测控制策略[J].中国电机工程学报，2013，33（27）：69-77.

[14]Vargas R，Cortes P，Ammann U.Predictive control of a three-phase neutral point clamped inverter[J].IEEE Transactions on Industrial Electronics，2007，54（5）：2697-2705.

[15]杨兴武，姜建国.电压型PWM整流器预测直接功率控制[J].中国电机工程学报，2011，31（3）：34-39.

[16]杨勇，赵方平，阮毅，等.三相并网逆变器模型电流预测控制技术[J].电工技术学报，2011，26（6）：153-159.