基于改进粒子群算法的物流配送车辆调度

马冬青, 王蔚

MA Dongqing1, WANG Wei2

1.华北计算技术研究所, 北京 100083

2.太极计算机股份有限公司, 北京 100083

1.North China Institute of Computing Technology, Beijing 100083

2.TAIJI Computer Corporation Limited, Beijing 100083

1 引言

随着市场经济的蓬勃发展和物流水平的不断提高，物流配送对经济发展、商品流通和大众消费起到越来越重要的作用。采用科学的物流管理，是提高物流效率、降低成本、提高服务质量的重要途径。物流企业的管理涉及多个方面，其中配送是一个重要环节。配送指按照客户的要求进行收揽、派发。配送过程包括集货、分货、配货、配装、送货等多项活动，其中车辆配送是配送过程中的重要部分。配送车辆调度的优化目标是在满足客户需求及各种约束条件的同时，尽可能地节约成本。

由于配送受客户位置、客户要求、配送车辆能力等多种因素影响，导致车辆的调度问题十分复杂。如何利用有限的车辆资源尽可能高效地安排配送任务，降低成本，是物流车辆调度系统要解决的一项关键问题。概括来说，配送车辆调度问题是一个有约束的组合优化问题。

1959 年 Dantzig和 Ramser，提出物流配送车辆优化调度问题。物流配送车辆优化调度问题被归结为车辆路径问题（VRP）和多路旅行商问题（MTSP）。Dantzig是线性规划之父，在运筹学建树极高。物流配送车辆优化调度问题一经提出，就引起运筹学、组合数学、物流科学等多个领域专家的重视，开展了多方面的研究。多年以来，国内外对车辆路线问题之学术研究文献众多，也提出了相当多的求解策略与方法，包括：数学解析法、线性规划法、分支法、模拟退火法、节约法、蚁群算法、禁忌搜索法、遗传算法、人工神经网络法等。国外在该领域研究的代表人物有 Bodin、Golden、Laporte、Desrochers、Altinkermer等[1]。

国内对物流配送车辆优化调度问题也展开了许多研究。在建模方面，对问题模型进行细分，融入多种约束，解决各种不同限制及优化目标的车辆优化调度问题。在算法方面，对经典的TSP、VRP问题解决方法提出优化和改进方法，并提出基于混合策略的多种算法等。

本文参照经典车辆路径问题模型，建立了物流配送双向车辆调度问题的数学模型，并提出了基于改进粒子群算法的物流配送车辆调度算法。

2 双向车辆调度问题模型

物流配送车辆调度问题是安排有限的车辆按时间完成配送任务。每一车辆为具有一定需求的分布在不同地理位置的多个客户配送货物，在满足客户需求的约束条件下，找出配送成本最低的配送车辆调度方案。

例如，某配送中心有若干配送车辆，负责完成多个客户的配送任务，这些客户位于不同的地点，有的客户需要收货，有的客户需要发货。配送车辆设有单次配送里程上限和单次配送客户数上限，以便控制配送人员的劳动强度。配送车辆调度的任务是科学规划车辆行驶路线以及工作时间，生成优化的调度方案，在既定的约束条件下，使完成所有配送任务的总行驶里程最短。图1是配送车辆调度的示意图。

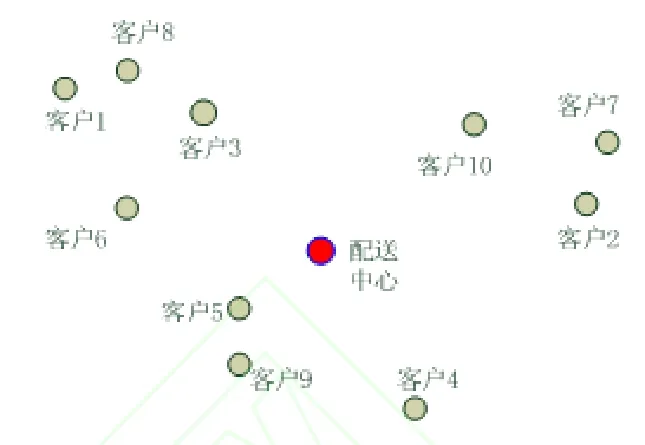
图1 配送车辆调度的示意图

2.1 范围

配送车辆调度受配送中心数量、配送车辆状况、配送任务特征、客户要求等多种因素影响，使得调度问题十分复杂。配送车辆调度问题可归类为一类有约束的组合优化问题。

本文从双向车辆调度问题入手展开研究。双向车辆调度问题具有如下约束：

(1) 一个配送中心、多个客户，配送中心和客户位置固定。

(2) 配送中心有多辆配送车，每车负责双向配送，即收揽和派发。

(3) 每辆车的载重量一定，不允许超载。

(4) 每辆车每次配送设有单次配送里程上限，不允许超出。

(5) 每辆车每次配送设有单次配送客户数上限，不允许超出。

(6) 车辆配送货物时从配送中心出发，最后返回出发地。

(7) 客户对配送时间无特殊要求。

可以看出，本文对现实中的物流配送调度问题进行了抽象和简化。选择双向车辆调度问题作为重点研究对象主要是出于以下几点考虑。

(1) 双向车辆调度问题是一类典型的配送调度优化问题。

(2) 物流管理系统中涉及的配送大部分可归类为双向车辆调度。

(3) 通过抽象简化问题，易于建模和求解。

2.2 模型描述

本文参照经典车辆路径问题模型，建立双向车辆调度问题的数学模型。

配送车辆调度问题是安排有限的车辆按时间完成配送任务。本文研究的配送车辆调度问题可以用如下的活动、资源、调度目标三要素来描述[2]。

活动指由配送中心为客户配送货物。配送中心数目是1，客户数目是M，客户位置固定，每个客户的货物重量为qi(i=1,2,…,M)。

资源指配送车辆。K辆配送车，各配送车的载重量为 Qk(k=1,2,…,K)，各配送车的单次配送里程上限为Dk(k=1,2,…,K)，各配送车的单次配送客户数上限为 Ck(k=1,2,…,K)。

调度目标是求解优化的调度序列。该调度系列在满足配送任务需要及车辆约束的情况下，实现配送里程最短。

依据上述目标建立的数学模型

其中，d0j(j=1,2,…,M)为配送中心到每个客户的距离，dij(i,j=1,2,…,M)为客户i到j的距离，nk为第k辆车配送服务的用户数(nk=0代表不使用第 k辆车)。Rk为第k条行驶路线，其中rk0=0代表配送中心，rki表示在路线k中第i个访问的客户。

在上述模型中，各式的含义是：

式（2-1）为目标函数，要求配送总里程最短。

式（2-2）为配送要求，要求每个客户的配送要求均需要满足。

式（2-3）为里程约束，调度安排各车辆配送时，要求各车辆配送任务不超过单次配送里程上限。

式（2-4）为载重量约束，调度安排各车辆配送时，要求各车辆不超载。

式（2-5）为是客户数约束，要求每条配送路线上的客户数不超过单次配送客户数上限，该限制的上限是客户数目M。

式（2-6）是表示每条配送路线的安排。

式（2-7）是隐含约束，要求每个客户仅由一台车配送。

3 基于混合粒子群算法的物流配送车辆调度算法

粒子群优化算法是由美国的 Kennedy和Eberhart于1995年提出的。粒子群优化算法是一种基于群体智能理论的优化算法，通过模拟鸟群的觅食过程，借鉴鸟群中的协作与竞争关系，不断演化来搜索最优解[3][4]。

本文参照标准粒子群优化算法构建了物流配送车辆调度算法的基本框架，并对标准粒子群优化算进行改进，在算法的多次迭代中引入爬山操作，增强了算法的局部搜索能力，实现了基于改进粒子群算法的物流配送车辆调度算法。

3.1 粒子群优化算法

在粒子群优化算法中，将每只小鸟抽象为一个粒子，用于表示问题的候选解。粒子的状态包括两个向量：位置向量和速度向量[5]。位置向量可以用式（3-1）表示，速度向量可以用式（3-2）表示。

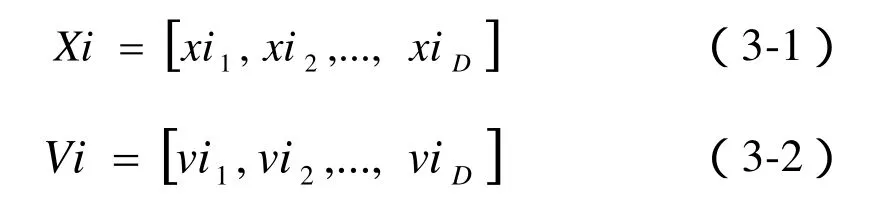
其中，D是解空间的维数，i表示粒子的编号。

粒子群中的粒子运动模拟了鸟群的活动，并融入了个体认知和社会影响。粒子群中粒子的位置受三方面的影响而改变。

(1) 粒子以当前的位置和速度为基础进行运动。

(2) 粒子运动受自身运动过程中的最好位置影响，即受个体认知的影响。粒子的优劣通过对粒子的位置进行适应度计算来确定。当前粒子的最好位置表示为pBest。

(3) 粒子运动受群体中所有粒子的最好位置影响，即受社会模式的影响。群体的最好位置表示为gBest。

粒子i在t+1时刻的状态表示为：

其中，ω是惯性权重，表示粒子当前位置对下一位置的影响程度；c1、c2是加速系数，分别表示粒子受个体认知和社会模式影响的程度；r1、r2是0到1之间的随机数。

粒子群优化算法的基本过程是首先随机构造初始粒子群，然后根据自身的最好位置和群体的最好位置来动态地调整自己的位置，通过多次迭代来搜索最优解[6]。

3.2 粒子编码

在本文的基于改进粒子群算法的物流配送车辆调度算法中，用实数编码的位置向量来表示配送车辆的调度序列。

在现有的研究成果中，在解决车辆路径问题时，解的表示方式多采用客户与虚拟配送中心共同排列的整数表示方法。由于整数表示方法不适用于进行粒子位置和速度的计算，本文借鉴处理器任务分配的实数表示方法来表示车辆配送调度序列。Ayed Salmen在解决处理器任务分配问题时，提出了实数向量的编码方式，用L维实数向量表示L个任务的配送车辆的调度序列[7]。

本文采用L维实数位置向量表示对L个客户的配送车辆的调度序列。向量中的每一维实数的范围是[0～M)，M表示车辆数。实数的整数部分，确定由哪一辆车为该客户服务，整数部分为0时表示，由第1辆车配送，整数部分为1时表示由第2辆车配送，以此类推。某辆车对客户的访问顺序，由实数小数部分从小到大的顺序决定。以8客户3辆配送车为例，粒子位置向量中的每一维均是0至3之间的实数。例如向量[2.418,2.873,2.615,0.158,0.002,2.211,1.896,2.716]中，第4、5维分别是 0.158、0.002，表示客户4、5由车1配送，按从小到大顺序，车1从配送中心出发，先为客户5配送，再为客户4配送，然后返回配送中心。如果用0表示配送中心，自然数表示客户，则上述粒子位置向量表示的调度序列为：

车1:0->5->4->0

车2:0->7->0

车3:0->6->1->3->8->2->0

粒子的位置通过解码过程转化为实际的配送车辆调度调度方案。

3.3 粒子评价

在本文基于改进粒子群算法的物流配送车辆调度算法中，粒子位置用于表示问题的解，即表示调度序列。调度序列的优劣通过对粒子的位置进行适应度计算来确定。为了评价解的优劣，首先通过解码得到该解所对应的调度序列，即配送路径方案，然后判断该配送路径方案是否满足问题的约束条件，同时计算该配送路径方案的目标函数值，在满足问题的各种约束条件的前提下，其目标函数值越优，则解的质量越高，配送方案越优。

在本文研究的物流配送车辆调度问题中，采用总里程作为调度序列的目标函数值，用于评判解的优劣。总里程小的调度序列优于总里程大的调度序列。总里程的计算公式为：

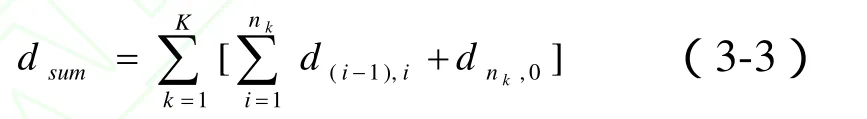
其中，dsum表示调度序列的总里程，K表示分配的车辆数，nk表示第 k 辆车配送的客户数，d(i-1),i表示从前一出发点（客户或配送中心）到客户i的行使里程。对于不可行的解，即调度序列不满足配送任务的需要或车辆的约束的情况，目标函数值取极坏值，并标志为不可用。

本算法中，目标函数值的计算过程是：

(1) 对备选解对应的调度序列进行解码。

(2) 检查备选解对应的调度序列中，是否满足所有客户的请求。如果有不满足的情况，则适应度设置为极坏值，并标志为不可用。

(3) 根据调度序列，分配各配送车任务。

(4) 计算各配送车的任务历程，检查是否超过车辆的运送能力。如果有超出的情况，则目标函数值设置为极坏值，并标志为不可用。

(5) 在调度序列满足配送任务的需要以及车辆的约束的情况，计算整个调度序列中各车任务的里程之和，作为解的目标函数值。

3.4 爬山操作

粒子群优化算法是一种简单易用、高效实用的智能优化算法，算法的优点是收敛速度快，但是容易落入局部最优。本文在标准粒子群算法的基础上，引入爬山操作，增加了粒子群的多样性，提高了算法的局部搜索能力。爬山算法是一种采用邻域搜索技术的、朝着有可能对解的质量产生改进的方向进行搜索的择优方法。这种方法具有较强的局部搜索能力。

本算法对粒子群优化算法各次迭代生成的新粒子逐个进行爬山操作，利用爬山算法局部搜索力强的特点，提高粒子群的适应度。本文根据实数编码的特点，采用单维突变的方式构造当前解的邻域。对于当前粒子，随机选取维数编号，对位置向量中选定维数的值进行随机设置，即对粒子的位置向量进行单维突变，得到新的位置向量。然后进行适应度计算，如果新的位置向量优于原位置向量，则接受新的位置向量，否则拒绝新的位置向量。通过增加爬山操作，可有效地增加粒子的多样性，增强局部搜索能力。

本文所采用的单维突变方法优于换位法、逆转法和插入法。爬山算法是基于邻域搜索的算法，在爬山算法中，通过邻域选点来构造新解。确定邻域选点方法是构成爬山算法的一个重要环节。解决组合优化问题通常采用的邻域选点方法包括换位法、逆转法和插入法。与换位法、逆转法和插入法相比，通过本文所采用的单维突变方法进行邻域选点，增加了车辆数目调整的可能性，扩大了邻域搜索范围。

3.5 算法流程

本文基于改进粒子群算法的物流配送车辆调度算法的基本流程是：

(1) 随机构造初始粒子群，生成各粒子的初始位置和速度。

(2) 评价粒子群的所有粒子，并记录各粒子的最好位置pBest和所有粒子的最好位置gBest。

(3) 按照式（3-3）和（3-4）更新各粒子的速度和位置。位置值越界时，设置为边界值。

(4) 对更新后的粒子进行爬山操作。采用的单维突变方法，进行邻域选点，得到新的位置向量。如果新的位置向量优于原位置向量，则接受新的位置向量，否则拒绝新的位置向量。

(5) 评价粒子群的所有粒子，更新每个粒子的最优位置和群体的最优位置。如果粒子位置的优于pBest，则更新pBest。如果粒子位置的优于gBest，则更新gBest。

(6) 若满足结束条件，则输出 gBest所为满意解。否则转到第3步继续迭代。

3.6 算法分析

粒子群算法可归类为群体智能算法，是一种随机搜索的全局优化算法。搜素过程从问题的一个解集合开始，在搜索过程中，通过群体中粒子间的相互协作与竞争进行迭代搜索，得到优化结果。粒子群算法计算简单，易于实现，控制参数少，实际应用中收敛速度较快。

粒子群算法属于随机算法，其收敛性目前没有严格的数学证明，而在广泛的实际应用中被证明是有效的。算法中惯性权重ω控制着前一速度对当前速度的影响，用于平衡算法的探索和开发能力，ω设为0.729的同时将c1和c2设为1.49445，有利于算法的收敛[8]。粒子群算法自身收敛速度较快，但是容易落入局部最优。本文基于改进粒子群算法的物流配送车辆调度算法，在标准粒子群算法的基础上引入爬山操作，增加了粒子群的多样性，提高了算法的局部搜索能力。

4 实验验证

为验证本算法的调度能力，本文采用两个固定的实验样本作为算法输入进行解算，利用计算机模拟产生一定区域内的配送中心位置及客户位置，并计算出配送中心与各客户之间以及各客户相互间的距离。实验样本1是3辆车8客户的调度问题，实验样本2是50辆车120客户的调度问题。实验中设每辆车单次配送里程上限为 80km，载重量为8t，单次配送客户数上限为30个客户。表1列出计算机模拟生成的实验样本 1的客户位置及货物重量。在表2中列出的是实验样本1的配送中心与各客户之间以及各客户相互间的距离。

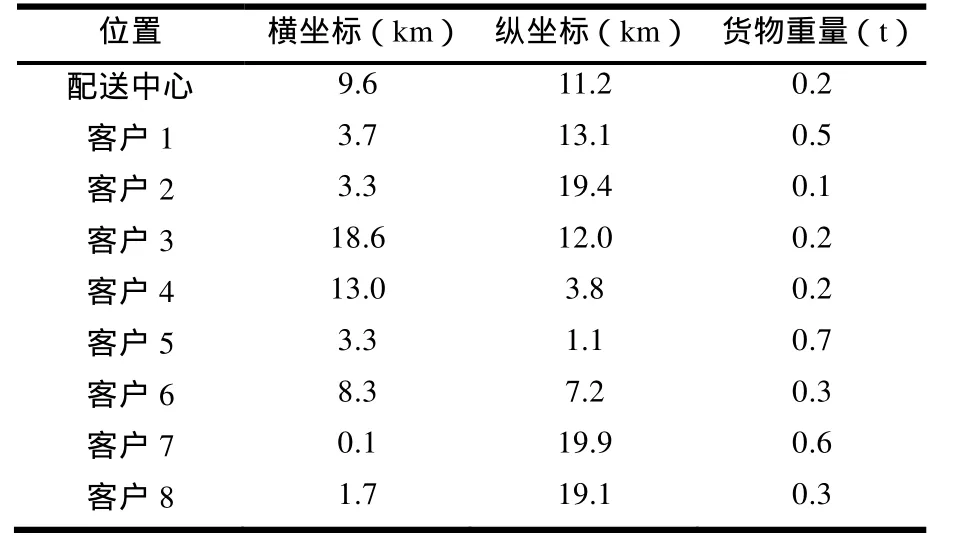
表1 实验样本1的模拟客户位置

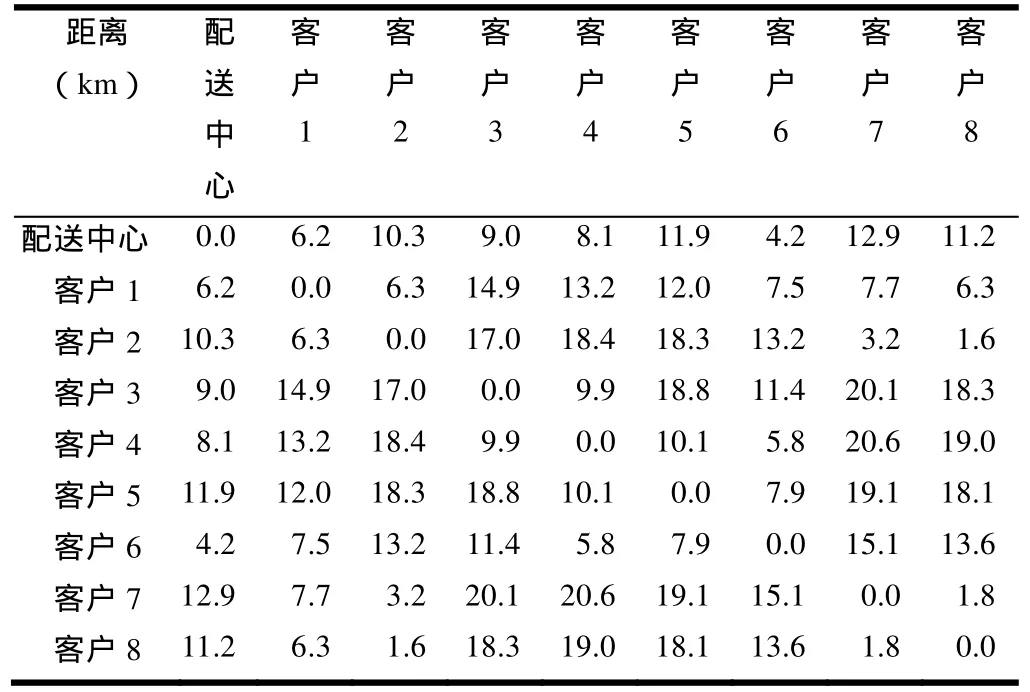
表2 实验样本1的配送中心与客户间的距离

第一组实验分别采用100次迭代的爬山算法、粒子群算法算法、改进粒子群算法、动态规划法解决规模较小的实验样本1问题。实验结果如表3所示。

第二组实验分别采用1000次迭代的爬山算法、粒子群算法算法、改进粒子群算法、动态规划法解决规模较大的实验样本2问题。实验结果如表4所示。

实验中，各算法运行 20次进行统计，将平均数据作为实验结果。

表3 实验样本1实验结果

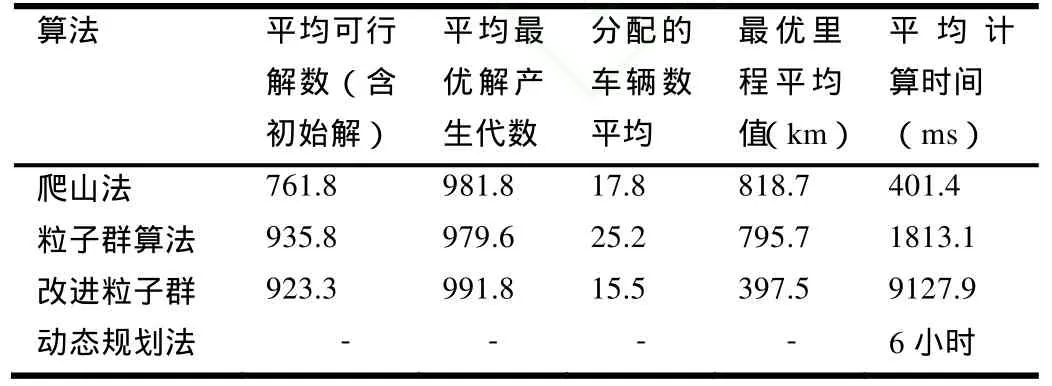
表4 实验样本2实验结果

从数据中可以看出，对于规模较小的实验样本1，改进粒子群算法生成的调度方案的最小总里程为66.4km，优于改进前的粒子群算法，但是计算结果不如爬山法和动态规划法。动态规划法是精确算法，计算产生了最优化结果，最小总里程为54.1km。

对于规模较大的实验样本 2，改进粒子群算法生成的调度方案的最小总里程为 397.5km，明显优于爬山法和改进前的粒子群算法。由于改进粒子群算法由于相对复杂，耗时也相对较多，但计算时间属于实际应用可接受的范围内。动态规划法经6小时的计算没有生成最优化调度序列。实验证明动态规划法不适用于解决较大规模的物流配送车辆调度问题。

5 结束语

本文参照经典车辆路径问题模型，考虑了车辆配送里程和用户数等限制，建立了双向车辆调度问题的数学模型。在标准粒子群算法的基础上，引入爬山操作，增加了粒子群的多样性，提高了算法的局部搜索能力，并设计了基于改进粒子群算法的物流配送车辆调度算法。

通过分析和实验验证，得出如下结论：本文的改进粒子群算法可以有效地解决了物流配送车辆的优化调度问题。算法能够根据客户位置、配送车辆能力，综合协调，生成配送总里程优化的配送车辆调度方案。引入爬山操作增强粒子群算法的局部搜索能力，是算法改进的一项有效途径。

[1]Gilbert Laporte.Fifty Years of Vehicle Routing.Transportation Science, 2009 , 43(4)

[2]Pinedo M.调度：原理、算法和系统(第2版).张智海,译.北京：清华大学出版社，2007.

[3]张军,詹志辉.计算智能.北京:清华大学出版社,2009.

[4]王凌,刘波.微粒群优化与调度算法.北京:清华大学出版社,2008.

[5]Kennedy J, Eberhart R.Particle swarm optimization[C].In Proceedings of IEEE International Conference on Neural Networks,1995：1942-1948.

[6]Clerc,M.Discrete Particle Swarm Optimization, illustrated by the Traveling Salesman Problem.New optimization technique in engineering[C].Springer- Verlag,2004.

[7]Salmen A, Ahmad I, Al-Madani S.Particle swarm optimization for task assignment problem[J].Microprocessors and Microsystems,2002,26：367-371.

[8]Y Shi, R C Eberhart.Empirical study of particle swarm optimization.In Proceedings of the Congress on Evolutionary Computation,1999:1945-1950.