长航时捷联惯导重力扰动影响及补偿

丛 琳，赵 忠，杨小步

CONG Lin,ZHAO Zhong,YANG Xiaobu

西北工业大学 自动化学院，西安 710129

School of Automation,Northwestern Polytechnical University,Xi’an 710129,China

1 引言

捷联惯导系统的误差随时间积累，在要求持续工作几十个小时以上的长航时惯性导航系统中这一特性表现得尤为突出。一些在短航时内忽略掉的惯导误差源随着高精度惯性器件的发展和工作时间的延长而引起惯导系统较大的误差，并成为主要的误差源，重力扰动就是其中一项[1-5]。在传统导航解算时通常采用正常重力作为重力有害加速度的补偿，在惯性器件精度不高的情况下，重力扰动的影响可以忽略[6-7]。但随着高精度惯导系统的发展，惯性元件陀螺和加速度计自身的精度得到了极大的提高，在长时间航行的高精度惯性导航系统中由重力扰动导致的惯导误差已经成为了惯性系统中最主要的误差源[8]，必须要进行重力扰动补偿。Vanderwerf等[9]分析了在重力扰动很大的航线上其对惯导的影响，但仅验证了速度误差的影响；尧颖婷等[10]验证了重力扰动的水平分量对捷联惯导误差的影响，但并没有对重力扰动进行补偿；李胜全等[11]仿真分析重力扰动矢量补偿对惯导精度的提高效果，但假设重力异常与垂线偏差为均匀分布，且补偿后的重力扰动为常值，这个假设条件太过理想。本文从导航解算的角度出发，分析长航时捷联惯导系统误差受重力扰动的影响，在此基础上对重力扰动进行非均匀B样条建模并对导航解算过程进行补偿，仿真结果表明了非均匀B样条建模的正确性以及重力扰动补偿的有效性。

2 重力扰动对捷联惯导影响

重力作为惯导系统有害加速度通过加速度计感测进入惯导系统，在导航解算中，重力补偿之后的残余重力将产生惯导误差，系统残余重力可表示为实际重力与正常重力之差，即为重力扰动：

式中，g为实际重力，γ为正常重力，δg为重力扰动。本文从捷联惯导解算更新出发，分别分析了重力扰动对姿态、速度和位置的影响。

导航坐标系（n系）选用地理坐标系东、北、天（ENU）；b为载体坐标系；i是惯性坐标系；e表示地心地固坐标系。

2.1 捷联惯导姿态误差分析

在捷联惯导姿态更新中，根据文献[12]可知姿态误差方程为：

式中δKG为陀螺刻度系数误差，δG为陀螺安装角误差，ϕ表示姿态角误差为坐标系转换矩阵，为陀螺输出，εn为陀螺漂移在导航坐标系中的投影，为指令角速度误差，且：

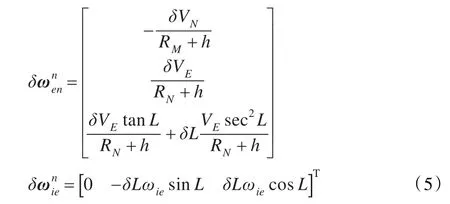
式中L为所在地的纬度，RM、RN、h依次为载体所在地的子午圈半径、卯酉圈半径和海拔高度。

根据式（2）可知，引起姿态误差的主要误差源有陀螺输出误差，除陀螺误差之外的误差源是通过速度位置的耦合关系而作用于姿态的，表现于项。现从捷联惯导速度更新的速度误差源进行分析。

2.2 捷联惯导速度更新误差分析

捷联惯导解算时系统的速度更新误差方程为：

式中，δKA为加速度计刻度系数误差，δA为加速度计安装角误差，fn表示加速度计输出，∇n为加速度计零偏在导航坐标系下的投影，δgn为重力扰动。

由式（6）可知，引起捷联惯导系统速度误差的误差源主要有加速度计输出误差([δKA]+[δA])fn+∇n，前一时刻累积的速度误差δVn，速度位置的耦合误差以及重力扰动δgn的影响。

2.3 捷联惯导位置更新误差分析

捷联惯导解算时系统的位置更新误差方程为：

式中L、λ分别为地理纬度和经度。

由式（8）可知，引起位置误差的主要误差源为前一时刻的累积速度误差δVn以及速度位置的耦合误差。

经过上面分析可以发现：重力扰动可以通过式（6）引起捷联惯导的速度更新误差，速度误差将通过式（8）造成系统位置更新误差，进而通过式（2）引起捷联惯导系统的姿态误差，并且惯导误差随着时间的增加还会发散。

3 重力扰动补偿

根据前面的分析可以看出，在传统捷联惯导中，重力加速度的补偿是影响惯导精度的一个关键因素，一般可以根据地球正常重力模型得到的正常重力矢量进行补偿。但在长航时高精度捷联惯导系统中，重力扰动对惯导解算的影响不可忽略，必须针对重力扰动矢量进行重力补偿。

在进行重力扰动补偿的时候，需将其分解到北向、东向和垂向。北向分量和东向分量可用垂线偏差表示，即

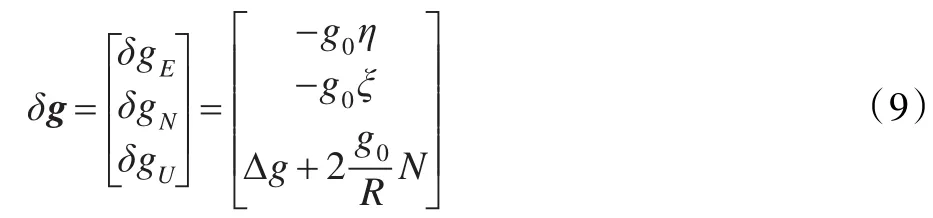
式中ξ为南北方向垂线偏差，η为东西方向垂线偏差，g0为正常重力值，Δg为重力异常，N为水准面高度，R为地球半径。

重力异常Δg通过比力方程进入惯导系统后作用于系统的高度通道，对水平定位精度影响不大[13]，且由于高度通道是发散的，则在捷联惯导系统中，重力异常的影响一般可忽略不计[14]。而垂线偏差对水平方向的定位误差影响较大，一般地区的垂线偏差在10″左右，个别地区可以达到30″以上[15]，这在惯导系统中引起的水平位置误差在百米甚至千米以上，因此需要对其进行全面分析及补偿。下文的重力扰动补偿指的是对垂线偏差的补偿。

重力扰动补偿是在垂线偏差模型的基础上对重力扰动的补偿。在实际导航中，实时测量所有导航点的垂线偏差是不实际的，所以需要根据已知点的垂线偏差运用插值补偿算法或其他算法估测未知点的垂线偏差，辅助惯性导航。而重力扰动在实际中的分布往往是不规则的，需要非均匀网格数据。所以本文采用非均匀B样条最小二乘法对局部计算区域垂线偏差进行二维整体逼近，此方法能保证在垂线偏差局部特性不失真的前提下获得计算区域垂线偏差的统一解析式，同时解得的垂线偏差具有连续性。

3.1 非均匀B样条最小二乘法

对于二维区域[0 ≤x≤a，0≤y≤b]，在 x方向插入等分节点：Δx:0=x0＜x1＜…＜xn=a。那么，在 x方向上的B样条函数[16]可表示为：

式中 Bi，μ(x)为B样条基函数，可表示为：

从式（10）（11）中可以看出，B样条函数在每段区间上的部分只与相邻部分控制顶点有关，某一控制顶点的变动只会造成局部形状的变化，并不会影响整体的模型变动，这样，各段曲线就具有了相对的独立性。

同理，在 y方向上插入等分点Δy:0=y0＜y1＜…＜yn=b。在 y方向的B样条函数为：

那么，二维区域xy平面的B样条[17]可写成Bx与By的张量积形式：

此时，根据已知节点矢量和数据点的参数值，通过式（13）便可以建立非均匀B样条模型S(x，y)，全体 S(x，y) 即构成一个线性空间，接下来就可以求解未知控制顶点的线性最小二乘问题了，即在此空间中找出合适的S(x，y)使得其满足：

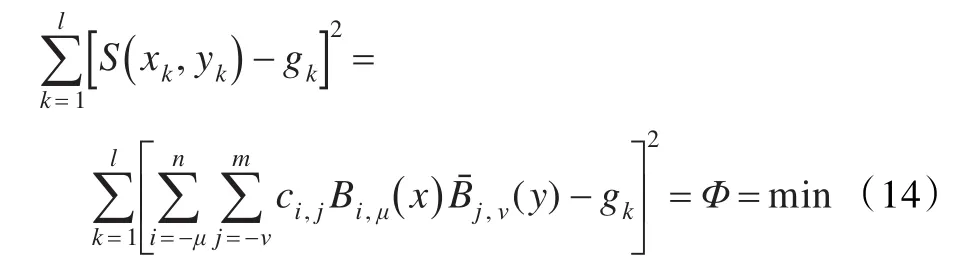
式中gk为实际得到的垂线偏差数据。即运用最小二乘法，令：

整理后可得：

求取范数极小解 ci，j，将得到的唯一系数 ci，j带入到式（13）中即为所求的非均匀B样条模型。

3.2 重力扰动补偿

运用上述非均匀B样条最小二乘法计算得到的重力扰动δg，补偿到原系统比力方程中再进一步进行导航解算，其原理流程简图如图1所示。

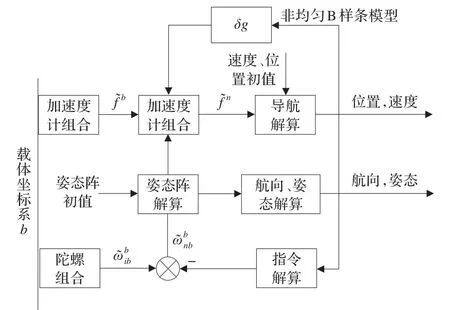
图1 导航解算原理图

4 仿真分析

4.1 重力扰动建模仿真

仿真条件：仿真模拟区域数据来自美国国家大地数据测量局提供的美国本土24°～58°N、230°～300°E，1'×1'的垂线偏差网格数据，根据已知数据可得真实垂线偏差如图2，表1所示。

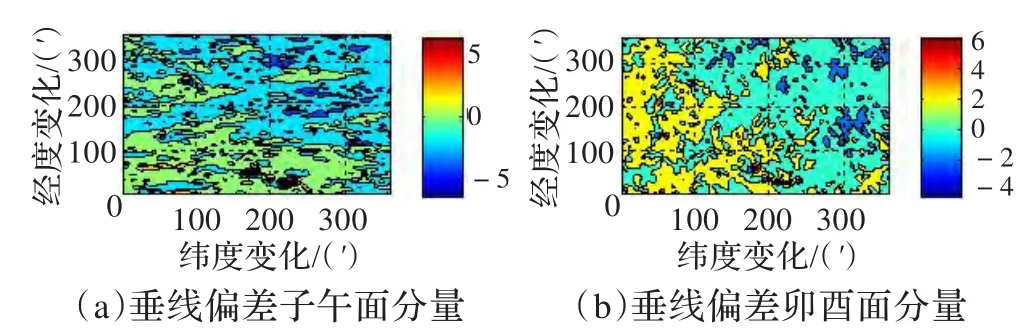
图2 垂线偏差变化各向分量

表1 垂线偏差真实值

采用B样条建立模型时，将模拟区域分成9个小区，各区选择30个点来保证已知点尽量分散，采用非均匀B样条进行仿真，所得各向垂线偏差如图3，表2所示。

图3 采用B样条建模垂线偏差变化各向分量

表2 采用B样条建模计算垂线偏差值

利用模型计算值对真实值进行补偿，所得误差如图4，表3所示。

图4 B样条建模补偿后垂线偏差误差

表3 补偿后垂线偏差误差值

由仿真结果可以发现：未经重力补偿时垂线偏差真实值最大可达到7″左右，当采用非均匀B样条最小二乘法建模时，垂线偏差各向分量与真实值相近，将非均匀B样条建模得到的垂线偏差与真实垂线偏差值进行补偿求差后，误差极值仅在1″左右，有较好的重力补偿效果，说明采用非均匀B样条方法可以对局部区域垂线偏差进行二维整体逼近，在局部特性不失真的情况下具有连续性。此方法的补偿精度明显高于文献[18]中采用的EGM2008（2 190阶）模型计算出来的垂线偏差精度，说明采用非均匀B样条进行重力扰动建模是非常有效的。

4.2 重力扰动对惯导补偿仿真

仿真条件：陀螺常值漂移0.001（°）/h，随机游走系数为0.000 2（°）/h，加速度计常值偏置为10×10－6g，零均值白噪声为5×10－6g，导航解算周期为0.02 s，无初始对准误差，仿真过程中可忽略掉高度通道的影响，即δh=0。仿真时长为24 h。仿真中利用提供的1'×1'网格数据插值后得到网格区域内的垂线偏差数据来模拟实际重力扰动，加入到惯导系统中可以得到无重力扰动补偿时捷联惯导误差如图5所示。采用上述非均匀B样条补偿的方法，进行重力扰动补偿后，可以得到捷联惯导系统误差如图6所示。

图5 无重力扰动补偿惯导系统误差

图6 重力扰动补偿后惯导系统误差

由仿真结果可以发现：未经重力扰动补偿的导航解算所得到的位置误差范围为-480～330 m，采用B样条重力扰动补偿后，导航定位精度有了明显提高，位置误差范围缩减到-210～210 m，同时速度误差也有了明显地减小，由此可以看出重力扰动造成的惯导位置误差最大可以达到200 m以上，这与惯性器件造成的误差基本达到了一个量级，所以必须要进行重力扰动补偿。此方法明显优于文献[19]中提到的直接线性插值重力补偿方法。由以上分析可以说明，采用非均匀B样条方法进行重力扰动补偿可更有效地提高惯导精度。

5 结束语

（1）随着高精度惯性器件的发展以及惯导工作时间的延长，重力扰动会引起较大的惯导误差，成为捷联惯导系统的主要误差源，必须要对其进行适当补偿，以保证惯导系统在较高的精度范围内工作。

（2）在进行重力扰动补偿时，无法精确获得所有点的垂线偏差数值，需要建立相关的重力扰动模型，采用非均匀B样条方法可以保证在垂线偏差局部特性不失真的前提下进行二维整体逼近，利用所求重力模型对惯导系统补偿可以有效地提高惯导精度。

[1]吴太旗.重力场对惯性导航定位误差影响研究与仿真[J].测绘科学技术学报，2006，23（5）：341-344.

[2]李斐，束蝉方，陈武.高精度惯性导航对重力场模型的要求[J].武汉大学学报：信息科学版，2006，31（6）：508-511.

[3]Hsu D Y.An accurate and efficient approximation to the normal gravity[C]//IEEE Position Location and Navigation Symposium，1998：38-44.

[4]卢鑫，练军想，吴美萍.高精度舰载惯性导航系统的重力影响研究[J].导航与控制，2010，9（4）：15-21.

[5]陈永冰，边少锋，刘勇.重力异常对平台式惯性导航系统误差的影响分析[J].中国惯性技术学报，2005，13（6）：21-25.

[6]Kriegsman B A，Mahar K B.Gravity-model errors in mobile inertial-navigation systems[J].Journal of Guidance and Control，1985，15.

[7]Moryl J，Rice H，Shinners S.The universal gravity moduleforenhanced submarinenavigation[C]//IEEE Position Location and Navigation Symposium，1998：324-331.

[8]Jekeli C.Inertial navigation systems with geodetic applications[M].Berlin：deGruyter，2001：200-230.

[9]Vanderwerf K.Schuler pumping of inertial velocity errors due to gravity anomalies along a popular north pacific airway[C]//IEEE Position Location and Navigation Symposium，1996：642-648.

[10]尧颖婷，沈晓蓉，邹尧，等.捷联惯性导航系统重力扰动影响分析[J].大地测量与地球动力学，2011，31（6）：159-163.

[11]李胜全，欧阳永忠，常国宾，等.惯性导航系统重力扰动矢量补偿技术[J].中国惯性技术学报，2012，20（4）：410-413.

[12]秦永元.惯性导航[M].北京：科学出版社，2006：358-361.

[13]Rogers R M.Applied mathematics in integrated navigation system[M].New York：American Institute of Aeronautics and Astronautics，2007：20-40.

[14]吴太旗，黄谟涛，边少锋.高精度惯性导航系统的重力场模型影响模式分析[J].测绘通报，2009，5（5）：5-8.

[15]Haxby W F.Gravity filed of the world’s Oceans[R].US：Navy Naval Office of Research，1985.

[16]郭建锋，归庆明，杨元喜.局部重力场的非均匀B样条最小二乘逼近[J].测绘学报，2000，29（3）：189-192.

[17]宁津生，定波，边少锋.重力场的样条逼近[J].测绘学报，1990，19（4）：241-249.

[18]齐显峰，周巍，崔吉春.EGM2008重力场模型计算中国地区垂线偏差分析[J].测绘技术装备，2011，13（1）：6-8.

[19]卢鑫.长航时高精度惯性导航系统重力补偿技术研究[D].长沙：国防科技大学，2010.