基于智能算法的土壤环境质量PPC评价模型的比较研究

何厅厅，赵艳玲，侯占东，曾继勇，李 源，王亚云，刘亚萍

(中国矿业大学(北京)土地复垦与生态重建研究所，北京 100083)

土壤环境质量评价是研究土壤环境质量变化基础工作，通过土壤环境污染指数动态变化来反映。目前，关于土壤环境质量评价的方法很多，例如灰色聚类法[1]、综合指数法[2]及BP神经网络法[3]等，这些方法各有特征，但模型精度难以控制。土壤环境质量评价实质上是依据污染物浓度分级标准对待评单位进行污染级别分类，它涉及到不同属性的多个指标，是一种复杂的高维数据非线性分类问题。投影寻踪聚类[4](Projection Pursuit Cluster，简称PPC)模型，采用“审视数据—模拟—预测”探索性数据分析的途径，有效地解决了多指标样本分类等非线性分类问题，并能避免“维数祸根”[5]。然而，对于具有复杂拓扑结构的多元数据，一般难以找到最佳投影方向[6]，且计算量大。本研究利用群体智能算法在函数寻优的优势，将细菌算法(BFA)、遗传算法(GA)、鱼群算法(FSA)与PPC模型结合，提出土壤环境质量评价的BFA-PPC、GA-PPC、FSA-PPC模型，并进行实例研究，分析各模型的优异程度。

1 土壤环境质量评价的PPC模型

1.1 PPC模型

投影寻踪(Projection Pursuit，PP)是一种有效的高维数据分析和处理的统计方法，尤其实用于非线性、非正态分布的高维数据处理[7-8]。其基本思想：利用计算机技术，通过某种组合，将高维数据投影到低维子空间上，形成具有整体分散和局部凝聚特征的新目标指标，即投影值，分析低维空间投影值特征，达到处理多因素复杂问题的统计方法。PPC模型就是根据投影寻踪思想建立的一种聚类模型，在多因素评价、聚类、优选等方面得到了广泛应用[9-12]。其中，投影指标函数的构造、优化方法的选择是应用PPC分类方法能否成功的关键。群体智能算法常用于函数寻优，引入细菌算法(BFA)、遗传算法(GA)、鱼群算法(FSA)，构建土壤环境质量评价的BFA-PPC、GA-PPC、FSA-PPC模型。具体的建模步骤如下所示[10-11]。

步骤一：评价指标的归一化处理。

已知土壤重金属指标样本{x′(i,j)|i=1,2,…,n;j=1,2,…,p}。其中：x′(i,j)为第i个样本第j个指标值；n，p分别为样本个数(样本容量)和评价指标数目。为消除各评价指标值的量纲和统一各评价指标值的变化范围，对x′(i,j)进行归一化处理，见式(1)。

(1)

式中xmax(j)为第j个指标值的最大值。

步骤二：构建投影指标函数Q(a)。

PP法就是把p维数据{x′(i,j)|i=1,2,…,n;j=1,2,…,p}综合成以单位向量a={a(1),a(2),…,a(p)}为投影方向的一维投影值z(i)，见式(2)。

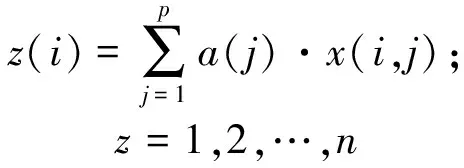
(2)

根据{z(i)|i=1,2,…,n}的一维散布图进行分类与评价。

综合投影指标值时，要求投影值z(i)的散布特征为局部投影点尽可能密集，最好凝聚成若干个点团；而在整体上投影点团之间尽可能散开。故投影指标函数可以表达为式(3)。

Q(a)=Sz·Dz

(3)

式中，Sz为投影值z(i)的标准差，Dz为投影值z(i)的局部密度。

(4)

(5)

式中，E(z)为序列{z(i)|i=1,2,…,n}的平均值；R为局部密度的窗口半径，它的选取既要使包窗口内的投影点的平均个数不太少，避免滑动偏差太大，又不能使它随着n的增大而增加太大，R可以根据试验来确定，一般可取值为0.1Sz；z(i)表示样本之间的距离，r(i,j)=|z(i)-z(j)|;函数u为一单位阶跃函数，当t>0其值为1，当t<0时，其函数值为0。

步骤三：优化投影指标函数。

当各指标值的样本集给定时，投影指标函数Q(a)只随着投影的方向a的变化而变化。不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向，因此，可以通过求解投影指标函数最大化问题来估计最佳投影方向，见式(6)、式(7)。

max:Q(a)=Sz·Dz

(6)

(7)

这是一个以{a(i)|i=1,2,…,p}为优化变量的复杂非线性优化问题，用传统的优化方法处理较难。因此，应用群体智能算法中的遗传算法、细菌算法和鱼群算法来解决其高维全局寻优问题，从而可以得到最佳投影方向a。

步骤四：分类和优序排列。

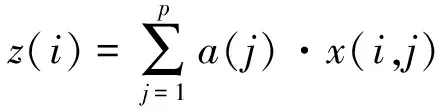
1.2 群体智能算法

1.2.1 细菌算法

细菌算法[13-15](Bacterial Foraging Algorithm，BFA)是分布式最优化控制领域提出的一种新的优化算法，其受细菌在化学引诱剂环境中运动行为的启发而提出的。算法主要依靠以细菌特有的趋化、繁殖、迁徙三种行为为基础的三种算子进行位置更新和最优解的搜索，进而实现种群的进化。该算法具有简单性和鲁棒性，随机搜索能力强。具体的流程如图1。

1.2.2 遗传算法

遗传算法[16-17](Genetic Algorithm，GA)是基于生物进化过程中优胜劣汰与群体内部染色体信息交换而形成的一种解决最优问题的概率搜索算法。主要包括选择、交叉和变异。如图1所示。

1.2.3 鱼群算法

鱼群算法[18-19](Fish Swarm Algorithm，FSA)是一种模拟鱼群运动规律的优化算法，其基本思想是鱼群向食物浓度较大的水域游动，鱼群规模最大的地方食物浓度最大。据此，鱼群算法构造人工鱼个体，模拟鱼群的觅食、群聚和追尾行为，通过个体的局部寻优，实现全局最优。该算法具有操作简单、收敛快速、全局搜索能力强的特点。如图1所示。

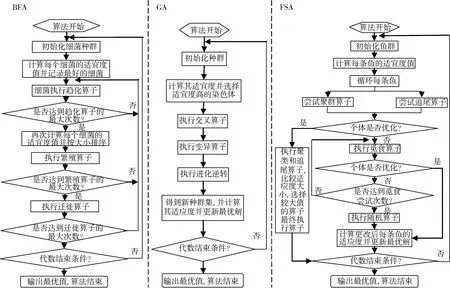
图1 3种群体智能算法流程

2 实例分析

基于上述理论模型和群体智能算法，以某地区农业土壤重金属污染为例，应用PPC模型进行土壤环境质量评价，同时比较三种群智算法优异性。选取对土壤影响较大的镉、汞、铅、铬、铜、锌等六种重金属作为环境质量的评价指标，实测数据和评价分级标准数据参见文献[3]，利用式(1)，对实测数据和分级标准进行归一化处理，见表1。

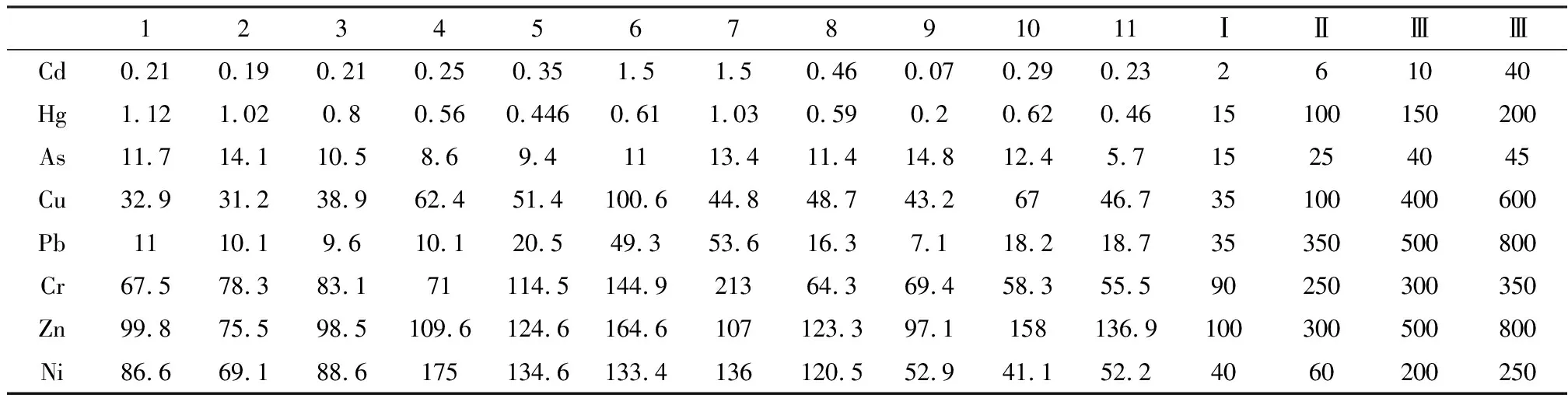
表1 实测数据和分级标准归一化

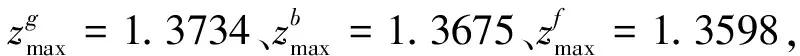
根据BFA算法、GA算法、FSA算法的最佳投影方向和表1，利用公式(2)，算得实测数据和分级标准数据的投影值为：zb={0.0904，0.0975，0.0947，0.1104，0.1502，0.2697，0.2709，0.1216，0.1107，0.1433，0.06，000.1857，0.9561，1.7034，2.6272}，zg={0.0801，0.0891，0.0844，0.0958，0.1333，0.2408，0.2527，0.1054，0.0971，0.121，0.0487，0.1834，0.9563，1.6585，2.5749}，zf={0.0692，0.0731，0.0719，0.086，00.1158，0.2224，0.2104，0.0963，0.0848，0.1191，0.0522，0.1648，0.9113，1.612，2.5333}。将样品1～11的投影值和标准数据的投影值进行比较，得到3种评价模型下样品1～11的污染级别均为{Ⅰ，Ⅰ，Ⅰ，Ⅰ，Ⅰ，Ⅱ，Ⅱ，Ⅰ，Ⅰ，Ⅰ}。

为了分析3种评价模型的优异性，将其对应的分级标准投影值分别和分级参数{Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ}进行二次多项式拟合，如图4。将原始数据投影值分别代入对应的拟合函数，得到在不同模型下各样品的污染级别拟合值如表5所示。

由表5可知，BFA、GA、FSA优化PPC模型，土壤环境质量评价结果基本保持一致。样品1，Cd、Hg、As、Cu、Pb、Cr、Zn均低于Ⅰ级标准，占87.5%的指标，仅Ni在Ⅱ-Ⅲ级之间，故定为Ⅰ级合理，同理，样品2、3为Ⅰ级。样品4、5的指标62.5%低于Ⅰ级标准，25%在Ⅰ-Ⅱ级，12.5%在Ⅱ-Ⅲ级，且样本5中的87.5%指标高于样本4，与其拟合值递增吻合。样本6，37.5%指标低于Ⅰ级，37.5%高于Ⅰ级，25%在Ⅱ-Ⅲ级，其中Cu微高于Ⅱ级，定为Ⅱ符合实际情况。样品7，Cu在Ⅰ-Ⅱ级，其他指标与样品6基本一致，可以认为，样品7为Ⅱ级，但污染程度低于样品6。样品8、9，由上文分析，评定为Ⅰ级。

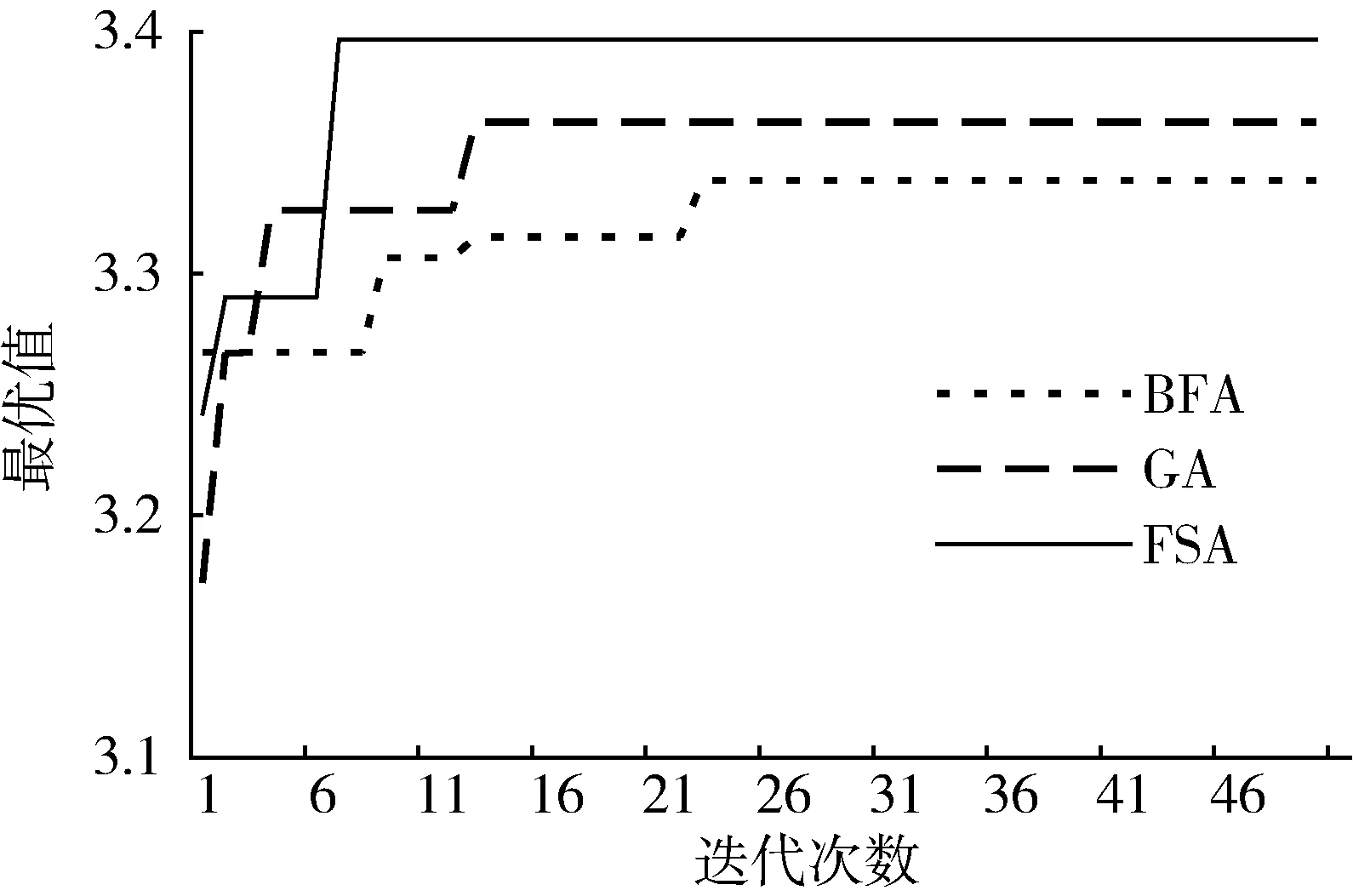
图2 3种群智能算法的寻优能力比较

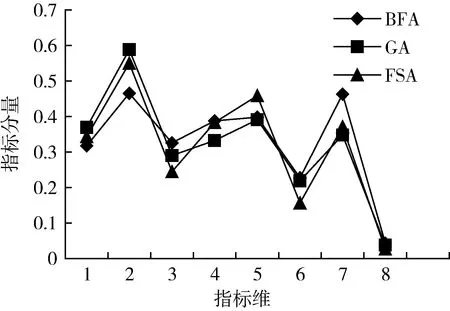
图3 最佳投影方向

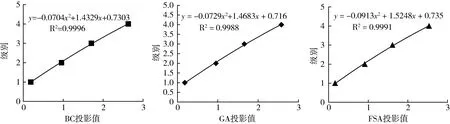
图4 标准投影值的拟合曲线

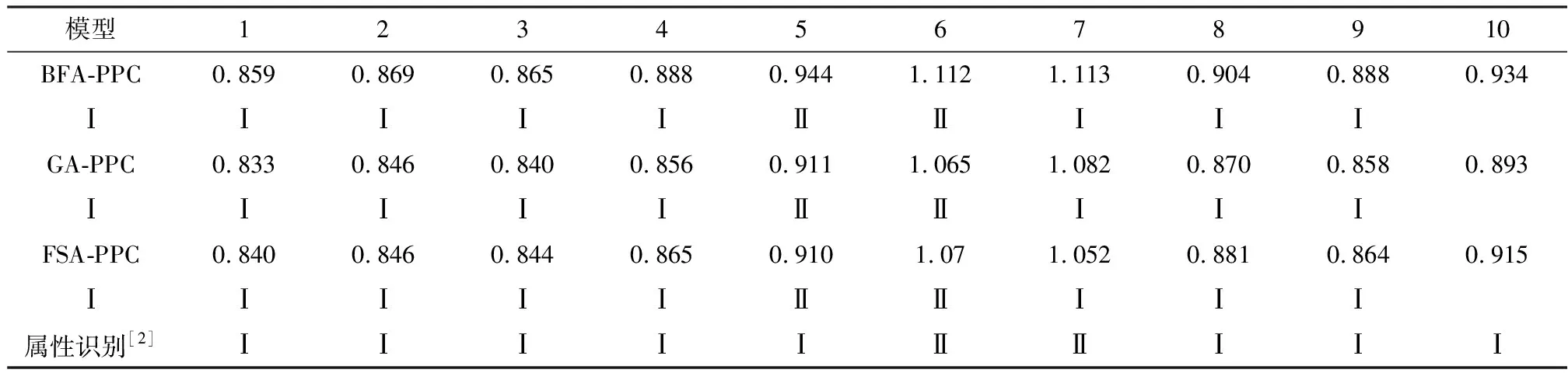
表5 土壤环境质量评价结果

综上所述，PPC模型在土壤环境质量评价中的应用，结果表明，该模型是科学与合理的。3种群智算法用于该模型测算结果基本保持一致，说明：3种群智算法均能用于PPC模型计算最佳投影方向的有效方法，且其优异程度：BFA

3 结论

1) 本文应用智能算法优化的PPC模型应用于土壤环境质量评价，通过PPC模型将多维指标的重金属数据转化为一维数据，避免了人为赋权的主观性，利用智能算法获取最优投影方向，并由最优投影值算得各样品的污染等级，通过实例分析，并将评价结果与传统的属性识别综合评价法的评价结果进行比较分析，表明：基于智能算法的土壤环境质量PPC评价模型是一种有效的土壤环境质量分析方法。

2) 通过对3种智能算法优化土壤环境质量PPC评价模型的实例分析知，在土壤环境质量PPC评价模型中，FSA的优化结果最好，其次是GA、BFA，由图1、图2可知，3种智能算法的寻优能力及其算得最佳投影方向优异程度均为：BFA

[1] 李雪梅,王祖伟,汤显强,等.重金属污染因子权重的确定及其在土壤环境质量评价中的应用[J].农业环境科学学报,2007,26(6):2281-2286.

[2] 徐友宁,陈社斌,陈华清,等.大柳塔煤矿开发土壤重金属污染响应研究[J].中国矿业,2007,16(7):47-54.

[3] 孔健健,张阳,张江山.属性识别理论模型应用于土壤重金属污染评价[J].环境工程,2012,30(1):100-102,105.

[4] 赵玉杰,师荣光,高怀友,等.基于MATLAB6.x的BP人工神经网络的土壤环境质量评价方法研究[J].农业环境科学学报2006,25(1):186-189.

[5] 王顺久,倪长健.投影寻踪动态聚类模型及其应用[J].哈尔滨工业大学学报,2009,41(1):178-180,184.

[6] 汪明武,金菊良,李丽.投影寻踪新方法在泥石流危险度评价中的应用[J].水土保持学报,2002,16(6):79-81.

[7] 万中英,廖海波,王明文.遗传-粒子群的投影寻踪模型[J].计算机工程与应用,2010,46(20):210-212,240.

[8] Platje A,Seidel H,Wadman S.Project and portfolio planning cycle-project based management for multi-project challenge[J].International Journal of Project Management,1994,12(2):100-105.

[9] Leu SouSen,Chen AnTing,Yang ChungHuei.A GA-based fuzzy optimal model for construction time-cost trade-off[J].International Journal of Project Management,2001,19(1):47-58.

[10] 黄晓荣,付强,梁川.投影寻踪分类模型在工程评标中的应用[J].哈尔滨工业大学学报,2001,36(1):69-72.

[11] 黄晓荣,梁川,付强,等.基于RAGA的PPC模型对区域水资源可持续利用的评价[J].四川大学学报:工程科学版,2003,35(4):29-32.

[12] 金菊良,汪明武,魏一鸣.用投影寻踪分类模型进行环境监测优化布点[J].安全与环境学报,2004,4(4):10-12.

[13] WANG S J,ZHANG X L,YANG Z F,et al.Projection

pursuit cluster model based on genetic algorithm and its application in Karstic water pollution evaluation[J].International Journal of Environment and Pollution,2006,28(3-4):253-260。

[14] 周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用，2010,46(10):19-20.

[15] Das S,Biswas A,Dasgupta S,et al.Bacterial foraging optimization algorithm:Theoretical foundations,analysis,and applications[J].Foundations of ComPuteIntel,2009,3:23-55.

[16] Chen H,Zhu Y,Hu K.Cooperative bacterial foraging optimization.Discrete Dynamics in Nature and Society.2009:1-17.

[17] Mika M,Waligóra G,Weglarz J.Tabu search for multi-mode resource-constrained project scheduling with schedule-dependent setup times[J].European Journal of Operational Research，2008,187(3):1238-1250.

[18] Kim K W,Yun Y S,Yoon J M.Hybrid genetic algorithm with adaptive abilities for resource-constrained multiple project scheduling[J].Computers in Industry,2005,56(2):143-160.

[19] 杨淑霞,韩奇,徐琳茜,等.鱼群算法与神经网络结合的节能减排效果评价[J].中南大学学报：自然科学版,2012,43(4):1538-1544.

[20] Saeed F.Efficient job scheduling in grid computing with modified artificial fish swarm algorithm[J].International Journal of Computer Theory and Engineering,2009,1(1):13-18.

[21] 周利民.基于鱼群算法的无线传感器网络覆盖优化研究[D].长沙：湖南大学,2010.