河南省城市科技效率评价研究
2014-04-01刘绘珍
刘绘珍
(郑州航空工业管理学院 管理科学与工程学院,河南 郑州 450015)
科技是社会第一生产力,近现代的发展史和各种经济理论都表明:科技是一国或地区经济发展和社会进步最主要的动力和源泉。2012年11月,党的十八大提出要实施创新驱动发展战略,提出要坚持走中国特色自主创新道路,要用全球视野来谋划科技进步和创新。采用三阶段DEA(Data Envelopment Analysis,DEA)评价方法,选取2007年到2012年共6年数据,对河南省各城市科技投入产出进行评价研究,以使各城市认清自身在整个河南省中所处的位置,认识自身的优势和劣势,借鉴其他城市的成功经验,寻求提高自身科技效率的有效途径,为科技的管理和发展完善提供一些实践上可供参考的改进方向,同时为政府部门决策提供参考。
一、模型与变量选取
1.三阶段DEA方法
数据包络分析方法是运筹学发展的一个新领域,其方法和模型是由美国著名运筹学家A·Charnesh和W·W·Cooper等人以效率概念为基础发展起来的一种效率评价方法,它是研究若干相同类型的具有多输入、多输出的部门(或单元)间相对有效的方法。DEA本质是判断决策单元是否位于生产可能集的生产前沿面上,使用DEA方法和模型可以确定生产前沿面的结构、特征和构造方法。它主要采用线性规划方法,在将原始样本数据划分为输入指标和输出指标的基础上,对决策单元进行有效性评价,其目的是反映决策单元能否达到“以尽可能少的投入,获得最大效益”的决策结果。
传统DEA方法的不足是无法分离随机因素和测量误差的影响。使用三阶段DEA方法,可以克服传统DEA方法本身的局限性,剔除随机误差的影响。同时还可以分离环境变量对投入差额值的影响,提高所选决策单元的同质性,测度出更加准确、真实的科技效率。还可以更进一步确定相对无效决策单元主要是技术无效还是规模无效。
三阶段DEA方法的思想如下:
第一阶段:传统的DEA模型(BCC模式)。Banker、 Charnes和Cooper在1984年提出了BCC模式,把技术效率分解为规模效率和纯技术效率,即,技术效率=规模效率×纯技术效率。纯技术效率反映的是DMU 在一定( 最优规模时) 投入要素的生产效率。规模效率反映的是实际规模与最优生产规模的差距。技术效率是对决策单元的资源配置能力、资源使用效率等多方面能力的综合衡量与评价。
第二阶段:建立SFA模型。第一阶段在得出效率值的同时还得到各决策单元的投入差额值,该差额值即为被考察对象的实际投入与最佳效率下的投入之差。投入差额同时受到了环境因素、随机误差以及内部管理三个因素的影响,因而利用SFA剥离环境因素、随机误差对该值的影响。设有k个决策单位,每个决策单位均使用n种投入Xnk,其差额为Snk;p个可观察环境变量Zk=[z1k,z2k,…,zpk]。根据Battese和Coelli(1989)的研究,差额变量和环境变量的回归方程为:
Snk=fn(Zk,βn)+Enk
(1)
Enk=Vnk+Unk
(2)
其中,β为环境变量的待估参数;fn(Zk,βn)表示环境变量对投入差额值Snk的影响方式,一般取fn(Zk,βn)=Zk×βn;Vnk+Unk为复合误差项,Vnk表示随机干扰,并假设Vnk正态分布,Unk表示管理无效率,并假设 Unk服从截断正态分布;Vnk与Unk相互独立。
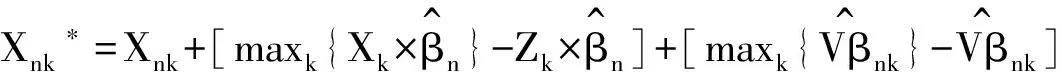
(3)
第三阶段:调整的DEA模式。在第三阶段,将第二阶段得出的调整后投入值与原始产出值再次代入DEA模型,计算各决策单位的效率。这时所得到的即为消除了环境因素和随机误差影响后的效率值。
2.样本和变量的选取
研究数据主要来源于河南省统计年鉴以及河南省各城市科技厅或统计局官方网站。本研究选取了河南省18个城市从2007年至2012年共6年的数据作为原始数据,共108个样本。
根据科学性、合理性、可比性、可获得性原则,参照《中国科技发展研究报告》中有关科技投入产出的评价指标体系,并结合当前社会经济及科技发展趋势,将科技投入产出指标和环境指标分别设计为:科技投入由科技活动人员、有研发活动的单位数和地方财政科技拨款总额构成;科技产出由专利申请数、出版科技著作和技术成交量构成;环境变量由人口数、城镇化水平、区域面积和GDP构成。
二、实证分析
1.第一阶段效率分析
(1)技术无效率的主要原因。整个河南省城市2007年到2012年的技术效率均值、纯技术效率均值和规模效率均值分别为0.47、 0.521和0.879,说明河南省城市技术无效的主要因素来自于纯技术效率。针对具体城市,比如,2012年鹤壁市的技术效率均值、纯技术效率均值和规模效率均值分别为0.711、 0.925和0.768,说明鹤壁市技术无效的主要因素来自于纯技术效率,因此该市需提高管理和技术等;2012年商丘市的技术效率均值、纯技术效率均值和规模效率均值分别为0.17、 0.17和0.996,说明商丘市技术无效的主要因素来自于规模效率,其改革的重点在于如何更好地发挥其规模效益。
(2)不同城市之间效率的比较。图1为河南省各城市技术效率降序排序,技术效率大于等于0.75的城市有郑州市、漯河市、洛阳市、鹤壁市和济源市,技术效率小于0.2的城市有周口市、驻马店市和三门峡市。
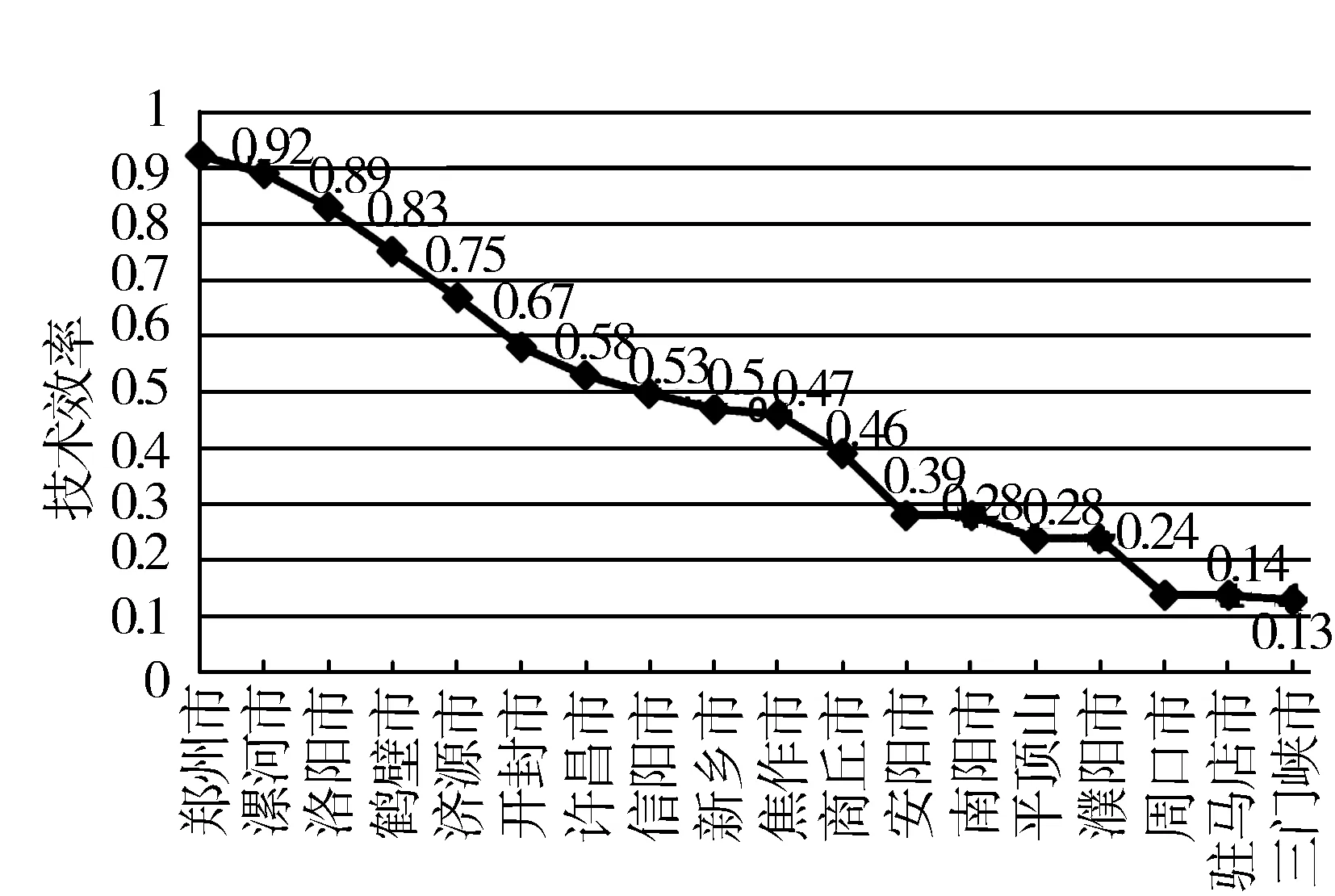
图1 第一阶段各城市技术效率
Fried、Lovell、Schmidt和Yaisawarng(2002)指出,企业的效率即可能受到内部管理的影响,也可能受到了所处的外部环境与随机误差的影响,前一个因素是内生的,后两个因素是外生的。DEA模型并不能剥离环境和误差因素对效率值的影响,因此,所得到的效率值并不能完全反映各城市的技术效率、纯技术效率和规模效率。
2.第二阶段SFA回归分析
针对3个投入差额,逐一用Frontier 4.1软件进行SFA分析,使用最大似然法估计回归系数,结果如表1、表2和表3。
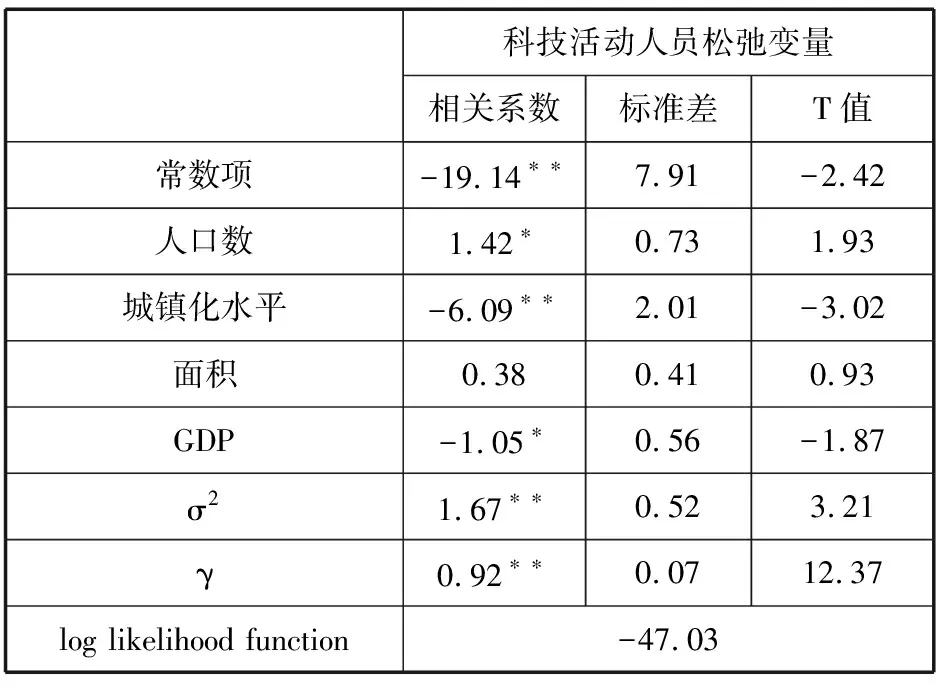
表1 科技活动人员SFA回归估计
表1、表2和表3显示:
(1)γ代表环境因素导致的差异变动在总变动中的比例,如果γ=0并在一定的显著水平下是显著的,那么代表由于环境因素导致的差异是不存在的,也就是我们使用的随机边界方程是不合适的。本研究使用t值检验回归方程的合理性, 表1、表2、表3中γ的t值全部通过了1%的显著性检验且最小值为0.68,可以看出环境因素的变动性解释了大部分的变动,也即是误差的变动影响因素很小。
(2)表1中,人口数、城镇化水平和GDP对科技活动人员松弛变量的影响通过了显著性检验。人口数对科技活动人员松弛变量的回归系数为正,说明人口数量庞大对科技活动人员松弛变量的减少是不利的。当经济发展到一定程度时,一个地方人口基数大,该地方人们的需求就会增多,就需要更多的科技人员来满足不同需求;同时由于现阶段河南省整体人力资源管理水平有限,所需要的科技人员在学科、受教育层次、个人素质等方面参差不齐,人数众多的科技人员就会因管理因素或个人因素造成人员浪费。城镇化水平对科技活动人员松弛变量的回归系数为负,说明城镇化水平的提高有利于科技活动人员松弛变量的减少。城镇化水平越高的地方,意味着这个地方的层次化教育、专业化教育等方面普及程度越高,越有利于科技活动的开展,因此,有助于减少科技活动人员的浪费。GDP对科技活动人员松弛变量的回归系数为负,说明GDP的增加有利于科技活动人员松弛变量的减少,即有利于减少科技活动人员的浪费或减低负产出。GDP总量越大,经济基础越雄厚,人们在教育、科普等方面的接受度越高,人们整体知识文化水平就越高,越有利于科技活动的开展,因此,有助于减少科技活动人员的浪费。

表2 有研发活动的单位数SFA回归估计
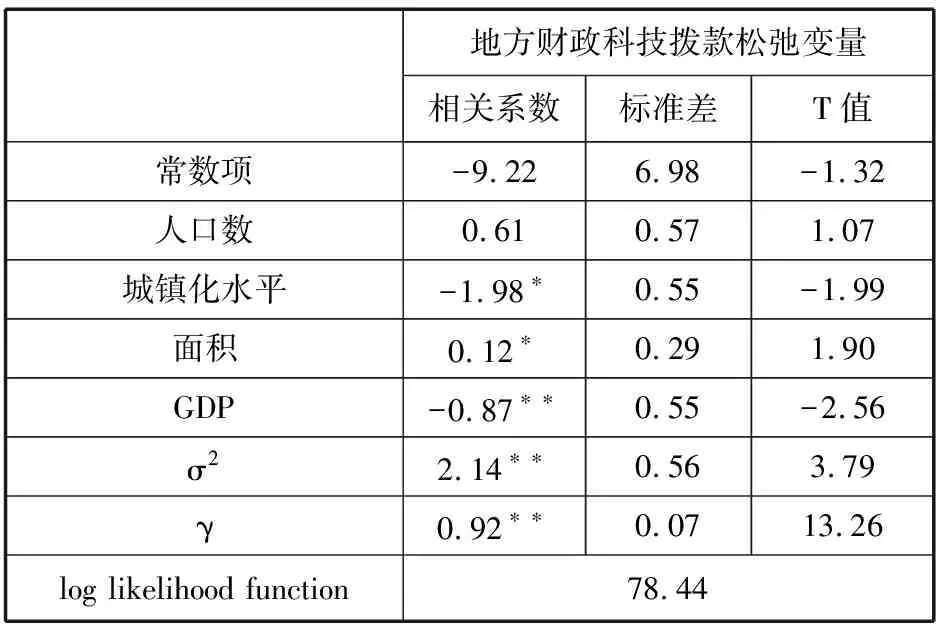
表3 地方财政科技拨款SFA回归估计
(3)表2中,只有城镇化水平对有研发活动的单位数松弛变量的影响通过了显著性检验。城镇化水平对有研发活动的单位数松弛变量的影响是负相关,即城镇化水平越高,有研发活动的单位数松弛度越小。城镇化水平代表一个地方的社会发展水平,在城镇化水平高的地方科技人力资源比较丰富,各种配套设施比较齐全,相当数量的企事业单位都把本企业的研发骨干(中心)配置在城镇化水平比较高的地方,因此,有利于有研发活动的单位效率的提高。
(4)表3中,城镇化水平、面积和GDP对地方财政科技拨款松弛变量的影响都通过了显著性检验。城镇化水平对地方财政科技拨款松弛变量的影响是负相关的,即城镇化水平越高,地方财政科技拨款松弛越小,城镇化水平高说明该地区的人们在层次化教育、专业化教育等方面普及程度很高,人们的综合素质比较高,所以城镇化有利于地方财政科技拨款使用效率的提高。区域面积对地方财政科技拨款松弛变量的影响是正相关,即地方面积越大,地方财政科技拨款的松弛度越大。因为地方辖区面积大,所辖的县市就越多,每个县市社会经济发展水平不同、科技实力不等、管理水平有高低;同时由于现阶段河南省整体管理水平有限,因此辖区面积使地方财政科技拨款浪费增大。GDP对地方财政科技拨款松弛变量的影响是负相关的,即地方GDP越大,地方财政科技拨款松弛度越小。地方GDP总量越高,说明该地方可以在基础教育、高等教育等领域投入更多的资金,人们接受更好的教育、综合素质更高,地方财政科技拨款效率将更高。
3.第三阶段效率分析
(1)技术无效率的主要原因。附表显示:整个河南省城市2006年到2012年的技术效率均值、纯技术效率均值和规模效率均值分别为0.443、 0.987和0.448,说明河南省城市技术无效的主要因素来自于规模效率。针对具体城市,比如,2012年济源市的技术效率均值、纯技术效率均值和规模效率均值分别为0.286、 0.99和0.288,说明济源市技术无效的主要因素来自于纯技术效率,因此该市需提高管理和技术等;2012年洛阳市的技术效率均值、纯技术效率均值和规模效率均值分别为0.961、 1和0.961,说明洛阳市技术无效的主要因素来自于规模效率,其改革的重点在于如何更好地发挥其规模效益。
(2)不同城市(区域)之间效率的比较。按照各城市技术效率降序排序得到图2,技术效率大于等于0.75的城市有郑州市和洛阳市,技术效率小于0.2的城市有鹤壁市和周口市。
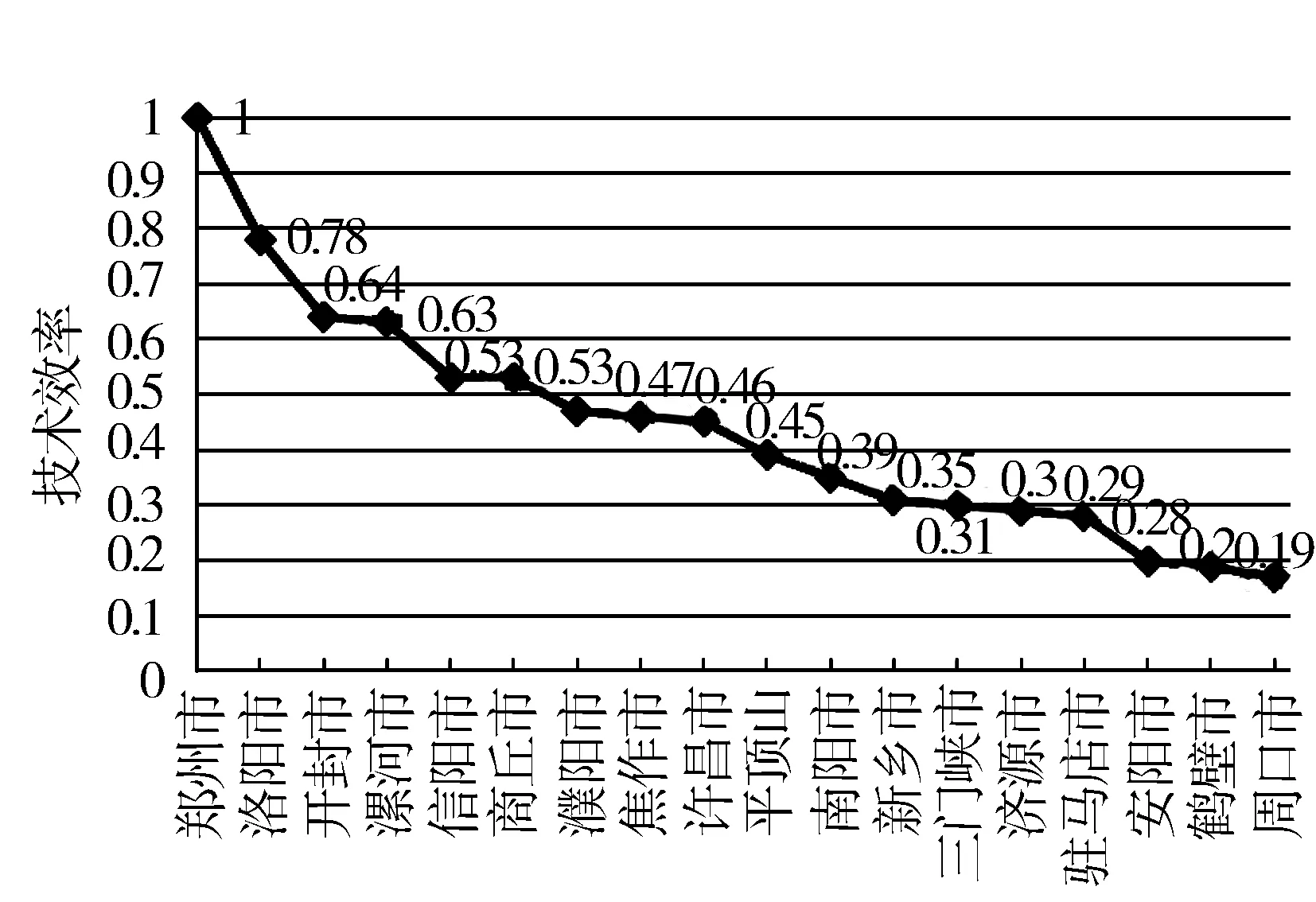
图2 第三阶段各城市技术效率
以郑州为中心的城市群:洛阳市技术效率为0.78、焦作市技术效率为0.46、新乡市技术效率为0.31、开封市技术效率为0.64、许昌市技术效率为0.45,可以发现只有洛阳的技术效率超过0.7,其他城市的技术效率均较低,说明省会郑州的辐射能力不强。除了郑州附近的城市群,其他城市无论东南部城市还是西北部城市技术效率均更低。总体上,河南各城市技术效率呈现以郑州为中心的中部城市技术效率偏高,其他城市较低。河南十八个地市的科技效率,郑州最好为1,其他地市最好的仅为0.78,最差的才0.17,也就是说其他城市与郑州市的科技效率差距较大。从十八个地市所处的位置来看,郑州市是河南的经济、文化、政治中心,所以各方面的资源优势比较强,科技效率最好;科技效率较低的地市都是处在河南省的边远地区或者山区,这些地区的资源优势相对较弱。
(3)城市效率的演进特征。图3显示2007年到2012年河南城市技术效率值,2009年最大为0.48,2010年最小为0.4,差别不大,六年来河南城市技术效率均在0.5的水平上徘徊,没有明显改善的趋势,说明河南城市总体上技术效率有待改善。河南是农业大省,工业基础相对东部地区较薄弱,辖区内的科研机构、高等院校也相对较少,造成河南城市科技效率都相对较低,但随着中原经济区、郑州航空港综合实验区等国家规划的确立,加上新一届政府提出的城镇化政策,河南城市科技效率有望逐步提高。
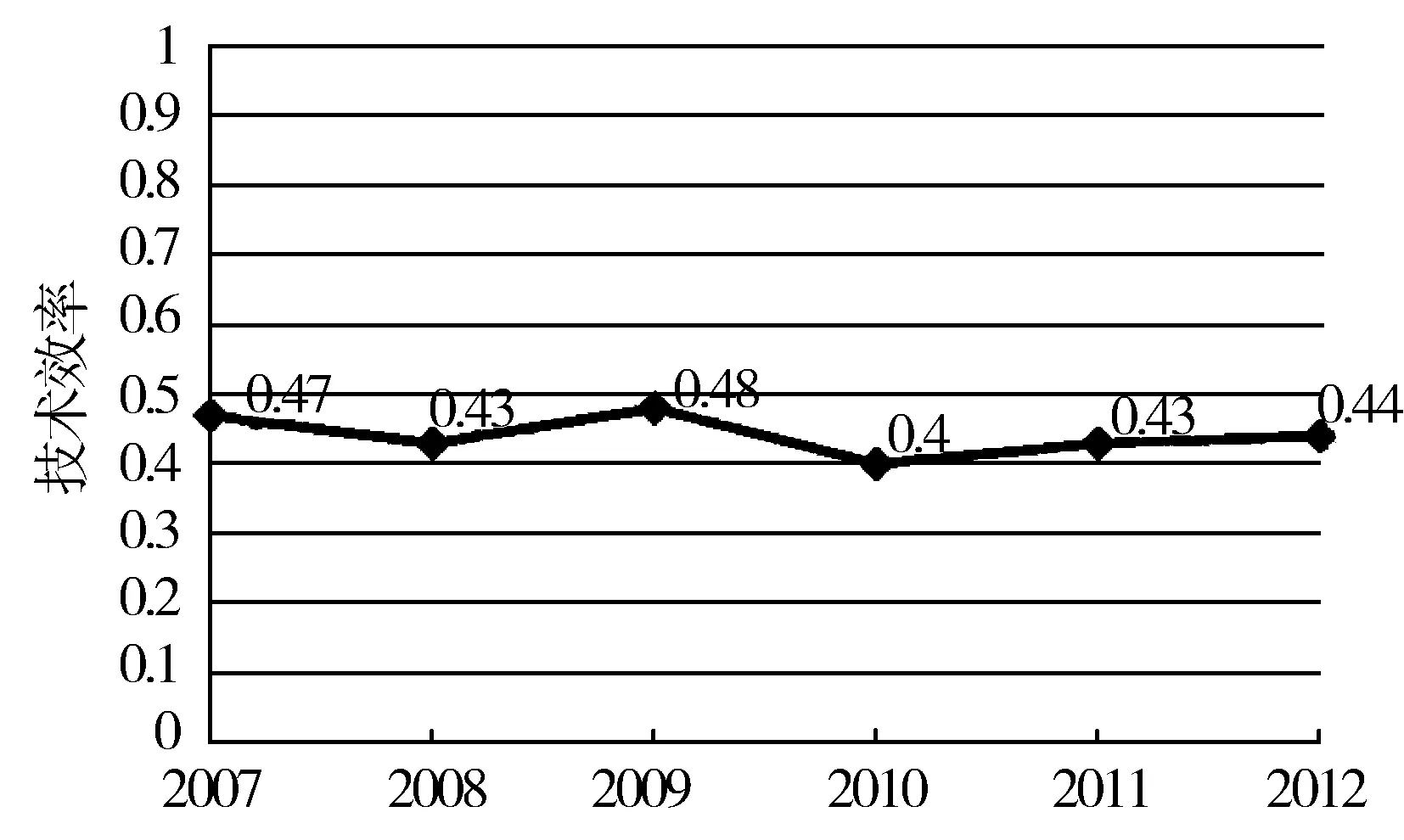
图3 第三阶段不同年份技术效率
(4)大部分城市投入产出还存在较大改善空间。如表4所示,18个城市中有11个城市技术效率小于0.5,特别是鹤壁市和周口市技术效率竟然分别为0.19和0.17,大部分城市三项效率得分均处于较低水平,表明其不但面临投入不足,而且科技资源的使用效率也处于较低的态势,说明这些城市技术效率有很大改善空间。这些效率较低的地市都是处在边远地区或山区,如周口市是传统的农业大市,在河南新一届政府提出直管县等体制改革后,加上国家战略对中原地区的倾斜,科技效率相对落后的河南城市定能迎来春天。

表4 技术效率小于0.5的城市
(5)第三阶段规模报酬分析。规模报酬变化指的是在其他条件不变的前提下,企业内部各生产要素按相同比例变化时而带来的产量变化。企业规模报酬变化可分为规模报酬不变、规模报酬递增以及规模报酬递减三种情况。如果企业所有投入增加一倍,产出相应也增加一倍,则称之为规模报酬不变;如果企业所有投入增加一倍,而产出增加超过一倍,则存在递增的规模报酬;如果所有投入增加一倍,而产出增加小于一倍,则称之为规模报酬递减。大规模的生产使劳动的分工更为专业化,能充分利用先进的设备和大规模的厂房,这种情况下很可能会产生规模报酬递增;而当企业规模过于庞大和组织的复杂性带来了管理上的困难,从而降低了劳动和资本的生产率,这种情形下则可能出现规模报酬递减。
整个河南省城市从2006年到2012年中,除了九个样本属于DEA有效外,其他样本均处于规模效率递增,即等比例地增加一倍投入,产出的增加会超过一倍。这说明河南省各城市总体上科技机构规模偏小,可进一步扩大规模以提高科技机构的综合技术效率。
4.第一阶段和第三阶段效率比较分析
首先针对第一阶段和第三阶段效率值做相关性分析与差异性检验,再比较分析两个阶段效率的差异。
(1)相关性分析与差异性检验。根据第一阶段和第三阶段各个效率值做相关性分析,并使用配对样本T检验考察两者之间是否有显著的差异性。

表5 第一阶段和第三阶段效率相关性
表5是配对样本的描述性统计结果,从中可以看出,第一阶段和第三阶段技术效率均值分别为0.4696和 0.4431,差异不大。纯技术效率均值0.5214 (第一阶段) 明显低于0.9872 (第三阶段)。而规模效率均值0.8794 (第一阶段)却高于0.4477 (第三阶段)。第一阶段和第三阶段的技术效率、纯技术效率和规模效率的相关系数分别为0.848、0.597 和 0.356,而且线性相关的统计性显著。说明两种方法计算出来的效率值之间具有相关性,技术效率的相关性最强,规模效率的相关性相对较弱。

表6 成对样本T检验
表6配对样本T 检验的结果显示,第一阶段技术效率和第三阶段技术效率的配对差的均值为 0. 0266,标准差为 0. 1616,平均标准误差为 0. 0156,95%的置信区间为(-0. 0043,0. 0574),t统计量值为 1.71,自由度为 107,t检验的双尾显著性概率为 0.09>0.05,说明第一阶段和第三阶段的技术效率值差异不显著。同理,第一阶段纯技术效率和第三阶段纯技术效率的t检验的双尾显著性概率0.000<<0.05,说明第一阶段和第三阶段的纯技术效率之间有显著的差异;第一阶段规模效率和第三阶段规模效率的t检验的双尾显著性概率0.000<<0.05,即第一阶段和第三阶段的规模效率之间差异显著。
综上,通过对第一阶段和第三阶段测度的效率值进行T检验,第一阶段和第三阶段的技术效率之间差异不显著,第一阶段和第三阶段的纯技术效率、第一阶段和第三阶段的规模效率两对差异显著。说明环境变量的存在和随机误差干扰的影响,导致第一阶段和第三阶段效率值之间的差异存在。技术效率差异不显著,是因为纯技术效率提高的程度和规模效率降低的程度相差不大,所以最终导致技术效率的变化不显著。
(2)比较分析第一阶段和第三阶段效率的差异。比较第一阶段和第三阶段效率值,得出如下结果。
首先,环境因素调整后效率得分差异度总体下降。第一阶段和第三阶段的技术效率方差分别为0.30507和0.26043,呈现下降趋势;第一阶段和第三阶段的纯技术效率方差分别为0.30732和0.01162,呈现下降趋势;第一阶段和第三阶段的规模效率方差分别为0.15538和0.26001,呈现上升趋势。出现这种情况的原因,可以认为调整前环境好的城市,较好的环境条件能上扬技术效率得分,环境较为恶劣的地区则压低技术效率得分,因而造成技术效率得分差异度较大,调整后使所有城市均处于相同的环境下,排除随机误差的影响,效率得分的差异度明显缩小。因此,调整后的结果更能客观反映河南省各城市的真实效率情况,三阶段DEA效率得分对河南省各城市科技效率解释的准确性和可信性增强。
其次,环境因素调整后效率得分变化。第一阶段和第三阶段的技术效率均值分别为0.4696和0.4431,略有下降;第一阶段和第三阶段的纯技术效率均值分别为0.5214和0.9872,大幅增大;第一阶段和第三阶段的规模效率均值分别为0.8794和0.4477,大幅降低。具体来看,调整前后的效率值以及规模报酬情况出现较大幅度的变化,说明河南城市技术效率受环境变量的影响较为显著,环境变量对效率值的影响方向是不确定的,控制外生变量与随机误差的影响后,技术效率变化不大,但纯技术效率大幅增大,而规模效率大幅降低。调整后的数据分析,在维持现有产出水平不变的条件下,投入减少53.04%可以达到有效生产前沿面,技术效率分解来看,必须减少1.28%的投入达到纯技术效率有效,调整要素投入结构,减少55.23%的投入达到规模有效。
最后,环境因素调整前后城市技术效率均值变化。按照调整后效率变化值降序排序绘制表7,其给出了调整前和调整后的各城市技术效率平均值的变化数据,可以看出,调整前与调整后部分城市效率值存在较大变化,这意味着如果不考虑外界环境条件和随机误差的影响,得出的效率评价值可能存在某种程度的偏差。调整前技术效率大于等于0.75的城市有郑州市、漯河市、洛阳市、鹤壁市和济源市;调整后技术效率大于等于0.75的城市有郑州市和洛阳市。调整前后效率变化最大的前两个城市是济源市和漯河市,说明环境因素对其影响较大。

表7 调整前后城市技术效率均值变化
三、结 论
从以上的实证分析中,可以得出以下结论。
(1)第一阶段与第三阶段的效率值存在明显差异,这说明各城市环境因素确实对它们的科技效率产生了重大影响。同时,剔除环境因素的DEA三阶段模型测度出来的效率值更能反映科技效率。
(2)总体上,河南各城市技术效率呈现以郑州为中心的中部城市技术效率偏高,其他城市较低;其他城市与郑州市的科技效率差距较大。
(3)2007年到2012年间,河南各城市技术效率均值改善不明显,说明河南城市总体上技术效率有待改善。
(4)样本期间,河南省城市技术无效的主要因素来自于规模效率,说明河南各城市改革的重点在于如何更好地发挥其规模效益。
(5)大部分城市三项效率得分均处于较低水平,表明其不但面临投入不足,而且科技资源的使用效率也处于较低的态势,说明大部分城市投入产出还存在较大改善空间。
参考文献:
[1]Banker R D,Charnes A,Cooper W W. Some models for estimating technical and scale inefficiencies in date envelopment analysis [J]. Management science, 1984, 30(9):1078-1092.
[2]Cooper W W, Seiford L M and Tone K. Data envelopment analysis: A comprehensive text with models [M]. Applications, references and DEA-solver, Kluwer academic publishers, Boston. 2000.
[3]Zhong W, Yuan W, Li S X, et al. The performance evaluation of regional R&D investments in China: An application of DEA based on the first official China economic census data [J]. Omega, 2010,(39):447-455.
[4]Banker R D, Natarajan R. Evaluating contextual variables affecting productivity using data envelopment analysis[J]. Operations Research, 2008,(56):48-58.
[5]Zhu J. Data envelopment analysis to evaluate efficiency in the economic performance of Chinese cities[J].socio-economic planning science, 1989,(23):325-344.
[6]Ruggiero J.A comparison of DEA and the stochastic frontier model using panel data [J].International Transactions in Operational Research,2007,(14):259-266.
[7]FRIED H O. Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis[J], Journal of Productivity Analysis,2002,(17):157-174.
[8]黄 森,蒲勇健.中国省域经济综合效率分析——基于三阶段DEA模型的研究[J].山西财经大学学报,2010,(3):23-29.
[9]邵 军,徐康宁.我国城市的生产率增长、效率改进与技术进步[J].数量经济技术经济研究,2010,(1):58-67.
[10]戴永安.中国城市效率差异及其影响因素——基于地级及以上城市面板数据的研究[J].上海经济研究,2010,(12):12-19.
[11]刘和东.中国区域研发效率及其影响因素研究——基于随机前沿函数的实证分析[J]. 科学学研究,2011,29(4):548-556.
[12]黄 宪,余 丹,杨 柳.我国商业银行X效率研究——基于 DEA 三阶段模型的实证分析[J].数量经济技术经济研究,2008,(7):80-91.
[13]贺京同,冯 尧.中国高技术产业科技成果转化效率的实证研究——基于 DEA - Malmquist 指数方法[J].云南社会科学,2011,(4):92-97.
