地下洞室开挖围岩弹塑性动态稳定性分析

曾新发 ，彭振斌，何杰，李运成，彭凯

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；2. 湖南城市学院 城市管理学院，湖南 益阳，413002；3. 湖南工业大学 土木工程学院；湖南 株洲，412007；4. 中国水电顾问集团 中南勘测设计研究院，湖南 长沙，410014)

材料的屈服准则选择合理与否对强度储备安全系数的计算精度有很大的影响[1-4]。目前，对于岩土体这一类摩擦型弹塑性材料，在数值计算中屈服准则常采用 Mohr-Coulomb(M-C)准则和 Drucker-Prager(D-P)准则。(M-C)准则能较好地反映岩土材料拉压特性，但是在三维应力空间中屈服面存在奇异点导致数值计算不收敛，为此前人对此作了大量的修正，主要对π平面上六角形进行了修圆处理[5-8]，较好地解决了M-C准则棱角处不收敛的问题，但公式过于复杂不便于应用。不同于M-C，Drucker-Prager (D-P)准则在π 平面上是M-C 准则的内切圆，表述简单且易于数值计算。D-P 类准则主要包括M-C 外角外接圆、内角外接圆、摩尔库仑等效面积圆[9]、摩尔匹配圆等。不同的D-P准则计算得到的塑性区大小是不同的[10]。在三维应力空间中，Mohr-Coulomb 内切圆锥屈服准则下强度储备安全系数最小，Mohr-Coulomb 外接圆锥屈服准则下强度储备安全系数最大。这表明，强度储备安全系数的大小与屈服准则之间存在某种函数关系。地下洞室在开挖过程中，由于应力释放而引起主应力差的变化，对洞室围岩应力及变形产生不利影响，进而可能会导致洞室围岩失稳[11-15]。当然，施工开挖方式、支护方式的选择对围岩应力、位移及安全系数有着重要影响，不同的开挖和支护方式将获得不同的围岩稳定效果[16-22]。本文作者从理论上分析了强度储备安全系数与经典Drucker-Prager 屈服准则的函数关系，研究了主应力的变化对安全强度储备系数的影响。结合糯扎渡水电站调压井复杂洞室群特点，对其开挖施工过程中围岩的应力、变形及关键点安全系数进行了计算分析，系统评价了该调压井洞室群因开挖造成的稳定性问题。针对开挖过程中，局部点安全系数偏小的情况，通过3 个混凝土二次衬砌方案的比选，得出最优支护方案，为水电站大型地下洞室开挖及支护问题的解决提供借鉴。

1 D-P 屈服准则安全系数的表达式

在三维应力空间中D-P 准则可写为：

式中：I1和J2分别为应力张力第一不变量和应力偏量第二不变量； aφ和k 为材料参数，其中

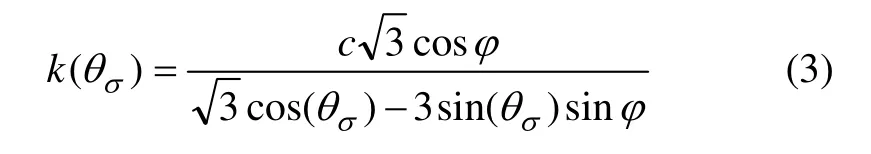
式中：θσ为应力罗德角；c 和φ 分别为黏聚力和内摩擦角。

由式(1)可以看出：罗德角取不同的值便可以得到不同的 aφ和k。因此，安全系数与Drucker-Prager 屈服准则的关系可以归结为安全系数与罗德角θσ的关系。

按照强度储备法的定义，有限元强度折减法[22]是将岩土材料参数c 和φ 同时除以一折减系数Kc，得到一组新的c′和φ′，再作为新参数输入进行计算，当计算正好收敛时(此时边坡处于极限平衡状态)所得到的Kc即为边坡稳定安全系数。计算中仅对材料的黏聚力c 和内摩擦角φ 的正切值做折减，如下式所示：

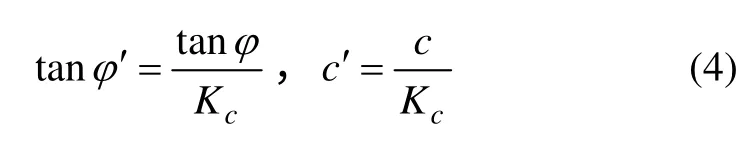
将式(4)代入式(1)，整理得：

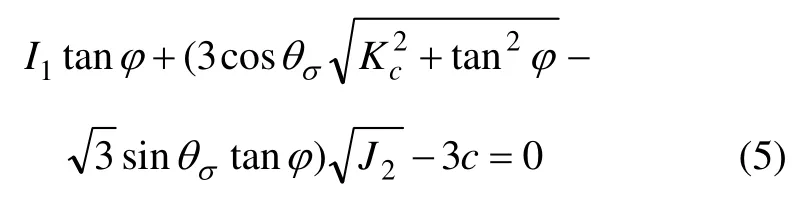
将式(5)写成Kc表示的θσ的函数为：

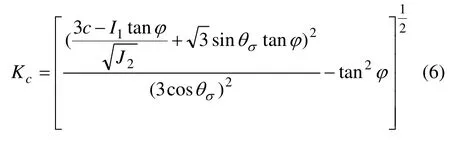
对于理想弹塑性材料而言，屈服就意味着破坏，因此，此时屈服准则也就是破坏准则，故式(6)即为点安全储备系数系数与Drucker-Prager 屈服准则的关系。

由式(5)可知：屈服准则F 可以看成是Kc及θσ的函数，对其分别求导可得：

由式(7)和(8)可以得到Kc关于θσ的一阶导数：

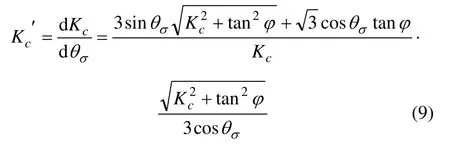
令式(9)等于零有：

由式(9)进一步有：

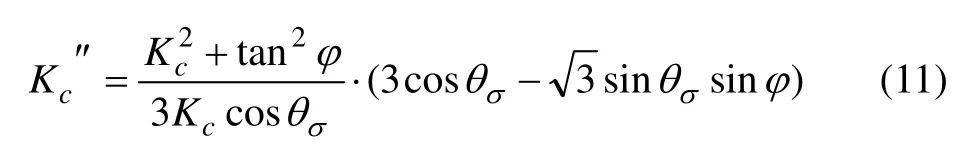
由式(10)及θσ∈[-π/6,π/6]有：

由 式(9)～(11) 可 知： 当θσ∈[-π/6,θσ*]，K′(θσ)＞0，K′ (θσ)＜0，K(θσ)单 调 递 减；当θσ∈[θσ*,π/6]时，K′ (θσ)＞0，K′ (θσ)＞0，K(θσ)单调递增。

对于地下深长洞室，可以视为平面应变问题，假定式(6)中，c=0.45 MPa，φ=33°，μ=0.30，取3 组不同的σ1和σ3进行对比分析，分别取K1=K(-π/6)，K2=K(θσ*)，K3=K(π/6)计算结果如表1 和图1所示。

从表1 和图1 可以看出：随着主应力差的不断增大， 材料的储备安全系数不断减小。 当θσ∈[-π/6,θσ*]，主应力差越大，Kc(θσ)减幅越大，但Kc(θσ)整体趋势变化不大；θσ∈[θσ*,π/6]时，Kc(θσ)增幅较明显。

以上分析表明：当材料强度不变时，随着主应力差的变化，材料可能由安全变得不安全，甚至破坏。在隧道、地下厂房等地下洞室的开挖施工过程中，由于应力释放，导致主应力差组合不断的发生变化，进而可能引起洞室围岩失稳破坏。

图1 不同应力罗德角θσ 与安全储备常数Kc 的关系Fig.1 Relationship between different stress Rhodes angle θσ and reserves of safety factor Kc

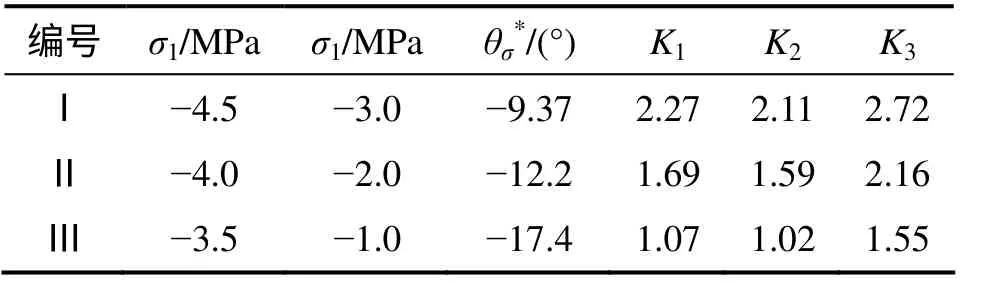
表1 不同σ1 和σ3 时的计算结果Table 1 Calculating results at different σ1 and σ3

2 屈服准则的有限元数值分析

基于上述Drucker-Prager 屈服准则与材料安全系数的关系，采用有限元强度折减法，结合糯扎渡水电站调压井大型地下洞室群开挖和支护工程，通过三维有限元数值计算，分析了开挖过程中，围岩稳定安全系数随开挖步的动态变化关系，基于局部区域关键点安全系数偏小的情况，通过支护方案比选，得到了该工程最经济合理支护方案。

2.1 工程概况及三维模型

糯扎渡水电站尾水建筑物包括尾水支洞、尾水闸门室、尾水调压井、尾水隧洞、出口检修闸门室和尾水渠，按三机一调一尾格局布置，共布置9 条尾水支洞、3 个调压井和3 条尾水隧洞。3 个调压井按“一”字形布置，间距为102 m，中心连线方位角为NE76°。计算考虑洞室有3 个调压井、连通上室、9 条尾水支洞、3 条尾水隧洞，地质构造包括Ⅲ级断层F20，F21和F22。地质剖面示意图如图2 所示。1 号调压井开挖直径为29.3～34.3 m，2 号和3 号调压井开挖直径为31.3～34.3 m。调压井下部为五洞交叉口结构，即3 条尾水支洞汇入1 个调压井，每个调压井接1 条尾水隧洞。

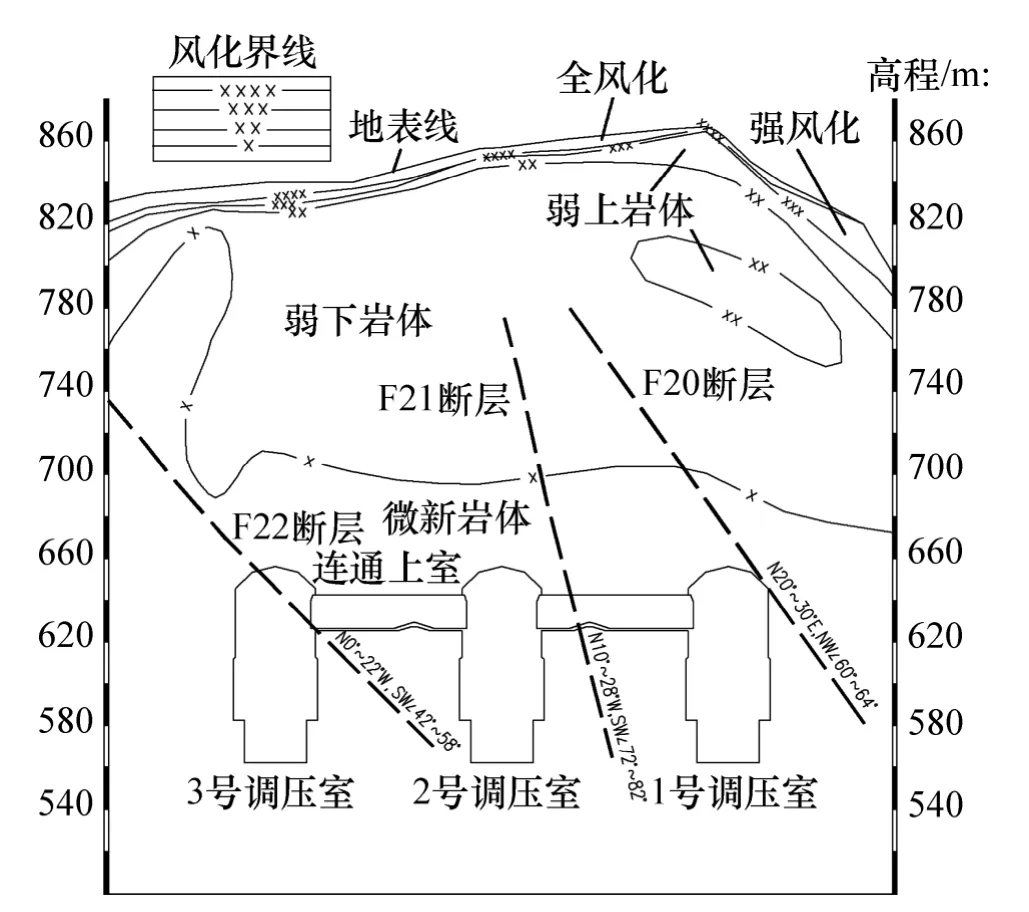
图2 调压井工程区地质剖面示意图Fig.2 Diagrammatic sketch of geologic section for surge shaft project area

三维计算模型范围：X 坐标范围为-349～-103 m，Y 坐标范围为0～450 m，Z 坐标范围为501～865 m，共划分单元184 336 个，节点38 954 个，采用位移边界，实体单元模拟，地下洞室布置及断层位置示意图见图3。洞室总共分38 步开挖，尾水支洞和尾水隧洞均分三层开挖，根据设计顺序错动开挖，调压井井身及五洞叉口开挖步骤示意图见图4，开挖顺序为：A1，A2，…， A7，C1，B1，B2，…，B15，C2，C3，C4。各岩层围岩计算参数见表2。

2.2 施工期开挖成果分析

选取典型断面，断面剖切位置坐标x=-225.97 m，对调压井洞室在开挖过程中围岩动态稳定性进行研究。典型断面上，各个关键点位置如图5 所示。各关键点总位移、小主应力(拉正压负)、安全系数随开挖步的动态变化曲线见图6～8。

由图6 可知：关键点总位移随开挖步的递进而持续增加，开挖初期，调压井上部关键点位移增长较快，且有小幅波动。中部关键点位移初期增长较慢，当开挖进行到一半左右，亦即当开挖高程达到该关键点处时，位移迅速增长，随后位移仍有所增长，但是总体而言趋于平缓。下部关键点在开挖后期增长较快，开挖过程中，最大位移位于调压井下部关键点下1 处，达10.57 mm。

由图7 可以看出：当开挖高程达到该关键点所处的高程时，小主应力突然变大，呈现出阶梯状跳跃式变化，局部区域出现拉应力，其位置与最大位移发生的位置一样，也位于调压井下部，在关键点下3 处，最大拉应力1.10 MPa。当开挖高程尚未达到该关键点高程或者业已超过该点高程时，小主应力随开挖进行变化趋于平缓。

图8 表明：关键点安全系数(Fs)随开挖步的进行而不断降低，当开挖高程达到该关键点所处的高程时，该点的安全系数呈现出断崖式下降，这一点与小主应力的变化规律正好相反，但是其两者发生突变的进程却基本吻合。

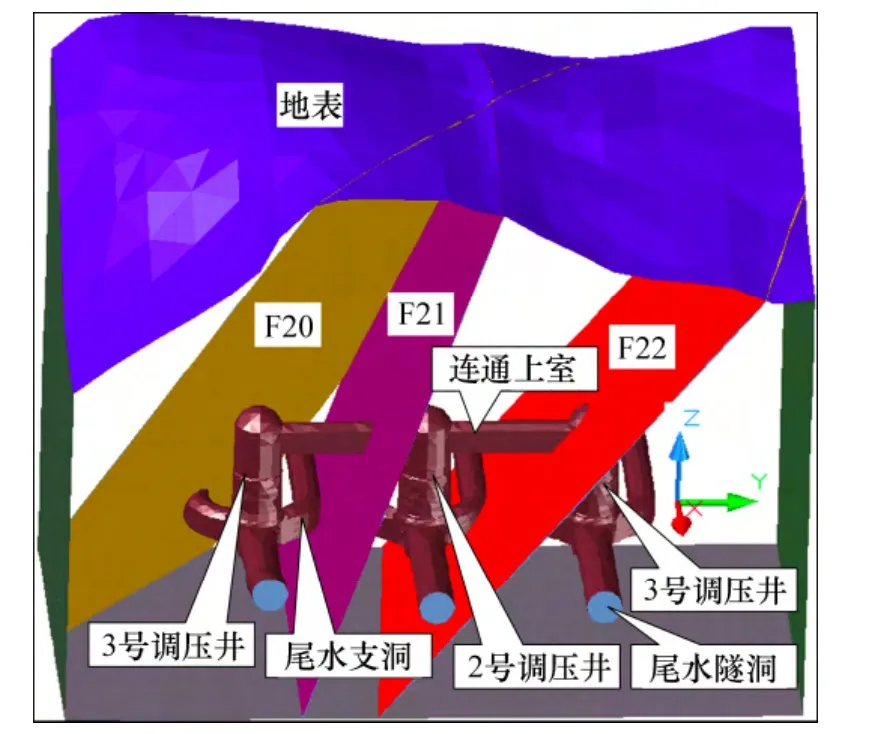
图3 地下洞室布置及断层位置示意图Fig.3 Diagrammatic sketch of underground cavern layout and fault position

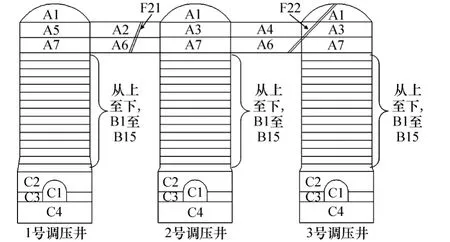
图4 洞室开挖步骤示意图Fig.4 Diagrammatic sketch of excavation steps of cavern

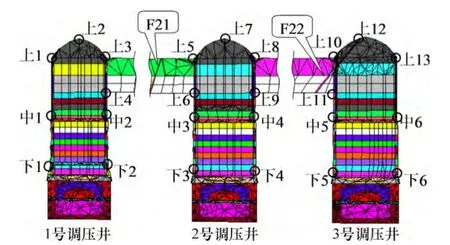
图5 典型断面x=-225.97 m 上关键点位置示意图Fig.5 Diagrammatic sketch of key points position at typical section with x=-225.97 m

表2 弹塑性数值计算围岩力学参数Table 2 Mechanical parameters of rock mass for elastic-plastic numerical calculation

图6 关键点总位移随开挖进行的动态变化曲线Fig.6 Dynamical change curve of total displacement of key points with excavation of cavern

图7 关键点小主应力随开挖进行的动态变化曲线Fig.7 Dynamical change curve of minimum principal stress of key points with excavation of cavern

此外，调压井上部关键点安全系数在开挖初期降幅最大，而中部关键点安全系数最小值发生在开挖中期，约开挖总步的一半左右；开挖后期，下部关键点的安全系数取得最小值，这表明，随着开挖的不断进行，洞室围岩的失稳过程是由顶部向底部不断扩展。根据DL 5180—2003(《水电枢纽工程等级划分及设计安全标准》)和SL 266—2001《(水电站厂房设计规范》)，对于岩基基础类别，调压井施工期最小安全系数要求为1.05。施工期围岩安全系数不满足规范要求的关键点统计见表3。

从表3 可以发现：洞室拐角点和断层切割点附近安全系数相对较小，当洞室开挖至某关键点而导致该点围岩突然卸荷时，该点位移和小主应力表现为骤升，点安全系数表现为骤降，而之前保持较小速率或恒速变化，三者变化时刻基本相同，说明洞室开挖造成的主应力差的变化对围岩稳定极为不利。

图8 关键点安全系数随开挖进行的动态变化曲线Fig.8 Dynamical change curve of safety factor of key points with excavation of cavern

当然，局部区域个别点安全系数偏小，并不就代表整个洞室围岩稳定就不安全。为进一步研究洞室围岩的整体稳定性，选取洞室全部开挖后X=-225.97 m断面安全系数云图进行分析，见图9。

由图9 可见：洞室拐角点及断层与洞室相交点安全系数较低，与前述分析一致，围岩最小安全系数为1.10 左右，满足规范要求。对比关键点安全系数曲线，说明调压井围岩中只有个别点安全系数不满足规范要求，围岩整体稳定性较好，开挖主要造成围岩局部表面破碎，不会形成大面积破坏。

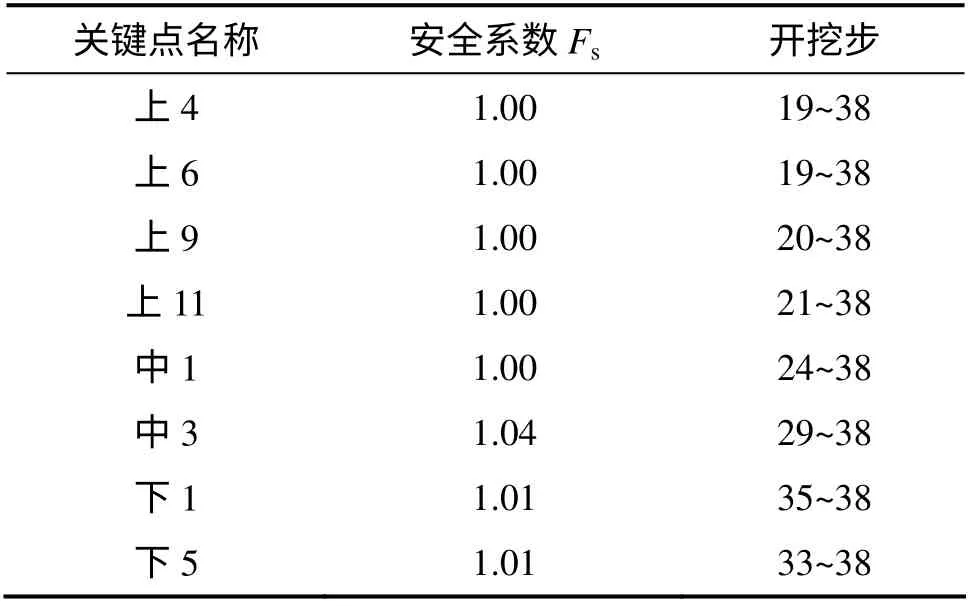
表3 安全系数小于规范要求的关键点Table 3 Key point of which safety factor is less than standard

图9 施工期断面安全系数云图Fig.9 Safety factor nephogram of typical section in construction period

3 二次衬砌后稳定性分析

针对上述个别关键点安全系数不满足规范要求的情况，必须对调压井实施二次衬砌支护。二次支护衬砌主要支护参数见表4，混凝土采用弹性材料模拟，力学参数见表5。

为确定既经济又能满足围岩稳定要求的混凝土浇筑高程，预选混凝土衬砌分别浇筑至高程583.3，613.5和625.50 m 3 个方案进行模拟对比计算，调压井二次衬砌示意图见图10。

经二次衬砌后，典型断面上各关键点安全系数的变化见图11。由图11 可知：当二次衬砌高程低于关键点所处高程，该关键点安全系数基本不变；当二次衬砌高程大于关键点所处高程，该关键点安全系数增大明显，且均大于1.05，满足规范关于洞室围岩的相关稳定要求。

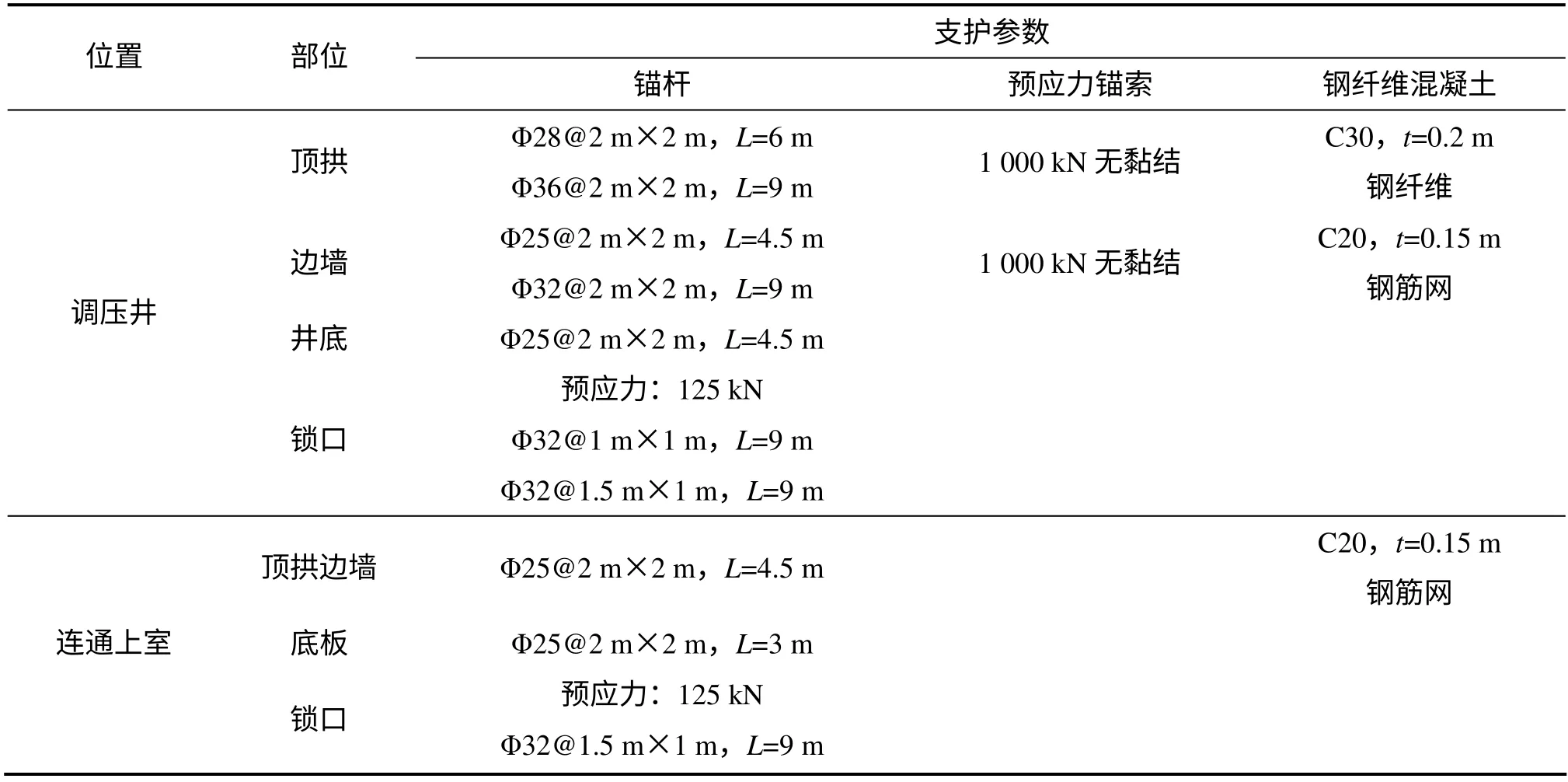
表4 调压井工程区支护参数Table 4 Support parameters of surge shaft project area

表5 混凝土二次衬砌力学参数Table 5 Mechanical parameters of concrete lining for secondtime

图10 调压井二次衬砌示意图Fig.10 Diagrammatic sketch of lining for second time of surge shaft

关键点1 中安全系数变化最小，当混凝土浇筑至625.5 m 时，安全系数才达到1.07。通过上述几个方案数值计算和比选，调压井混凝土浇筑至625.5 m 高程方能完全满足围岩稳定要求，因此，这一方案是最安全也是最经济合理的方案。

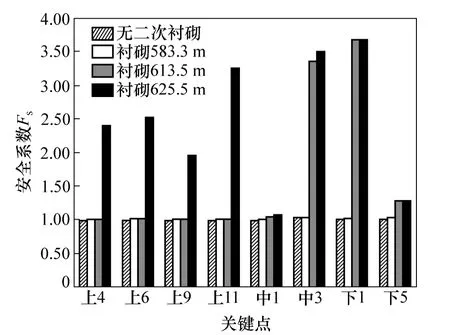
图11 随衬砌高程变化的安全系数直方图Fig.11 Histogram of safety factor with elevation changes of lining

4 结论

(1) 推导了Drucker-Prager 准则安全系数的表达式，分析了主应力差的变化对安全系数的影响。

(2) 采用D-P 准则，对糯扎渡水电站大型地下洞室群开挖施工造成的围岩稳定性问题进行模拟分析，结果表明，当洞室开挖至某关键点而导致该点围岩突然卸荷时，该点位移和小主应力表现为骤升，点安全系数表现为骤降，说明洞室开挖造成的主应力差突变对围岩稳定极为不利。

(3) 洞室开挖后，关键点总位移、小主应力随开挖的进行而持续增加，点安全系数随开挖的递进而逐渐减小。最大位移以及最大拉应力均发生在调压井下部，分别为达10.57 mm 和1.1 MPa。随着开挖的不断进行，洞室围岩潜在的失稳过程是由顶部向底部不断扩展。

(4) 开挖过程中，围岩整体稳定，但少数关键点安全系数小于规范规定要求，主要发生在洞室拐角点和断层切割部位。

(5) 当二次衬砌高程大于关键点所处高程时，该关键点安全系数增大明显，且均大于1.05，满足规范稳定要求。通过方案比选，当调压井混凝土浇筑至625.5 m 高程时，能完全满足围岩稳定要求，也是最经济合理的方案。

[1] Matsui T, SAN Kaching. Finite element slope stability analysis by shear strength reduction technique[J]. Soils and Foundations,1992, 32(1): 59-70.

[2] 郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381-3388.ZHENG Yingren, ZHAO Shaoyi. Application of strength reduction FEM in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388.

[3] Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387-403.

[4] 郑颖人, 赵尚毅, 时卫民, 等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 2002, 24(3): 343-346.ZHENG Yingren, ZHAO Shaoyi, SHI Weimin, et al. Analysis of safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343-346.

[5] Koiter W T. Stress-strain relations, uniqueness and variational theorems for elasto-plastic materials with a singular yield surface[J]. Quarterly of Applied Mathematics, 1953, 11:350-354.

[6] Chen W F. Limit analysis and soil plasticity[M]. Amsterdam:Elsevier Scientific Press, 1975: 637-639.

[7] Lade P V, Nelson R B. Incrementalization procedure for elasto-plastic constitutive model with multiple, intersecting yield surfaces[J]. International Journal for Numerical and analytical methods in Geomechanics, 1984, 8(4): 311-323.

[8] Gudehus G. A comprehensive constitutive equation for granular materials[J]. Soils and Foundations, 1996, 36(1):1-12.

[9] 徐干成, 郑颖人. 岩土工程中屈服准则应用的研究[J]. 岩土工程学报, 1990, 12(2): 93-99.XU Gancheng, ZHENG Yingren. Study on application of yield criterions in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(2): 93-99.

[10] 张鲁渝, 时卫民, 郑颖人. 平面应变条件下土坡稳定有限元分析[J]. 岩土工程学报, 2002, 24(4): 487-490.ZHANG Luyu, SHI Weimin, ZHENG Yingren. The slope stability analysis by FEM under the plane strain condition[J].Chinese Journal of Geotechnical Engineering, 2002, 24(4):487-490.

[11] 王海军, 任旭华, 张继勋. 大型长廊式调压室围岩稳定性数值仿真分析[J]. 三峡大学学报(自然科学版), 2009, 31(1):26-29.WANG Haijun, REN Xuhua, ZHANG Jixun. Numerical simulation analysis of stability of wall rock of large long corridor surge chamber[J]. Journal of China Three Gorges University(Natural Sciences), 2009, 31(1): 26-29.

[12] 苏向震, 何江达. 调压室开挖与支护的数值模拟分析[J]. 四川水利, 2006(4): 61-65.SU Xiangzhen, HE Jiangda. Numerical simulation analysis of excavation and support in surge chamber[J]. Sichuan Water Conservancy, 2006(4): 61-65.

[13] 刘国伟, 熊峰. 调压井施工开挖过程稳定性仿真分析[J]. 地下空间与工程学报, 2005, 1(2): 305-309.LIU Guowei, XIONG Feng. Simulated process analysis for the excavating construction of surge-shaft[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(2): 305-309.

[14] 肖明. 地下洞室施工开挖三维动态过程数值模拟分析[J]. 岩土工程学报, 2000, 22(4): 421-425.XIAO Ming. Three-dimensional numerical model of construction process for underground opening[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(4): 421-425.

[15] 刘进宝, 李守巨, 刘迎曦. 水电站地下厂房岩锚吊车梁结构参数数值分析[J]. 中国农村水利水电, 2006(3): 37-42.LIU Jinbao, LI Shouchen, LIU Yingxi. Numerical analysis of structural parameters for rock anchor hoist beam in underground workshop of hydropower station[J]. China Rural Water and Hydropower, 2006(3): 37-42.

[16] 袁金亮, 肖明, 傅志浩. 陡倾角岩体中阻抗式圆形调压井衬砌结构数值分析[J].岩石力学与工程学报, 2004, 23(8):1296-1300.YUAN Jinliang, XIAO Ming, FU Zhihao, FENG Xia-ting.Numerical analysis on lining structure of restricted cylindrical surge chamber in rock masses with steep obliquity[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8):1296-1300.

[17] 茹忠亮, 冯夏庭, 李洪东, 等. 大型地下工程三维弹塑性并行有限元分析[J]. 岩石力学与工程学报, 2006, 25(6): 1141-1146.RU Zhongliang, FENG Xiating, LI Hongdong, et al. 3D elastoplastic parallel finite element analysis of large-scale underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1141-1146.

[18] 冯夏庭, 刁心宏. 智能岩石力学—导论[J]. 岩石力学与工程学报, 1999, 18(2): 222-226.FENG Xiating, DIAO Xinhong. Intelligent rock mechanics introduction[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(2): 222-226.

[19] 钱向东, 焦彩虹. 基于多参数强度准则的安全系数定义问题[J]. 水利水电科技进展, 2007, 27(4): 34-37.QIAN Xiangdong, JIAO Ciahong. On definitions of safety factor based on multi-parameter strength criterion[J]. Advances in Science and Technology of Water Resources, 2007, 27(4):34-37.

[20] 聂卫平, 徐卫亚, 周先齐. 基于三维弹塑性有限元的洞室稳定性参数敏感性灰关联分析[J].岩石力学与工程学报, 2009,28(增2): 3885-3893.NIE Weiping, XU Weiya, ZHOU Xianqi. Grey relation analysis of parameter sensitivity of cavern stability based on 3D elastoplastic finite elements[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl.2): 3885-3893.

[21] 叶超, 肖明, 杨亚玲. 地震作用下大型多岔调压井衬砌结构数值分析[J]. 岩土力学, 2008, 29(增1): 21-25.YE Chao, XIAO Ming, YANG Yaling. Numerical analysis of large multifork surge-shaft lining structure under seismic action[J]. Rock and Soil Mechanics, 2008, 29(Suppl.1): 21-25.

[22] 张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 2003(1): 21-27.ZHANG Luyu, ZHENG Yingren, ZHAO Shangyi, et al. The feasibility study of strength reduction method with FEM for calculating safety factors of soil slope stability[J]. Journal of Hydraulic Engineering, 2003(1): 21-27.