XFAST 长码直捕算法参数优化设计
2014-04-01唐小妹庞晶黄仰博王飞雪
唐小妹,庞晶,黄仰博,王飞雪
(国防科学技术大学 电子科学与工程学院 卫星导航研发中心,湖南 长沙,410073)
GPS 信号采用C 码和P 码2 种不同的伪随机码。其中,C 码是一种低码率、周期重复的短码,主要用于民用系统;P 码也称为军码,是一种高码率、长周期、加密伪随机码[1]。在正常情况下,可以通过对C码信号的捕获跟踪,实现对P 码信号的引导;在战争或者某种突发事件的情况下,C 码信号可能会被干扰或者关闭,这就要求军用导航接收机具有长码直接捕获的功能。由于接收机的晶振漂移和信号的传播时延未知等因素,使得本地伪码相位与接收信号的伪码相位之间存在一定的不确定度(图1 中的Δt),在实际应用中该不确定度最大为秒级,P 码码率为10.23 Mcps,即要求快速搜索107量级的码片数;同时,由于用户相对于卫星运动和接收机晶振的频差,导致接收到的信号相对于标称频率有一定的频率偏差(图1 中的Δf,一般频率不确定范围为+/-6 kHz)。故长码直捕过程是一个时域和频域的二维搜索过程,具体如图1 所示,对每个分格(δf 和δt)进行相关值计算,相关值最大且过门限的点即为待捕获的信号。目前的长码直捕算法[1-2]可以分为以下3 类:(1) 时域捕获[1],通过时域的匹配滤波器的实现方式对伪码相关值的计算,该方法对硬件资源需求大,且平均捕获时间较长;(2) 频域捕获[3-5],利用频域相乘等效于时域卷积的思想进行相关值的计算,可同时进行多普勒频偏和伪码相位的搜索;(3) 时频结合[6],对时域相关后的结果进行频率的估计,在搜索码相位的同时进行频偏估计,提高捕获速度。由Yang 等于2002 年提出的XFAST 是一种改进的频域捕获算法[7-10],其基本思想是将一个很长的伪码分成M 个子段,每段长L 点,并将各子段的对应位置进行算术相加,组成一个新的长为L 点的重叠码。利用重叠码与接收信号进行相关运算,从而提高处理的并行性。XFAST 算法相对于常规的时域捕获算法,增加了重叠段数[8]、FFT 补零点数、FFT 点数等参数,如何实现对XFAST 中诸多参数的优化设计,是XFAST 设计过程中的难点。本文结合具体的工程实践,提出以单位相位搜索最小计算量为优化准则,给出XFAST 参数的优化设计方法,最后通过仿真验证本文优化准则及优化结果的正确性。

图 1 长码直捕时频二维搜索示意图Fig.1 Time and frequency planar search in long code direct acquisition
1 基于XFAST 的捕获原理
1.1 实现结构
中频AD 采样后的数字信号经过中频解调后,得到I 和Q 通道数据构成复信号进行FFT 变换,同时本地伪码经过重叠后,进行FFT 变换,结果取共轭后与接收信号FFT变换的结果相乘,然后进行反FFT变换,由频域相乘等于时域相关的原理,等效完成了时域接收信号和本地伪码的信号相关过程,经过平方律检波、非相干积累后进行捕获判决,若过门限则认为是成功捕获信号。
根据时域复指数相乘等效于频域偏移的原理,通过对接收信号FFT 变换后的结果进行循环移位,实现对不同频率偏移下的伪码相关值的搜索,具体如图2所示[11]。
1.2 伪码相位搜索策略
由信号处理的理论可知:设两相关序列长度均为L 点,常规频域计算线性相关值时,要求频域FFT 点长度PFFT≥2L-1。但对于XFAST,当重叠段数大于2时,可以不满足该约束条件,仅要求FFT 点数PFFT≥L,具体如图3 所示。
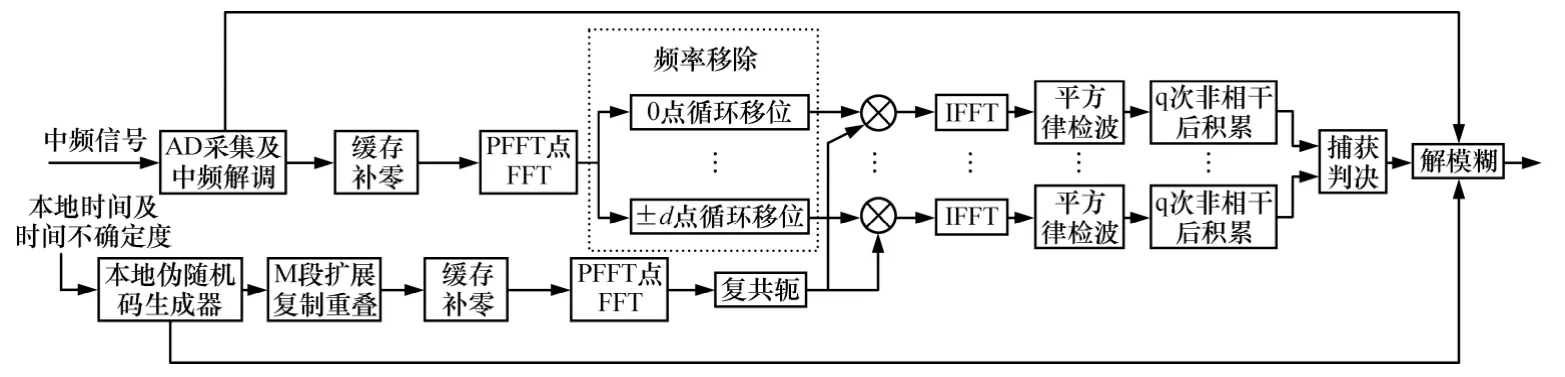
图2 XFAST 实现结构图Fig.2 Architecture of XFAST
扩展复制重叠计算相关的相位搜索原理如图3 所示,当本地序列与接收信号完全对齐时,对应搜索的相位为M,移位相关时,对应的搜索相位为M-1 个(图中阴影部分表示无效相位)。
由以上分析可知:进行一次扩展复制重叠的频域相关计算,搜索的伪码相位值为

其中:M 为本地伪码重叠段数;L 为相干累加点数;FFT 计算的点数要求为大于L 的最小的2 的幂次,即PFFT=(2n)min≥L。
2 性能分析
在工程实践中,通常是给定捕获概率和虚警概率,对参数进行优化设计。首先给出伪码多普勒影响下的捕获概率和虚警概率的解析表达式,并以此为约束条件,给出以单位码相位搜索计算量最小为优化目标的参数优化设计方法,以及在各种不同载噪比下的优化设计结果。
2.1 捕获概率和虚警概率
假设输入的中频解调后的复信号[12-13]为
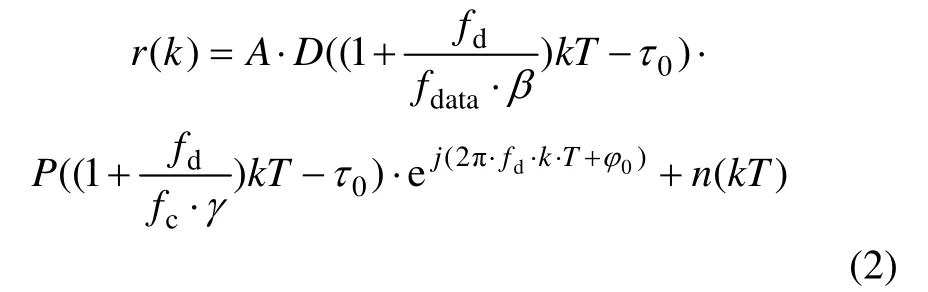
其中:T=1/fs,fs为中频下变频后的采样频率;A 为信号幅度;D(t)∈{+1,-1}为导航电文数据;P(t)∈{+1,-1}为长周期的精密测距码;fd为多普勒频偏,在二阶动态较小的情况下,假设在捕获时间内多普勒值是不变的;fdata为导航电文数据的符号速率;β 为载波频率和导航电文速率的比例因子;fc为伪码标称频率;τ0为未知的伪码相位传播时延;γ 为载波频率和伪码频率的比例因子;n(kT)为对功率谱密度为N0的窄带高斯白噪声采样,假设采样率为噪声带宽的整数倍(一般取为2 倍),则噪声采样点独立。
由于本地生成的伪码按照标称频率生成,由于未知的伪码多普勒的影响,故在积累过程中,接收到的信号的伪码相位与本地的伪码相位差会变化,同时由于FFT 分辨率的影响,相干积分后(即图中的IFFT 后的信号)的信噪比RB(j)为


其中:

由式(3)可知:当伪码相位差大于1 个码片时,相干积累的值已经没有增益了,此时对应的信噪比为0,故存在伪码多普勒时,不能简单地通过长时间的积分来提高信噪比。


则对应的捕获概率和虚警率分别为

对于虚警率给定的情况下,检测概率为

2.2 单位码片搜索计算量
长码直捕中,捕获概率和虚警概率确定的条件下,主要的衡量指标为捕获时间,捕获时间是完成频域和时域二维搜索的总时间,可以写成如下表达式:

其中:Tper_grid单元时频搜索的时间;Ndoppler_Num多普勒单元数; Ncode_Num伪码相位单元数; TAll所有时频二维搜索总时间。
对于XFAST 算法,由于不同的FFT 点数对应的频率搜索间隔不同(FFT 点数也是待优化的参数),故本文定义了单位搜索计算量即为搜索单位码片的各频率分量的相关值使用的计算量和。

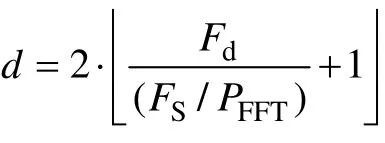
写成具体的表达式如下:

其中:PFFT=(2n)min>L(大于L 的最小2 的幂次)。
3 参数优化设计
在工程实现中,检测性能指标(Pf和Pd)给定,计算使单位计算量最小的扩展复制重叠段数M、中频积累时间L 和后积累点数q。由于无法给出确切的优化参数解析表达式,本文的参数优化通过数值仿真和搜索进行。
下面将分别给出不同载噪比和不同多普勒不确定度下的参数优化设计。
3.1 多普勒不确定度固定,不同载噪比
以GPS 的L1 P 码为例,采样率为20.47 MHz,多普勒不确定范围为6~6 kHz,载波和伪码的比例因子为154,捕获概率95%,虚警概率10-6,对应的不同重叠段数下的最小单位搜索计算量如图4 所示。从图4 可见:
(1) 不同载噪比条件下,在多普勒不确定范围固定时,存在单位搜索计算量最小值;
(2) 在载噪比较高时,并不是扩展复制重叠段数越多,对应的计算量越小,计算量一般首先随着扩展复制重叠段数的增加而降低,到达极值点后,再增加扩展复制重叠段数,计算量逐渐增加;
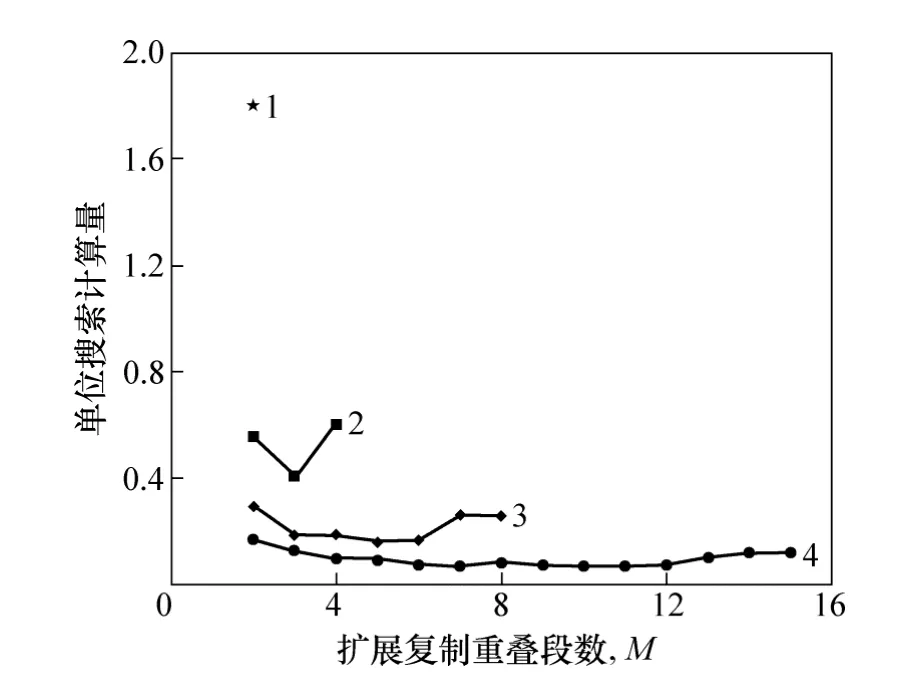
图4 相同的虚警、捕获概率以及不同载噪比下的单位搜索计算量Fig.4 Unit computation in condition of different carrier to noise ratio same false probability and detecting probability
(3) 载噪比越低,满足同样检测概率和虚警概率,所需的积累时间较长,由于伪码多普勒的影响,导致满足条件的扩展复制重叠段数受限,当载噪比为40 dBHz 时,只有M=2 时存在参数满足检测概率和虚警概率的要求。
(4) 当载噪比较高时,满足条件的不同的扩展复制重叠段数,单位搜索计算量相差较小。
表1 所示为多普勒确定条件下(-6~+6 kHz),不同载噪比下的最优参数设计。

表1 多普勒不确定度-6 kHz~+6 kHz,载噪比不同,单位搜索计算量最小对应的参数设置Table 1 Parameters of least unit computation with uncertainty Doppler of -6~6 kHz in different carrier to noise ratio
3.2 载噪比固定,不同多普勒不确定度
载噪比固定为46 dBHz,多普勒不确定度分别为±2 kHz,±4 kHz 和±6 kHz,捕获概率为95%,虚警概率为10-6时对应的单位搜索计算量分别如图5所示。
由图5 可以看出:多普勒越大,搜索计算量越大,可重叠段数越小。不同多普勒不确定度下的最小搜索计算量及对应的参数设置如表2 所示。

图5 相同的虚警、捕获概率,相同载噪比,不同的多普勒不确定度下的单位搜索计算量Fig.5 Unit computation in condition of different Doppler uncertainty, same false probability and detecting probability

表2 载噪比46 dBHz,多普勒不同,单位搜索计算量最小对应的参数设置Table 2 Parameters of least unit computation with carrier to noise ratio 46 dBHz, different Doppler
4 仿真验证
验证采用Matlab 模拟仿真,由于Matlab 中无法统计乘加计算的个数,仿真验证直接对程序运行时间进行统计,将运行时间除以对应的搜索码相位数,得到的单位搜索时间即等效反映了搜索计算量。根据表3 中的参数进行仿真计算,得到的具体运行时间如表3所示。
对表3 中的最后2 列结果进行比较,均以各自的第一个值进行归一化,得到理论计算值和实际仿真计算值如图6 所示。
由图6 可以看出:理论和仿真结果较为接近,从而可认为本文得到的搜索计算量是能够真实反映运算量大小的,本文的参数优化设计方法是切实可行的。
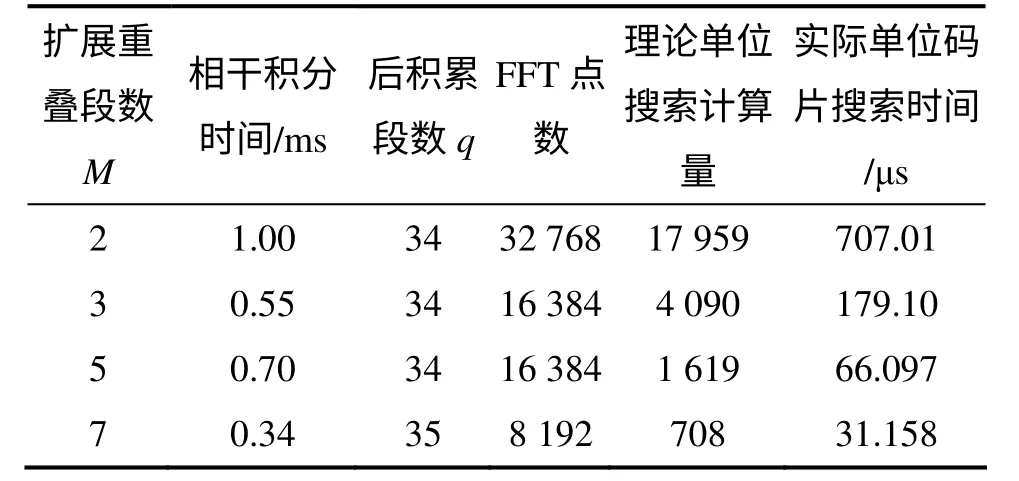
表3 搜索计算量仿真验证Table 3 Searching computation simulation validation

图6 仿真单位搜索计算量与理论单位搜索计算量比较Fig.6 Unit computation comparation of theoretics and simulation
5 结论
(1) 存在多普勒频移的条件下,扩展复制重叠引入的信噪比降低不能简单采用增加捕获总积累时间来补偿,XFAST 的使用有最低载噪比的要求。
(2) 重叠段数并不是越多越好,在输入参数及指标确定的条件下,存在极值点,可以根据本文给出的模型进行参数的优化设计。
[1] Elliott D K, Christopher J H. Understanding GPS: Principles and applications[M]. 2nd Edition. Boston: Artech House Inc, 2006:25-36.
[2] 任亚安, 王鹏, 许卫东, 等. GPS 中P(Y)码直接捕获技术的研究进展[J]. 全球定位系统, 2003(2): 2-9.REN Yaan, WANG Peng, XU Weidong, et al. Research development of the technique of direct P(Y)-code acquisition in GPS[J]. GNSS World of China, 2003(2): 2-9.
[3] 田明浩,冯永新,潘成胜. 一种基于P 码的频域直接捕获算法的研究[J]. 电子学报, 2007, 35(3): 549-552.TIAN Minghao, FENG Yongxin, PAN Chengsheng. Research of a method of direct acquisition based on P code in frequency domain[J]. Acta Electronica Sinica, 2007, 35(3): 549-552.
[4] LU Hu, LIAN Baowang, WU Peng, et al. Two dimension direct GPS signal acquisition based on unsymmetrical FFT[C]//4th IEEE Conference on Industrial Electronics and Applications.Xi’an, China, 2009: 1769-1772.
[5] JING P. Direct global positioning system P-code acquisition field programmable gate array prototyping[D]. Athens: Ohio University, College of Engineering and Technology, 2003:35-40.
[6] Sascha M S, Gordon J R P. Code acquisition for LEO satellite mobile communication using a serial-parallel correlator with FFT for Doppler estimation[J]. IEEE Trans on Vehicular Technology, 2001, 50(6): 1549-1567.
[7] Yang C. FFT Acquisition of Periodic, Aperiodic, Puncture, and Overlaid Code Sequences in GPS[C]//Proc of ION GPS 2001.Salt Lake City, US, 2001: 137-148.
[8] Yang C, Vasquez M J. Fast direct P(Y)-code acquisition using XFAST [C]//Proc of ION GPS 1999, Nashville, 1999: 317-324.
[9] LI Hong, LU Mingquan, FENG Zhenming. Direct P(Y)/M-code acquisition based on time-frequency folding technique[C]//ION GNSS 21st International Technical Meeting of the Satellite Division, Savannah GA, 2008: 167-173.
[10] YANG Chun, Nguyen T, Blasch E, et al. Post-correlation semi-coherent integration for high-dynamic and weak gps signal acquisition[C]//ION PLANS, Hyatt Regency Hotel Monterey,California, 2008: 1341-1349.
[11] LI Hong, CUI Xiaowei, LU Mingquan, et al. Dual-folding based rapid search method for long PN-code acquisition[J]. IEEE Transactions on Antennas and Propagation, 2008, 12(7):5286-5296.
[12] 梁坤, 施浒立. 高灵敏度GPS 捕获技术的分析与仿真[J]. 全球定位系统, 2007(6): 26-32.LIANG Kun, SHI Huli. Analysis and simulation of high sensitivity GPS acquisition techniques[J]. GNSS World of China,2007(6): 26-32.
[13] 李春霞, 王飞雪, 郭桂蓉. 一阶动态条件下伪随机码信号相关函数研究[J]. 电子学报, 2007, 35(9): 1789-1793.LI Chunxia, WANG Feixue, GUO Guirong. Correlation of PN spread spectrum signal under first-order dynamics[J]. Acta Electronica Sinica, 2007, 35(9): 1789-1793.
[14] 王飞雪, 郭桂蓉. 二相编码信号分段相关-视频积累的最优中频积累时间[J]. 国防科技大学学报, 1999, 21(1): 71-75.WANG Feixue, GUO Guirong. The optimum if integration time length for binary phase-coded signals detection based on segment correlation-video integration method[J]. Journal of National University of Defense Technology, 1999, 21(1): 71-75.
