基于附面层的摩擦阻力数值算法研究

彭 聪

(成都大学生物产业学院，四川 成都 610106)

基于附面层的摩擦阻力数值算法研究

彭 聪

(成都大学生物产业学院，四川 成都 610106)

利用附面层的速度型求解壁面的空气剪切应力，进而求得摩擦阻力，由此计算了一维层流平板边界层和二维层流NACA0012翼型的摩擦阻力.平板边界层计算结果同布拉修斯理论解相比较，吻合性良好.翼型计算结果同实验数据比较发现，小攻角气流不产生分离的情况下，摩擦阻力值与实验数据接近，随着迎角增大，分离区的扩展，压差阻力的比重增加，计算误差明显增加.

摩擦阻力;附面层;数值计算;空气粘性

0 引言

从20世纪70年代末开始，在先进理论方法和成功工程实践的基础上，由于计算流体动力学(Computational Fluid Dynamics，CFD)计算方法的不断突破和计算机技术的快速发展，CFD进入了蓬勃发展的新时期，开始越来越多地应用到航空航天飞行器的研究和设计中［1－4］.目前，阻力计算一直是CFD中的一大难题和研究热点，根据其产生机理，阻力主要分为压差阻力和摩擦阻力2种.压差阻力是飞行器各部分表面受到的压力在速度方向上的合力，又分成波阻、涡阻、型阻等;而摩擦阻力是飞行器各部分表面受到的剪切力在速度方向的合力，它是由空气的粘性而引起的.目前的CFD方法对于流场中物体表面压力的分布能得到很好的计算结果，在压差阻力的计算方面精度较高，但对于摩擦阻力的计算却存在一定难度，这是因为摩擦阻力的计算对CFD有较高的要求，需要计算出飞行器合理的流场结构，尤其需要正确捕捉壁面边界层内的速度型以准确计算壁面处的剪切力［5－6］.平板绕流问题是附面层流动最简单也是最重要的情况，而对于曲面绕流，只要不发生显著分离，摩擦阻力与平板情况相差不多.本研究采用层流平板边界层和NACA0012翼型边界层来验证摩擦阻力计算的有效性及精度.

1 摩擦阻力计算方法

1.1 控制方程

本研究利用商用Fluent软件求解N-S方程，不考虑体积力和外部热源，其形式［6］为，

式中，Q为守恒变矢量;f，g，h分别为x，y，z坐标方向的通量.

1.2 壁面摩擦阻力

摩擦阻力由切向应力引起，并跟附面层的速度型相关.切向应力为，

式中，μ为流体粘性系数，摩擦应力τ与附面层间的切向速度u的变化有关.

摩擦阻力为壁面摩擦应力xF的积分，其形式为，

平板摩擦阻力系数CF根据定义为，

1.3 壁面应力的精度

壁面应力τw的计算采用二阶精度的中心差分格式，其形式为:

2 算例及分析

2.1 层流平板附面层及摩擦阻力计算

层流平板附面层的计算模型如图1所示.网格数为106×50(流向 ×法向)，远场为4倍平板长.为准确地模拟粘性效应，附面层内布置了至少4个网格点.自由来流条件为:来流速度Ma∞=0.3，雷诺数 ReL=1.0 ×105，攻角 α =0°，研究网格质量对流场及摩擦阻力的影响.表1为平板摩擦阻力计算结果，并与布拉修斯解进行了比较，图2为平板各占位的速度型.

图1 层流平板附面层计算网格

表1 摩擦阻力计算结果

图2 层流平板各站位的速度型

从图2可以看出，平板附面层内各站位的速度型与布拉休斯解曲线拟合得很好，由此计算得到的阻力系数值很接近.但由于阻力系数值本身为一个小量，网格的粗细和计算格式的粘性分辨率对计算精度都产生影响.从计算效率来说，对于本算例，附面层内布置3～4个网格点就能很好地捕捉速度型.此对于大型网格计算具有指导意义，但对于复杂外形，网格数量更大的情形，还需要进一步验证.

2.2 NACA0012翼型附面层及摩擦阻力计算

NACA0012翼型附面层的计算模型如图3所示.网格数为497×100(C型网格)，远场为10倍弦长.边界层内同样布置了4个网格点.自由来流条件为:来流速度 V∞=21.1 m/s，雷诺数 ReL=1.44×106，攻角分别为 0°、2°、4°、8°时，着重研究翼型绕流情况对摩擦阻力计算的影响.

图3 NACA0012翼型计算网格

图4、图5、表2为模型在不同攻角下的计算与实验结果.

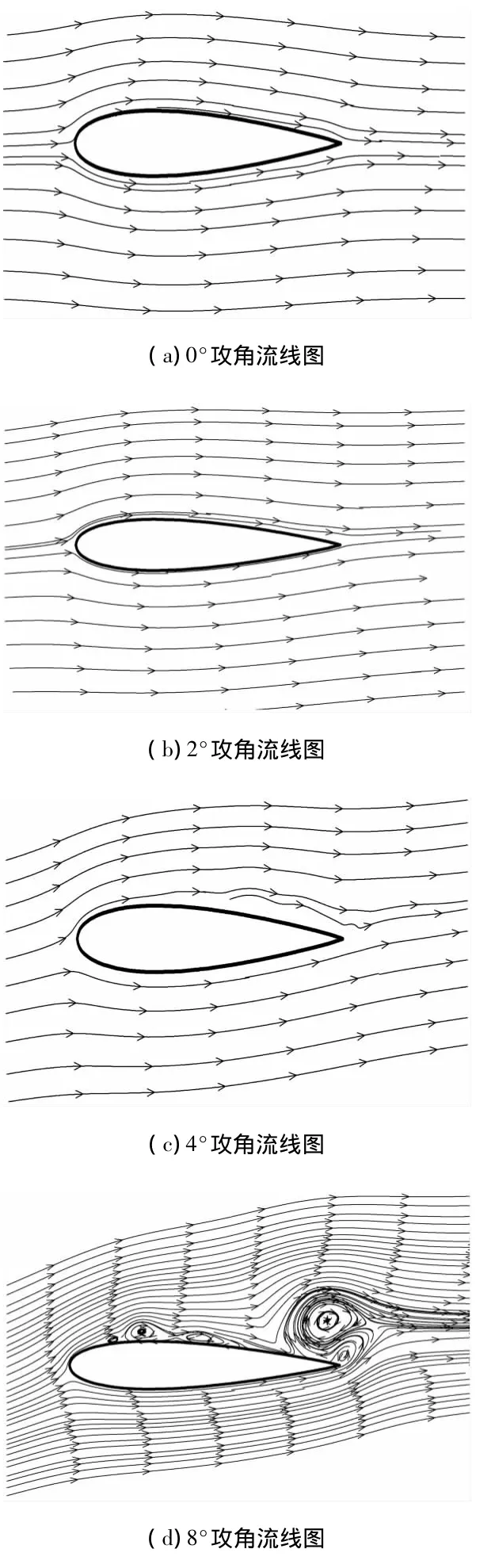
图4 不同攻角下的流线图

从图4中的流线可以看出，0°和2°攻角的流场情况较为相似，气流均贴着翼型呈明显的层流状态;4°攻角时，翼型对来流产生扰动，上翼面1/2弦长位置出现局部气泡，但气流未出现明显分离，至后缘气流再附于翼型表面，基本保持层流状态;8°攻角时，扰动进一步增强，上翼面气泡出现位置向前缘移动，且出现明显的分离趋势，至后缘与下翼面绕流形成分离涡结构.

图5 NACA0012翼型计算结果同实验数据的比较

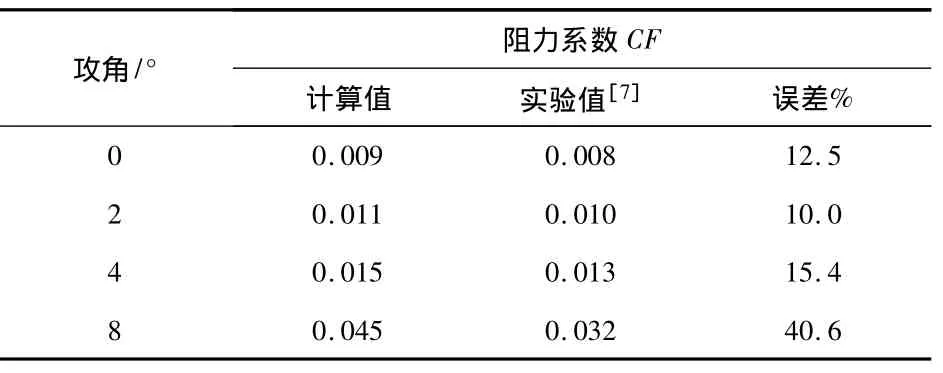
表2 NACA0012翼型在不同攻角下阻力系数计算值与实验值的比较

此外，从图4中可看出，在对称流动时，驻点位于翼的前缘，翼型绕流为附体状态，阻力的主要贡献为空气粘性影响的翼型表面很薄的附面层，表现为摩擦阻力，表面压强分布对阻力影响很小.层流状态下，摩擦阻力也很小，即使在很小的攻角情况下，只要绕流不产生分离，摩擦阻力的增加不明显.随着迎角的增大，驻点向下翼面移动，并逐渐后移，上翼面最大速度点向前缘移动.对于圆头较厚翼型，在中等迎角下，上翼面靠近后缘的附面层在逐渐增大的逆压梯度作用下发生局部分离.随着攻角增加，分离区向前扩展，当迎角达到某个临界值后上翼面的附体流动被彻底破坏，翼型表面产生很大的压强差，导致升力降低，阻力显著增大.由此可见，层流到完全破坏的过程，压差阻力的贡献越来越大.

同时，从图5与表2可以看出，在小攻角的层流状态下，根据摩擦阻力计算的阻力系数与实验值接近，误差约为10%.攻角增大后，随着分离气流的出现，压差阻力的增加，阻力系数计算误差也显著增加，4°攻角时为15%，8°攻角时达40%.这主要有2方面原因:一是分离气流的速度方向不再沿着翼型流向，法向速度分量的压力贡献产生的合力增加;二是分离气流本身的不稳定性，计算模型在模拟分离流动的精度不够而造成.采用式(2)的阻力计算方法建立在精确模拟流场特性的基础上，对此，需寻求更好的计算模型和计算精度来进行模拟求解.

3 结论

本研究基于对一维平板边界层和二维NACA0012翼型采用数值方法得到的摩擦阻力计算结果，可以看出:采用低阶精度格式计算低速条件下的层流边界层能够得到精度很高的摩擦阻力值，与理论解和实验数据相当吻合;采用壁面摩擦阻力计算方法在层流状态下能够得到准确的结果，但随着流动分离的出现，压差阻力的比重增加，采用本方法得到的结果误差增大，适用性降低.基于上述2点，本研究下一步的工作思路是研究湍流状态下的摩擦阻力计算方法，包括选择合适的湍流模型，采用更高精度的计算格式，等等.

［1］Tinoco E N.An assessment of CFD prediction of drag and other longitudinal characteristics［C］//39th Aerospace Sciences Meeting and Exhibit.Reno，NV:AIAA，2011:1002.

［2］Peavey C.Drag prediction of military aircraft using CFD［C］//38th Aerospace Sciences Meeting and Exhibit.Reno，NV:AIAA，2000:383.

［3］叶建，林国华，邹正平，等.低雷诺数下二维翼型绕流的流场特性分析［J］.航空动力学报，2003，18(2):38 －45.

［4］侯志勇，石磊，聂万胜.对称翼型低速绕流流场特性的数值分析研究［J］.科学技术与工程，2009，9(18):5610－5613.

［5］周丹，禹建军，闫超.层流平板摩擦阻力的数值计算［J］.北京航空航天大学学报，2007，52(6):663－667.

［6］闫超.计算流体力学方法及应用［M］.北京:航空航天大学出版社，2007.

［7］Rice M S.Hand book of airfoil sections for light aircraft［M］.Milwaukee，WI:Aviation Publications，1976.

Study on Numerical Algorithm for Skin Friction Based on Boundary Layers

PENG Cong
(School of Biological Industry，Chengdu University，Chengdu 610106，China)

In order to obtain skin friction of the boundary layers，we adopt the air velocity model to solve the viscid stress.The skin frictions of two cases，1-D laminar flat-plate boundary layer and 2-D laminar NACA0012 airfoil，are calculated by this method.The result of the flat-plate boundary layer matches Blasius solution quite well.Comparing the result of the airfoil calculation with the experimental data，we find that the calculation precision is acceptable at a relatively small angle of attack without airflow separation.As the angle of attack increases and the separation region expands and the proportion of pressure resistance increases，the calculation errors of this method will increase significantly.

skin friction;boundary layer;numerical calculation;air viscosity

V211.3

A

1004－5422(2014)01－0029－04

2013－09－05.

彭 聪(1980—)，女，从事计算机软件编程与算法研究.