六维欧式空间球面曲线的一个几何性质

潘 虹，杜 柯，李占芳

(信阳师范学院数学与信息科学学院，河南 信阳 464000)

六维欧式空间球面曲线的一个几何性质

潘 虹，杜 柯，李占芳

(信阳师范学院数学与信息科学学院，河南 信阳 464000)

为了探究球面曲线的几何特征，对欧式空间的公式进行了研究，将欧式空间的公式推广至6维欧式空间，给出了判定一条曲线是球面曲线的充分必要条件.

公式;球面曲线;6维欧式空间

0 引言

Frenet标架和Frenet公式是曲线论基本定理的依据，也是阐明曲线在一点邻近结构的重要工具，其在曲线论中起着关键的作用.本研究根据曲线基本向量的微商与基本向量之间的特定关系，在3维欧式空间 Frenet标架［1－4］和 Frenet公式的基础上，对R4{5}、R5{6}中的欧式空间球面曲线做了进一步的探讨并给出了相应的结论，在此基础上，构造出6维欧式空间下沿空间曲线的Frenet标架，推广了Frenet公式，并利用推广后的Frenet公式得到判定空间曲线是球面曲线的一个充分必要条件，并给出相应证明.

1 主要结果

引理1 在3维欧式空间中，Frenet公式可表示为，

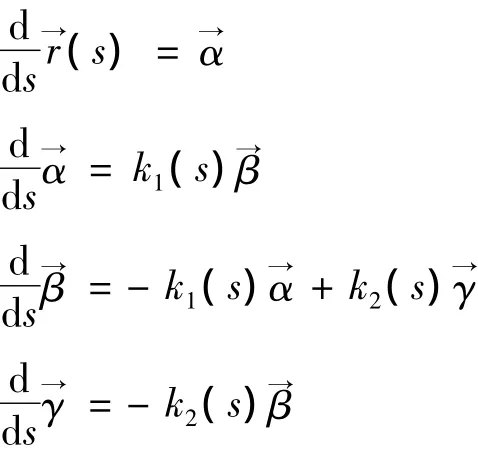
根据这组公式的系数组成反方阵的特点，可构造出6维欧氏空间下沿空间曲线的Frenet标架

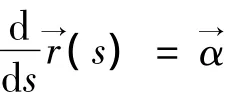
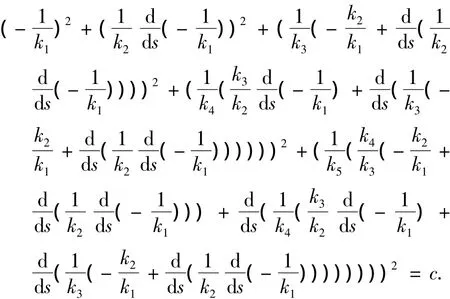
证明 根据空间曲线曲率的定义和球面曲线的性质来证明这个定理.

1)必要性.

由6维欧式空间的正则曲线出发，推得5个曲率之间的关系.设球面方程为，

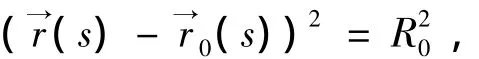
对上式两端分别求导，得到，

对上式两端分别求导，得到，

上式两端作比较可得到，

解之得，

将上式代入方程得到，

两边同时取模，可得到结论.

2)充分性.

由于，

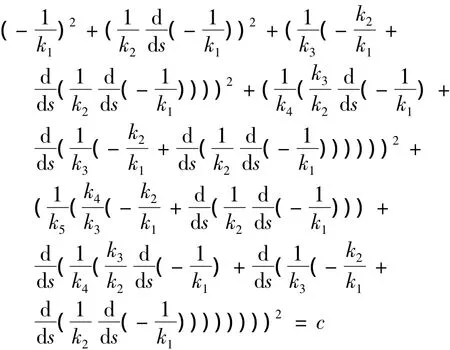
对上式两端分别求导得，

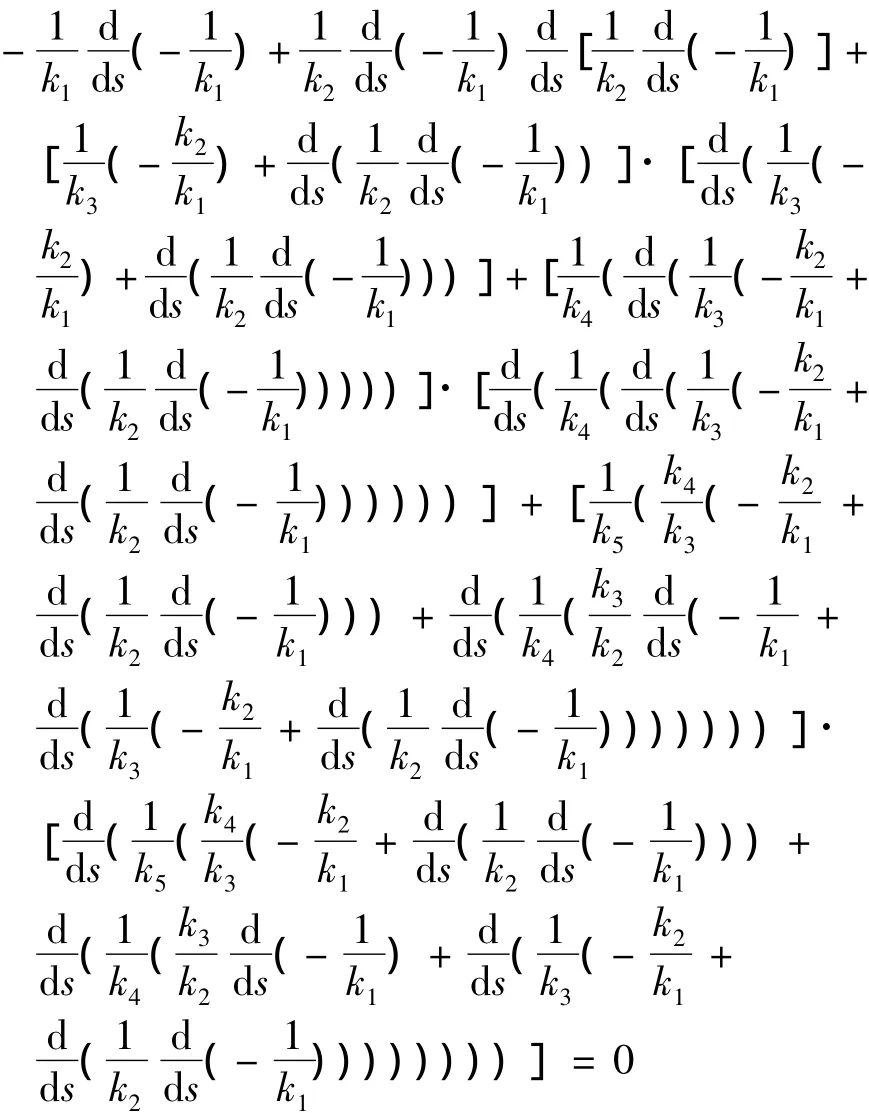
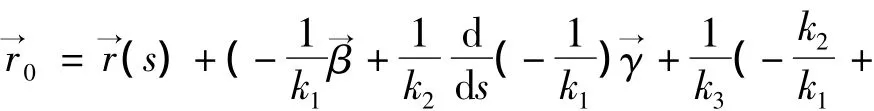
对上式两端分别求导得，

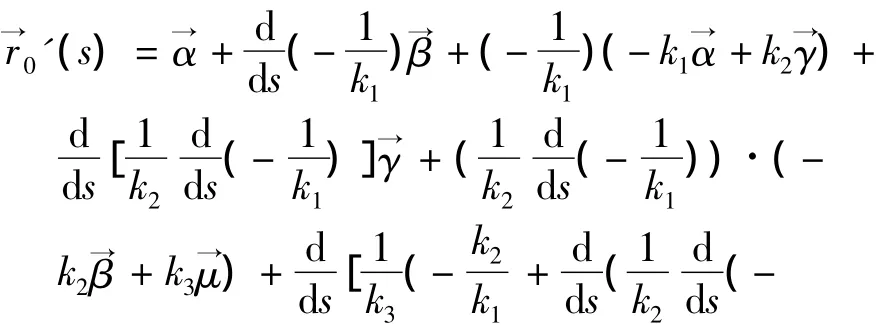
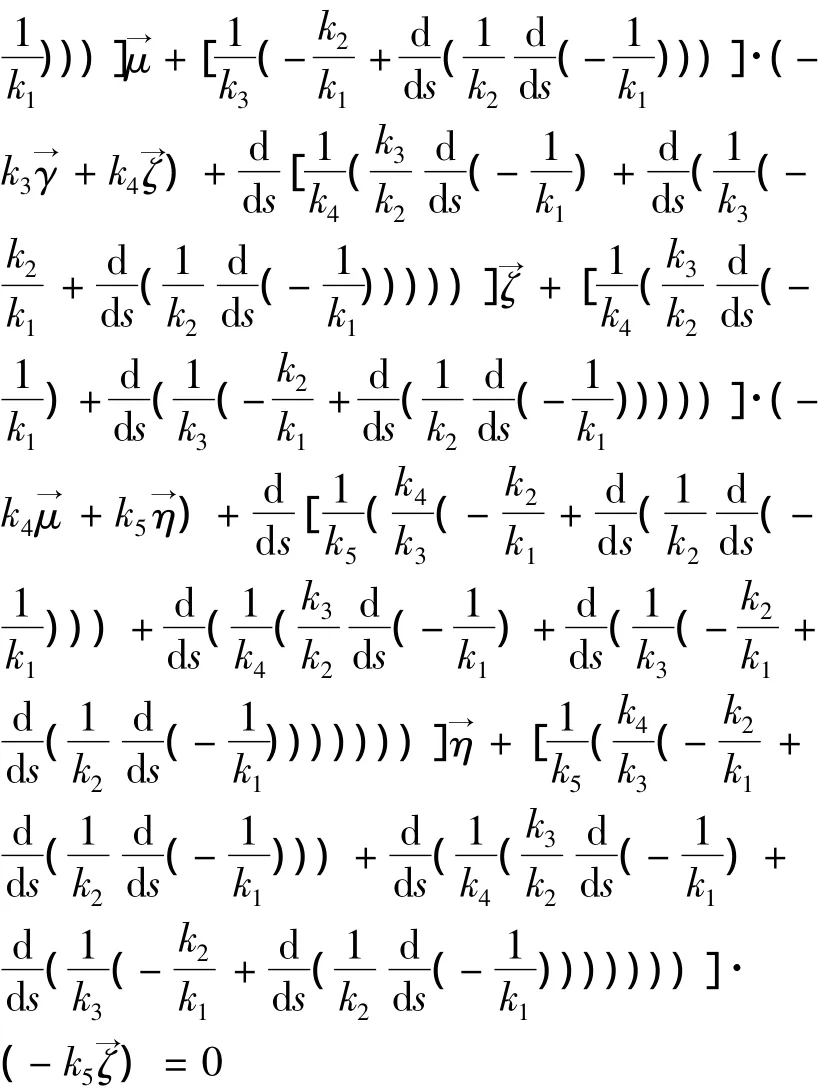
因此，

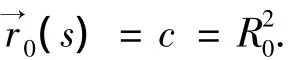
命题得证.

［1］梅向明，黄敬之.微分几何［M］.北京:高等教育出版社，1990.

［2］陈维恒.微分几何［M］.北京:北京大学出版社，2003.

［3］刘学泳.空间两曲线的基本向量之间关系研究［J］.湘潭师范学院学报，2004，4(1):34 －35.

［4］吴大任.微分几何讲义［M］.北京:人民教育出版社，1982.

［5］潘虹，李林栋，张超楠.四维欧式空间的一个几何性质［J］.高师理科学刊，2013，33(1):5 －7.

［6］薛艳日方，冯艳丽，李玲玲.五维欧式空间的一个几何性质［J］.成都大学学报(自然科学版)，2012，31(4):327 －330.

One Geometric Property of Spherical Curves in 6-dimensional Euclidean Space

PAN Hong，DU Ke，LI Zhanfang
(School of Mathematics and Information Science，Xinyang Normal University，Xinyang 464000，China)

In order to explore the geometrical characteristics of spherical curves，this paper discusses the Frenet formula of Euclidean space.The Frenet formula of Euclidean space is extended to 6 dimensions，and a sufficient and necessary condition is presented to judge whether a space curve is a spherical curve.

Frenet formula;spherical curve;6-dimensional Euclidean space

O186.1

A

1004－5422(2014)01－0023－03

2014－01－02.

国家自然科学青年基金(11201400)、河南省自然科学基金(132300410056)资助项目.

潘 虹(1980—)，女，硕士，讲师，从事微分几何与一般拓扑学研究.