基于一维离散小波变换的心电信号降噪研究

孔令杰

(菏泽学院物理与电子工程系，山东菏泽274015)

0 引言

心电信号是人体生物医学信号中一种非常重要的信号，对它进行深入的研究一直是生物医学信号处理领域中的热点.但是由于检测仪器、人体等内外环境的多种因素的影响，使得在实际采集的心电信号中不可避免的混入了各种噪声，如工频干扰、肌电干扰等.所以采集到的心电信号一般具有随机性和强背景噪声，是一种信噪比较低的非平稳随机信号，为了达到能从心电信号中提取更多反映人体全身性和综合性的生理病理特征信息的目的，在处理和分析心电信号之前对其进行降噪处理就是一项十分重要的工作[1-2].

小波变换是一种窗口面积固定但时间窗和频率窗都可变化的时频局部化分析方法.因此，小波变换具有了多分辨率分析的特点，可以在时频两域同时具有表征信号局部特征的能力.简单来讲，即在低频部分具有较高的频域分辨率和较低的时间分辨率，而在高频部分具有较高的时间分辨率和较低的频域分辨率.正是这两种特性使得小波变换被誉为信号处理分析领域中的“数学显微镜”，同时这两种特性也与低频信号变化缓慢而高频信号变化迅速的特点相符合，使得小波变换具有了对信号的自适应性[3].鉴于此，该文提出一种基于小波变换的心电信号降噪方法，并通过实验研究验证了该方法的有效性和可行性，从而为心电信号特征信息的提取提供了一种新的研究思路.

1 一维离散小波变换

1.1 一维离散小波变换的分解算法

在信号处理分析领域中，一维离散小波变换的实现算法是Mallat算法，即先对较大尺度的信号进行小波变换，再选取其中的低频部分在原尺度的1/2尺度上再进行小波变换[4].Mallat算法又称为快速小波变换的算法(简记为FWT)，为方便描述一维离散小波变换理论，该文采用滤波器的观点来进行介绍，FWT分解算法的流程如图1所示.

FWT分解算法的具体过程如下:

1)在图1a中，从原始信号S开始，产生两组参数，一组是作用分解低通滤波器Lo-D得到的近似系数cA1，另一组是作用分解高通滤波器Hi-D得到的细节系数cD1，这两组参数都是原始信号S在滤波器作用下以尺度为2的下采样.

2)在图1b中，采用同样的做法，把其中的近似系数cA1作为“原始信号S”再次分解，并以此类推根据所需要分解的层数对信号进行分解.

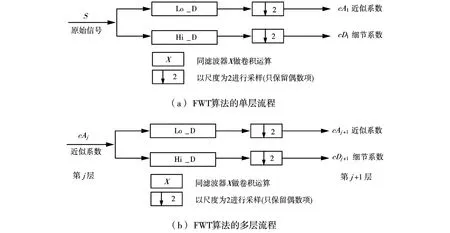
图1 FWT分解算法的流程

1.2 一维离散小波变换的重建算法

重建运算是小波变换的逆变换，也就是把分解得到的近似系数和细节系数进行叠加以得到原始信号.它与小波变换分解过程相比，重构过程首先从尺度最低的近似系数cAj和细节系数cDj开始，通过作用低通重构滤波器Lo-R和高通重构滤波器Hi-R恢复上一尺度的近似系数cAj－1，以此类推，把这个过程重复继续下去，直到得到原始信号S[5].FWT重建算法的流程如图2所示.

图2 FWT重建算法的流程

2 小波降噪原理及实现

2.1 小波降噪的基本思想

该文采用如下模型来表示一个含噪的一维信号

式中，s(t)代表原始信号，n(t)代表服从N(0，σ2)的高斯白噪声.

小波降噪的基本思想是:根据式(1)，对信号f(t)作一维离散小波变换，考虑正交小波变换具有较强的数据相关性，因此它在实现小波变换时，能够将信号f(t)的小波系数一部分变换为较大幅值且与信号相对应的小波系数，而将另一部分变换为较小幅值且与噪声相对应的小波系数.这样一来，对信号f(t)进行一维离散小波变换分解后，信号的小波系数就要大于噪声的小波系数，然后就可以选择一个恰当的临界阈值λ，使其产生如下两种情况:1)若一维离散小波变换后得到的小波系数高于设定的临界阈值λ，就可以认为分解的小波系数主要是由信号产生的，则此时可保留这个小波系数或者按照某一固定量向零收缩这个小波系数;2)若一维离散小波变换后得到的小波系数低于设定的临界阈值λ，就可以认为分解的小波系数主要是由噪声产生的，则此时可直接舍弃这个小波系数.经过上述步骤，再用由临界阈值λ处理后的小波系数进行小波重构，就可去除信号f(t)中的噪声信号n(t)[6].

2.2 小波降噪的步骤与方法

通常来说，一维信号的降噪算法可以包含如下3个步骤[7].

1)信号的小波分解

首先选择合适的小波基和分解层数，然后按照Mallat算法对信号进行小波变换.

2)小波高频系数的阈值量化

选择一个恰当的阈值对各个分解尺度下的小波高频系数进行阈值量化处理.

3)一维小波重构

按照Mallat算法，将小波分解的底层系数和各层高频系数进行一维小波重构.

在上述3个步骤中，如何选择恰当的阈值进行量化处理是最关键的问题，它在某种程度上与信号降噪质量的高低有着直接关系.

此外，小波变换进行降噪处理一般采用以下3种方法.

1)默认阈值降噪处理

该方法先借助ddencmp函数生成信号的默认阈值，再利用wdencmp函数实现信号的降噪处理.

2)软阈值降噪处理

在实际的信号降噪处理过程中，往往通过经验公式获得软阈值，而且与默认阈值相比，它具有较高的可信度，该方法在进行阈值量化处理时可调用wthresh函数.

3)强制降噪处理

该方法采用将小波分解后的高频系数全部置零的方式，来滤除信号中所有的高频部分，然后对信号进行重构运算.虽然该方法的降噪处理过程比较简单，且降噪后的信号比较平滑，但缺点是极易失去信号中的有用信息.

2.3 小波分解尺度的选取

在信号降噪处理过程中，最大分解尺度j一般取值为3～5.一方面，j越大，此时信号和噪声呈现出的不同特性就越明显，则越有利于信噪分离;另一方面，对于信号重构过程来讲，j越大，意味着失真越大，即重构误差越大.显然提高信噪分离与降低重构误差这是一对矛盾，必须选择适当的分解尺度j来兼顾二者.有研究表明，所选小波分解尺度j应视原始信号中的信噪比(SNR)值的大小而定，且对于一般的信号而言，若SNR＞20，则取j=3;否则，取j=4为好.

2.4 小波降噪性能的评价指标

为了更加精确的描述小波变换的降噪性能，该文又引入信噪比(SNR)和自相关系数(AC)作为评价指标，其表达式分别为[8-9]:

1)信噪比(SNR)

2)自相关系数(AC)

其中:xi为原信号序列，x为其平均值;yi为降噪信号序列，y为其平均值;N降噪信号与原信号的长度.SNR值反映了降噪后信号中噪声成分的多少，SNR值越大，说明信号降噪以后，保留的噪声成分越小;AC值反应了降噪后信号与原信号之间的相关程度，AC值越大，说明降噪信号与原信号之间的相关程度越高.

3 心电信号的降噪处理实验及性能分析

为验证上述方法的可靠性和可行性，该文采用MATLAB7.1软件实现编程，并采用MIT/BIH心律失常库中的心电信号数据文件105.dat前6 s的心电数据为例进行检验，该心电信号数据文件中已含有各种强噪声(如工频干扰、基线漂移、肌电干扰和运动伪迹等).原心电信号如图3所示.

从图3中可以看出，该心电信号不够平滑，尤其在P、S和T段含有大量高频噪声，这直接影响着提取心电信号特征信息的准确性，所以应对这段心电信号进行降噪处理.由于人体心电信号是一种微弱信号，信噪比较低，故该文选用db3小波基对心电信号进行4层分解，小波分解后的近似系数和细节系数如图4所示，降噪处理后的心电信号如图5所示.

图3 原心电信号

图4 小波分解后的近似系数和细节系数结果

由上述实验结果可见:与原始心电信号相比，用默认阈值降噪后得到的心电信号，其重构结果的光滑性最好，且降噪后心电信号的P、Q、R、S、T波形基本保持原有心电特征;而用软阈值降噪后得到的心电信号，虽然其重构结果的光滑性较好，但重构结果也不可避免地丢失了一些突变点处的有用信息，包括R波出现严重削峰、QS波出现削峰和变形等.产生上述现象的原因在于软阈值估计的小波系数与真实小波系数之间存在某一恒定的偏差，正是这一偏差直接影响了重构信号与真实信号之间的逼近程度;对于用强制降噪后得到心电信号，其重构结果的光滑性相对较差，且局部位置存在振荡现象[10].

采用SNR和AC值两种指标分别对使用db3小波基降噪后的心电信号进行评价，评价结果如表1所示.由AC值可见，基于小波变换降噪后的心电信号与原心电信号之间高度相关，但尤其以采用默认阈值降噪效果最为显著;又因其SNR值最大，故降噪后心电信号中保留的噪声成分最小，这也与图5a中的结果相吻合.

表1 两种指标的评价结果

综上所述，基于小波变换的降噪方法能够有效地抑制心电信号中的噪声，较好地保留了其原始信息，降噪性能优越，从而为实现心电信号特征信息的提取和辨识奠定了理论基础.

4 结语

针对心电信号中存在的噪声问题，该文利用小波变换方法进行了具体分析，得到如下结论:使用小波分解与重构算法，能够同时有效地去除心电信号中常见的肌电干扰、工频干扰和基线漂移3种噪声，并能较好地保留原心电信号的特征信息，从而有利于实现心电信号特征信息的提取和辨识.同时，实验研究的结果也表明采用SNR和AC值两种指标评价小波降噪性能具有有效性和可行性，可以普及到任何心电信号中，也可在其他信号降噪处理中使用.

[1] 高清维，李海鹰，庄镇泉，等.基于平稳小波变换的心电信号噪声消除方法[J].电子学报，2003，32(2):235-240.

[2] 王玉静，宋立新，康守强.基于EMD和奇异值分解的心律失常分类方法[J].信号处理，2010，26(9):1423-1427.

[3] 胡昌华，张军波，夏军，等.基于Matlab的系统分析与设计:小波分析[M].西安:西安电子科技大学出版社，1999.

[4] 张德丰.MATLAB小波分析[M].北京:机械工业出版社，2009.

[5] 飞思科技产品研发中心.小波分析理论与MATLAB7实现[M].北京:电子工业出版社，2005.

[6] 林克正，李殿璞.基于小波变换的去噪方法[J].哈尔滨工程大学学报，2000，21(4):21-23.

[7] 付明.小波变换在信号降噪中的应用研究[J].微计算机信息，2008，24(1):237-238.

[8] 顾远.心电信号去噪及效果评价研究[D].天津:天津理工大学，2012.

[9] 罗强，田化梅，罗萍，等.基于平稳小波变换的心电信号去噪研究[J].计算机与数字工程，2006，34(6):67-69.

[10] 徐洁，王阿明，郑小锋.基于小波阈值去噪的心电信号分析[J].计算机仿真，2011，28(12):260-263.