附合导线近似严密两种平差方法点位精度的对比

2014-03-28杨小平

杨凌职业技术学院学报 2014年1期

李飞，杨小平

(杨凌职业技术学院，陕西杨凌 712100)

0 引言

附合导线包括方位附合导线、坐标和方位附合导线、坐标附合导线(又称无定向附合导线)。附合导线在工程测量中有着广泛的应用，尤其在测图中更是经常用到，而附合导线的平差计算是其中的一个重要环节，本文就是利用近似、严密平差原理结合具体附合导线(坐标和方位附合导线，其在工程中应用最多)实例计算待定点的点位精度，通过对比，提出两种方法的应用领域。

1 平差原理

1.1 近似平差原理

①角度闭合差的计算与调整；②坐标方位角的推算；③坐标增量闭合差的计算与调整；④导线坐标计算；⑤精度评定。

1.2 严密平差原理

①确定必要观测数t，设置t个独立的参数(一般设未知点的坐标为参数)；②求参数的近似值；③求近似坐标方位角、近似距离和近似坐标增量；④列角度和边长的误差方程式；⑤组成法方程；⑥解算法方程，参数的改正数；⑦计算改正数和平差值；⑧精度评定。

2 坐标和方位附合导线算例

近似平差方法：

①角度闭合差的计算与调整。

角度闭合差为：fβ=αAB+β1+β2+β3+β4+

β1-4×180 °-αCD=12 ″

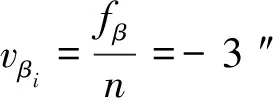
则，调整后的角度为：(结果见表2) 。

表1 观测数据

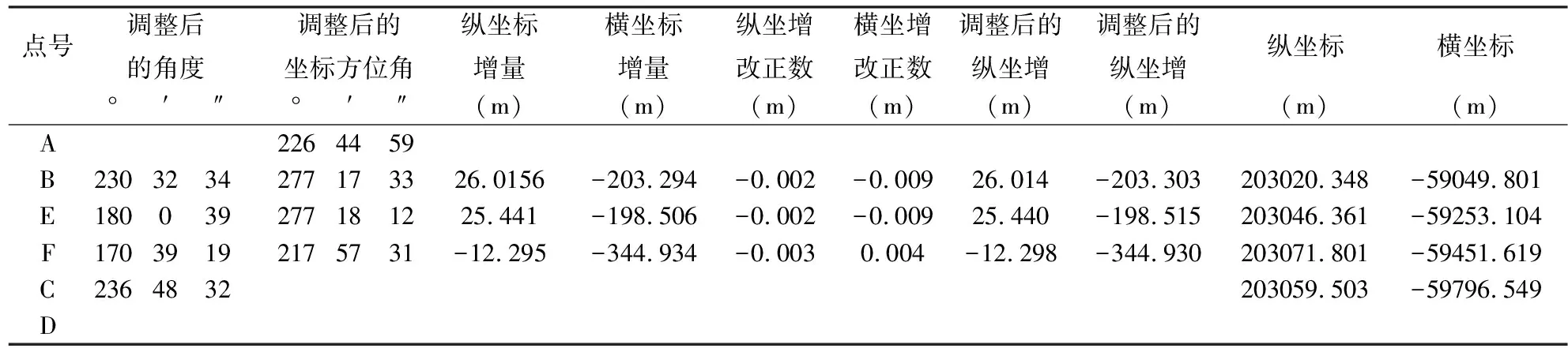
表2 附合导线计算表

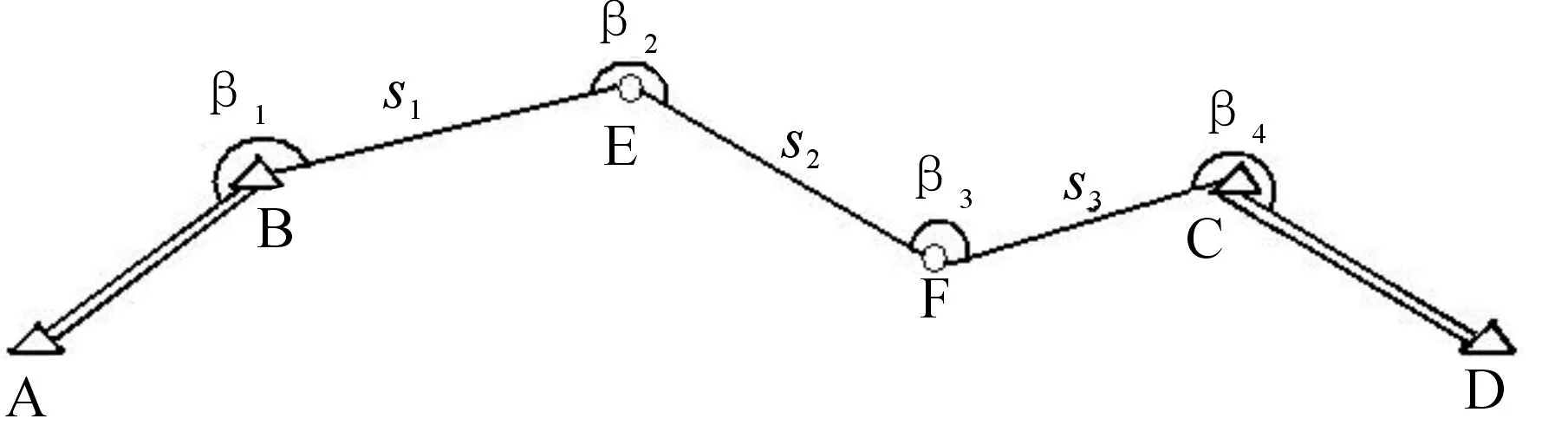
图1 坐标和方位附合导线图

②坐标方位角的推算。

各边方位角为：

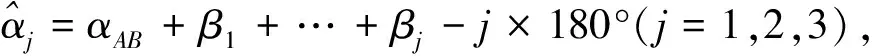
③坐标增量闭合差的计算与调整。

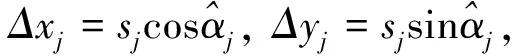
④导线坐标计算(结果见表2)。

坐标闭合差分配后，第k点的坐标计算式为：

⑤精度评定。

顾及观测角为等精度独立观测值，取σβ=±5″，由协方差传播律可得调整后方位角的方差——协方差阵为：

边长的方差——协方差阵为：

G1=[B1cosα1-A1cosα2-A1cosα3],

K1=[B1sinα1-A1sinα2-A1sinα3],

G2=[B2cosα1B2cosα2-A2cosα3],

K2=[B2sinα1B2sinα2-A1sinα3],

将数据带入得：S=750.235 m，A1=0.273,B1=0.727,A2=0.540,B2=0.460

根据R,T系数阵，计算2个导线点的近似平差坐标的方差——协方差阵，得

严密平差方法：

本附合导线中，必要观测数t=4，选定待定点坐标平差值为未知数，即：

①计算待定点的近似坐标。

②计算近似坐标方位角，近似坐标增量，近似距离。

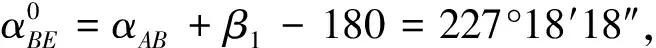
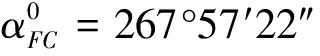
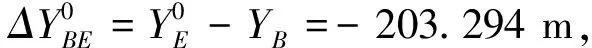
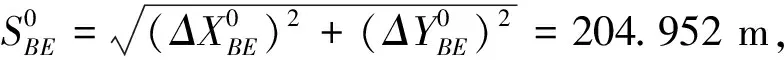
③确定观测值的权。

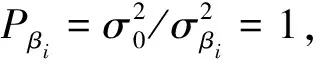
④列误差方程式，列出B和l。

角度误差方程式为：

边长误差方程式为：

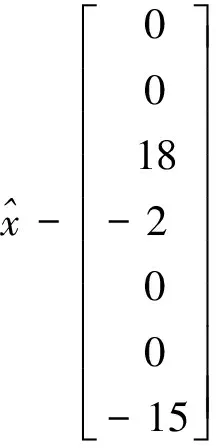
⑤组成法方程为：

⑥解法方程，得未知数的值及未知数的协因数阵为：

⑦计算参数的平差值、改正数和观测值平差值。

参数的平差值为：

203071.803-59451.609]T(m)

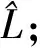
⑧精度评定。

a. 单位权中误差：

b.E点坐标及点位中误差：

±3.35 mm;

±6.57 mm;

c.F点坐标及点位中误差：

±4.08 mm;

±7.39 mm;

精度对比表(见表3)。

3 结语

本文通过单一附合导线实例对近似严密平差两种方法计算点位精度进行了对比，表三数据表明：两种方法精度相差不是很大，严密平差方法约束条件较大，由解算过程可知，近似平差边长观测值无误差，所以在实际的工程中，应根据边长观测的精度来选取平差方法，若观测边长相对角度精度高，选近似平差，若观测边长相对角度精度低，选严密平差。