实际热声热机微热力学循环性能优化

林杰，吴锋，费锦华，汪拓

（武汉工程大学机电工程学院，湖北武汉430073）

0 引言

热声热机是一种完全新型的热机［1－5］，与传统的热机相比，由于其无运动部件，消除了因机械摩擦而存在的磨损与振动；另外，热声热机中使用的工质是对环境无害的惰性气体，从而消除了因有害气体（如氟利昂）对环境的污染问题.热声热机工作机理为热声效应机理：声与热在满足一定条件下的相互转换现象，即热能转换成声能或者声能转换成热能的现象.基于热声热机的诸多优点，国内外形成了研究热声热机的热点.

热声微热力学循环为处于声场和温度场作用下的流相工质，由许多微团组成，通过和与之相接触的固相工质（壁管）发生横向热交换，完成热力循环.近年来阚绪献等人通过对热声微热力学循环的研究，导出了热声热机微热力学循环中经济性能的优化关系式［6－7］，Hussein Chaitou等人则用粒子群最优化方法，优化了热声热机效率［8］.从这些研究工作的结果中可以得到，热声热机的效率与声功率之间的影响关系曲线是封闭曲线，直观地表明了效率与输出声功率之间的关系：在得到最高输出声功率的同时， 效率并非最大，并且随着效率的继续升高，输出声功率可能越来越小.在设计实际的热声热机时，需要获得两者之间的最优关系，当获得高的输出声功率的同时也能获得高的效率.近几年，Hussein Chaitou等人提出了以ηex×Δ〈W〉为目标函数，寻求实际热声热机效率与输出声功率的最佳值［8］.文献［9］中推导出了热声热机微热力学循环在仅有传热损失时效率与输出声功率之间的优化关系

本文中以（1）式为目标函数，其中ηex为热声热机效率，P为输出声功率，在文献［9］的基础上运用有限时间热力学方法，并考虑不可逆程度因子和热漏系数，研究实际热声热机效率与输出声功率关系的最佳值.

1 循环描述与分析

在热声热机中，气体微团进行声振荡，向高温端运动时，气体压力增大，体积收缩，温度升高；向低温端运动时，气体压力减小，体积膨胀，温度降低，其微热力学循环过程如图1所示.根据文献［6－7］，设T0为气体微团在平衡位置处的平均温度，ζm为气体微团位移振荡的幅值，Tm为气体微团温度振荡的幅值，T2为气体微团在绝热压缩过程中的温度振荡值，T4为气体微团在绝热膨胀过程中的温度振荡值，dTm／dx为纵向平均温度梯度.循环模型T－S图如图2所示，气体微团在进行热力循环过程中各个状态点的温度分别T′1＝T0－Tm、T′2＝T0＋T2、T′3＝T0＋Tm、T′4＝T0－T4，与之相接触的壁温分别为T0－ζm dTm／dx、T0＋ζmdTm／dx.若微团与固相工质的换热满足牛顿线性导热规律，则定压吸热过程2－3中，气体微团从固相工质的吸热量大小为：

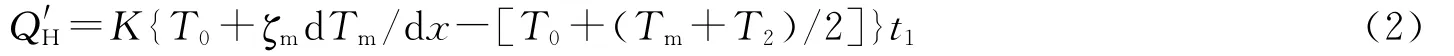
式中Q′H为循环的吸热量，K为热导率，T0＋（Tm＋T2）／2是过程2－3的平均温度，t1是过程2－3所经历的时间，（2）式也可写为：

式中B＝ζmdTm／dx－Tm／2.

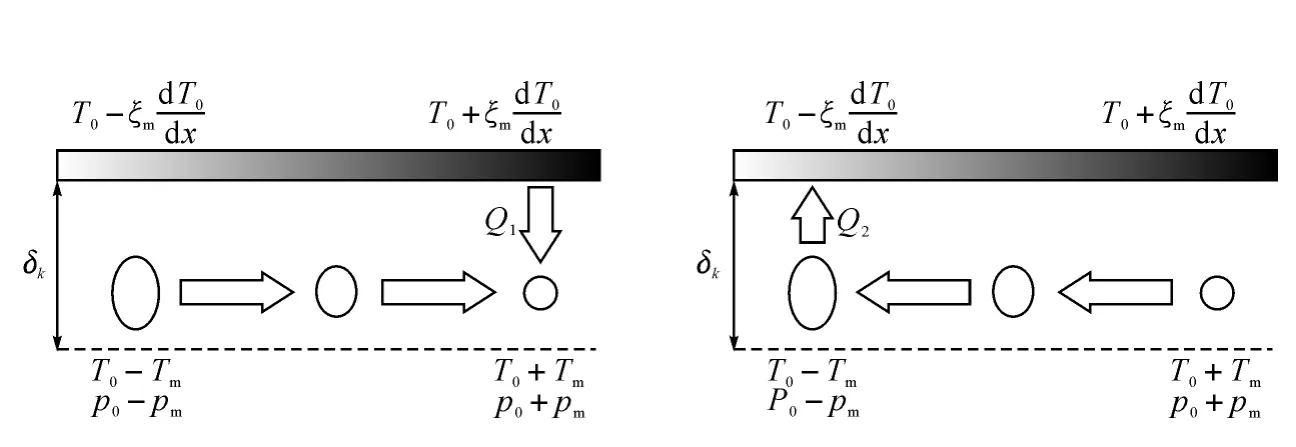
图1 热声热机微热力学循环中微团的热力学过程

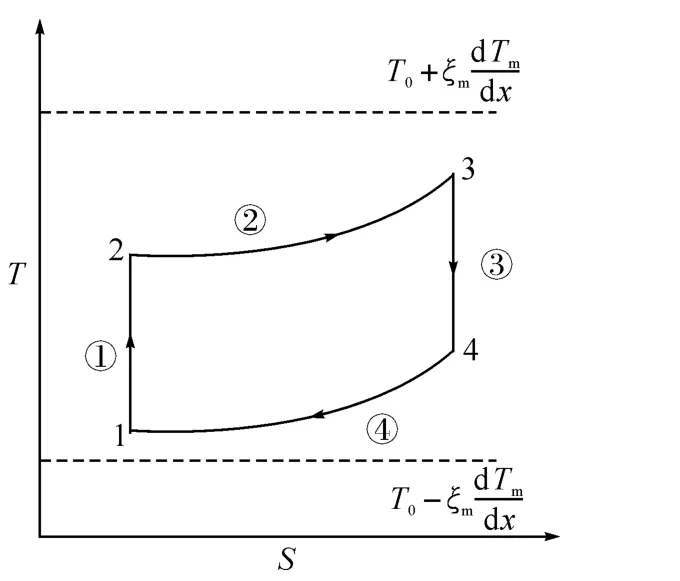
图2 循环模型

设ρ0为流相工质的平均密度，Cp为流相工质的平均定压比热容，则由工质的热力性质可得循环的吸热量大小为：

同理，亦可求得过程4－1中，气体微团向固相工质的放热量大小为：

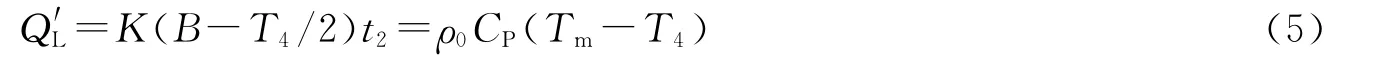
由于在实际热声热机中，存在许多不可逆性，这些不可逆性直接影响了热声热机的效率和输出声功率.用不可逆程度因子φ和热漏量Qi分别表征热声热机中的内、外不可逆性［10－12］，可求得定压过程2－3和4－1中，气体微团对固相工质的实际吸热量QH与放热量QL分别为：

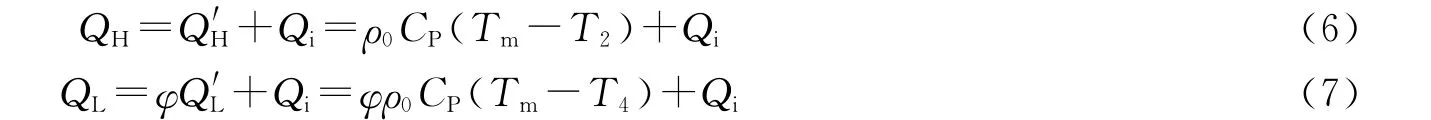
从而可求得定压过程2－3和4－1所历经时间分别为：

相比定压过程2－3和4－1，绝热过程1－2和3－4经历时间较短，可以忽略不计，则循环周期：

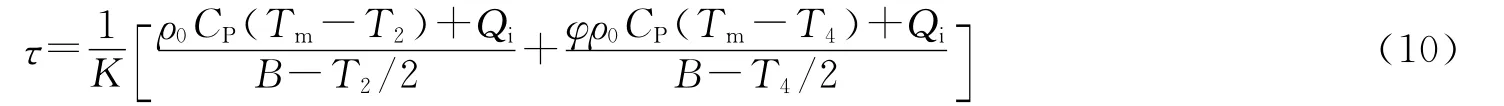
根据文献［6］，包含高阶小量有：

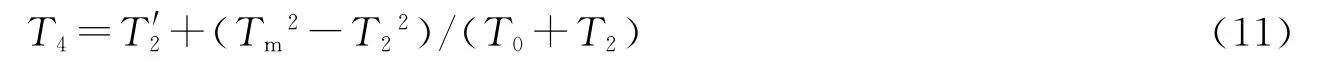
将（11）式代入（10）式中可得：

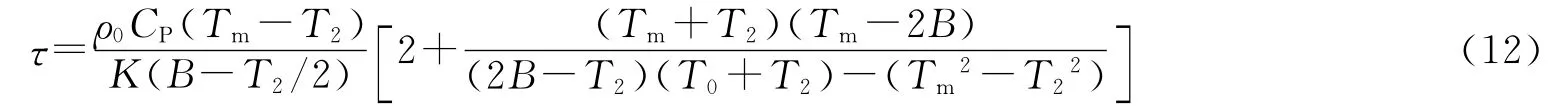
联立（6—7）式和（12）式，可得循环的声功率为：

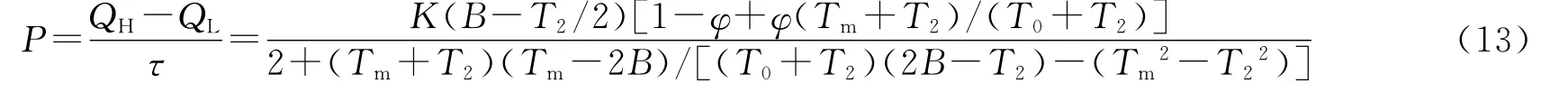
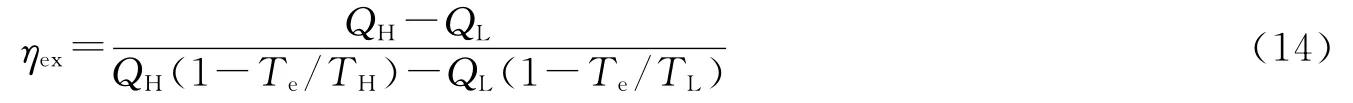
将（6—7）式代入（14）式中可得：

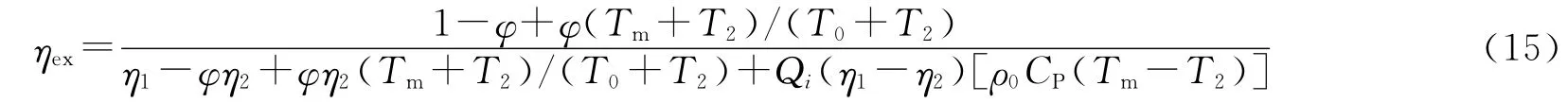
其中Te是环境温度，η1＝1－Te／（T0＋ζmdTm／dx），η2＝1－Te／（T0－ζmdTm／dx）是卡诺系数.

将式（13）式、（15）式代入（1）式可得：

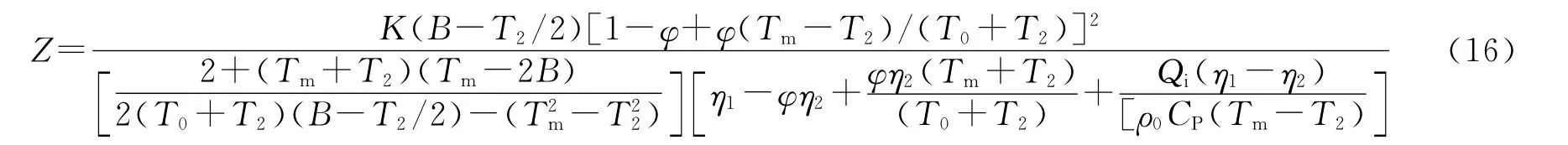
其中令Qi＝q＊τ，q为热漏系数，由（13）式、（15—16）式可以看出，函数Z与工质温度T2存在极值.令dZ／dT2＝0即可以求得最大值Zmax相应的最佳温度Topt，进而求得在此最佳温度Topt下的最佳输出声功率P及其所对应的最佳效率ηex.

2 数值算例

计算时取：Te＝300K、T0＝550K、K＝1 120W／K、Tm＝50K、ζm＝0.003，纵向平均温度梯度取dTm／dx＝15 000K／m，不可逆程度因子φ分别取值1.05、1.10、1.15，热漏系数q分别取1.5KW、2.0KW、2.5KW.设T2为变量且取值范围为［－50，50］，代入以上各式计算，则可得到如下各图所示的关系曲线.

图3是不同的不可逆程度因子φ时，实际热声热机微热力学循环的效率ηex与输出声功率P的关系曲线.从图中可以看出，ηex－P关系曲线呈扭叶型，与内可逆热声热机微热力学循环的抛物线［9］相比较，该曲线形状有很大的改变.通过对实际热声热机微热力学循环的效率ηex与输出声功率P的关系式分析得出，ηex－P曲线形状改变的原因是，在理想情况下的内可逆热声热机微热力学循环中，不考虑热漏量的影响，曲线为抛物线；然而在实际热声热机微热力学循环中，由于热漏量的存在对效率ηex影响很大，从而影响了P－ηex曲线的形状，使其由抛物线改变成为扭叶型.从图中还可以得到不可逆程度因子φ对此关系曲线的扭叶型有很大的影响：随着不可逆程度因子φ的增加，实际热声热机微热力学循环的效率ηex与输出声功率P之间的扭叶型曲线逐渐收缩变小，即相对应的微热力学循环的效率ηex与输出声功率P也在逐渐变小.

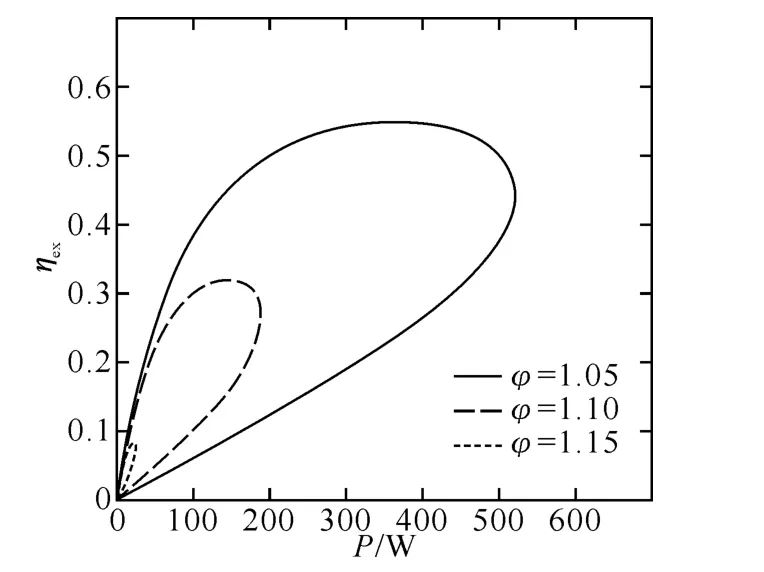
图3 不同的不可逆程度因子φ时，效率ηex与输出声功率P的关系曲线

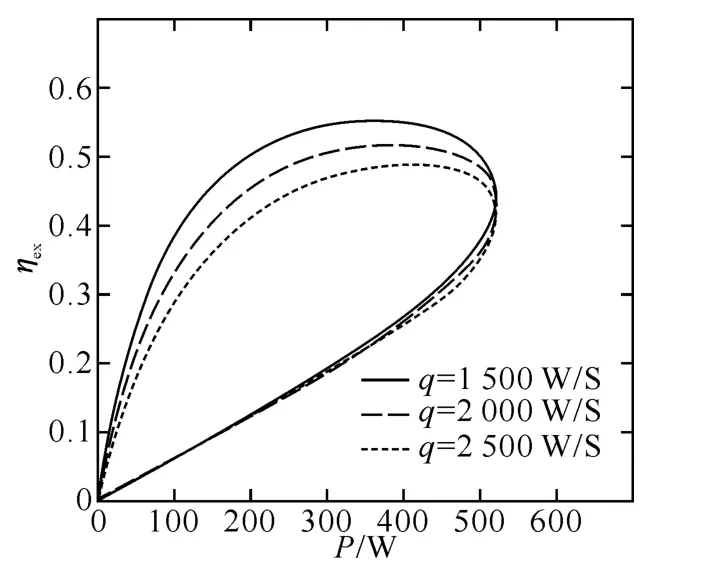
图4 不同的热漏率q时，?效率ηex与输出声功率P的关系曲线

图5是不同的不可逆程度因子φ时，实际热声热机微热力学循环的目标函数值Z与振荡温度值T2的关系曲线.从图中可以看出，关系曲线呈抛物线形，在所规定的温度振荡值T2取值范围内，随着振荡温度T2的增大，实际热声热机微热力学循环的目标函数值Z先逐渐升高，随后逐渐递减直至为零，可知存在一最大目标函数值Zmax及其对应的最佳温度振荡值Topt，当T2＝Topt时，实际热声热机在获得高效率ηex的同时也能获得高的输出声功率P，此最佳温度振荡值Topt所对应的实际热声热机微热力学循环的效率ηex与输出声功率P即为最优.从图中还可以看出，随着不可逆程度因子φ的增加，该循环最大的目标函数值Zmax逐渐减小，其相对应的最佳振荡温度值Topt逐渐升高.

图6是不同的热漏率q时，实际热声热机微热力学循环的目标函数值Z与振荡温度值T2的关系曲线.从图中可以看出，随着热漏率q的升高，该循环最大的目标函数值Zmax逐渐减小，但最大的目标函数值Zmax相对应的振荡温度值Topt几乎不变，即在其他条件一定时，无论热漏率q如何变化，该循环的最大的目标函数值Zmax所对应的振荡温度值Topt基本不变.

图5 不同的不可逆程度因子φ时，目标函数值Z与振荡温度值T2的关系曲线

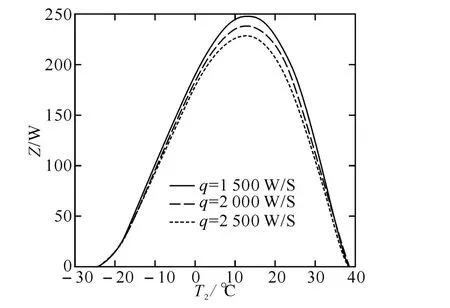
图6 不同的热漏率q时，目标函数值Z与振荡温度值T2的关系曲线

3 结论

本文中通过实际热声热机微热力学循环的模型，用有限时间热力学的方法导出了循环的效率ηex与输出声功率P最优特性关系，并由数值计算得到了不可逆程度因子φ和热漏系数q对效率ηex与输出声功率P的关系曲线、循环的目标函数值Zmax与温度振荡值T2的关系曲线的影响.结果表明：实际热声热机微热力学循环中存在一最佳温度振荡值，使循环在得到高的效率ηex的同时得到高输出功率P，最佳温度振荡值Topt随不可逆程度因子φ的增大而升高，而热漏系数q对最佳温度振荡值Topt影响不大.

［1］P H Ceperly.Gain and efficiency of a traveling wave heat engine［J］.Acoust Soc Am，1982，7（3）：1239－1243.

［2］Yazaki T，Iwata A，Mackawa T，et al.Traveling wave thermoacoustic engine in a looped tube［J］.Physical Review Letters，1998，81（15）：3128－3131.

［3］Back S，Swift G W.A thermoacoustic stirling wave heat engine［J］.Nature，1999，399：335－338.

［4］吴锋，李青，郭方中，等.热声理论的研究进展［J］.武汉工程大学学报，2012，34（1）：1－6.

［5］Wu Feng，Li Qing，Guo Fangzhong，et al.Advance in thermoacoustic theory［J］.J Wuhan Inst Tech，2012，34（1）：1－6.

［6］阚绪献，吴锋.热声制冷机微热力学循环的经济性能优化［J］.低温与超导，2008，36（10）：1－4.

［7］Kan Xuxian，Wu Feng.Finite time exergoeconomic performance of a thermoacoustic refrigeration micro－cycle［J］.Cryo ＆Supercond，2008，36（10）：1－4.

［8］Hussein Chaitou，Philippe Nika.Exergetic optimization of a thermoacoustic engine using the particle swarm optimization method［J］.Energy Conversion and Management，2012，55：71－80.

［9］Lin Jie，Wu Feng，Fei Jinhua，et al.The exergy efficiency and output acoustic power performance optimization of the thermoacoustic engine micro－cycle［J］.Advanced Materials Research Vols，2013，712－715：1609－1613.

［10］Chen L，Wu C，Sun F.Effect of heat transfer law on finite time exergoeconomic performance of a carnot refrigerator［J］.Exergy，An Int J，2001，1（4）：295－302.

［11］Wu F，Chen L，Wu S，et al.Optimum performance of irreversible stirling engine with imperfect regeneration［J］.Energy Convers Mgmt，1998，39（8）：727－732.

［12］Kan X，Chen L，Sun F，et al.Finite time exergoeconomic performance optimization of a thermoacoustic heat engine［J］.International Journal of Energy and Environment，2011，2（1）：85－98.