基于数学形态学的去方块效应法

汪晓波，刘斌

（湖北大学计算机与信息工程学院，湖北武汉430062）

0 引言

图像的边缘包含了大量信息，而基于多分辨的奇异值分解图像融合［1－2］后的图像的边缘会出现方块效应，这将导致融合的分辨率不高，融合图像质量下降.Kakarala R［1］等人将多分辨奇异值分解应用于一维信号和二维图像，在得到低频和高频部分的同时，也达到了最佳去相关分解和线性计算复杂性，并能保证完全重构.近年来，这种方法在信号与图像处理中得到广泛应用，如Ashino R［2］等人将其应用去数字图像压缩，并结合小波变换实现二重小波－奇异值分解方法，既能实现最佳去相关分解，又能保证分解时时频共存，若使用长的小波滤波器，得到的图像中方块效应比单独的SVD更弱.

1964年法国的Matheron和Serra在积分几何的研究成果上，将数学形态学引入图像处理领域，并在理论上日趋完备化.近年来，为了更灵活更合理地使用数学形态学方法，Gasteratos等将模糊集合理论与软数学形态学结合得到模糊软数学形态学，可以根据图像的拓扑结构，合理选择模糊集合运算算子及结构元素核心、软边界的定义域，并通过改变匹配参数来调整输出结果.数学形态学［3］是建立在严格数学理论基础上的学科，其基本思想是用具有一定形态的结构元素度量和提取图像中的对应形状以达到图像分析和识别的目的，可用于特征提取、边缘检测、图像分割、图像恢复与重构等.

目前也有很多去方块效应的方法，但大多针对的是单纯的有方块效应的图像，或者是DCT（离散余弦变换）［4］后的方块效应的图像，它们不具有普遍性，不能简单用于小波变换和MSVD融合后有方块效应的图像.笔者经过多次试验发现：基于小波变换的去方块效应法［5］对于这种融合后的图像方块效应计算量大，效果不明显；而基于形态学的图像融合算法［6－7］也不能避免出现多分辨奇异值分解融重构后的方块效应.考虑到方块效应多出现在边缘，可以用基于边缘检测的去方块效应法［8］在DCT域上逐行进行平滑处理，但这通常会导致过分平滑，而且大大降低了运算速度.

为了消除融合后的方块效应，增强图像的质量，提出了基于形态学边缘检测［9］的融合后处理方法.对两幅待融合图像进行边缘检测，将边缘图后的像融合作为原融合结果图像的边缘，再由边缘检测梯度逆变换得到去除方块效应的的结果图像.结果显示图像的清晰度和空间频率都有很大提高，且具有较好的保边缘性.

1 灰度形态学基础运算

灰度形态学处理［10］的对象和结构元素都是灰度函数，可以充分考虑图像的灰度信息，更完整地描述图像的基本形状特性.腐蚀和膨胀是数学形态学的两种基本运算，由这两种基本运算可以组成多种复合运算，产生不同的形态学实用算法.在这些运算中结构元素的选取非常重要，它可以调整图像特征变换的几何结构，有针对性地选择结构元素和运算方式，对某一特定目标进行减弱或加强.对边缘进行处理时要考虑图像边缘的几个重要特征：边缘处像素灰度值变化不连续；边缘处灰度值具有方向性；边缘两侧具有不同的纹理特征.

1.1 膨胀和腐蚀 设f（x，y）代表输入图像，b（i，j）代表结构元素，用结构元素b对输入图像f进行灰度腐蚀，定义为：

用结构元b对输入图像f进行灰度膨胀定义为：

其中Df和Db分别是函数f和b的定义域，位移参数必须包含在函数的定义域内.

可见，膨胀运算时在有结构元素确定的邻域内选取f＋b的最大值，是局部最大值滤波.如果结构元素的值为正，膨胀运算后图像的灰度要变大.这种使灰度值变大的作用对于灰度变化很大的点（图像边缘）就越为突出.因此，可以利用膨胀运算对边缘处作用明显，而对非边缘处的作用较微弱的这一特点，求出膨胀运算后图像与原图像的差异，则可突出图像边缘，进行边缘提取.而腐蚀运算是在由结构元素确定的邻域内选取f－b的最小值，是局部最小值滤波，它使整幅图像灰度值降低，而且也只是对边缘处的作用非常明显.若将原图像与经过腐蚀运算的图像相减，则可以得出图像边缘.

1.2 基本形态学边缘检测算子 根据上述形态学基本运算对图像边缘的增强作用，可以构造以下几种基本形态学边缘检测算子，也叫形态学梯度：

膨胀型：g1＝f⊕b－f，

腐蚀型：g2＝f－fΘb，

膨胀腐蚀型：g3＝f⊕b－fΘb，

形态学边缘检测算子是一种非线性差分算子，而且其检测出的边缘与结构元素有关.这些算子实现简单，在实际中有一定的应用.这3种算子可以分别提取图像的外边缘、内边缘和骑跨在实际欧式边界上的边缘，但对噪声都很敏感，适用于噪声较小的图像.

本文中采用3×3单位矩阵作为结构元素，选择膨胀腐蚀型边缘梯度算子，对MSVD融合后的图像进行一系列处理后得到均匀性较好的图像，得到的最终图像的方块效应有所减弱甚至消失，得到的图像在视觉上更容易使人接受.

2 形态学去方块效应法

为验证去方块效应算法的性能，使用MSVD多聚焦融合后的图像进行实验.选取多聚焦图像clock图像，实验步骤如下：

Step1：对多聚焦图像进行MSVD融合，得到融合结果图像F；

Step2：对待融合的两幅多聚焦图像I、J进行边缘检测，根据绝对值最大规则融合边缘得到边缘融合图像E选择的结构元素se，求I、J的边缘梯度图像：

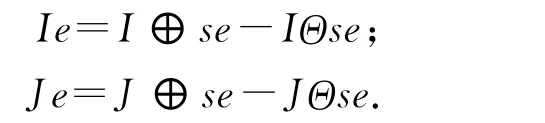
Step3：把边缘融合图像E作为原融合结果图像的边缘，再进行边缘梯度逆变换，得到边缘加强的图像Fe，操作为：

经过上述操作后，图像的清晰度有所提升，空间频率有很大提高，且具有较好的保边缘性，视觉效果也更佳.

3 实验及结果评价

为验证方法的有效性，实验采用上述图像在MATLAB 7.0上实现上述算法，并且用空间分辨率和清晰度作为实验结果的客观评价指标，主观上采用放大处理，对比去方块效应前后的图像变化，如图1～2所示：图1为两幅待融合的图像，大小为512×512，图1（a）为聚焦左边的图像，图1（b）为聚焦右边的图像.图2（a）为使用MSVD融合得到的融合结果图像，图2（b）为使用本文中建议的方法得到的去方块效应后的图像.

图1 待融合的clock图像

图2 clock图像融合后处理图像比较

将图2中的（a）和（b）图像进行观察对比可知，本文中方法有效地消除了融合后图像的方块效应，边缘处的锯齿状基本已经消失，视觉效果更加清晰，比如时钟上的英文字母字和小时钟上的数字都比原来清晰很多.

对上述图像进行客观评价时采用清晰度、空间分辨率和保边缘度（QABF）指标，如表1所示.评价结果表明经过本文中方法的处理，方块效应有明显改善，图像的清晰度显著增强，空间频率有很大提高，且图像更好地保持了边缘特性.

表1 实验结果评价数据

4 结论

提出了一种基于数学形态学去方块效应的新方法，在基于多分辨奇异值分解的图像融合基础上，对图像进行形态学边缘梯度检测，通过加强边缘信息，有效地去除了方块效应.提出的方法简单有效，去除方块效应后的图像更加清晰，有较好的视觉效果.从客观性能指标看，该方法保持清晰度和空间频率信息比有方块效应的图像要高出很多，且更好地保持了边缘特性.

利用本文中建议的方法对其他融合后出现方块效应的情况做了相同的后处理，如多光谱图像融合，可见光图像和红外图像融合，也得到了与上述结论相同的结果，该方法确实有广泛的适用范围.

［1］Kakarala R，Ogunbona P O，Member S.Signal analysis using a multiresolution form of the singular value decomposition［J］.IEEE，2001，10（5）：724－735.

［2］Ashin R，Morimoto A，Vaillancourt R.Image compression with multiresolution singular value decomposition and other methods［J］.Mathematical and Computer Modelling，2005，41（6／7）：773－790.

［3］杨晖，张继武.数学形态学在图像边缘检测中的应用研究［J］.辽宁大学学报，2005，32（1）：50－53.

［4］周昌雄，于盛林.基于总体方差最小消去DCT的方块效应［J］.电子科技大学学报，2005，5（34）：661－664.

［5］陈琍，朱秋煜，杜干.基于小波变换的方块效应去除法［J］.微计算机信息，2007，23（8）：283－284，267.

［6］刘伟军，孙兴波.基于形态学的图像融合算法［J］.四川理工学院学报：自然科学版，2006，19（6）：21－23.

［7］夏开建，姚宇峰，钟珊.基于形态学小波变换的图像融合算法［J］.计算机工程与应用，2010，35（19）：224－226.

［8］石敏，易清明，刘金梅.一种基于边缘检测的去方块效应算法［J］.计算机工程与应用，2007，43（8）：27－28.

［9］魏军伟，方敏.基于最大熵和形态学的边缘检测［J］.计算机工程与应用，2007，43（21）：70－72.

［10］王焱，邹步，彭慧玲.基于形态学的边缘检测研究［J］.现代制造工程，2011（12）：87－90.