一种基于小波变换的红外偏振融合算法

岳 振,李范鸣

(1. 中国科学院 上海技术物理研究所，上海 200083；2. 中国科学院 红外探测与成像技术重点实验室，上海 200083)

引言

因为不同目标的表面材料、表面粗糙程度和理化特征等不同，红外系统从场景中获得的反射辐射和自发辐射会表现出不同的偏振特性，因此偏振成像可以反映目标对入射光偏振特性的影响[1]。人造目标和自然目标的偏振特性差别较大，这可以增大目标与背景的对比度，从而提高目标检测的效率[2]。偏振成像增加了偏振信息，并且也保留了原有的辐射强度信息。偏振度图像可以较好地抑制背景噪声，对目标边缘信息比较敏感，但视觉效果较差[3]，红外辐射强度图像包含了更多背景信息[4]。因此，根据偏振度图像和辐射强度图像的特点，可以将红外辐射强度图像与偏振度图像融合到一幅图像，增强目标和背景的对比度，提高目标探测的效率[5]。基于小波变换的图像融合方法，可在不同频率分量、不同分解层、不同方向采用不同的融合规则及融合算子进行处理。此外，同一分解层上的不同局部区域也可采用不同的融合算子[6]。文中提出一种基于小波变换的红外偏振图像融合算法，并将其应用于红外辐射强度图像和偏振度图像融合。实验结果表明，这种方法增加了图像的对比度和清晰度。

1 中波红外线偏振图像的获取

偏振是各种矢量波共有的一种性质,经常使用斯托克斯矢量描述法来描述偏振态[7]。Stokes描述法由I，Q，U，V4个参量来描述[8]。线偏振斯托克斯矢量测量指的是红外辐射中不包含圆偏振分量或圆偏振分量相对极小的情况下进行的偏振测量。线偏振测量需要用线偏振片进行起偏，假设线偏振片的输入信号为Sin=[IQUV]T，输出信号为Sout=[I′Q′U′V′]T，β为偏振器件透射方向与参考方向之间的夹角。要得到目标偏振度成像，需要4幅在不同偏振角度下的图像来计算所需要的斯托克斯矢量[9]。取β分别为0°、45°、90°和135°，可以得到：

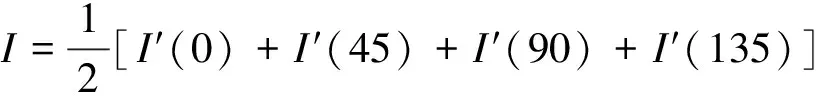
(1)

这样便求解得到了入射辐射斯托克斯矢量的前3个参数。线偏振度的公式由此可以写为

(2)

(1)式和(2)式便是进行红外偏振成像系统设计的主要依据。实际测量时，通过旋转线偏振片，依次采集0°、45°、90°和135°方向的图像数据，得到对应的辐射强度I′(0)、I′(45)、I′(90)和I′(135)，将其代入(1)式，求出斯托克斯矢量的前3个参数I、Q和U，然后再依次代入(2)式，便可以得到线偏振度LDoP，进而成像显示[9]。

2 基于小波变换的红外偏振图像融合算法

本文采用小波变换对红外辐射强度图像和偏振度图像进行融合。小波变换可将源图像进行多尺度分解[11]，针对其不同尺度的小波系数，分别采用不同的融合算子进行融合处理，然后通过小波逆变换进行图像重构，可将红外辐射强度图像的低频特征和偏振信息图像的高频特征融合在一起，从而使融合后图像的信息量增大。

2.1 基于小波变换的图像分解

首先对图像进行小波分解，得到各尺度小波系数。最高尺度J的近似系数Wφ(J,m,n)取函数本身，即Wφ(J,m,n)=f(m,n)。对尺度J-i，其中i=1,…,c，c为小波分解层数，按照图1所示进行分解，具体步骤如下：

图1 基于小波变换的图像分解方法Fig.1 Image decomposition method based on wavelet transform

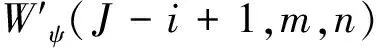
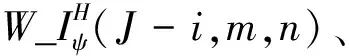
2.2 对各尺度小波系数进行融合

红外辐射强度图像包含了更多背景和细节信息，多表现为低频特征。对红外辐射强度图像和偏振度图像的尺度J-c近似系数，它们都是对源图像的近似，包含有源图像的低频特征。因为红外辐射强度图像的尺度J-c近似包含了更多的低频特征，所以本文将红外辐射强度图像的尺度J-c近似系数直接作为尺度J-c的融合近似系数。对红外辐射强度图像和偏振度图像的尺度J-i细节系数，i=1,…,c，它们包含更多的高频特征，分别以局部邻域平均梯度为判据，进行图像融合，得到尺度J-i融合细节系数。其具体方法步骤如下：

1)对于尺度J-c融合近似系数，直接采用红外辐射强度图像的尺度J-c近似系数:

W_Rφ(J-c,m,n)=W_Iφ(J-c,m,n)

(3)

式中：W_Iφ(J-c,m,n)为红外辐射强度图像尺度J-c近似系数在点(m,n)处的值；W_Rφ(J-c,m,n)为尺度J-c融合近似系数在点(m,n)处的值；

2)对于尺度J-i细节系数，i=1,…,c，以局部邻域平均梯度为判据，进行细节系数融合，对任一点(m,n)，计算以此点为中心的局部邻域的平均梯度值，平均梯度H计算公式如下：

(4)

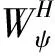
(5)

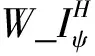
2.3 基于各尺度融合后的小波系数进行图像重构

得到各尺度融合后的小波系数，需要对各尺度融合后的小波系数进行重构，得到最终的融合图像图2，具体步骤如下：

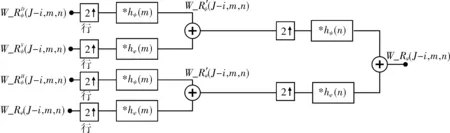
图2 基于小波变换的图像重构Fig.2 Image reconstruction based on wavelet transform

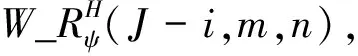
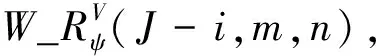
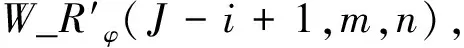
4) 重复步骤1)～3)，最终得到W_Rφ(J-i+1,m,n)，即为最终的融合图像F(m,n)。

3 实验结果和评价

3.1 融合评价指标

1)标准差

(6)

在某种程度上，标准差也可用来评价图像反差的大小：标准差越大，图像的灰度分布越分散，图像的反差也越大，可看出的信息也越多。

2)信息熵

图像的信息熵是衡量图像所含信息丰富程度的一种重要指标，熵值的大小反映了图像所含平均信息量的多少，其定义为

(7)

式中pi为灰度级i的分布概率，其范围是[0,1,…,L-1]。融合图像的熵值反映了其包含信息量的多少，熵值越大说明融合图像的信息量越丰富，融合效果越好。

3)梯度均值

梯度均值[1]是一个反应图像细节对比度和纹理特征变化的指数，其定义如下：

(8)

g值越大，图像的区分度越大，图像就越清晰，说明融合效果越好。

3.2 实验结果

基于小波变换的红外偏振图像的融合方法可以根据需要分解为c层，经测试，图5为对居民楼的红外辐射强度图像、偏振度图像以及采用本文融合算法(c取2、3、4、5、6)的融合图像。其中图像的大小均为256像素×256像素。融合后图像在保留了红外辐射强度图像的背景信息的同时，图像中的空调、晾衣架、窗户的金属框都变得更加清晰。

图3(c)是c取2时的融合图像，此时图像的背景信息很清晰，偏振度图像中的细节信息并没有很清楚地显示出来，这是因为根据本算法，融合后J-c级近似系数直接采用红外辐射强度图像的J-c级近似系数。所以当分层较小时，直接融合的辐射强度图像的信息量较大，而偏振度信息量较少。当c取3时，背景信息开始减弱，但细节信息开始增强。当c取4、5、6时，背景信息进一步减弱，细节信息进一步增强。所以算法可以自由调节分层数c，从而在突出背景或者细节之间进行平衡。

图3 融合图像效果Fig.3 Fusion image results

根据中图像评价指标，融合前后图像的评估结果见表1，表1列出了红外辐射强度图像和偏振度图像以及融合后图像的标准差、信息熵、梯度均值等评价指标值，数据显示，融合后的图像在3项指标中均得到了提升。当c=3时，相对于辐射强度图像，融合图像的梯度均值提高了112%，相对于偏振度图像，融合图像的标准差提高了151%，信息熵提高了38%。

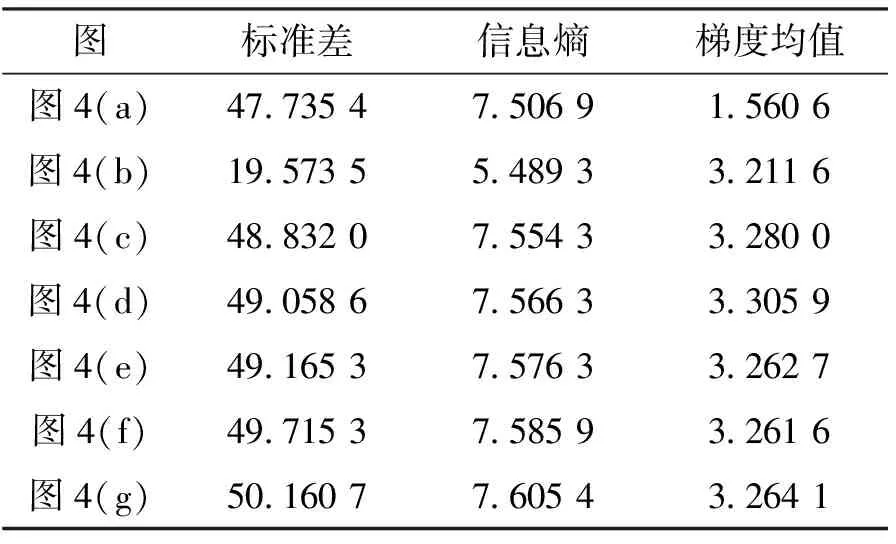
表1 图像评估结果Table 1 Image evaluation results

4 总结

本文简要地介绍了红外偏振成像的基本理论，详细描述了一种基于小波变换的红外偏振图像融合算法，引入邻域平均梯度为判据进行图像融合。实验结果表明：采用此算法，融合后的图像视觉效果更好，一些边缘信息得到明显突出。通过对融合前后图像的标准差、信息熵、梯度均值等量化指标进行对比，可以看出融合后图像的各项指标均得到明显提升。当小波分解层数为3时，相对于辐射强度图像，融合图像的梯度均值提高了112%，相对于偏振度图像，融合图像的标准差提高了151%，信息熵提高了38%。

[1] YANG Wei , GU Guo-hua , CHEN Qian , et al. A wavelet-based adaptive fusion algorithm of infrared polarization imaging[J]. SPIE, 2011, 8193:1-9.

[2] LIU Xiao, WANG Feng, Xue Mo-gen. The study of camouflage target detection based on polarization characteristics[J]. Optical Technique, 2008,34(5):787-790.

[3] MEDKOUR T,WALDEN A T. Statistical properties of the estimated degree of polarization[J]. IEEE Transactions on Signal Processing, 2008, 56(1): 408-414.

[4] LIU Xiao, WANG Feng. The research of polarization image fusion method based on modulation in multi-scale space[J]. SPIE，2011，8194:1-9.

[5] YEMELYANOV K M, LIN S-S, PUEH E N, Jr,et al. Adaptive algorithms for two-channel polarization sensing under various polarization statistics with nonuniform distributions[J]. Optical Engineering，1981，20(1) : 14-18．

[6] 王海晖,彭嘉雄,吴巍．基于小波包变换的遥感图像融合[J]．中国图像图形学报，2002,7(9):932-937．

WANG Hai-hui, PENG Jia-xiong, WU Wei. Remote sensing image fusion based on wavelet packet transform[J]. Chinese journal of image and graphics, 2002,7(9):932-937．(in Chinese with an English abstract)

[7] WALRAVEN R. Polarization imagery[J]. Optical Engineering，1981，20(1): 14-18．

[8] WOLFF L B, ANDREOU A． Polarization camera sensors[J]． Image and Vision Computing，1995，13(6) : 497-510．

[9] 李范鸣,牛继勇,马利祥.基于红外偏振特性的空间目标探测可行性探讨[J].应用光学，2013,34(4): 653-657.

LI Fan-ming, NIU Ji-yong, Ma Li-xiang. Feasibility analysis of space target detection based on infrared polarization properties[J]. Journal of Applied Optics, 2013, 34(4): 653-657.(in Chinese with an English abstract)

[10] 马利祥.红外偏振成像系统关键技术研究[D].上海：中科院上海技术物理研究所，2013.

MA Li-xiang. Research on key technologies for infrared polarimetric imaging system[D].Shanghai: A Dissertation of Shanghai Institute of Technical Physics, Chinese Academy of Sciences,2013.(in Chinese)

[11] PRASAD L, IYENGAR S S. Wavelet an analysis with application to image processing [M]. New York: CRC Press, 1997.