基于博奇编码离轴全息方法的研究
2014-03-27许忠保邬文俊周胜飞王心怡
陈 林,许忠保,2,邬文俊,2,周胜飞,王心怡
(1.湖北工业大学 机械工程学院,湖北 武汉 430068;2.湖北省现代制造质量工程重点实验室,湖北 武汉430068)
引言
随着数字计算机与计算机技术的迅猛发展,人们广泛地使用计算机去模拟、运算、处理各种光学过程。计算机产生全息图已有近50年的历史,与传统的光学全息相比较,计算全息具有简单、灵活、方便的特点[1],已广泛应用于空间滤波[2-4]、三维显示[5]、全息干涉、数字水印[6-7]等领域。历经数十年的研究发展,计算全息的编码方式产生了罗曼编码[8]、博奇编码、黄氏编码、李威汉编码和迭代算法等多种技术[9-10]。
原始像与共轭像的混叠现象严重影响计算全息的再现像质,通常消除再现像混叠现象的方法是加入倾斜参考光与原物光波干涉叠加,并计算出最小倾斜角来使原始像与共轭像完全分离。本文根据光学离轴全息和博奇编码理论,研究了一种基于博奇编码制作全息图的方法,将原物抽样点嵌入比原物大的全零矩阵中代替载频参数的计算过程,并建立了一套全息显示系统用于实验验证。该方法消除了原始像与共轭像的混叠现象,并可以通过控制全零矩阵的大小来控制再现时原始像与共轭像的分离程度。
1 基本原理
1.1 光学离轴全息原理
为了消除同轴全息图中孪生像的干扰,在制作全息图时加入倾角为θ的倾斜参考光,设传播到记录介质平面的物光波和平面参考光波分别为
f(x,y)=A(x,y)exp[jφ(x,y)]
R(x,y)=Rexp(j2παx)
式中:A(x,y)、R分别表示物光波与参考光波的振幅;jφ(x,y)、j2παx分别是物光波与参考光波的相位;参考光波的空间频率α=sinθ/λ,λ为参考光波波长。物光波与平面参考光波在记录平面发生干涉,得到记录平面上的总光强分布为
h(x,y)= |f(x,y)+R(x,y)|2=
R2+|f(x,y)|2+Rf(x,y)exp[j2πx]+Rf*(x,y)exp[-j2παx]=
R2+|A(x,y)|2+2RA(x,y)cos[2παx-φ(x,y)]
(1)
当参考光波入射到全息面上时,在像面上会出现分离的原始像和共轭像。并且参考光和全息图之间的夹角θ越大,则再现的原始像和共轭像与原照明光波分的越开。
1.2 博奇型计算全息编码原理
光学离轴全息图的空间频率分布如图1所示,物体在频域中的带宽为Bx和By。图1中,μ=±α的2个矩形代表物波的频率成分,中间的大矩形是|f(x,y)|2的自相关频率成分以及基波的脉冲响应函数R2,为了避免在频域中这些分量之间的重叠,载频α≥(2Bx+Bx)/2=1.5Bx。h(x,y)在二维方向的最高频率分别为2Bx、By,则由抽样定理可知对其抽样的间隔为
(2)
可见,直接用(1)式的全息图透过率函数计算全息图,抽样点数目多,制作起来不方便。

图1 全息图的空频分布图Fig.1 Spatial frequency distribution of hologram
由(1)式可以看出,R2+|f(x,y)|2只对偏置分量有贡献,它使得h(x,y)为实的非负函数,后一项则是提供了物体的全部信息。但由于存在这种形式的偏置,增加了全息图记录时的带宽要求,同时在再现时会出现多余的衍射像。由于计算机具有灵活性的特点,可以加其他形式的偏置分量来达到使其为实的非负函数的目的,由此可降低带宽,减少抽样点数,便于制作及提高再现像质。因此博奇提出加直流偏置K来代替(1)式中R2+|A(x,y)|2,则重新构成的全息函数为
h(x,y)=K+Rf(x,y)exp[j2πx]+
Rf*(x,y)exp[-j2παx]=K+
2RA(x,y)cos[2παx-φ(x,y)]
(3)
规一化|A(x,y)|max=1,R=1,则(3)式变为
h(x,y)=0.5{1+A(x,y)cos[2παx-φ(x,y)]}
(4)
(4)式的第一项是常数,第二项是物波的全部信息,此时全息图的空间频率分布如图2所示。h(x,y)缺少了|A(x,y)|2项,频域中的自相关成分就不再出现,为避免频率平面各分量之间的重叠,载频就只需α=Bx/2。此时,在二维方向的最高频率分别为Bx、By/2,则由抽样定理可知对其抽样的间隔为
(5)
与(2)式比较不难得出,总的抽样点数降低为原来的25%。而且由(4)式可知,全息图再现时的噪声分量只有中间的平面波分量,在滤波的时候会方便很多。
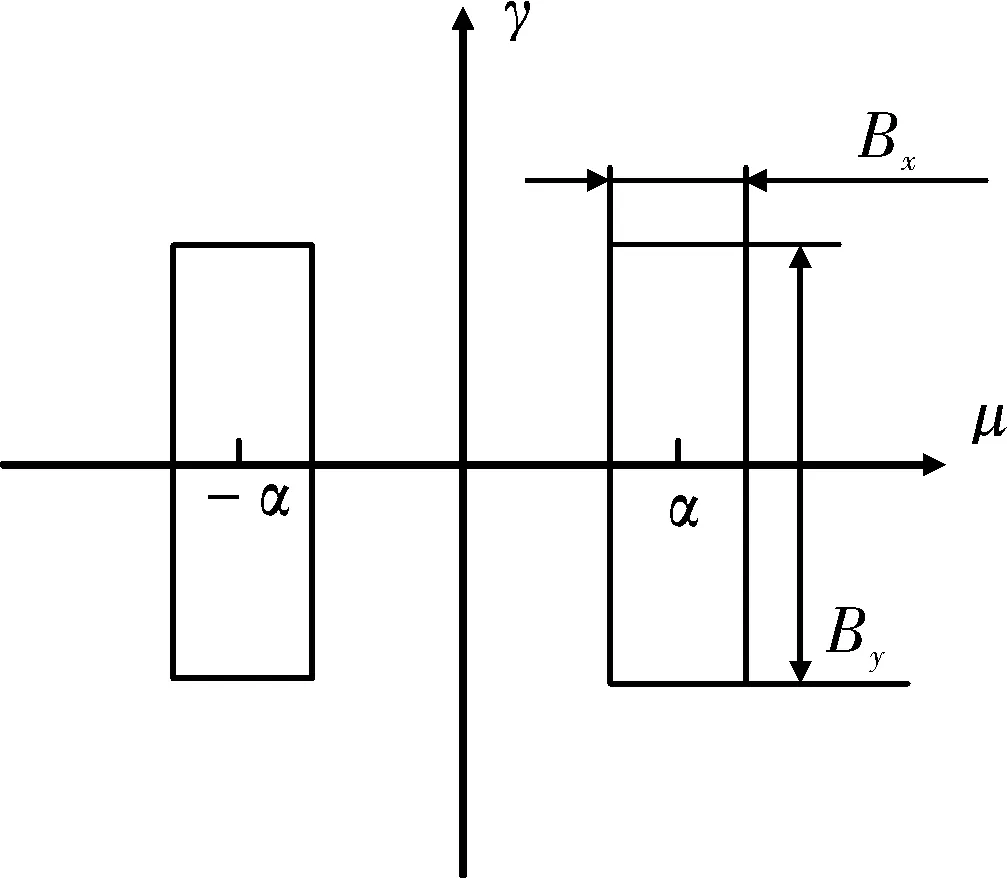
图2 博奇型全息图的空频Fig.2 Spatial frequency distribution of Borg hologram
2 一种改进的博奇编码方法
本文研究了一种改进的博奇编码方式,将原物抽样点f(x,y)镶嵌到比原物更大的全零矩阵中,在不计算载频参数的情况下分离原始像与孪生像,得到新的矩阵f1(x,y):
(6)
对f1(x,y)以博奇编码方式编码后得到全息函数h1(x,y),再对全息函数进行傅里叶逆变换后再现像为
g1(μ,v)=Kδ1(μ,v)+f1(μ-α,v)+
f1(-(μ+α),-v)
(7)
由上式可知3个大小与f1(x,y)相同的矩阵分别为
(8)
(9)
(10)
在矩阵f1(μ-α,v)、f1[-(μ+α),-v]中,与f*(x,y)、f(x,y)对应的元素值为零,故f(x,y)与f*(x,y)不会因(8)式中的三项相加而造成重叠。且控制全零矩阵的大小便可控制再现时原始像与共轭像的分离程度,全零矩阵越大,其分离程度越大。
3 计算全息图的制作与模拟再现
本文通过计算机读入一幅图像,得到一个256×256的矩阵,将此矩阵写入一个比原物大的全零矩阵中并归一化。因为由离散傅里叶变换(discrete Fourier transform,DFT)计算物函数的傅里叶变换谱时,幅值波动范围很大,如在极小值处,计算机绘制的全息图光栅宽度将变为一条细线,缩小后几乎分辨不出,因而产生再现误差,故在进行DFT前给每一个单元乘以单位振幅的随机指数函数,用它来平滑傅里叶变换谱,降低其动态范围。再现时仅仅只有像的强度可被观察到,所以引入的随机指数函数并不影响到强度的变化。这种做法实质上是模仿了光学全息中在物体前放置毛玻璃产生漫反射光线的效应,使物体上各点成为单一的发光点,这样可降低其动态范围,而物体的形状再现时不会发生改变。比较离散傅里叶变换和连续傅里叶变换的定义可知,在做DFT时会在x和y方向上发生平移,按照傅里叶变换的平移定理,必然会在原物函数中引入一个附加相位因子,从而改变原物函数的频谱分布。具体来说,这样会将物频谱的低频成分移到谱平面的边缘,所以为解决上述问题,应用Matlab软件只需在编码前用移谱函数fftshift()将频谱的低频成分移到中心即可。然后利用(4)式得到全息图的数据,通过抽样间隔确定合适的全息图以及抽样单元的大小,最后归一化绘图,便可得到全息图。
本文运用Matlab模拟全息图再现的过程,验证了将原物抽样点镶嵌到不同大小的全零矩阵会得到不同程度的共轭像与原始像的分离,结果如图3所示。
首先,设定载频参数α=0,然后将原物抽样点写入不同大小的全零矩阵当中,由图3不难看出,全零矩阵的大小不同使再现像中原始像与共轭像分离的程度不同。图3(a)表示将原物抽样点写入256×256的全零矩阵中,原始像与共轭像完全重叠;图3(b)表示将原物抽样点写入380×380的全零矩阵中,原始像与共轭像部分重叠;图3(c)表示将原物抽样点写入512×512的全零矩阵中,原始像与共轭像刚好分离;图3(d)表示将原物抽样点写入600×600全零矩阵中,原始像与共轭像的分离较开。由实验结果可知,被写入的全零矩阵越大,共轭像与原始像分的越开。然而,理论上来说,将原物抽样点写入原来灰度图像4倍大小的全零矩阵中,便可以得到清晰的再现像。但由于零级像比±1级像的强度大得多,3个衍射像靠的太近,对零级像进行滤波时,会对再现像的像质造成影响。因此,被写入的全零矩阵最好大于原来灰度图像的4倍。同时,考虑到给图像引入的冗余数据会降低运算速度,全零矩阵并不是越大越好。

图3 离轴全息的模拟再现Fig.3 Simulation reproduce of off-axis holography
4 实验验证
为了验证本文提出的方法,搭建了一套基于空间光调制器(spatial light modulator, SLM)的全息显示系统。系统装置图如图4所示,入射光波经过空间滤波,准直后照射到SLM上。选用的SLM(GCI-7701电寻址空降光调制器)为TFT-LCD透射式液晶屏,分辨率为1 024像素×768像素,像素间距为26 μm。SLM与CCD分别位于傅里叶透镜的前后焦平面上,用高通滤波器滤除零级光,然后由CCD接收最终图像。

图4 全息再现光路Fig.4 Holographic display system
实验中,将制作好的计算全息图通过计算机加载到SLM中,由CCD接收再现像,由于CCD视场有限,没有接收到由空间光调制器像素结构造成的其他衍射像。实验结果如图5(b)所示,可以看出,将原物抽样点写入600×600的全零矩阵中可以实现原始像与共轭像的分离,但再现像的散斑噪声很大,这是随机相位因子和实验硬件光路系统带来的随机噪声所造成的。可采用多幅图平均[11-12]的方法进行降噪处理,即将计算全息图在二维方向准确地周期平移,这样用准直激光照明再现像由多幅全息图合成的新的全息图时,根据傅里叶变换的平移不变性,便使单幅全息图的再现像能准确地叠加在一起,从而进行多幅图像的平均,达到降低散斑噪声的目的。但是经过周期延拓后的全息图尺寸会变得很大,而空间光调制器的尺寸有限,实验中SLM不能加载平移后的所有全息图,这里用Matlab来模拟实验中连续拍摄的100幅全息图的再现像叠加过程,来验证这种方法的可行性。仿真结果如图5(c)所示,再现像的散斑噪声在很大程度上得到了抑制。通过比较图5(c)与图3(d),可直观地看出,将原物抽样点镶嵌到600×600的全零矩阵中后再编码得到的计算全息图,以及通过实验光路系统得到的再现像中原始像和共轭像的分离程度,与模拟仿真结果相一致。

图5 实验结果Fig.5 Experimental results
5 结论
本文根据傅里叶计算全息图的原理和特点,研究了一种基于博奇型计算全息的编码方法,即将原物抽样点镶嵌到比原物大的全零矩阵中来达到离轴的效果。通过全息再现光学系统可得到准确的离轴再现像,并控制全零矩阵的大小来控制再现时原始像与共轭像的分离程度。借鉴数字图像降噪的方法,采用多幅图像平均的方法降低再现像的散斑噪声,提高了CGH的质量。实验结果表明,该编码方法再现图像效果良好。
[1] Susumu N,Ken M,Ichiro S,et al. Three-dimensional display system for medical imaging with computer-gengrated integral photography [J]. SPIE,2000,3957:60-67.
[2] Yang Guijuan,Mei Yan,Bai Yaxiang.Development and application of holography[J].Journal of Applied Optics, 2006,27(2):96-100.
杨桂娟,梅妍,白亚乡.全息术及其应用[J]. 应用光学,2006,27(2):96-100.
[3] Shen Xueju,Wang Yongzhong,Yao Guangtao.Design of matched filter based on analysis of background noise Fourier spectrum[J].Journal of Applied Optics, 2008,29(3):343-346.
沈学举,王永仲,姚广涛.基于背景噪声谱分析的匹配滤波器设计研究[J]. 应用光学,2008,29(3):343-346.
[4] Wang Yongzhong,Xue Rui,Zhang Yong,et al.Research and performance analysis of matching filters by computer generated hologram[J].Laser & Infrared, 2005,35(4):275-278.
王永仲,薛蕊,张勇,等.计算全息制匹配滤波器的研究及性能分析[J]. 激光与红外,2005,35(4):275-278.
[5] Pei Chuang,Jiang Xiaoyu,Ding Sheng,et al.Three-dimensional display of computer-gengrated hologram based on spatial light modulator[J]. Journal of Applied Optics,2013,34(5):772-777.
裴闯,蒋晓瑜,丁晟,等.利用空间光调制器实现计算全息三维显示[J].应用光学,2013,34(5):772-777.
[6] Chen Daqing,Gu Jihua,Zhou Hao,et al.An image digital watermarking with phase retrieval algorithm and Fourier transformation hologram[J].Acta Optica Sinica, 2009,29(12):1145-1149.
陈大庆,顾济华,周皓,等.基于相位恢复的傅里叶变换全息图像数字水印[J]. 光学学报,2009,29(12):1145-1149.
[7] Chen Jiazhen,Zheng Zihua,Lian Guiren,et al.Computer generated holographic watermark technology based on four detour phases encoding scheme[J].Laser & Opt. Electronics Progress, 2010,47(6):60901.
陈家祯,郑子华,连桂仁,等.基于四阶迂回相位编码的计算全息水印技术[J]. 激光与光电子学进展,2010,47(6):60901.
[8] Lohmann A W,Paris D P.Binary Fraunhofer holograms generated by computer[J]. Applied Optics,1967,6(10):1739-1749.
[9] Yu Zuliang,Jin Guofan.Computer generated holograph[M].Bejing:Tsinghua University Press,1984:48-58.
虞祖良,金国藩.计算机制全息图[M]. 北京:清华大学出版社,1984:48-58.
[10] Su Xianyu,Li Jitao.Information optics[M].Beijing:Science Press,2007:167-172.
苏显渝,李继陶.信息光学[M]. 北京:科学出版社,2007:167-172.
[11] Chen Zhenpei,Chen Huaixin,Dai Jianmin. A method based on average of multiple CGHs to eliminate the speckles of reconstruction[J].Optoelectronics Laser,1997,8(5):383-386.
陈祯培,陈怀新,戴建明. 减少计算全息再现散斑的多幅平均方法[J]. 光电子·激光,1997,8(5):383-386.
[12] Ma Jianshe, Ren Zhenbo, Su Ping,et al.Comparison and improvement of image quality evaluation of zero-order elimination methods in holographic reproduction[J]. Semiconductor Optoelectronics,2013,34(4):713-718.
马建设,任振波,苏萍,等.全息再现中几种消零级方法的像质评价及其改进[J]. 半导体光电,2013,34(4): 713-718.
