基于能量分布的红外像点定位分析方法
2014-03-27胡秋平
李 斌,刘 刚,胡秋平,刘 钊
(中国华阴兵器试验中心,陕西 华阴 714200)
引言
利用红外传感器对目标探测、定位,广泛应用于目标识别、预警和飞行状态分析。利用红外像点进行目标定位分析时,受成像器件分辨率及成像系统自身影响,实际应用中提出了多种方法,以获取定位结果,提高定位精度。通过插值细分获取高精度定位结果是常用方法,但文献[1-3]研究中重点关注了计算公式、噪声处理方法,对定位分析的理论依据研究较少;其他研究方法[4-5]如多帧叠加、微扫描处理等,主要是利用过采样获取冗余信息提高定位效果,或者采用相关软硬件提高系统分辨率,均以提高代价投入改进定位效果,使应用范围带有局限性。
针对红外像点定位分析问题,本文利用成像能量分布规律,通过对红外目标的成像进行分析研究,获取了红外像点定位分析模型及精度结果。理论分析及实例计算表明,该方法能有效分析红外像点定位特点及精度,在工程实际中有较高的应用价值。
1 红外目标成像特征
红外目标成像时,根据成像距离与目标尺寸的对比关系,可区分为点目标、面目标。用红外探测器探测远距离目标或近距离小目标时,即目标尺寸远小于探测距离,可将其视为点目标;当目标尺寸与探测距离相比不能忽略时,将其视为面目标。
1.1 红外成像扩散规律
对光学成像系统,用艾里斑衡量成像分辨率的极限,表示成像衍射扩散情况。根据光学衍射理论,艾里斑即红外成像一级衍射斑直径表示为
d=2.44λf/D
(1)
式中:λ为成像波段;f为焦距;D为通光口径。
若光学系统观测时垂直于衍射斑扩散方向,则艾里斑可直接用(1)式计算;若观测时与垂直方向存在一定角度,则根据几何投影关系,在(1)式基础上进行转换,获取成像衍射情况。
1.2 红外点目标能量分布模型
对点目标探测时,受光学系统点扩散函数的影响,目标的入射能量具有中心高、向外逐渐减弱的近似二维高斯分布的空间形态。红外点目标成像的艾里斑能量分布模型,可用高斯分布表示[6-7]如下:
(2)
式中:Emax为能量分布最大值;(x0,y0)为衍射斑能量中心;ax、ay分别为衍射斑能量分布长、短轴。
1.3 红外面目标能量分布模型
对红外面目标进行探测时,同样受点扩散函数的影响,与点目标区别的是:面目标相当于由若干点目标组成,其能量分布等效于多个点目标的合成。
在高斯能量分布模型下,对面目标位置(x,y)的能量,由其周围一定范围内的点斑能量分布合成获得,设该范围内任一衍射斑能量中心为(xi0,yi0),相应的能量分布最大值为Eimax,则在(2)式建立红外面目标的能量分布模型:
(3)
2 基于能量分布的定位分析方法
由红外成像的能量分布规律进行目标定位分析,首先将目标定位的基准位置确定为能量中心,如需实现目标上预定位置的定位,可以能量中心基准进行坐标变换;然后建立能量中心与能量分布、能量分布与成像灰度之间的对应关系,将目标定位转化为图像分析过程。
2.1 能量中心计算
能量中心是对目标能量值的加权运算,权值大小与距离能量中心的距离成正比。结合目标能量分布模型,则能量中心计算式如下:
(4)
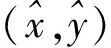
2.2 数字图像灰度分析
利用红外焦平面探测器获取目标图像时,主要获取入射能量大小与图像灰度数值的关系。此时照射在焦平面上某一个探测像元的能量大小Eij,相当于该像元所在i、j区域能量,则Eij与能量分布E(x,y)有下式关系:
(5)
目标能量分布通过非均匀性校正,使各探测元参数具有相同的响应特性,则在红外探测器线性响应模型如下,像元的响应灰度数值Hij为
Hij=Eijk+b
(6)
式中:k和b分别为该探测元的增益系统和偏移量。
由图像灰度进行能量中心计算时,根据(4)式及(6)式得:
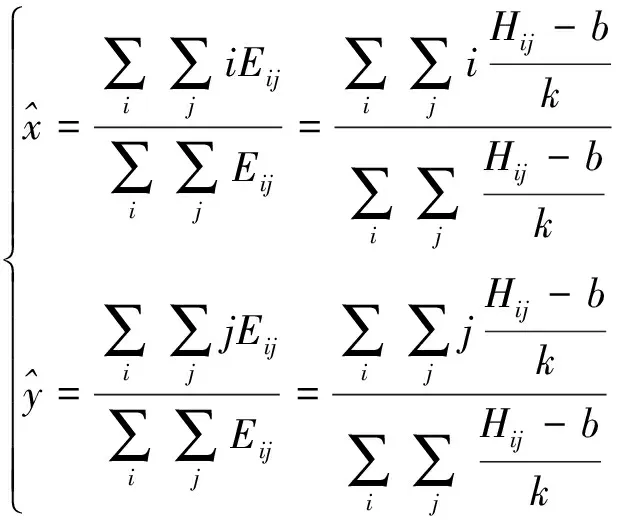
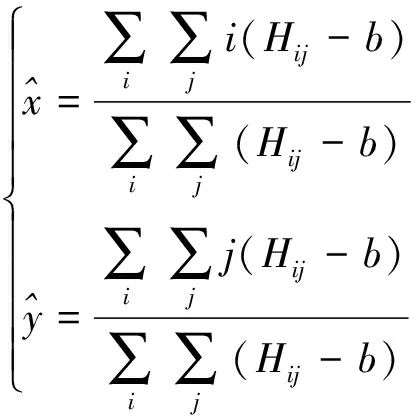
(7)
式中:b为Eij为0时的数值,可作为目标、背景的分割阈值,通过灰度均值运算、背景灰度统计等方法获取。
(7)式建立了目标能量中心与图像灰度的关系,在获取图像信息的基础上,可实现目标定位。
2.3 定位方法实现流程
根据能量分布实现定位的分析,结合精度分析一般过程,建立如下方法流程:
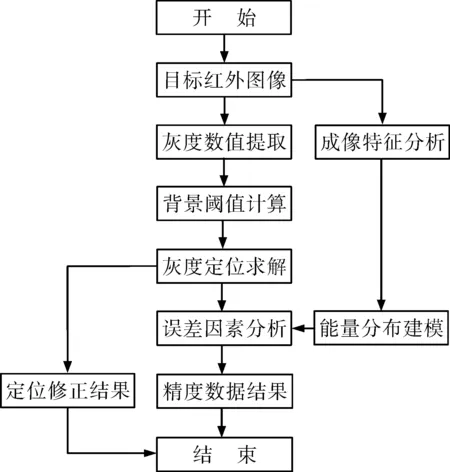
图1 方法流程图Fig.1 Flow chart of method
3 定位精度分析
在红外像点定位分析中,能量中心的求解运用了大量简化、近似的方法,下面进行具体分析,以确定定位结果精度。
3.1 误差影响因素分析
红外像点定位过程,主要包括[7-9]能量扩散、能量分布、成像数字化、探测相应、灰度运算等环节,定位误差主要涉及各环节采用的模型或分析方法。
1) 能量衍射级数
在能量分布只考虑一级衍射的情况下,约有84%的光能量集中在该一级衍射斑,对于艾里斑的定位分析具有主要作用,其余16%的光能量分布在各级明环上。由于多级衍射能量中心与一级衍射能量中心是一致的,且有序分布于能量中心周围区域,理论分析及实验测试表明,多级衍射不降低能量中心计算精度。在准确分析成像模型的情况下,多级衍射甚至能提高定位精度,光学工程常采用离焦的方法,人为改变多级衍射能量分布,以提高定位精度或获取特定使用效果。
2) 能量分布形态
目标能量分布的大小、形状,与入射光的分布特点、观测角度等因素相关,在面目标成像、非垂直于衍射斑扩散方向观测时,将影响能量分布的对称性和衍射形状,具体情况是:
在目标为点目标且垂直观测时,能量分布具有对称性、圆形等特点,可在此基础上分析其他能量分布情况;
在目标为点目标非垂直观测时,能量分布呈现对称性、非圆形,该分布形态不降低能量中心计算;
在目标为面目标非垂直观测时,能量分布合成情况为每一点目标能量叠加,该分布形态不降低能量中心计算;
在与垂直观测方向角度较大时,能量将分布于较大的成像区域,这相当于通过成像细分进一步提高了定位精度。
3) 数字化采样
红外探测数字化采样过程,是探测器像元对能量分布的空间采样,空间采样率对定位分析有直接影响:点目标成像时,可能存在采样率低影响精确定位的问题;面目标成像时,由于自身尺寸远大于像元尺寸,可视作对点目标更精细的空间采样,采样率影响作用远小于点目标。
4) 探测响应模型
红外探测器的线性响应模型,是在光电转换基础上建立的,存在标定范围对测量的适应性、探测器自身噪声等因素,另外由于制造工艺的限制,焦平面探测器的填充率小于100%,处于像元之间的目标能量无法响应。这些因素对目标灰度、背景灰度将产生影响。在制冷型红外焦平面器件实际统计中,探测模型引起的误差可控制在10%以内,文献[10]描述了一组使用中获取的探测响应情况,精度达到了6.65%。采用精确的探测响应模型,可有效控制探测响应误差。
5) 背景噪声
利用阈值对目标、背景进行图像分割,理想的阈值数值能恰好去除背景,完全保留目标信息,而实际情况中往往难以做到:或者阈值略小,存在部分背景噪声;或者阈值略大,去除了部分目标信息。典型使用环境下,噪声灰度可控制在5%以内,文献[10]给出了2.11%的实际统计值。
6) 探测器疵点
红外探测器的疵点会严重影响探测器响应误差,甚至出现坏点,由于这些像元数量很少且极少连续出现,可以考虑规避该类像元、灰度插值重构、多次冗余测量等方法进行解决。
综合上述定位误差影响的因素,除数字化采样这一因素,其他均得到了定性或定量结果。下面结合点目标、面目标成像,进一步分析数字化采样与定位精度的关系。
3.2 数字化采样对点目标定位影响
典型点目标成像如图2,根据探测成像数字化采样情况,艾里斑直径与像元尺寸在同一量级,能量分布于一个或相邻的多个像元。探测器靶面像元对艾里斑采样时,以每一像元的几何中心表示该像元位置,而相应成像能量中心的真值并不一定在几何中心,例如图中像元Ⅱ所示,可直观判定能量中心并非在像元几何中心。每一像元几何中心与成像能量中心的不一致性,造成了数字采样对目标定位的误差。
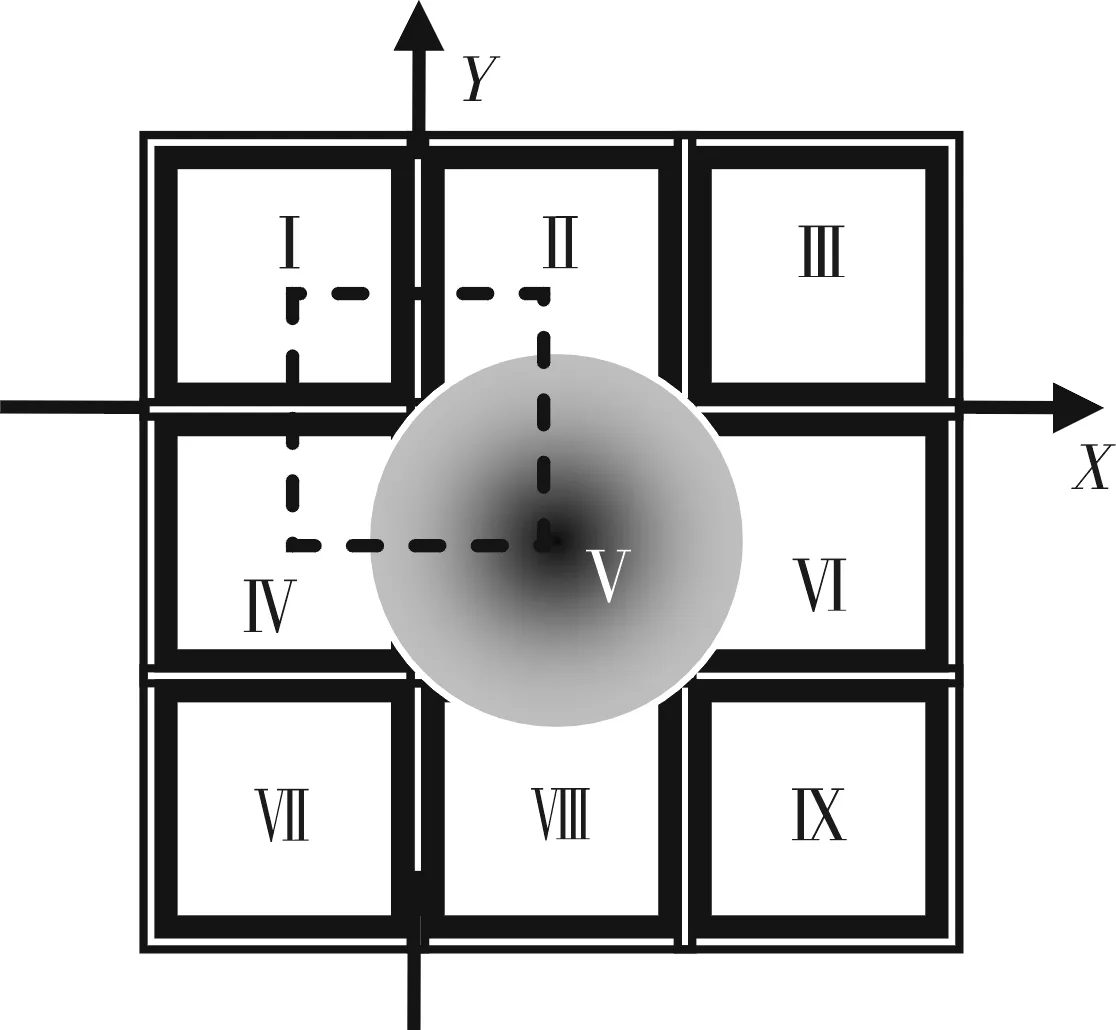
图2 艾里斑成像位置变化图Fig.2 Variations of Airy disk position
对图2中艾里斑进行定位,在不影响误差分析结论的普遍意义前提下,作如下简化分析,按垂直入射于探测器靶面进行成像分析,简化分析过程:
1) 建立坐标系如图,由于定位误差规律在X、Y两方向相同,可任取一方向分析,下文取Y方向;
2) 艾里斑能量中心沿图中虚线框表示的正方形区域变化,正方形任一边为相邻像元几何中心的连线;
3) 由于艾里斑能量中心处于一像元的几何中心或两像元边界时,定位误差为0,因此对艾里斑能量中心由像元Ⅴ的几何中心向上变化至边界的过程予以重点分析。
在上述简化后,设像元大小为a,艾里斑直径为d,衍射斑能量中心实际位置x=a/2,对任一y∈[-a/2,0],像点分布于图2中区域,据(7)式可得位置 :
(8)
对于特定光学系统及焦平面成像进行定位分析,由于涉及的光学系统参数、焦平面器件像元尺寸是确定的,对定位分析产生影响作用的特征波长,主要是如图3中所示2种特征情况:一是艾里斑直径与像元尺寸相当,像元恰好能容纳1个艾里斑;另一种情况是,艾里斑直径与像元对角线尺寸相当,艾里斑恰好能充满1个像元。
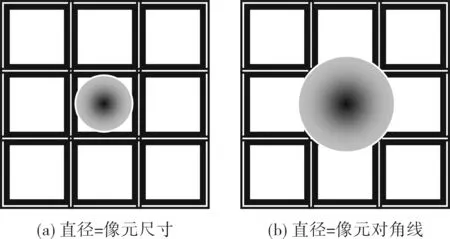
图3 艾里斑与像元尺寸比较图Fig.3 Airy disk and pixel size
这里取图3(b)特征情况进行分析:定位误差开始为0,艾里斑向上移动,所得位置变化率小于能量中心变化率,产生误差为负值并逐渐累加,继续向上移动,则存在一个位置,定位误差绝对值最大,此时所得位置变化率等于能量中心变化率,如图4所示。当艾里斑上半部分能量被像元分界点平分时,满足位置变化率等于能量中心变化率。此时,对能量进行合成运算,可知能量中心真值为-0.101d,数字化采样后获取的位置为-0.25a,即:
δmax=|-0.25a+0.101d|=0.25a-0.101d
(9)
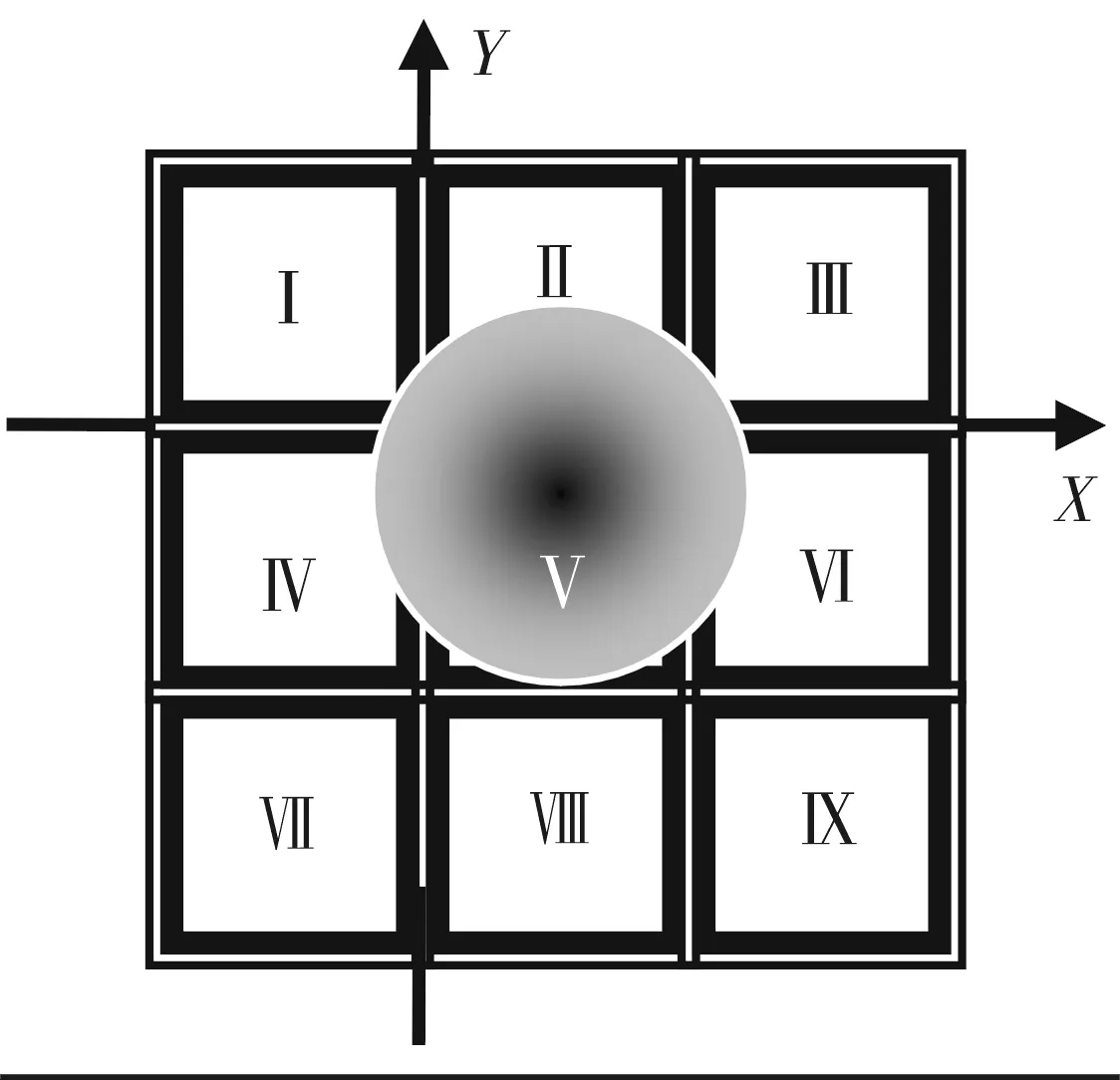
图4 最大定位误差分析图Fig.4 Maximum error of position analysis
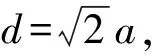
δmax=0.107a
(10)
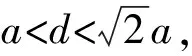
0.149a<δmax<0.107a
(11)
d=a,即艾里斑与像元尺寸相当:
δmax=0.149a
(12)
当d d δmax=0.75a-0.601d (13) 当d=2.475a时,δmax=0,此时艾里斑尺寸较大,能量中心变化构成已经历了误差由0变大再到0的过程,则 δmax<0.107a (14) d>2.475a,即艾里斑远大于像元对角线尺寸: δmax≪0.107a (15) 由数字化采样对点目标定位影响分析过程,根据(9)式及(15)式可知:面目标定位过程相当于艾里斑远大于像元尺寸的情形,此时,数字化采样对面目标定位影响较小,可以参考两式进行分析。 在误差影响因素以及数字化采样重点分析基础上,利用误差传播定律对(7)式进行误差分析。 按探测模型引起的误差10%,噪声灰度误差5%,数字化采样误差δ,略去高阶误差小项,则总误差为 (16) 在工程应用中,可按δmax由(9)式~(15)式给出精度结果。在常用的红外系统中,艾里斑直径一般不小于像元尺寸,据(12)式其定位误差优于1/6像元,在像点较大时,定位误差可达1/10像元甚至更高精度。 对于某典型的中波红外探测成像系统,焦距f=700 mm,通光口径D=200 mm,焦平面器件像元尺寸为30 μm×30 μm,则有: 1) 当λ=5 μm时,艾里斑直径为 d=2.44λf/D=42.7 μm 2) 当λ=3 μm时,艾里斑直径为 d=2.44λf/D=25.6 μm 在近似为均匀能量分布下,定位按3 μm~5 μm波段艾里斑均值进行分析: 0.149a<δmax<0.107a δmax=0.135a 即定位精度优于1/7像元。 本文针对红外像点定位问题,对像面能量分布规律与目标成像特点进行了综合研究,提出基于像面能量分布的定位及精度分析方法,理论分析和实例计算表明,该方法实现了红外探测系统定位的精确分析,在常用红外系统应用的定位精度可达到1/6像元以上,在成像较大时定位精度可提高到1/10像元以上,对于红外测量数据应用具有重要意义,为空间定位、飞行体测量精度分析奠定了技术基础。在后续研究中,可深入研究对定位精度具有影响的各技术环节,进一步提高具体工程应用效果。 [1] Wei Wei,Liu Enhai.Preprocessing of infrared star map and position accuracy analysis of star point[J].Infrared and Laser Engineering,2014,43(3):991-996. 魏伟,刘恩海.红外星图预处理及星点定位精度分析[J].红外与激光工程,2014,43(3):991-996. [2] Xie Lunzhi,Bian Honglin,Wang Zhenhua.Study of the subpixel interpolation of image spots with matrix detectors[J].Optics and Optoelectronic Technology,2003,1(2):51-56. 谢伦治,卞洪林,王振华.面阵探测器的像点亚像素定位研究[J].光学与光电技术,2003,1(2):51-56. [3] Tang Shengjin,Guo Xiaosong,Zhou Zhaofa,et al.Modified systematic error compensation algorithm for star centroid sub-pixel detection[J].Infrared and Laser Engineering,2013,42(6):1502-1507. 唐圣金,郭晓松,周召发,等.星点亚像素定位中系统误差的改进补偿方法[J].红外与激光工程,2013,42(6):1502-1507. [4] Li Qinghui.Study of spatial resolution improving of infrared imaging system[J].Spacecraft Recovery and Remote Sensing,2003,24(2):25-28. 李庆辉.提高红外成像空间分辨率的方法探讨[J].航天返回与遥感,2003,24(2):25-28. [5] Shi Xun,Hou Liwei,Pan Ming,et al.Accurate localization of moving point target[J].Chinese Journal of Radio Science,2009,24(4):766-769. 石勋,侯丽伟,潘鸣,等.运动点目标精确定位方法研究[J].电波科学学报.2009,24(4):766-769. [6] Wei Zhenzhong,Gao Ming,Zhang Guangjun,et al.Sub-pixel extraction method for the center of light-spot image [J].Opto-Electronic Engineering,2009,36(4):7-12. 魏振忠,高明,张广军,等.一种光斑图像中心的亚像素提取方法[J].光电工程,2009,36(4):7-12. [7] Xu Nanrong,Bian Nanhua.Infrared radiation and guidance [M].Beijin:National Defence Industry Press,1997:96-101. 徐南荣,卞南华.红外辐射与制导[M].北京:国防工业出版社.1997:96-101. [8] Yi Yaxing,Yao Mei,Wu Junhui,et al.Factors of the detected luminance of an infrared target[J].Infrared and Laser Engineering,2014,43(1):13-18. 易亚星,姚梅,吴军辉,等.影响红外目标探测亮度的因素[J].红外与激光工程,2014,43(1):13-18. [9] Wang Hantao,Zhao Baojun,Tang Linbo. Trajectory extraction algorithm of moving point targets star background [J].Optical Technique,2009,35(6):810-814. 王寒涛,赵保军,唐林波.星空背景下的运动点目标轨迹提取[J].光学技术,2009,35(6):810-814. [10] Li Bin,Wu Haiying,Wang Wentao, et al. Design of a simple infrared calibration system[J].Infrared and Laser Engineering,2014,43(2):458-463. 李斌,吴海英,王文涛,等. 一种简易红外标定系统的设计[J]. 红外与激光工程,2014,43(2):458-463.
3.2 数字化采样对面目标定位影响
3.3 综合定位精度分析
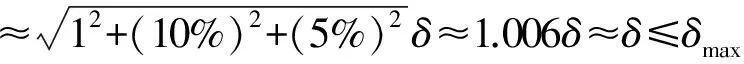
4 实例计算
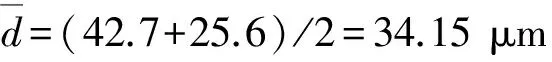
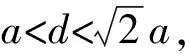
5 结论
