特定边界跟踪中角点检测研究

田军委，王 沁，赵 鹏,王岗罡

(1.西安工业大学 机电工程学院，陕西 西安 710032；2.中国人民解放军驻211厂军事代表室，北京100076)

引言

在特定边界检测中，边界跟踪是常用的一种方法，而边界跟踪中较多采用“爬虫”跟踪算法[1-3]。由于这类算法要跟踪完所有的轮廓边界点，而且，边界跟踪仅利用图像局部信息，没有利用全局信息作为先验知识，造成信息浪费和跟踪效率较低。目前又出现了一种抽取边界点的边界跟踪算法，这种算法从反映边界信息的角度出发，检测部分边界点，实现特定轮廓跟踪。这种方法检测效率高、稳定性好，但由于采用等步长采样，往往检测不到角点，并且在角点附近存在大量信息丢失现象，因此必须采用角点检测算法检测出角点，保证边界跟踪的正确性和准确性。

角点是图像轮廓发生突变的点，反映了物体轮廓特征，有时又称为特征点，是模式识别和图像处理中要处理的最小化数据。由于角点在数字图像处理中的重要作用，研究人员提出了各种角点检测算法，如Cooper等人利用链码处像素坐标估计最大曲率值来寻找角点[4]。Ponce和Brady利用图像I(x,y)对x、y的偏导数来寻找角点[5]。Hsin-Teng和Hu则使用多边形近似边界链，然后把两边的交点作为角点[6]。Kitchen和Rosenfeld[7]采用目标边缘梯度方向的曲率变化率来检测角点。Zuniga和Haralick[8]采用最小二乘法用三次多项式曲面拟合数字图像，先检测出边界点，然后计算该点的梯度方向角在梯度方向的变化率，大于某阀值时，则认为该边界点是角点。Wang和Brady[9]先利用高斯滤波器卷积原始图像，然后计算图像的表面曲率，最后通过阈值技术来检测角点。Medioni和Yasumoto[10]利用B-样条拟合边界的方法来检测角点，把计算得到的曲率最大值的点检测为角点。Beaudet[11]通过对图像函数二阶导数的泰勒展开，得到Hessian矩阵H(x,y)，该矩阵具有旋转不变性，可以直接对灰度图像进行操作提取角点。Smith等人[12]提出了一种低层次图像处理小核值相似区的方法(简称SUSAN算法)。Trajkovic等人[13]在角点响应函数(CRF)的基础上提出一种新的角点检测算法。Noble[14]提出了一种数学形态学的角点检测方法，利用形态运算A-AoB来检测凸型角点，利用AgB-A来检测凹型角点。Robert[15]提出了使用非对称闭运算来检测角点。

这些算法都能够成功检测到角点，但是，对于固定步长边界跟踪算法，这些角点检测算法或者不适定，或者计算效率低。为了在固定步长边界跟踪中快速、正确地检测到角点，本文提出了寻区间角点检测算法。

1 特定边界跟踪

特定边界跟踪[16]思想是：根据待检测边界的连续性和对该边界的先验知识，以欧氏距离为度量，搜索过程分为边界点预估计和边界点搜索两步。

1.1 边界点预估计

Δki-2=ki-1-ki-2∈[Δkmin,Δkmax]

(1)

Δki-1=ki-ki-1∈[Δkmin,Δkmax]

(2)

式中：ki为vi和vi+1连线的斜率。

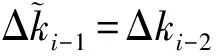
(3)

(4)

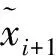
边界点预估计原理如图1所示。

图1 边界点预估计原理Fig.1 Principle of boundary points estimation

1.2 边界点搜索

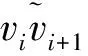
(5)

2个搜索方向为

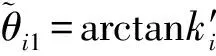
(6)

图2 边界点双向搜索原理Fig.2 Principle of boundary points bidirectional searching

双向邻域扩展中，其中一个搜索方向是冗余的，为了进一步提高搜索效率，可采用准双向邻域扩展搜索算法，优先搜索方向可以利用边界在该范围的凹凸性来判别。

(7)

根据函数凹凸性判别准则，如果

yi>K(yi-1+yi)

(8)

成立，则该区间内待检测边界是上凸的，如果

yi

(9)

成立，则边界在该区间是上凹的，定义vi+1可能存在的方向为边界在该处凹陷的一侧。

2 角点存在判别

由于待检测边界上往往存在角点，要完成跟踪并得到正确的检测结果，必须正确检测出角点并给出合理的种子点以完成后续边界跟踪。

设vi是边界y=C(x)上的一个角点，则在vi处y=C(x)的左右导数不相等。

(10)

在实际边界跟踪中一般无法确知y=C(x)的解析式，需要用判别算法识别轮廓角点。

(11)

当vi和vi+1之间存在角点时，角点两侧的一阶导数出现跳变。实际搜索情况如图3所示。对两种人工图像进行实验，结果如图4所示。

图3 角点附近边界跟踪情况Fig.3 Boundary tracking near corner point

图变化情况实验Fig.4 Examination for trends

(12)

如果角点存在，角点va所处的区间为va∈[vi,vi+1]。

3 角点检测

设vi为角点，边界y=C(x)在y处左右导数为

(13)

(14)

式中，δ>0。设vi-1和vi+1分别为角点vi两侧的边界点，用直线vi-1vi和vivi+1的斜率近似y=C(x)在vi处的左右一阶导数，则有：

(15)

(16)

如果vi不是角点，根据(1)式和(2)式的结论，有Δki-1=ki-ki-1∈[Δkmin,Δkmax]；如果vi是角点，由于y=C(x)的一阶导数在vi处发生跳变，有如下关系：

Δki-1<Δkmin或Δki-1>Δkmax

(17)

对Δkmin和Δkmax进行归一化处理，(17)式就可以写成：

|Δki-1|>ΔkthΔkth=max{|Δkmin|,|Δkmax|}

(18)

这样，利用三点之间连线斜率关系可以检测出角点。这种方法称为寻点法，但在搜索过程中，如果采用逐点搜索，Δk是一个渐变量(由边界的连续性可知)，满足(18)式的点往往有许多，其中|Δk|最大者才是真正的角点，用这种方法搜索角点时，必须进行二次判断。为了快速准确地找到角点，我们提出了一种寻区间法。

设vi-2、vi-1、vi、vi+1和vi+2均为待检测边界上的点，且角点两侧至少有2个边界点，定义：

Δkp=|Δki+1-Δki-2|

(19)

容易证明，如果Δkp>Δkth，那么角点必在vi的某一邻域内，当区间vi足够小，且搜索步长选择合理(大于像素本身产生的微观角点)，第一次满足(18)式的点vi就是角点。这种方法用寻找区间来代替寻找某个点，从而易于判别，且效率大大提高。

4 实验及分析

对本文所提出的角点检测方法，用不同的图像进行检测，图5是对测试图像1进行跟踪的结果，图6是对人脸侧面图像嘴巴附近图像进行处理的结果。

由实验结果可以看出，当没有对所检测轮廓角点进行判断和检测时，边界跟踪所得到的边界点就会在角点附近出现大段缺失，因而丢失了许多有用的边界信息。由图5(a)和图6(a)的跟踪结果还可以看出，边界跟踪丢失的信息和角点附近轮廓边界变化情况有关，当角点附近轮廓边界变化剧烈，两边边界夹角小，边界点缺失距离就大，丢失的边界信息也多，图6(a)所丢失的边界信息就明显地多于图5(a)。当在边界跟踪过程中加入边界点判别和检测处理，边界跟踪中就能够越过边界点，正确进行后续边界跟踪，不丢失后续轮廓的信息。图5(b)和图6(b)的结果表明，两种方法得到边界点数量分别为19、37和13、21，在边界跟踪过程中本文所提出的算法均能够正确判断出角点位置检测到该角点，然后植入有效的种子边界点，使后续跟踪能够完整跟踪完后续边界。由于所检测的边界点反映了待检测轮廓的所有信息，因此在后续建模中才有可能建立正确的轮廓模型。

图5 测试图像1实验结果比较Fig.5 Experiment comparison of test image 1

图6 人脸嘴巴附近图像实验结果比较Fig.6 Experiment comparison of side face image

5 结论

实验结果表明：

1) 本文所提出的特定轮廓边界角点判别准则在不增加计算量的情况下能够准确判断出角点所在的区间；

2) 在判断出的角点所在的区间内，采用寻区间检测算法能够快速准确检测出角点，并从角点开始给出正确的种子，为后续边界跟踪提供正确的初始条件；

3) 采用角点判别和检测方法的边界跟踪算法能够检测到正确的轮廓边界，且不丢失轮廓变化的重要信息；

4) 由实验结果可以看出，角点附近所检测到的边界点比较密集，和边界的变化情况关系不密切，存在冗余边界点，有待提出有效的约束，去除冗余边界点。

[1] Sobel L. Neighborhood coding of binary images for fast contour following and general binary array processing[J]. Computer Graphics Image Process, 1978, 8(1):127-135.

[2] Liow Y T. A contour tracking algorithm that preserves common boundaries between regions[J]. CVGIP-Image Understanding, 1991,53(3): 313-321.

[3] Wang Yu, Lu Yanpin, Zhang Zehong, et al. A reptile method with memory and alterable window for image boundary tracing[J]. Chinese Journal of Scientific Instrument, 2004, 25(4):383-491.

王珏, 卢艳平, 张泽宏,等. 一种有记忆的变窗“爬虫”图像边界跟踪方法[J]. 仪器仪表学报,2004 ,25(4):483-491.

[4] Cooper J, Sveth A, Kitechen L. Early jump-out corner detectors[J]. IEEE Transactions on PAMI, 1993(15):823-828.

[5] Ponce J, Brady M. Towards a surface primal sketch[C]. St.Louis, MOUSA： In: IEEE International Conference on Robotics and Automation, 1985:420-425.

[6] Hsin Teng, Hu W C. A rotationally invariant two-phase scheme for corner detection[J]. Pattern Recognition, 1996,28(5):819-829.

[7] Kitchen L, Rosenfeld A K. Gray-level corner detection[J]. Pattern Recognition Letters, 1982,3(1):95-102.

[8] Zuniga O A, Haralick R. Corner detection using the facet model[C]. Washington D.C.： IEEE VCPR, 1983:30-37.

[9] Wang H, Brady M. Real-time corner detection algorithm for motion estimation[J]. Image and Vision Computing,1995,13(9):695-703.

[10] Medioni G, Yasumoto Y. Corner detection and curve representation using cubic B-spline[J]. Compute Vision, Graphics, Image Process, 1987,39(3):267-278.

[11] Beaudet P R. Ratationally invariant image operators [C]. Kyoto, Japan：Internat. Joint Conf. on Pattern Recognition, 1978:579-583.

[12] Smith S M, Brady J M. SUSAN-a new approach to low level image processing[J]. Journal of Computer Vision, 1997,23(1):45-78.

[13] Trajkovic M, Hedley M. Fast corner detection[J]. Image and Vision Computing, 1998,16(1):75-87.

[14] Noble J A. Image as functions and sets[J]. Image and Vision Computing, 1992,10(1):19-29.

[15] Robert L. A morphological operator for corner detection[J]. Pattern Recognition, 1998,31(11):1643-1652.

[16] Tian Junwei, Huang Yongxuan, Pan Wanying. Adaptive step-size fast interested boundary tracking[J]. IEEE, 2007(5-8):2395-2398.

[17] Yoon J S, Park J C, Jang S W, et al. A shakable snake for estimation for image contours[J]. ICCSA, LNCS,2004, 3043: 9-16.