捷联惯性导航系统误差工程化分析方法

郭栓运，马忠孝，许开銮，康 臻，贺峻峰

(西安应用光学研究所，陕西 西安 710065)

引言

陀螺和加速度计是捷联惯性导航(SINS)的核心器件，其性能直接影响SINS的性能，如何根据总体系统对SINS的指标需求合理选择陀螺和加速度计是设计SINS所必需解决的首要问题，这需要系统设计人员对SINS精度指标与陀螺和加速度计性能之间的关系有一个清楚的理解。SINS的主要性能指标包括：定位精度、速度精度、姿态及航向精度，这些指标都直接受惯性传感器指标的影响。国内外在设计SINS时，传统做法是：根据SINS的误差传递模型进行复杂的误差模型确定、误差参数设定和仿真分析[1]，既费时又费力，且分析结果往往与实际相差较大，因为理论上的误差模型不便于在实际工作中对SINS各指标的关系及与惯性传感器性能之间的关系进行直观的分析，实际的仿真模型需要根据丰富的工程经验进行模型的工程化。本文结合设计SINS的工程经验，在分析SINS各项指标间的关系及它们与惯性传感器性能之间关系的基础上，从SINS的2个工作阶段，即对准阶段和导航阶段进行分析，根据不同SINS的工作需求提出了SINS主要误差源与导航指标间的简化换算关系，给出了设计SINS及分析其性能更简洁而实用的工程方法,与传统方法相比，可提高工作效率50%以上。

1 SINS对准精度与陀螺、加速度计的指标分析

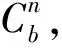
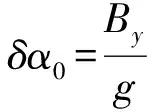
(1)

式中：By为东向加速度计零偏；Bx为北向加速度计零偏；Dy为东向陀螺零偏；Ω为地球自转角速率；L为当地地理纬度；δα0、δβ0、δγ0分别为初始俯仰角误差、横滚角误差和航向角误差。

通常，当系统未与地理坐标系对准时，上述方程中的敏感器零偏将由3个陀螺零偏或3个加速度计零偏的线性组合构成，但在系统设计时完全可以按照(1)式来考虑。

在航向角误差δγ0，第一项是剩余陀螺零偏作用于东向的结果；第二项是北向轴的调平或倾斜误差，它使得地球速率的垂直分量(δαΩsinL)等效成为关于东向轴的另外零偏。根据(1)式，当选用的加速度计零偏优于0.1 mg时，将引起0.1 mrad的水平对准误差和0.1 mrad方位对准误差(45°纬度上)，而0.01°/h的陀螺漂移在45°纬度上将导致 1 mrad的方位对准误差，另外，目前国内加速度计，一般在设计高精度捷联SINS时，选择零偏优于0.1 mg的加速度计。

上述表述的是用一组测量数据进行对准的情况，这种方法只能进行粗对准。为了得到方向余弦阵更精确的估值，需要进行后继连续测量方向实现一段时间内的自对准。在这种情况下，通常对测量数据进行卡尔曼滤波或采用最小二乘法进行滤波，可在一定程度上提高系统对准精度，根据经验可以将系统精对准误差工程化成(2)式：

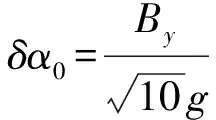
(2)

2 SINS导航阶段误差分析

2.1 SINS中时间导航误差分析

SINS的主要性能指标包括：定位精度、速度精度、姿态及航向精度，这些指标都直接受惯性传感器指标的影响，且各指标之间又有相应的转换关系，表1第2列给出了对于中时间导航的SINS的位置误差与各主要误差源的误差传递方程[2]。一般，这一模型对于中高精度的SINS要求中时间惯性导航才有实际意义。

表1 SINS中短时间的位置误差Table 1 Position error during short time of SINS

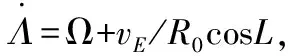
通常，可按照载体在良好工作情况下，根据表1中时间导航误差方程，估算SINS位置误差随时间因相应误差源引起的增长情况。图1为几种误差传播曲线，描述了SINS位置误差在3 h内随时间的增长情况。这里，为了便于说明，假定载体在匀速运动，同时水平对准精度设定为0.003°(1 σ)，方位对准精度设定为0.057(1 σ)，初始速度误差为0.5 m/s，陀螺零偏与加速度计零偏分别设为0.01°/h和10-5g(1 σ)，初始速度设为20 m/s。

图1中，最上面的曲线代表几种单一误差的综合结果。该曲线是通过计算这几种单一误差的平方和得到的总导航误差传播曲线。从图中可以清楚地看到，陀螺零偏与方位失准角的影响随时间的增加而快速增加，而其他误差项由于休拉调谐而受到限制。这一情况明确说明了陀螺的性能及初始对准对SINS导航性能的重要性。

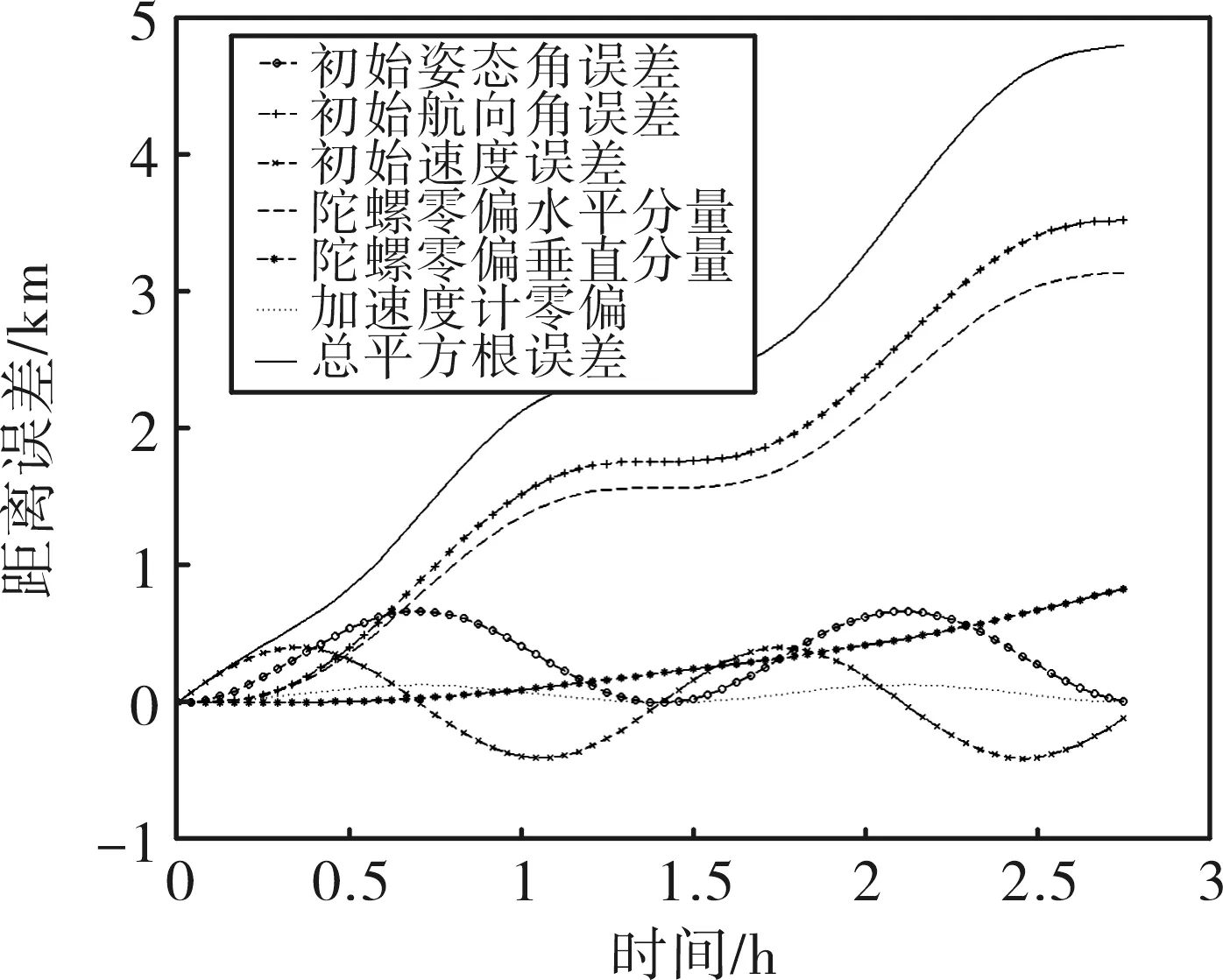
图1 惯性导航系统误差传播Fig.1 Error propagation of SINS

2.2 短时间SINS误差分析方法

以上对SINS在惯性导航模式下，中时间的导航误差分析。但在多数情况下，由于有其它导航方式(如卫星导航、天文导航、里程计、多普勒等)与SINS进行组合实现组合导航，或在某些领域(如制导弹药，空投空降等)SINS独立惯性导航的时间只需几分钟或更短，短时间的导航误差分析可进一步简化。

在短时间的SINS误差分析中，由于纯惯性导航时间一般不超过5 min[3]，所以在分析各种误差源对惯SINS的影响时，可以不考虑休拉调谐的影响，则各主要误差源与SINS误差之间的误差方程为表1第2列右列所示[3]，它是根据SINS的工作特点对简化后的误差模型进行分析，并根据工程经验对部分误差源给出更实用、简洁的误差分析模型。

2.2.1 初始姿态，航向误差与速度、定位误差的关系

为了分析方便，假设SINS航向角为0，则在载体平稳运动时(若无特殊说明，后文分析假设条件同上)，设系统初始横滚角、俯仰角、航向角误差分别是δα0、δβ0、δγ0，因为都是小角度，按照惯性导航原理，系统在开始导航到时间t时，因以上误差引起的速度和位置误差的公式推导如下：

(3)

(4)

对于初始航向误差，如果载体短时间运动，运动范围有限，可将载体运动简化成在一个平面上运动，则估算时航向误差造成的定位误差δP可忽略地球自转造成的影响，δP可简化为只与航向误差δγ0、载体的平均地速vg及时间t有关的模型：

(5)

式中:δvet、δvnt、δvgt分别为东向速度、北向速度和地速误差，单位为m/s；t为导航时间，单位为s；g为重力加速度，单位为m/s2；δλ、δL、δP分别为地理纬度误差、经度误差、地理位置误差，单位为m。

2.2.2 加速度计零偏与速度、定位误差的关系

若只考虑加速度计零偏误差时，则单通道系统速度位置误差公式为

(6)

(7)

式中：δv为速度误差；δBaN为一个水平方向的加速度计零偏；δP为位置误差；t为导航时间。

在设计SINS时，通过系统误差补偿可以补偿很大一部分加速度计零偏，所以选择加速度计时，其零偏指标可根据补偿后的指标选择确定。

2.2.3 陀螺主要性能对系统性能的影响分析

根据SINS工作原理，系统对准结束(建立初始姿态阵)进入导航后，姿态阵的更新就靠正交安装在载体坐标系上的3个陀螺实时测量的载体坐标系相对惯性坐标系的角速率，通过导航计算机将其转换为载体坐标系相对导航坐标系的角速率并积分成角增量后完成。所以，陀螺的测量精度是影响姿态阵精度最主要的因素。

2.2.3.1 陀螺零偏对系统精度的影响分析

根据工程经验，在短时间内，航向、姿态角的误差在考虑陀螺零位残余及零偏稳定性的影响时，各误差如下：

(8)

一般，根据工程实际，在SINS导航过程中，短时间内陀螺的零偏稳定性对系统姿态影响相对零偏残余量是一个小量，上式可简化为

δφ=ω0zt

δθ=ω0xt

δγ=ω0zt

(9)

综合(3)～(5)式及(8)～(9)式得出陀螺零偏对系统速度及定位精度的影响模型如下：

(10)

(11)

2.2.3.2 陀螺其他性能对系统的影响分析

以上分析都是假设系统在相对平稳或静止情况下的结果，如果系统在动态导航时，陀螺刻度系数的稳定性将是影响系统姿态精度很重要的因素，例如，如果陀螺刻度系数稳定性为1×10-3，则惯导系统航向在瞬间单方向转动360°时航向的误差将达到0.36°，姿态单方向转动90°时，姿态角误差将达到0.1°，这样再结合上文的分析，就可直观得出其对系统定位指标有很大的影响，另外陀螺与g有关零偏、陀螺非等弹性零偏等对系统的影响都可参照陀螺固定零偏对系统影响分析的方法进行。

3 设计举例

3.1 需求背景及情况介绍

要求在3个月内为某系统研制SINS，该SINS依赖卫星导航系统提供的位置、速度信息实现空中动基座对准，载体动态情况：水平加速度为1 m/s2，水平方向速度约为15 m/s，要求纯惯性导航120 s的情况下，导航精度为1 σ，航向精度为1.5°，姿态精度为0.8°、位置精度优于100 m。

3.2 误差预估及分配

根据系统要求及工作特点，本系统属于短时间导航(导航时间只是休拉周期很小的一部分)，可按照上文短时导航工程分析方法并基于最小风险策略的敏感器误差预估 1 σ和平方根位置误差，对系统技术指标进行分析。

系统的误差源主要包括：初始对准误差、加速度计误差和陀螺误差。SINS定位误差主要由这些误差引起。根据前期的仿真分析，为了完成动基座对准功能，系统必须配备磁航向传感器来提供初始航向信息，并依靠卫星导航系统提供的位置及速度作为量测量基准，通过卡尔曼滤波方法完成动基座初始对准。项目中配置动态精度优于1°的磁航向传感器，系统配置光纤陀螺零偏稳定性优于2°/h，石英振梁加速度计零偏优于0.1 mg，系统动基座初始对准，航向主要靠磁航向传感器性能保障，初始对准指标：航向误差≤1°、姿态误差≤0.03°、位置误差≤15 m、速度误差≤0.2 m/s(注：初始速度和位置误差主要由卫星导航系统决定)。则按照工程分析方法120 s内的惯导位置定位误差估算如表2所示。

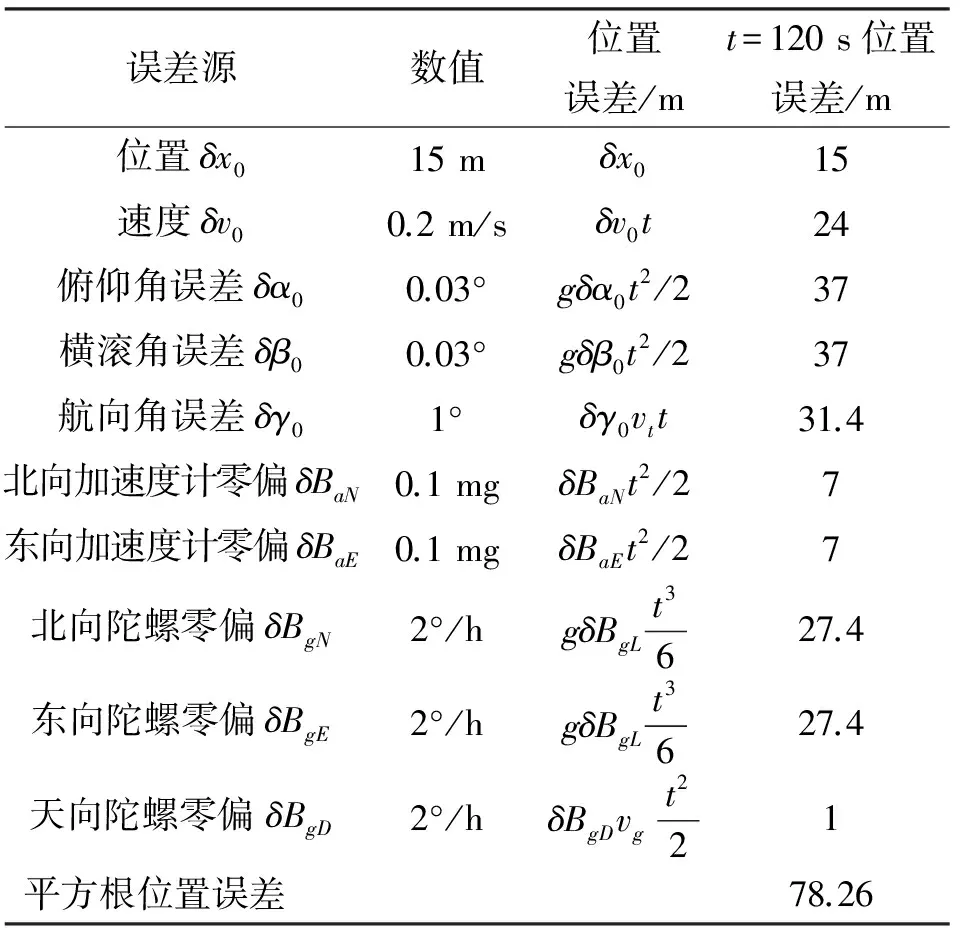
表2 SINS 120 s位置误差估算表Table 2 Evalutation of position error in 120 s for SINS

注：at是系统水平向加速度，加速度值约为1 m/s2，vt为载体水平方向速度，约为15 m/s。

根据分析结果进行了大量的跑车试验，表3列出了惯性导航系统从对准结束开始纯惯性导航120 s时的3次跑车实验结果(以GPS数据作参考)。

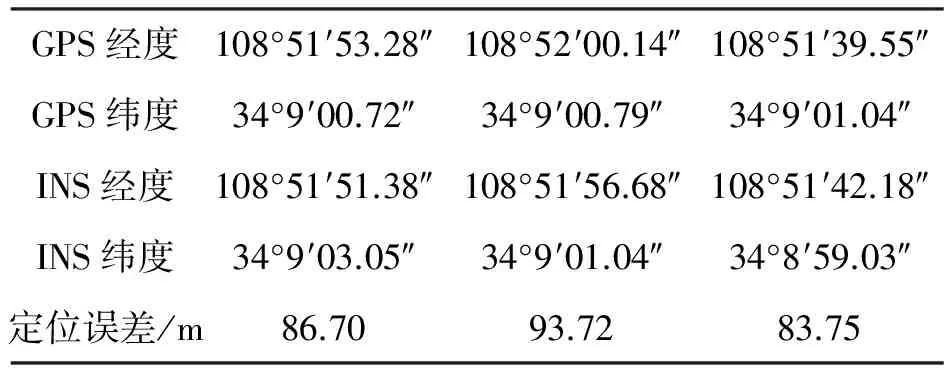
表3 样机跑车试验结果Table 3 Test results of vehicle prototype

表2和表3的结果表明，系统设计方案是完全可行的，这一结果也验证了文中提出的SINS短时工作的工程化误差分析方法的有效性。

4 结束语

本文从对准和导航两个环节分析了引起SINS系统误差的各种因素，并根据SINS工作情况给出了短时工作时的工程化误差传播模型，为SINS的设计及性能分析提供了简洁实用的工程化分析方法。为了分析方便，文中进行了一些条件假设，SINS实际工作时的环境条件远比静止时恶劣，但这并不影响分析结果的可参考性，另外，文中对各种主要误差因素进行了单独分析，实际系统中，这些误差因素往往互相交叉综合产生作用，有可能有一些相互抵消的效果但也有叠加的效果，一般，在设计SINS选择惯性传感器及对其误差因素建模补偿时，应先从静止导航条件入手仔细分析并充分考虑减小每一种不利因素的影响，如：系统对准精度可以通过改进对准算法或采用多位置对准方法提高，陀螺零偏误差、标度因数非线性等都可以在实验室通过前期大量的实验数据进行误差建模并通过误差补偿来消除或减到最小等，SINS的系统误差估算对每个误差源引起的误差求均方根得出。

[1] Titterton D H, Weston J L. Strapdown inertial navigation technology[M]. 2nd ed. America: American Institute of Aeronautics & Astronautics, 2004.

[2] Qin Yongyuan. Inertial navigation[M].Beijing: Science Press,2006.

秦永元.惯性导航[M].北京：科学出版社,2006.

[3] Yan Gongmin,Qin Yongyuan,Wei Yuxin,et al.New initial alignment algorithm for SINS on moving base[J].Systems Engineering and Electronics, 2009，31(3):634-637.

严恭敏，秦永元，卫育新，等.一种适用于SINS动基座初始对准的新算法[J].系统工程与电子技术，2009，31(3):634-637.

[4] Wu Feng,Qin Yongyuan,Cheng Yan.Transfer alignment for missile-born SINS using airborne GPS on moving base[J].Journal of Chinese Inertial Technology, 2013，21(1):56-60.

吴枫，秦永元，成研.基于GPS的弹载捷联惯导动基座传递对准技术[J]. 中国惯性技术学报，2013，21(1):56-60.

[5] Kang Zhen,Guo Shuanyun,Ma Zhongxiao,et al.Adaptive filtering method fo QMEMS gyro[J]. Journal of Applied Optics, 2011, 32(3)：526-529.

康臻，郭栓运，马忠孝，等. 基于QMEMS陀螺的自适应滤波方法研究[J]. 应用光学，2011，32(3)：526-529.

[6] Long Xingwu,Yu Xudong,Zhang Pengfei,et al. Single-rotation inertial navigation system with ring laser gyroscope[J]. Journal of Chinese Inertial Technology, 2011，18(2):149-153.

龙兴武，于旭东，张鹏飞，等. 激光陀螺单轴旋转惯性导航系统[J]. 中国惯性技术学报，2011，18(2):149-153.

[7] Weng Haina,Yao Qi,Hu Xiaomao. Dynamic initial alignment for single-axis rotation laser gyro SINS on board ship[J]. Journal of Chinese Inertial Technology, 2012，20(1):34-38.

翁海娜，姚琪，胡小毛. 舰船单轴旋转激光捷联惯导系统动态初始对准[J]. 中国惯性技术学报，2012，20(1):34-38.

[8] Zhang Zhixin,Xia Jinqiao,Cai Chunlong.Engineering realization of calibrating FOG’s scale factor in segments[J]. Journal of Chinese Inertial Technology, 2008，16(1):99-103.

张志鑫，夏金桥，蔡春龙. 光纤陀螺标定因数分段标定的工程实现[J]. 中国惯性技术学报，2008，16(1):99-103.

[9] Zhang Xiaoyue,Yang Gongliu,Zhang Chunxi. High precision calibration method for three-cluster FOG[J].Journal of Beijing University of Aeronautics and Astronautics, 2012，38(4):478-486.

张晓跃，杨公流，张春熹. 三轴一体光纤陀螺高精度标定方法[J]. 北京航空航天大学学报，2012，38(4):478-486.

[10] Lu Junjie,Zhou Jun, Liu Xiaodong, et al. The measurement correction of MEMS gyroscope based interlaced Kalman filtering[J]. Advanced Materials Research,2011, 301-303:1083-1088.